Похожие презентации:
Колебания и волны
1.
2.
Колебания- процессы, повторяющиеся во
времени, их тип определяет природа
процесса;
механические, электромагнитные,
электромеханические и другие.
Периодические - повторяются через
равные промежутки времени.
Гармонические - описываются законом
синуса или косинуса.
3.
Механические колебанияМТ
xm
x
0
xm
x
X 0
x xm sin t 0
0 0
t
- координата (смещение) МТ
в момент времени t;
xm - максимальное смещение
(амплитуда колебаний);
- циклическая частота; t 0 - фаза;
0 - начальная фаза колебаний.
4.
Электромагнитные колебанияпроисходят
в колебательном
контуре;
по гармоническому закону изменяются: заряд и разность потенциалов обкладок конденсатора, сила
тока в цепи, напряженность электрического поля конденсатора, индукция магнитного поля катушки.
5.
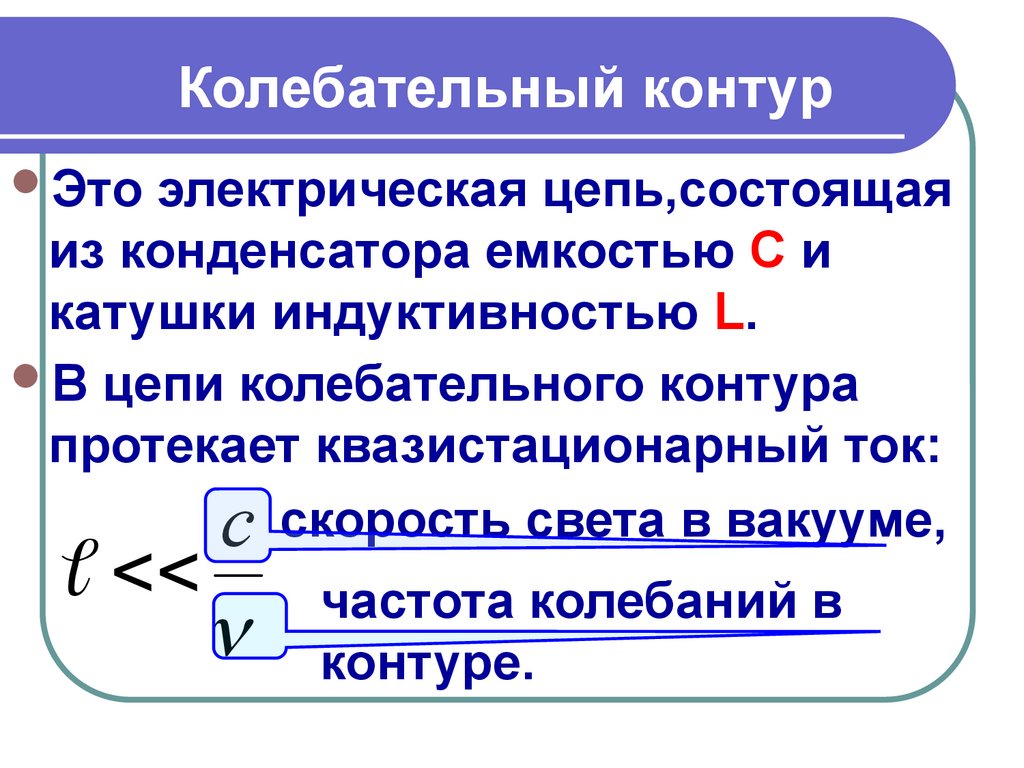
Колебательный контурЭто
электрическая цепь,состоящая
из конденсатора емкостью С и
катушки индуктивностью L.
В цепи колебательного контура
протекает квазистационарный ток:
c скорость света в вакууме,
частота колебаний в
контуре.
6.
Свободные колебанияЗакон Ома для участка 1-R-L-2:
IR 1 2 c ;
dQ
Q
dI
1 2 ; c L ; I
;
C
dt
dt
2
R
dI d Q
Q
2 ;
1
C
dt
L dt
Q
2
I 0
2
d Q R dQ Q
0
2
dt
L dt LC
7.
Незатухающие свободные колебания2
R 0 d Q
1
Q
0
;
2
LC
dt
2
d Q
2
2
Q
0
0
0
2
dt
Q Qm sin( 0t 0 );
1
0
; T 2 2 LC .
0
LC
0
8.
Затухающие свободные колебанияЭнергия
реальной колебательной системы с течением времени уменьшается.
Параметры линейной системы в ходе
процесса не изменяются.
Период затухающих колебаний – время,
в течение которого система дважды
проходит положение равновесия в
одном и том же направлении.
9.
Уравнение затухающих колебанийR 0
2
d Q
R dQ 1
Q
0
;
2
L dt LC
dt
2
d Q
dQ
2
2
Q
0
;
0
2
dt
dt
Q Qm e
t
cos( t 0 );
2
2
2
2
.
0 ; T
2
2
0
10.
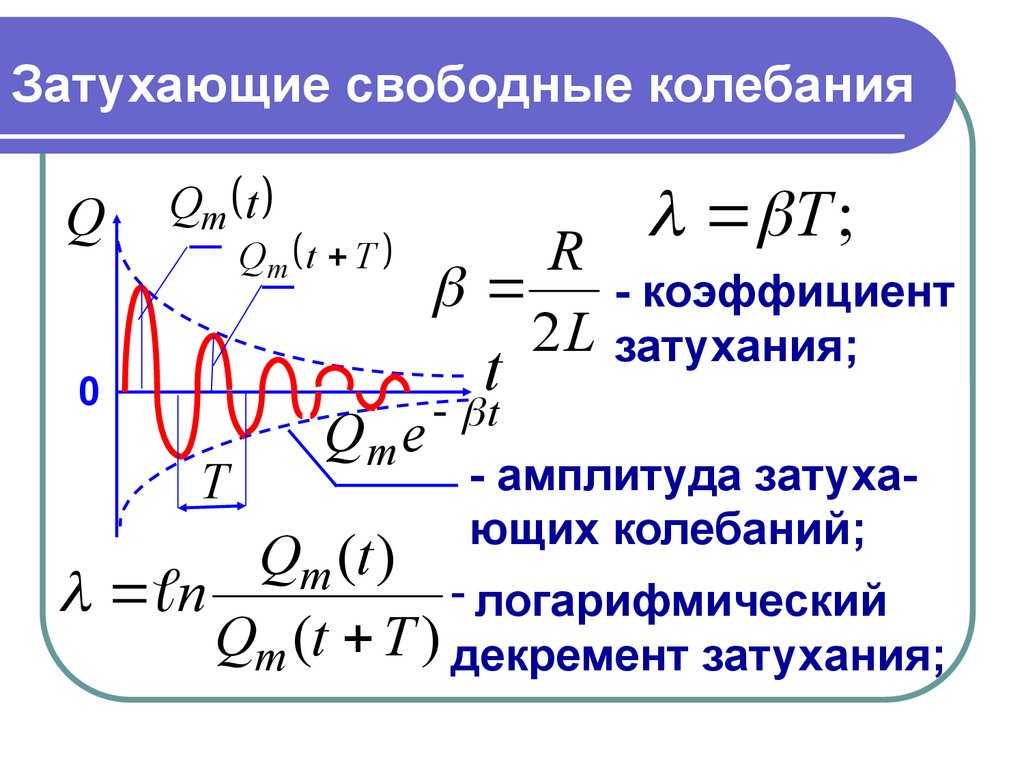
Затухающие свободные колебанияQ
Qm t
Qm t T
0
Т
Qm e
t
Т ;
R
2L
- коэффициент
затухания;
t
- амплитуда затухающих колебаний;
Qm (t )
- логарифмический
n
Qm (t T ) декремент затухания;
11.
Вынужденные колебанияДля получения незатухающих колебаний в контур включают источник переменной ЭДС.
Q
dI
R
-Q
C
I >0
L
Q
2
IR
C
L
dt
(t );
( t ) m cos t ;
m
d Q
dQ
2
2
0 Q cos t
2
dt
dt
L
12.
Q Q m cos( t 0 )- решение неоднородного уравнения
Qm
Q Qm cos( t 0 )
2
m
R L 1 /( C )
2
- амплитуда
R
tg 0
- начальная фаза
L 1 /( C )
установившихся вынужденных
колебаний.
13.
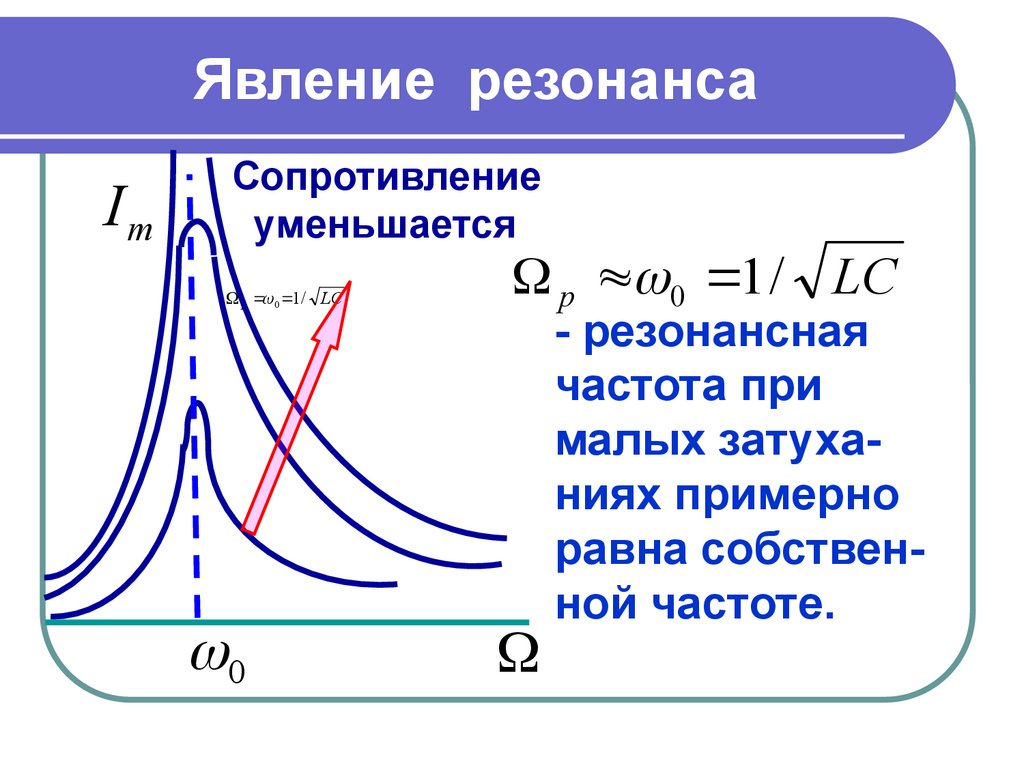
Явление резонансаIm
Cопротивление
уменьшается
р 0 1 / LC
0
р 0 1 / LC
- резонансная
частота при
малых затуханиях примерно
равна собственной частоте.
14.
СЛОЖЕНИЕ КОЛЕБАНИЙСложить
колебания – определить
закон результирующего колебания
системы.
Сложение одинаково направленных гармонических колебаний.
Сложение взаимно перпендикулярных гармонических колебаний.
15.
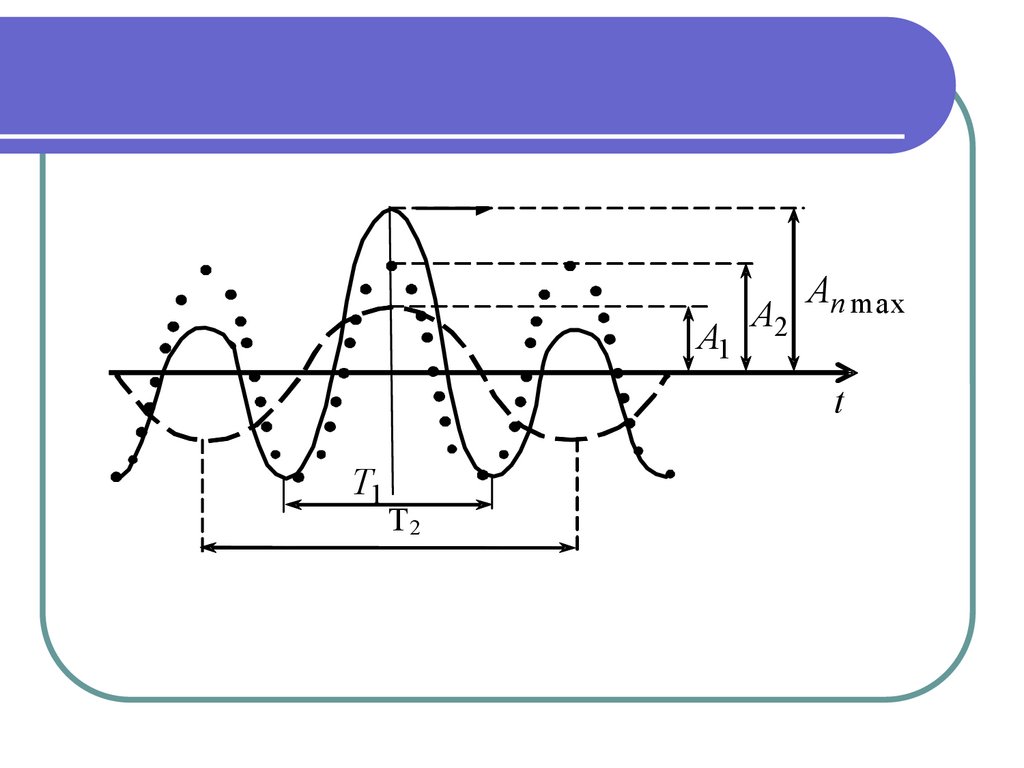
1) Колебания одногонаправления: 1 2 ; 01
02 .
s1 A1 sin( 1t 01 )
+
s2 A2 sin( 2t 02 )
s A sin
- результирующее колебание
является гармоническим.
16.
А1А2
Аn max
t
T1
T2
17.
МЕТОД ВЕКТОРНЫХ ДИАГРАММ2 1 ( 2 1 )t ( 02 01)
Y
A2
O 2 1
разность
фаз
гармоA
нических колебаний;
A1 sin 1 A2 sin 2
tg
A1
A1 cos 1 A2 cos 2
-определяет фазу резульX тирующего колебания ;
A ( t ) A12 A 22 2 A1 A 2 cos( 2 1 )
-амплитуда результирующего колебания.
18.
КОГЕРЕНТНЫЕ КОЛЕБАНИЯГармонические
колебания когерентны
(согласованы), если разность фаз этих
колебаний со временем не изменяется.
Когерентны гармонические колебания с
равными циклическими частотами:
2 m - колебания в одной фазе;
2
1
( 2m 1) - колебания в
2
1
противофазе.
m = 0, 1, 2,… - целое число.
19.
2) Колебания взаимно 1 2перпендикулярны: 01 02 0
+
A1
Y ctg A
2
x A1 sin t
y A2 sin t
A1
x y
A2
A2
A1
A2
A1
X
Результирующее колебание – гармоническое с
частотой
и амплитудой A А12 А22 .
Это линейно поляризованные колебания.
20.
2) Колебания взаимно 1 2 ;перпендикулярны: 01 2 ; 02 0
x A1 sin( t ) A1 cos t
2
+
Y
y A 2 sin t
2
2
x
y
2 1
2
A1
A2
A2
A1
x
Эллиптически поляризованные колебания.
При равенстве амплитуд слагаемых колебаний – поляризованные по кругу.
21.
ФИГУРЫ ЛИССАЖУЭто траектории, прочерчиваемые
точкой, участвующей во взаимно
перпендикулярных колебаниях.
Вид траектории зависит от соотношения амплитуд, частоты, разности фаз слагаемых колебаний.
По виду фигуры Лиссажу можно
определить соотношение частот
слагаемых колебаний.
22.
Волны в упругой средеУпругие
или механические волны –
это распространяющиеся в упругой среде деформации.
Звуковые волны – упругие волны
малой интенсивности.
Волны
с частотой от 16 Гц до 20 кГц –
слышимые звуки; меньше 16 Гц –
инфразвук; больше 20кГц – ультразвук;
свыше 1 ГГц – гиперзвук.
23.
ТИПЫ УПРУГИХ ВОЛНПродольная
упругая волна – частицы среды колеблются в направлении распространения волны (газ,
жидкость, твердое тело).
Поперечная упругая волна – частицы среды колеблются в направлении перпендикулярном распространению волны ( твердое тело).
24.
Волна «бежит» вдоль ОХυ
Y
А
В
О
х
X
25.
Этораспространяющееся в пространстве переменное электромагнитное
поле.
Гипотеза о существовании электромагнитных волн высказана Максвеллом:
с 1 / 0 0
-скорость распространения электромагнитных волн в вакууме.
26.
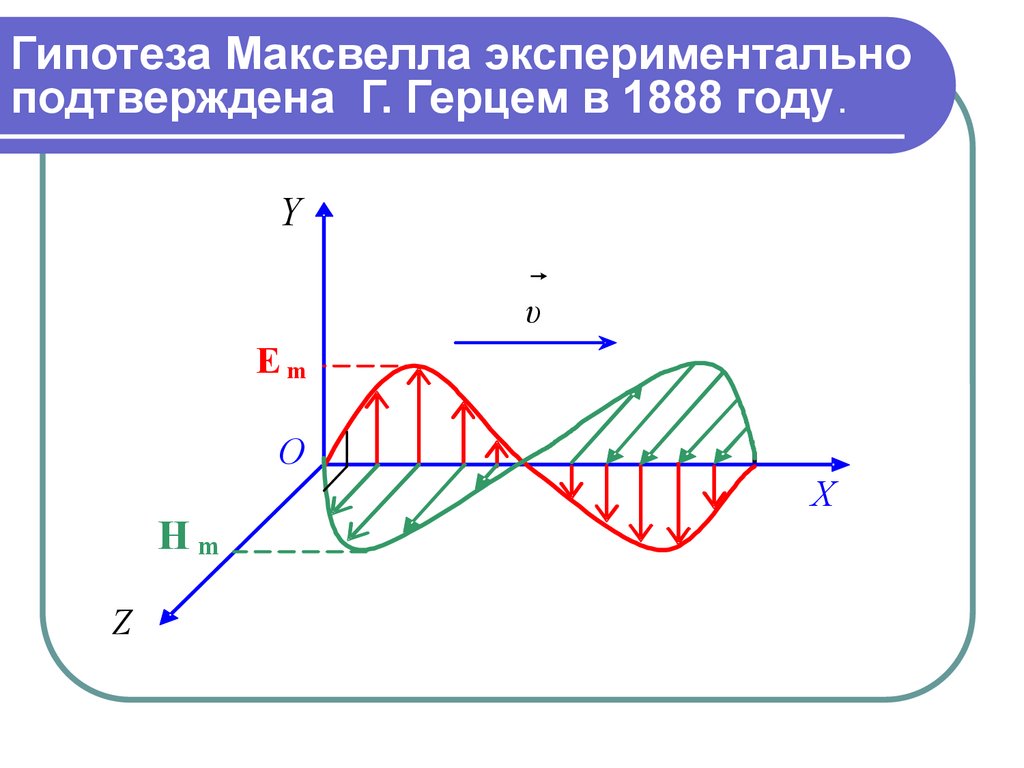
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ- поперечные,, векторы Е и Н
изменяются во взаимно перпендикулярных плоскостях,
образуют правую тройку;
их модули связаны соотношением
0
H
E.
0
27.
Уравнение электромагнитнойволны
Плоская электромагнитная волна
распространяется в положительном направлении оси ОХ
x
x
E E m cos (t ), H H m cos (t );
амплитуды волны;
2
;
- волновое число, k
с / - фазовая скорость.
k
28.
Уравнение плоскойэлектромагнитной волны
с учетом принятых обозначений
E E m cos( t kx ),
H H m cos( t kx ).
29.
Гипотеза Максвелла экспериментальноподтверждена Г. Герцем в 1888 году.
Y
υ
Еm
О
Hm
Z
Х
30.
Энергия электромагнитнойволны
Объемная
плотность энергии
электромагнитной волны
1
2 1
2
2
2
w 0 E 0 H 0 E 0 H .
2
2
Интенсивность монохроматической
бегущей электромагнитной волны
1 0 2 А – амплитуда
колебаI
A ,
ний вектора E .
2 0
























 Физика
Физика








