Похожие презентации:
Прямые частного положения. Теорема Фалеса. Деление отрезка на равные части. Тема №3
1. Тема №3. Прямые частного положения. Теорема Фалеса. Деление отрезка на равные части.
2.
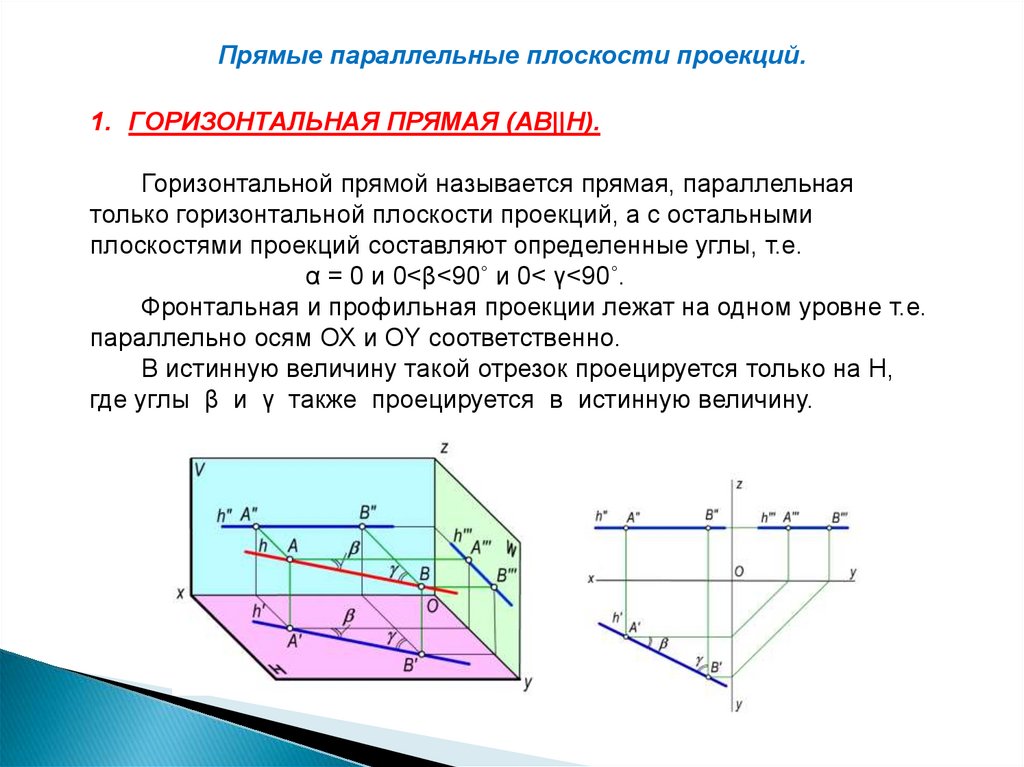
Прямые параллельные плоскости проекций.1. ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ (АВ||Н).
Горизонтальной прямой называется прямая, параллельная
только горизонтальной плоскости проекций, а с остальными
плоскостями проекций составляют определенные углы, т.е.
α = 0 и 0<β<90˚ и 0< γ<90˚.
Фронтальная и профильная проекции лежат на одном уровне т.е.
параллельно осям ОХ и ОY соответственно.
В истинную величину такой отрезок проецируется только на Н,
где углы β и γ также проецируется в истинную величину.
3.
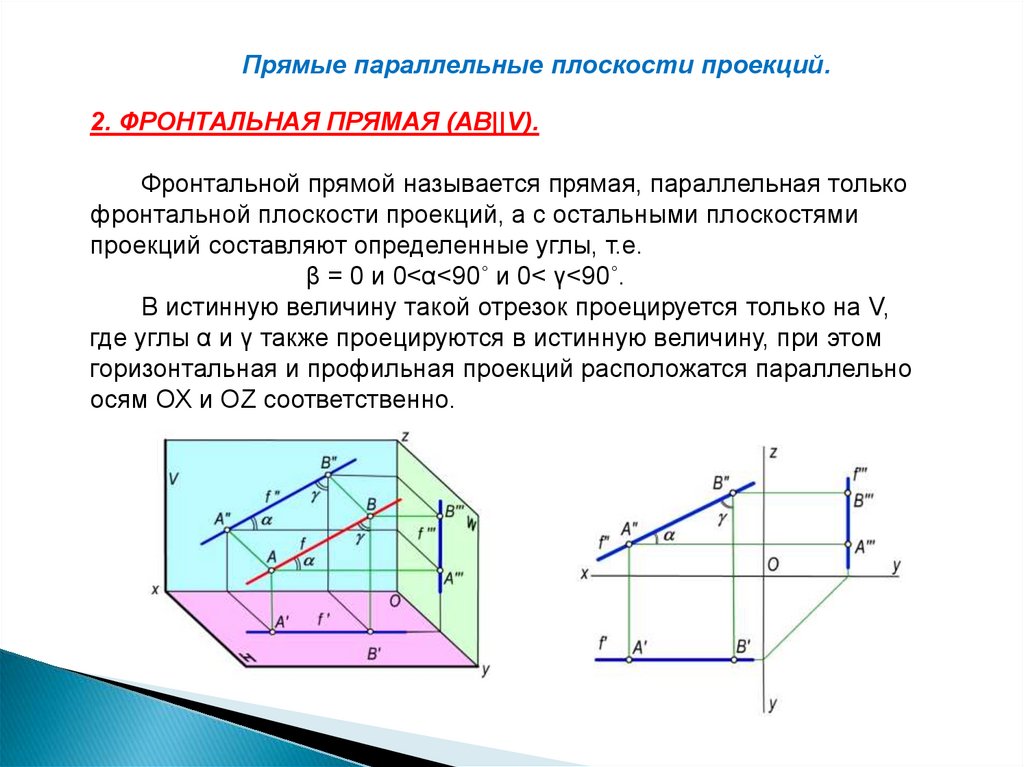
Прямые параллельные плоскости проекций.2. ФРОНТАЛЬНАЯ ПРЯМАЯ (АВ||V).
Фронтальной прямой называется прямая, параллельная только
фронтальной плоскости проекций, а с остальными плоскостями
проекций составляют определенные углы, т.е.
β = 0 и 0<α<90˚ и 0< γ<90˚.
В истинную величину такой отрезок проецируется только на V,
где углы α и γ также проецируются в истинную величину, при этом
горизонтальная и профильная проекций расположатся параллельно
осям ОХ и ОZ соответственно.
4.
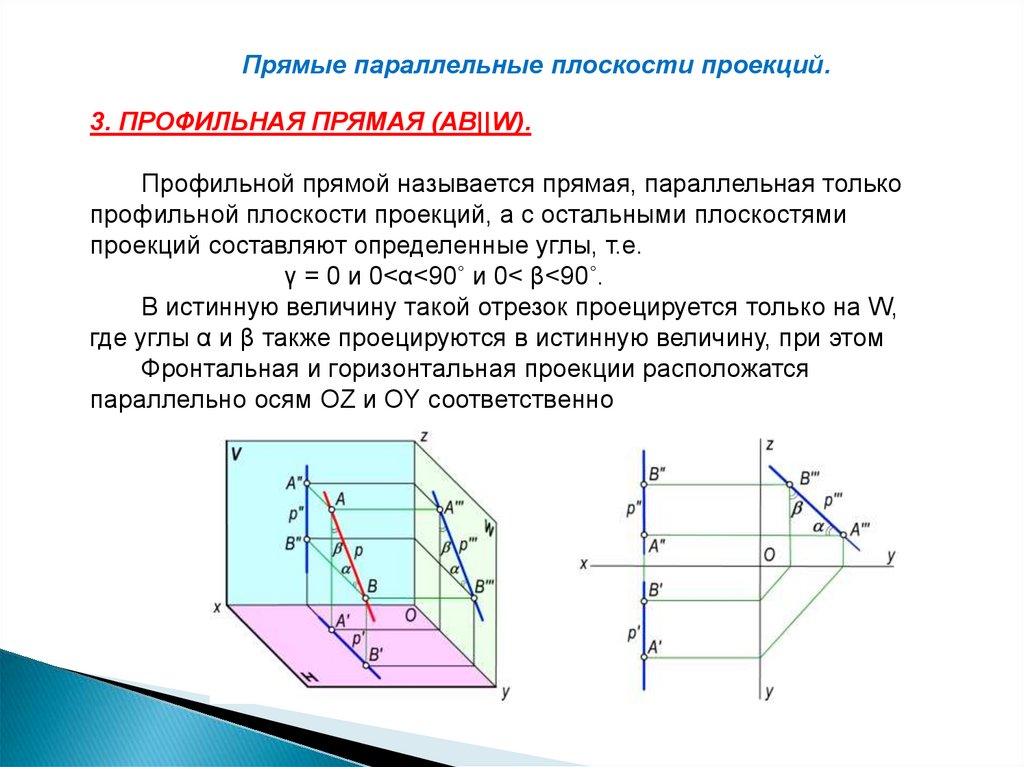
Прямые параллельные плоскости проекций.3. ПРОФИЛЬНАЯ ПРЯМАЯ (АВ||W).
Профильной прямой называется прямая, параллельная только
профильной плоскости проекций, а с остальными плоскостями
проекций составляют определенные углы, т.е.
γ = 0 и 0<α<90˚ и 0< β<90˚.
В истинную величину такой отрезок проецируется только на W,
где углы α и β также проецируются в истинную величину, при этом
Фронтальная и горизонтальная проекции расположатся
параллельно осям ОZ и ОY соответственно
5.
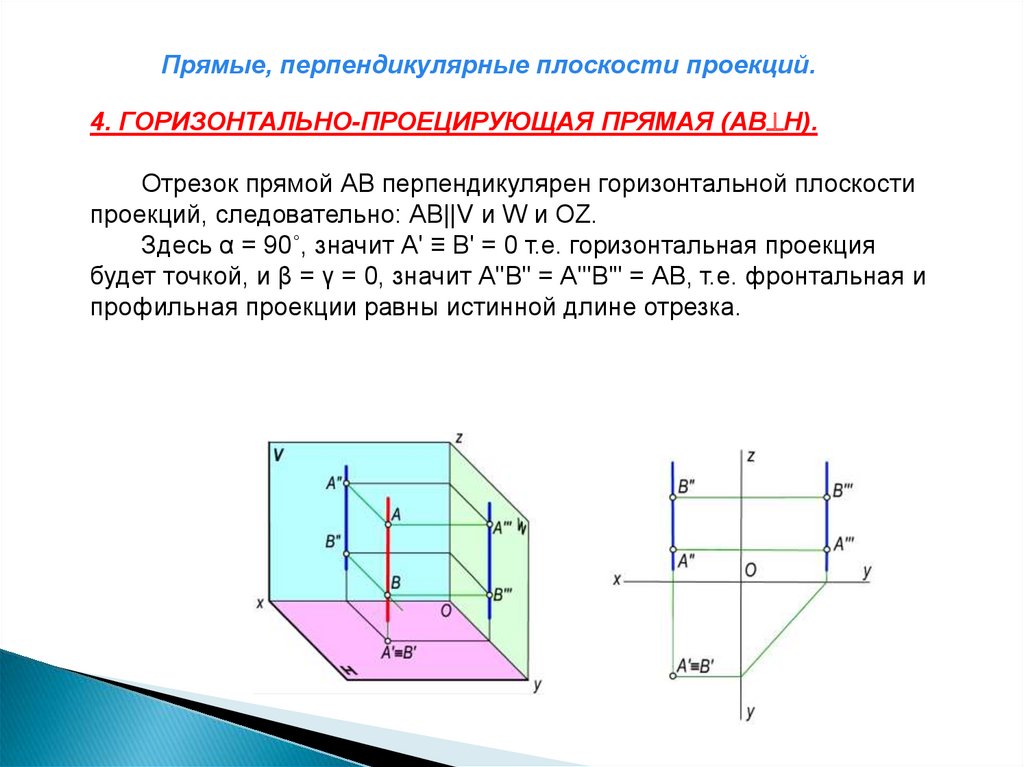
Прямые, перпендикулярные плоскости проекций.4. ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ (АВ Н).
Отрезок прямой АВ перпендикулярен горизонтальной плоскости
проекций, следовательно: АВ||V и W и ОZ.
Здесь α = 90˚, значит А' ≡ В' = 0 т.е. горизонтальная проекция
будет точкой, и β = γ = 0, значит А"В" = А'"В'" = АВ, т.е. фронтальная и
профильная проекции равны истинной длине отрезка.
6.
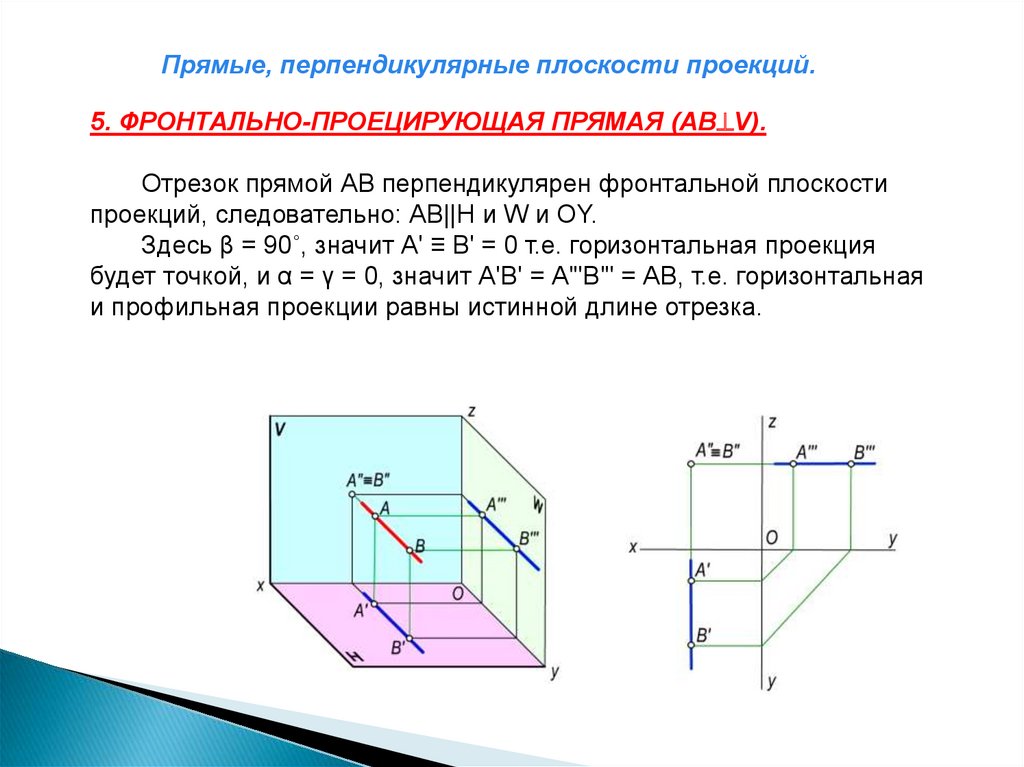
Прямые, перпендикулярные плоскости проекций.5. ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ (АВ V).
Отрезок прямой АВ перпендикулярен фронтальной плоскости
проекций, следовательно: АВ||Н и W и ОY.
Здесь β = 90˚, значит А' ≡ В' = 0 т.е. горизонтальная проекция
будет точкой, и α = γ = 0, значит А'В' = А'"В'" = АВ, т.е. горизонтальная
и профильная проекции равны истинной длине отрезка.
7.
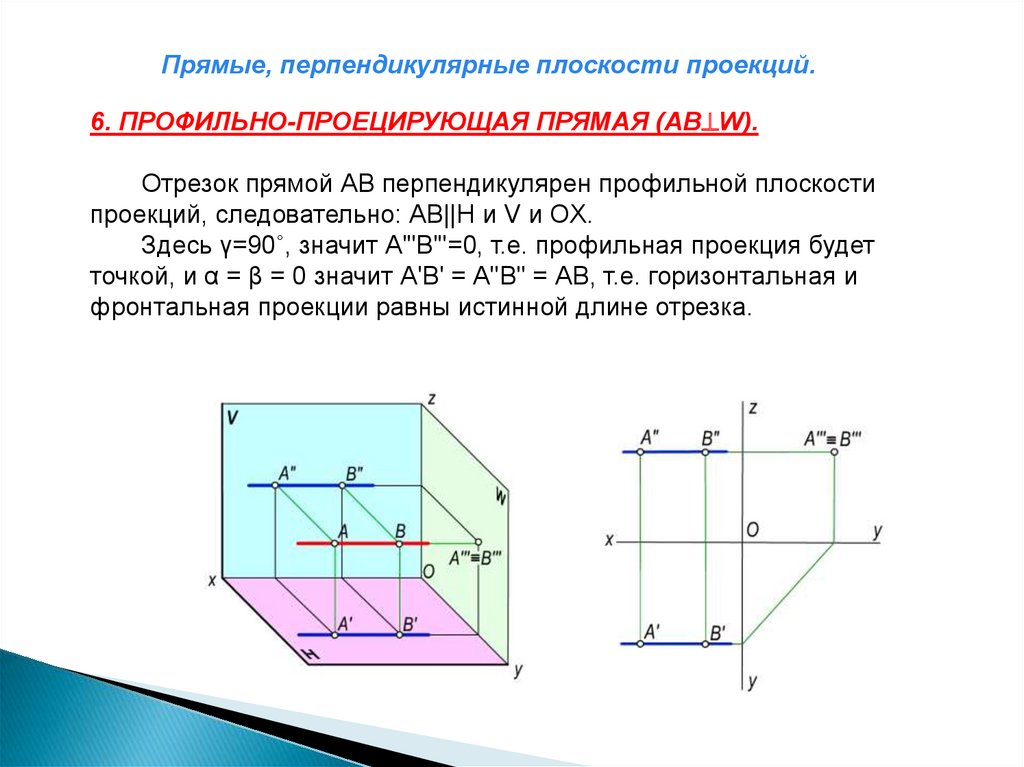
Прямые, перпендикулярные плоскости проекций.6. ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ (АВ W).
Отрезок прямой АВ перпендикулярен профильной плоскости
проекций, следовательно: АВ||Н и V и ОX.
Здесь γ=90˚, значит А'"В'"=0, т.е. профильная проекция будет
точкой, и α = β = 0 значит А'В' = А"В" = АВ, т.е. горизонтальная и
фронтальная проекции равны истинной длине отрезка.
8.
ДЕЛЕНИЕ ОТРЕЗКА В ЗАДАННОМОТНОШЕНИИ
Если необходимо разделить отрезок
прямой на две части, в заданном отношении, то
надо разделить в этом же отношении его
проекции.
Пример: требуется разделить заданный отрезок
АВ на две части, в данном отношении m:n. Это
значит, что требуется найти внутри АВ точку К так,
чтобы АК:КВ = m:n или КВ:КА = m:n.
9.
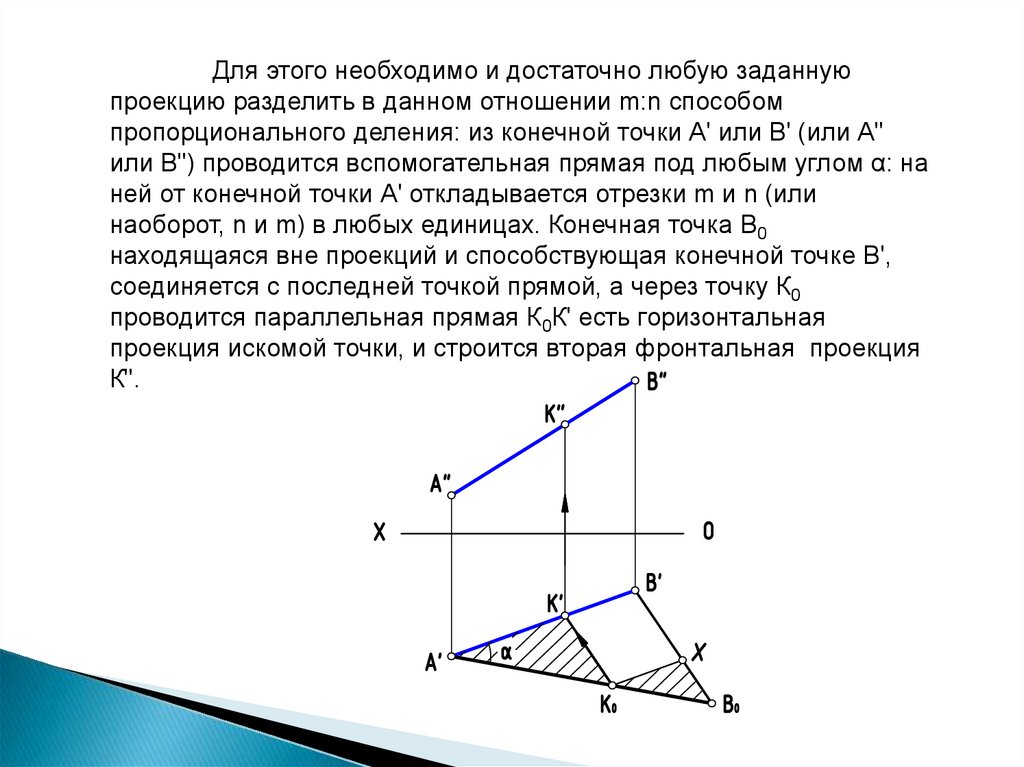
Для этого необходимо и достаточно любую заданнуюпроекцию разделить в данном отношении m:n способом
пропорционального деления: из конечной точки А' или В' (или А"
или В") проводится вспомогательная прямая под любым углом α: на
ней от конечной точки А' откладывается отрезки m и n (или
наоборот, n и m) в любых единицах. Конечная точка В0
находящаяся вне проекций и способствующая конечной точке В',
соединяется с последней точкой прямой, а через точку К0
проводится параллельная прямая К0К' есть горизонтальная
проекция искомой точки, и строится вторая фронтальная проекция
К".


 Инженерная графика
Инженерная графика








