Похожие презентации:
«Выпуклость и точки перегиба графика функции. Асимптоты». Лекция № 3
1.
2.
1. Выпуклость графика функции. Достаточноеусловие
выпуклости графика функции .
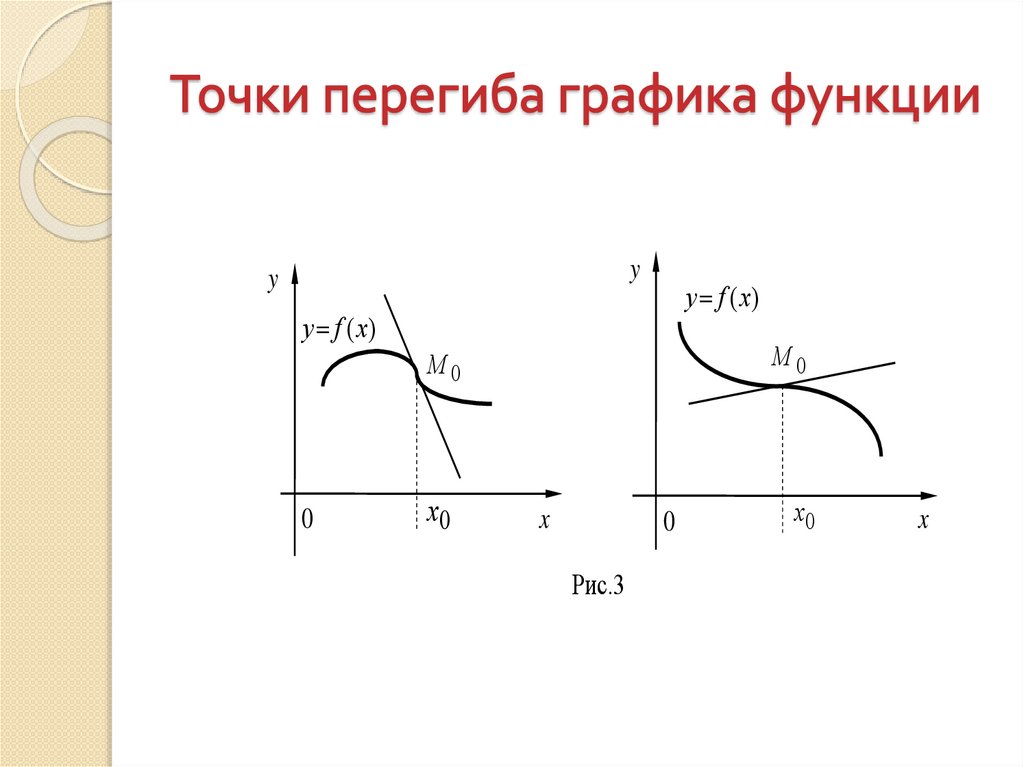
2. Точки
перегиба
графика
функции.
Необходимое и
достаточное условия
точки перегиба графика функции .
3. Асимптоты графика функции .
3.
Введение понятий выпуклой кривой, точкиперегиба кривой, критической точки функции по
второй
производной,
асимптот
кривой.
Рассмотрение достаточного условия выпуклости
кривой, необходимого и достаточного условий
существования точки перегиба, необходимого и
достаточного
условий
существования
невертикальной асимптоты.
4.
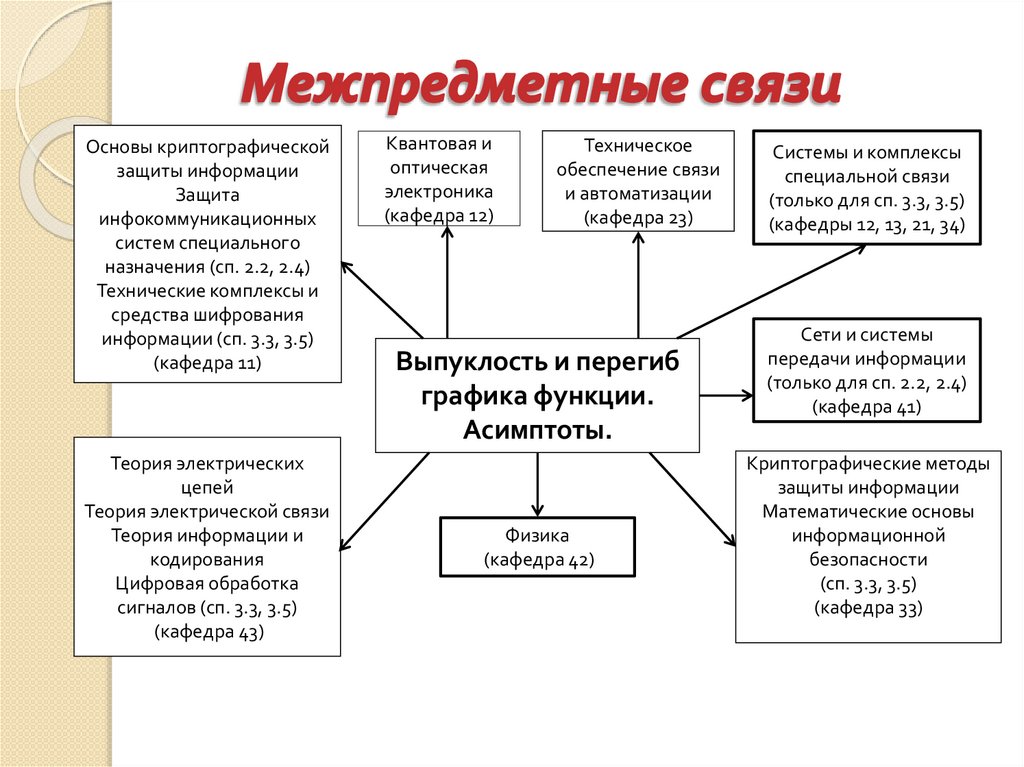
Основы криптографическойзащиты информации
Защита
инфокоммуникационных
систем специального
назначения (сп. 2.2, 2.4)
Технические комплексы и
средства шифрования
информации (сп. 3.3, 3.5)
(кафедра 11)
Теория электрических
цепей
Теория электрической связи
Теория информации и
кодирования
Цифровая обработка
сигналов (сп. 3.3, 3.5)
(кафедра 43)
Квантовая и
оптическая
электроника
(кафедра 12)
Техническое
обеспечение связи
и автоматизации
(кафедра 23)
Выпуклость и перегиб
графика функции.
Асимптоты.
Физика
(кафедра 42)
Системы и комплексы
специальной связи
(только для сп. 3.3, 3.5)
(кафедры 12, 13, 21, 34)
Сети и системы
передачи информации
(только для сп. 2.2, 2.4)
(кафедра 41)
Криптографические методы
защиты информации
Математические основы
информационной
безопасности
(сп. 3.3, 3.5)
(кафедра 33)
5.
yf ( a)
1
2
f( a )
1
2 e
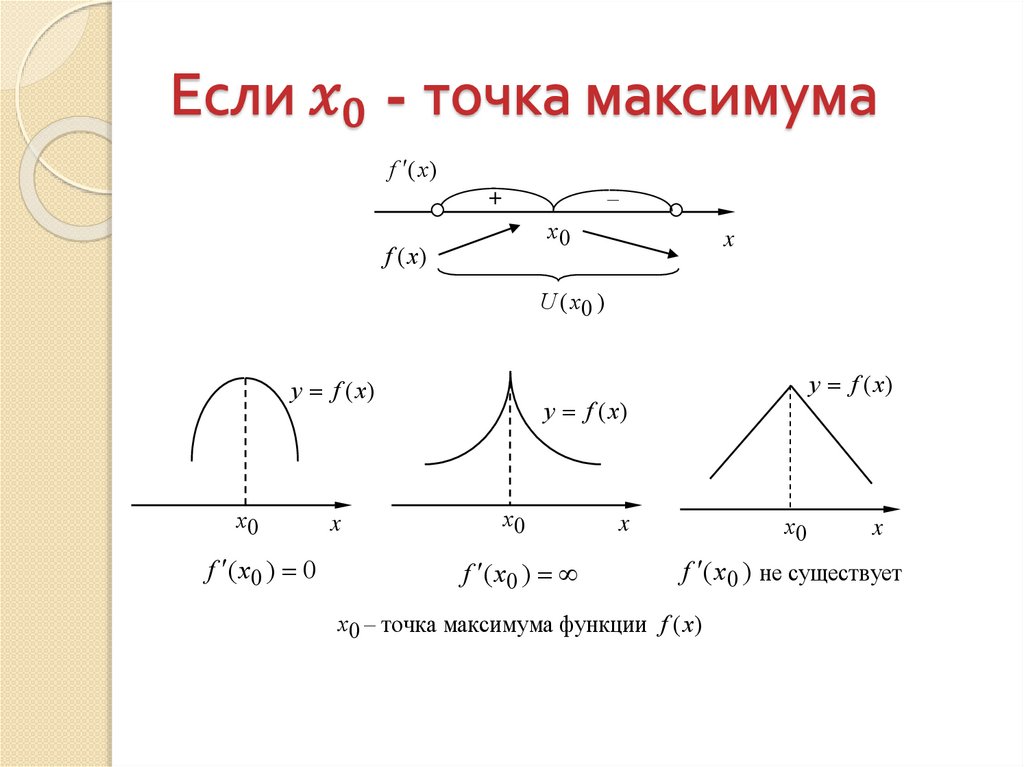
6.
f (x )–
+
x0
f (x)
x
U (x 0 )
y f (x)
x0
f ( x0 ) 0
x
y f (x)
y f (x)
x0
f ( x0 )
x0
x
x
f ( x0 ) не существует
x 0 – точка максимума функции f (x)
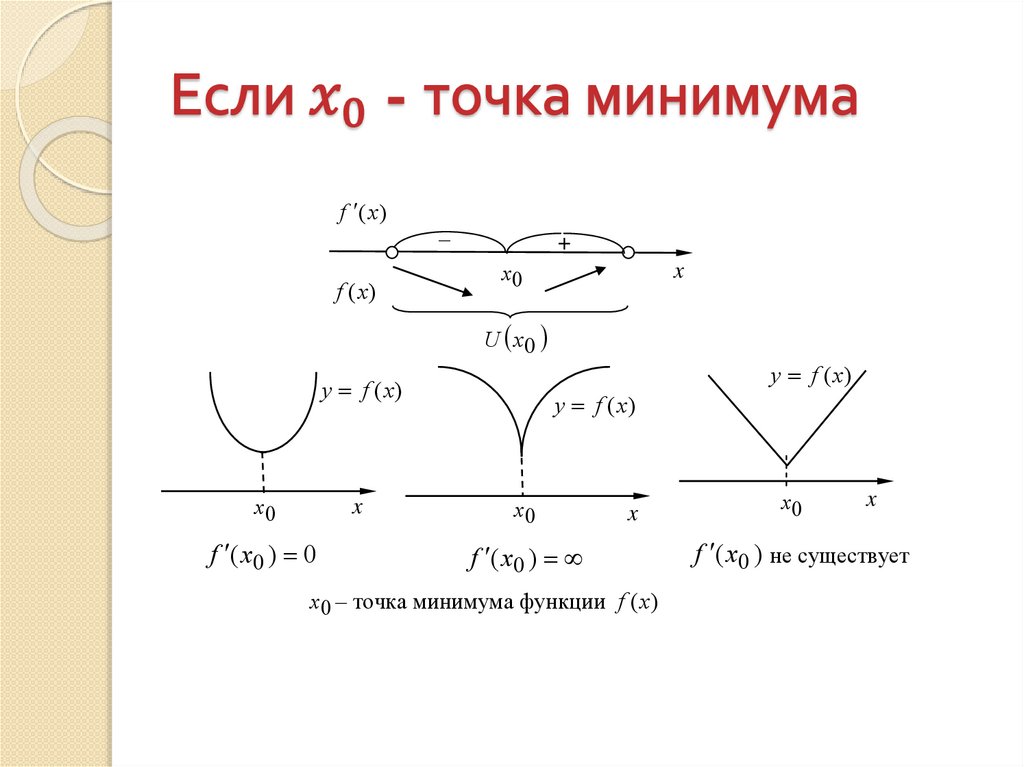
7.
f (x )–
f (x)
+
x0
x
U x0
y f (x)
y f (x)
x0
x
f ( x0 ) 0
y f (x)
x0
x
f ( x0 )
x 0 – точка минимума функции f (x)
x0
x
f ( x0 ) не существует
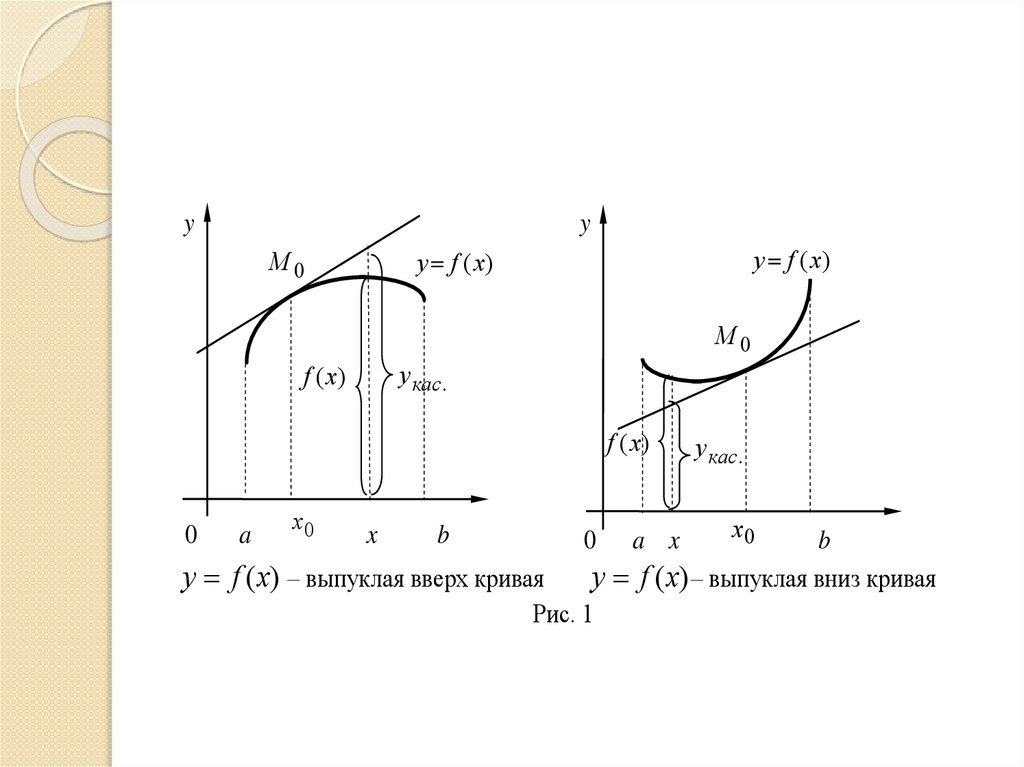
8.
yy
M0
y f (x)
y f (x)
M0
y кас .
f (x)
f (x)
0
x
a
x0
x
b
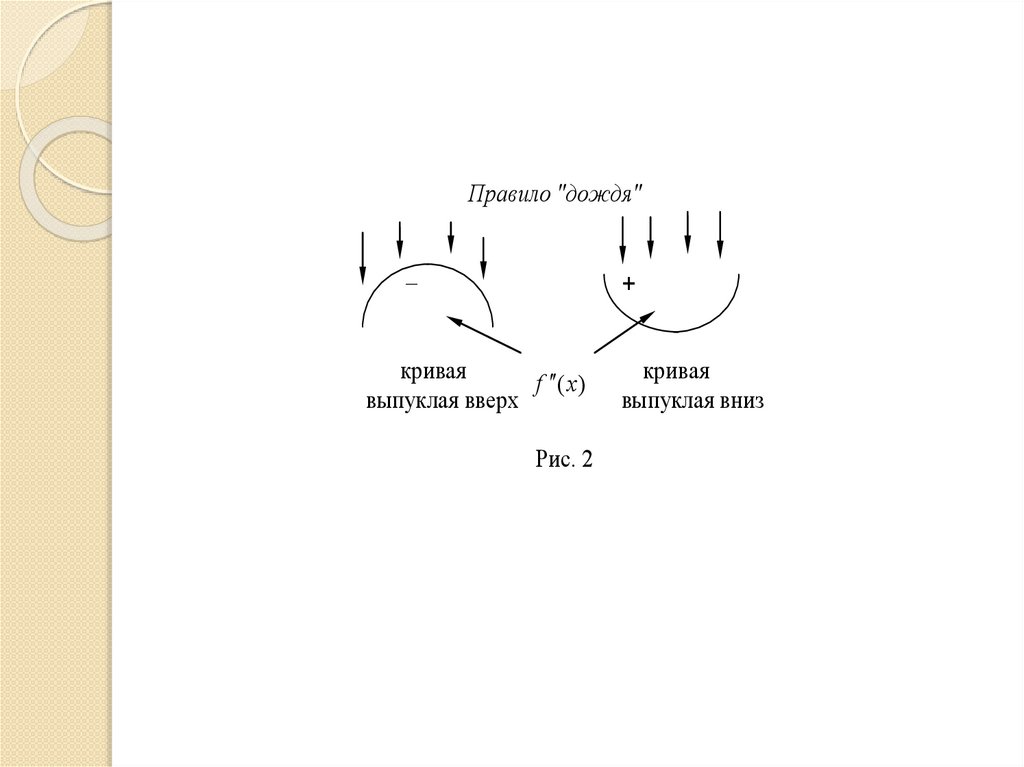
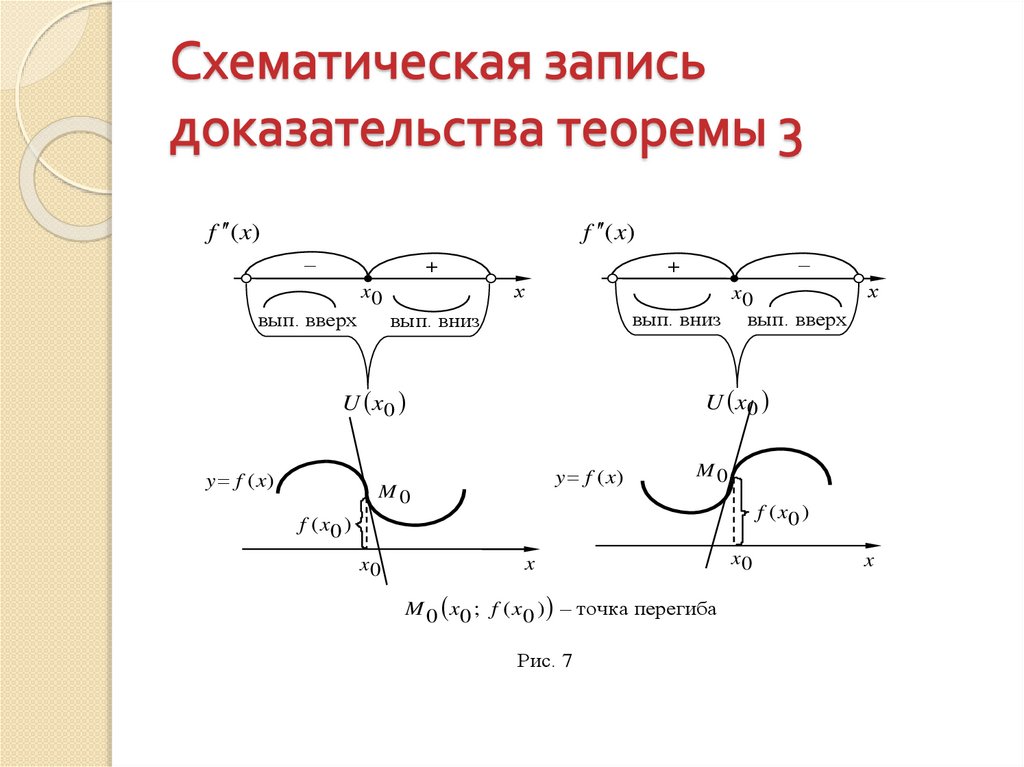
y f (x) – выпуклая вверх кривая
y кас .
x0
0 a x
b
x y f (x) – выпуклая вниз кривая
Рис. 1








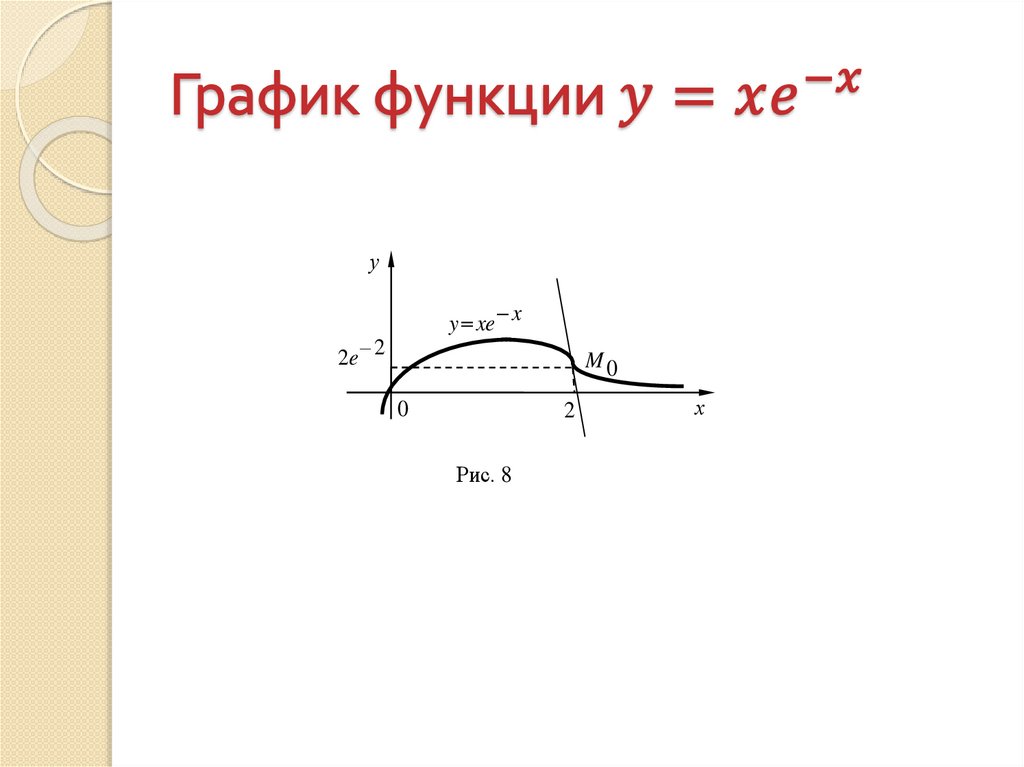
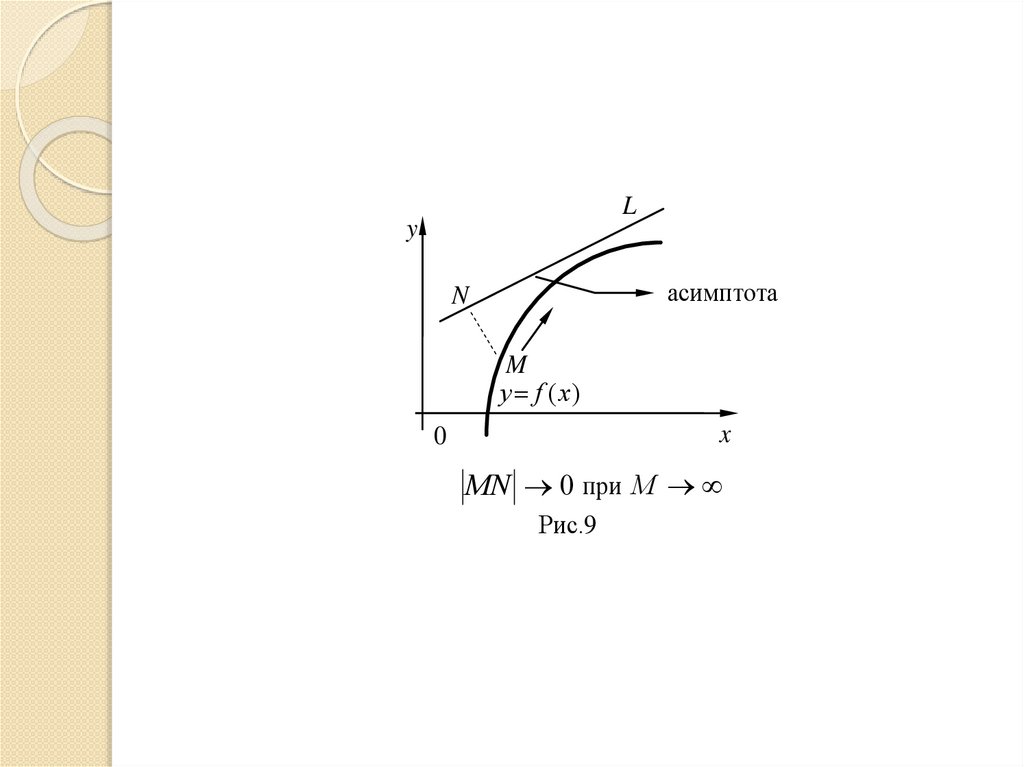



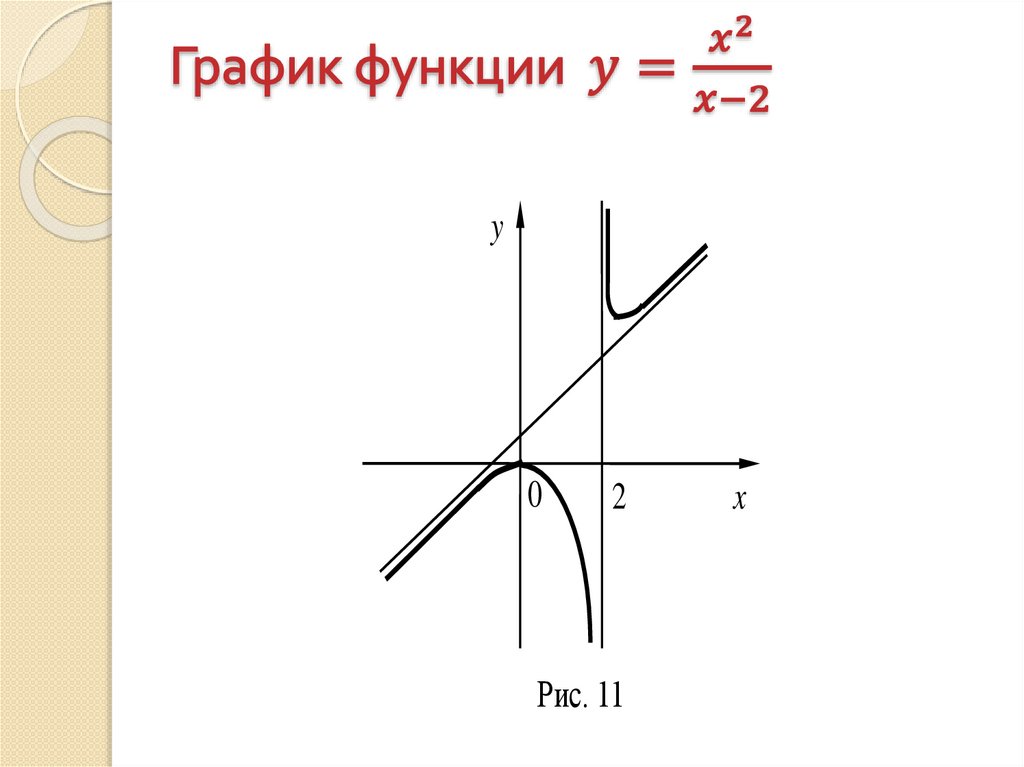

 Математика
Математика








