Похожие презентации:
Производная функции
1.
2.
Понятие касательнойОпределение: Касательной к данной непрерывной кривой в
данной ее точке М (точка касания)
называется предельное положение секущей
ММ', проходящей через точку М, когда
вторая точка пересечения М' неограниченно
приближается по кривой к первой.
Рис. 1
3.
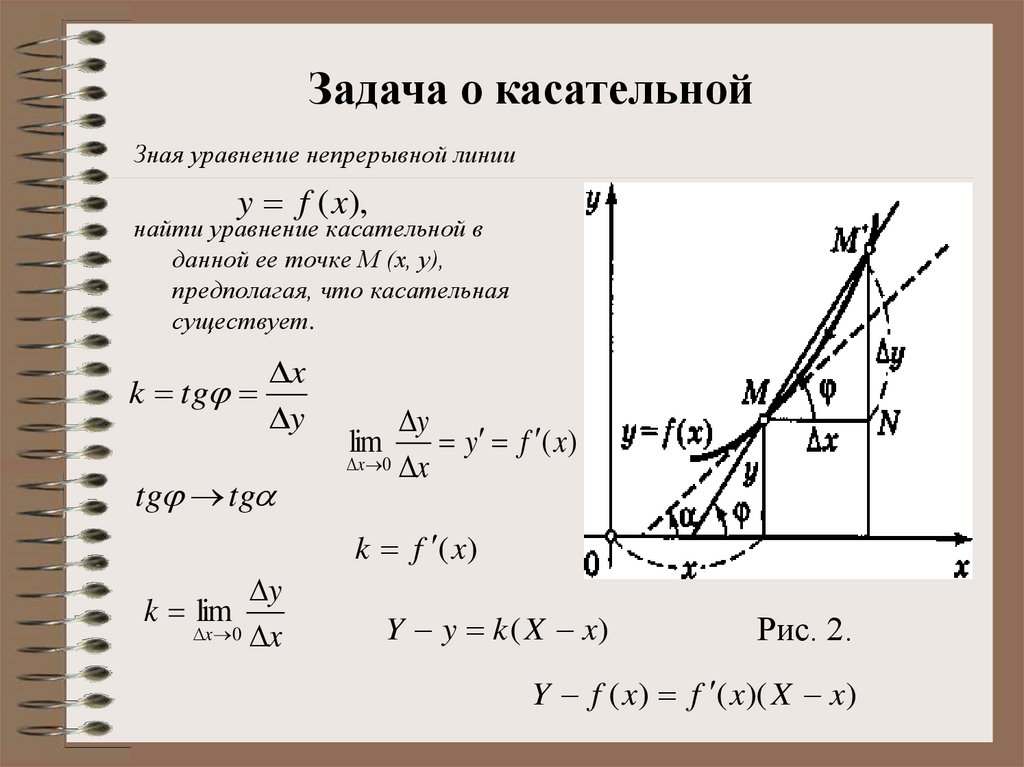
Задача о касательнойЗная уравнение непрерывной линии
y f (x),
найти уравнение касательной в
данной ее точке М (х, у),
предполагая, что касательная
существует.
k tg
x
y
tg tg
y
lim
y f ( x)
x 0 x
k f (x)
y
k lim
x 0 x
Y y k ( X x)
Рис. 2.
Y f ( x) f ( x)( X x)
4.
Задача о скорости движения• Задача. Зная закон движения S=f(t), найти скорость движущейся
точки для любого момента времени.
ОМ = х
t t
OM x x
x x f t
x f (t t ) f (t )
x f (t t ) f (t )
y
t
y
V lim
t 0 t
v f (t )
5.
Общее определение производнойОпределение: Производной функции у = f(х)
называется предел отношения
приращения функции к
приращению аргумента при
условии, что приращение
аргумента стремится к нулю,
если этот предел существует
y
x 0 x
y f ( x) lim
Найти производную функции у = х2
x 0
y = (х + x )2
y lim
x 0
y ( x x) 2 x 2 2 x * x ( x) 2
y
lim
(2 x x) 2 x
x 0
x
(х2)' = 2х
6.
Смысл производнойФизический
Геометрический
Если функция описывает f ( x) k касательной к
какой-либо физический
графику функции y=f (x) в
процесс, то y f (x) есть точке, абсцисса которой
скорость
протекания
равна x.
y
этого процесса.
Например
Точка движется
прямолинейно по закону S t 2
.Найти скорость движения
в момент времени t=3
y=kx+b
Уравнение
касательной к кривой
y x2 1
в точке А(1;2)
k y ( x) ( x2 1) 2 x
k=2*1=2
2=2*1+b
b=0
y=2x
7.
Зависимость между непрерывностьюи дифференцируемостью функции
Мы видели, что функция
y f (x)
называется непрерывной в точке х, если в этой
точке
lim
y 0
x 0
Функция называется дифференцируемой в
точке х, если в этой точке она имеет производную,
т. е. если существует конечный предел:
lim
x 0
y
y
x
8.
Зависимость междунепрерывностью и
дифференцируемостью функции
ТЕОРЕМА:
Если функция дифференцируема
в некоторой точке, то в этой
точке функция непрерывна.
Обратное утверждение неверно:
непрерывная функция может не
иметь производной.
9.
Правила нахожденияпроизводной
1. Если функции u(x) и v(x) имеют в точке х
производные, то их сумма u(x) + v(x) также имеет в
этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С –
данное число, то функция С∙u(x) также имеет в этой
точке производную, причем
(Сu)′ = С∙u′
(постоянное число выносится за знак производной)
10.
Правила нахожденияпроизводной
3. Если функции u(x) и v(x) имеют в точке х
производные, то их произведение u(x) ∙ v(x) также
имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и
1
v(x) ≠ 0, то функция
также имеет в этой точке
v(x)
производную, причем
v′
1′
=– 2
v
v
()
11.
Правила нахожденияпроизводной
5. Если функции u(x) и v(x) имеют в точке х
u(x)
производные и v(x) ≠ 0, то функция
также имеет
v(x)
в этой точке производную, причем
( )
u ′
u′v – uv′
v =
v2
12.
Производная сложнойфункции
(f(g(x)))′ = f′(g(x))∙g′(x)
Примеры:
1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ =
= 3(5x – 3)2 ∙ 5 = 15(5x – 3)2
2. (sin(4x + 8))′ = cos(4x + 8)∙(4x + 8)′ =
= cos(4x + 8)∙4 = 4 cos(4x + 8)
13.
Понятие о производных высших порядковПроизводная f '(х) от
Пример
функции f (х) называется
производной первого порядка
1)Пусть y = sin x
и представляет собой
Тогда имеем последовательно
некоторую новую функцию.
y cos x, y sin x, y cos x, y IV sin x,.....
Может случиться, что эта
3
функция сама имеет
2)Пусть y( x) 4 x 2 cos x
производную. Тогда
Найти: y
производная от производной
y 12 x 2 2 sin x
первого порядка называется
производной второго порядка
y 24 x 2 cos x
или второй производной и
y 24 x 2 sin x
обозначается так: f "(х).
Итак,
f ( x) f ( x)
f ( x) f ( x)












 Математика
Математика








