Похожие презентации:
Степенная функция. 10 класс
1. Степенная функция
10 классСтепенная
функция
2.
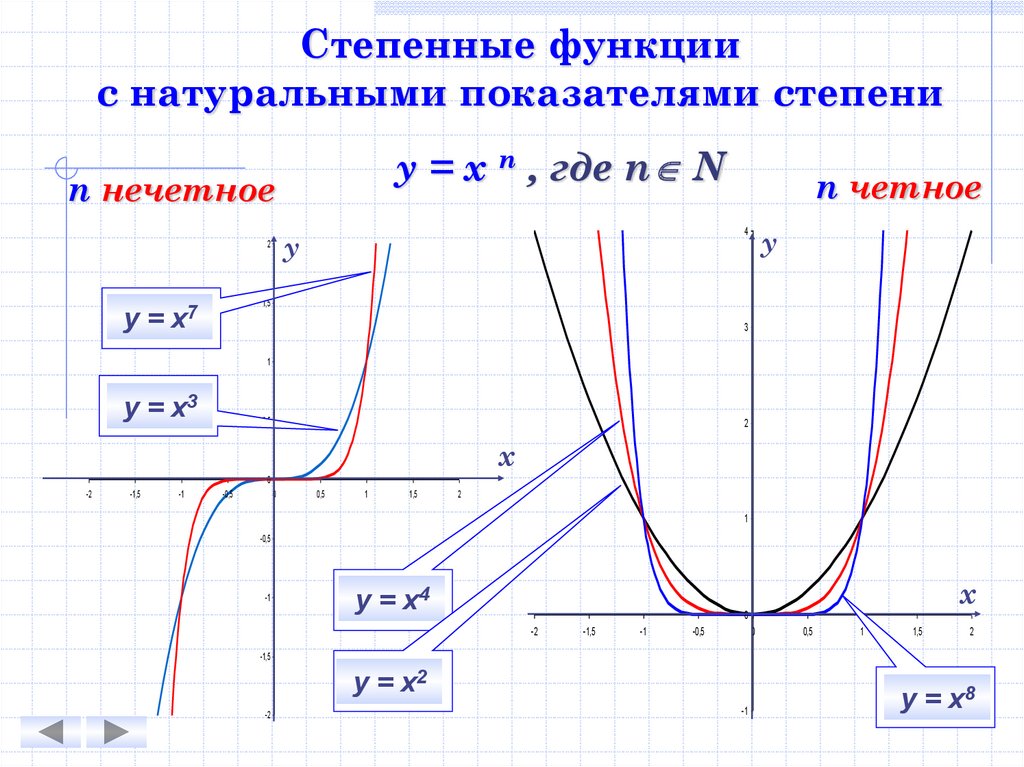
Степенные функциис натуральными показателями степени
у = х n , где n N
n нечетное
у
4
у
2
n четное
1,5
у = х7
3
1
у = х3
0,5
2
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
1
-0,5
-1
у = х4
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-1,5
у = х2
-2
-1
у = х8
3.
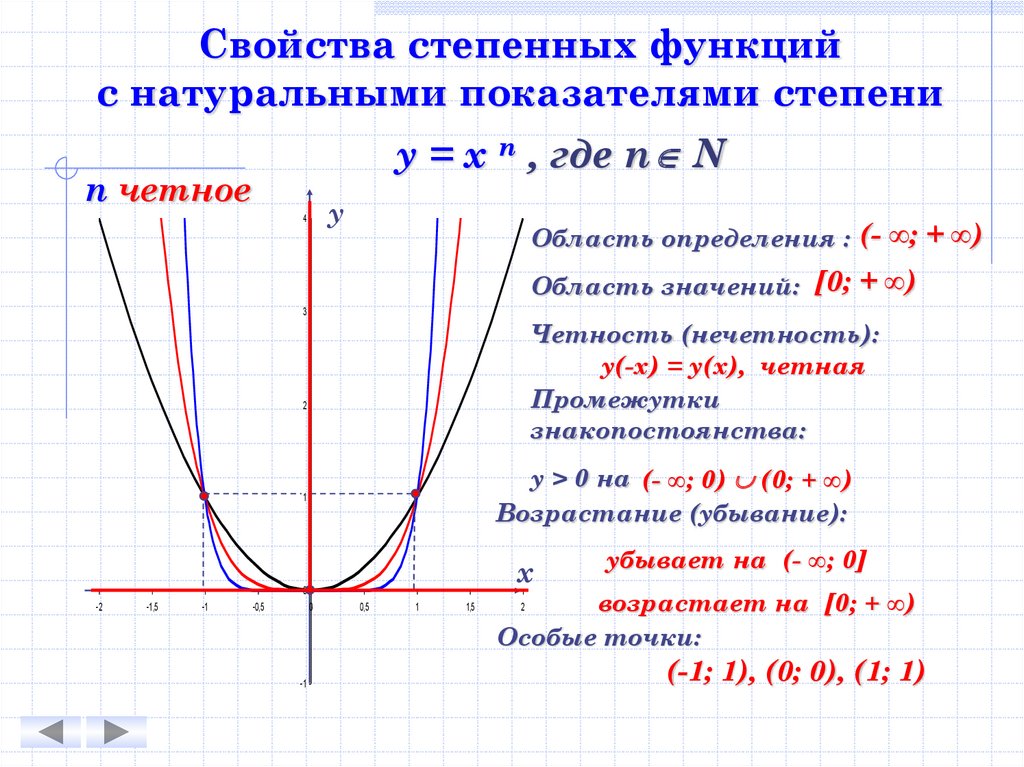
Свойства степенных функцийс натуральными показателями степени
у = х n , где n N
n четное
у
4
Область определения : (- ∞; + ∞)
Область значений: [0; + ∞)
3
Четность (нечетность):
у(-х) = у(х), четная
Промежутки
знакопостоянства:
2
у > 0 на (- ∞; 0) (0; + ∞)
Возрастание (убывание):
1
х
0
-2
-1,5
-1
-0,5
0
-1
0,5
1
1,5
убывает на (- ∞; 0]
возрастает на [0; + ∞)
Особые точки:
2
(-1; 1), (0; 0), (1; 1)
4.
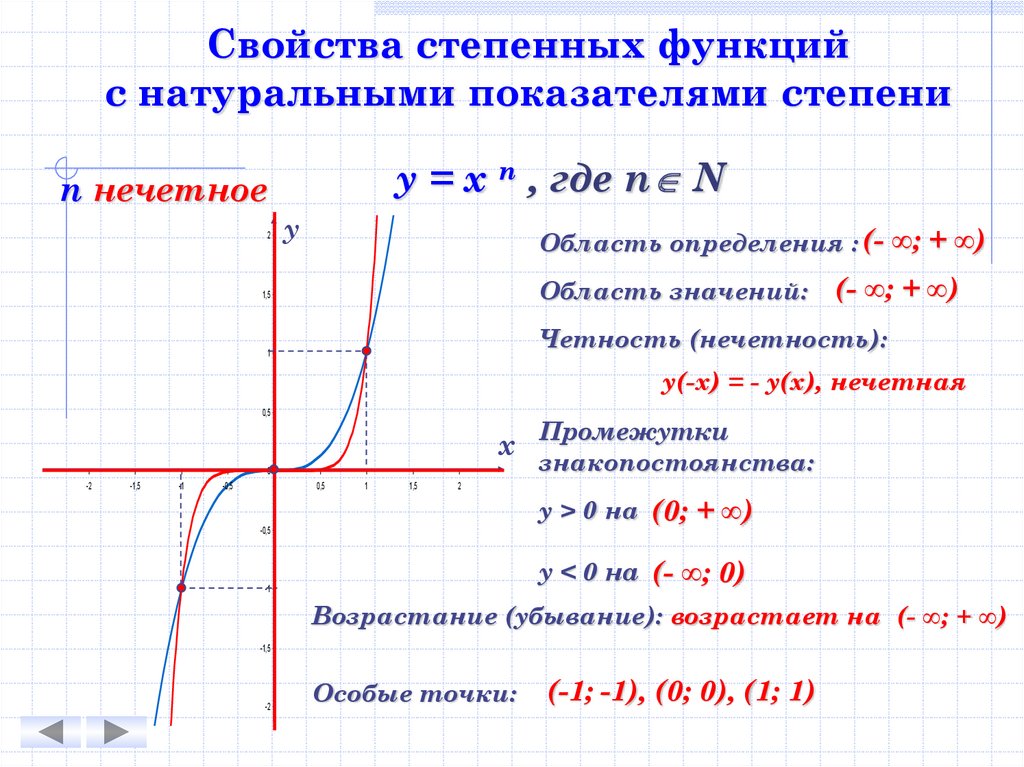
Свойства степенных функцийс натуральными показателями степени
у = х n , где n N
n нечетное
у
2
Область определения : (- ∞; + ∞)
Область значений:
1,5
(- ∞; + ∞)
Четность (нечетность):
1
у(-х) = - у(х), нечетная
0,5
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
Промежутки
знакопостоянства:
2
у > 0 на (0; + ∞)
-0,5
у < 0 на (- ∞; 0)
-1
Возрастание (убывание): возрастает на (- ∞; + ∞)
-1,5
-2
Особые точки:
(-1; -1), (0; 0), (1; 1)
5.
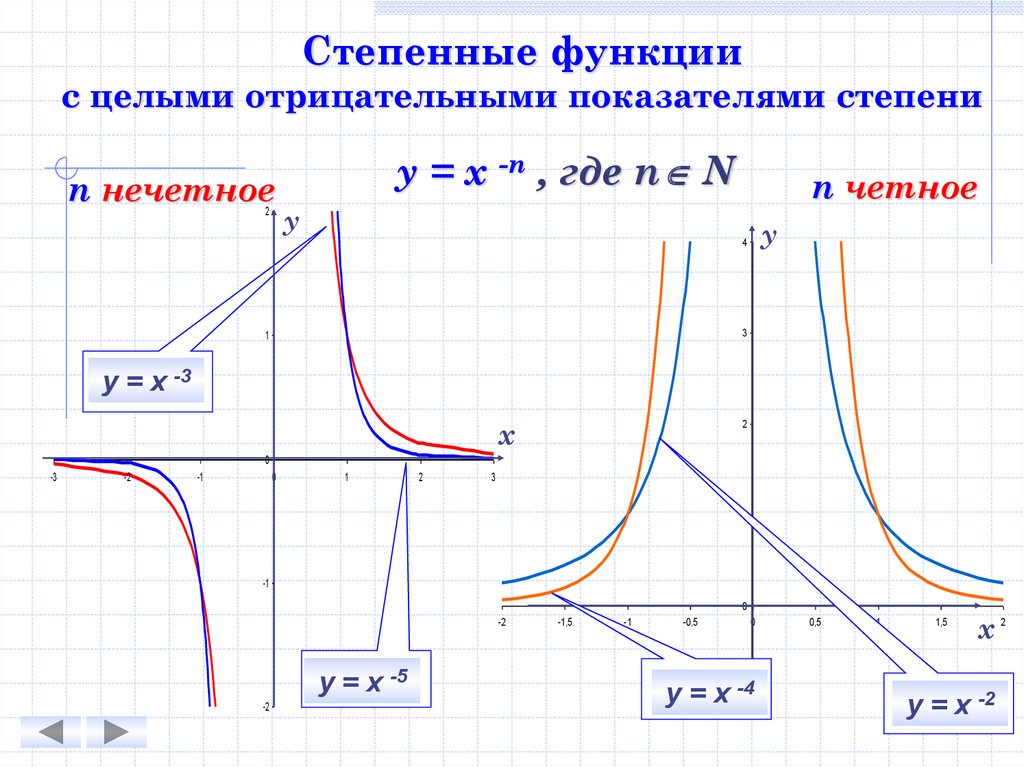
Степенные функциис целыми отрицательными показателями степени
n нечетное
2
у = х -n , где n N
у
n четное
у
4
3
1
у = х -3
х
2
0
-3
-2
-1
0
1
2
3
1
-1
0
-2
у = х -5
-2
-1,5
-1
-0,5
0
у = х -4
-1
0,5
1
1,5
х
у = х -2
2
6.
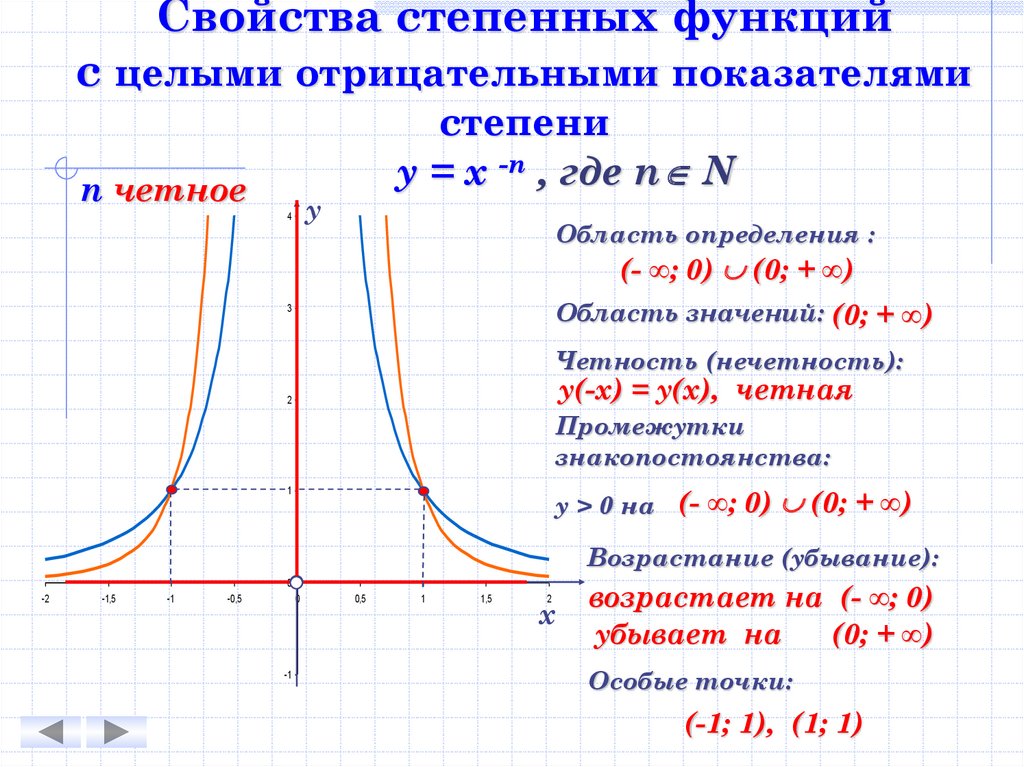
Свойства степенных функцийс целыми отрицательными показателями
n четное
степени
у = х -n , где n N
у
4
Область определения :
(- ∞; 0) (0; + ∞)
Область значений: (0; + ∞)
3
Четность (нечетность):
у(-х) = у(х), четная
2
Промежутки
знакопостоянства:
у > 0 на (- ∞; 0) (0; + ∞)
1
Возрастание (убывание):
0
-2
-1,5
-1
-0,5
0
-1
0,5
1
1,5
2
х
возрастает на (- ∞; 0)
убывает на
(0; + ∞)
Особые точки:
(-1; 1), (1; 1)
7.
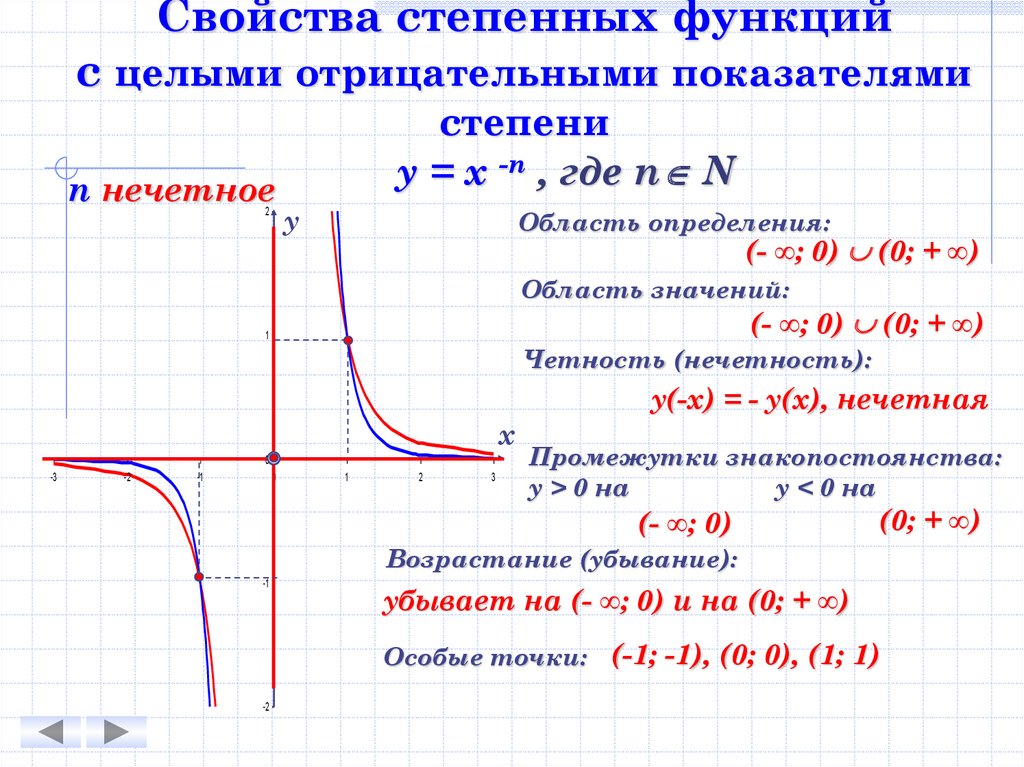
Свойства степенных функцийс целыми отрицательными показателями
n нечетное
2
степени
у = х -n , где n N
у
Область определения:
(- ∞; 0) (0; + ∞)
Область значений:
(- ∞; 0) (0; + ∞)
1
Четность (нечетность):
у(-х) = - у(х), нечетная
х
0
-3
-2
-1
0
1
2
3
Промежутки знакопостоянства:
у > 0 на
у < 0 на
(- ∞; 0)
(0; + ∞)
Возрастание (убывание):
-1
убывает на (- ∞; 0) и на (0; + ∞)
Особые точки: (-1; -1), (0; 0), (1; 1)
-2
8.
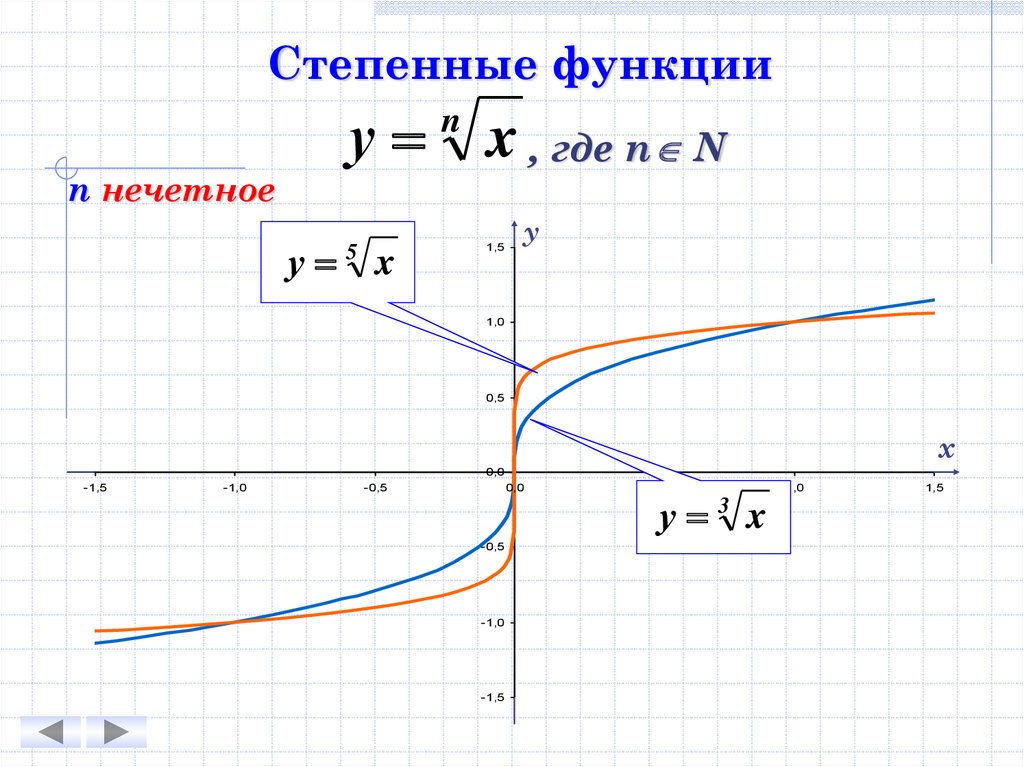
Степенные функцииу
n нечетное
у
5
x
n
x , где n N
1,5
у
1,0
0,5
х
0,0
-1,5
-1,0
0,0
-0,5
-0,5
-1,0
-1,5
0,5
у 3 x
1,0
1,5
9.
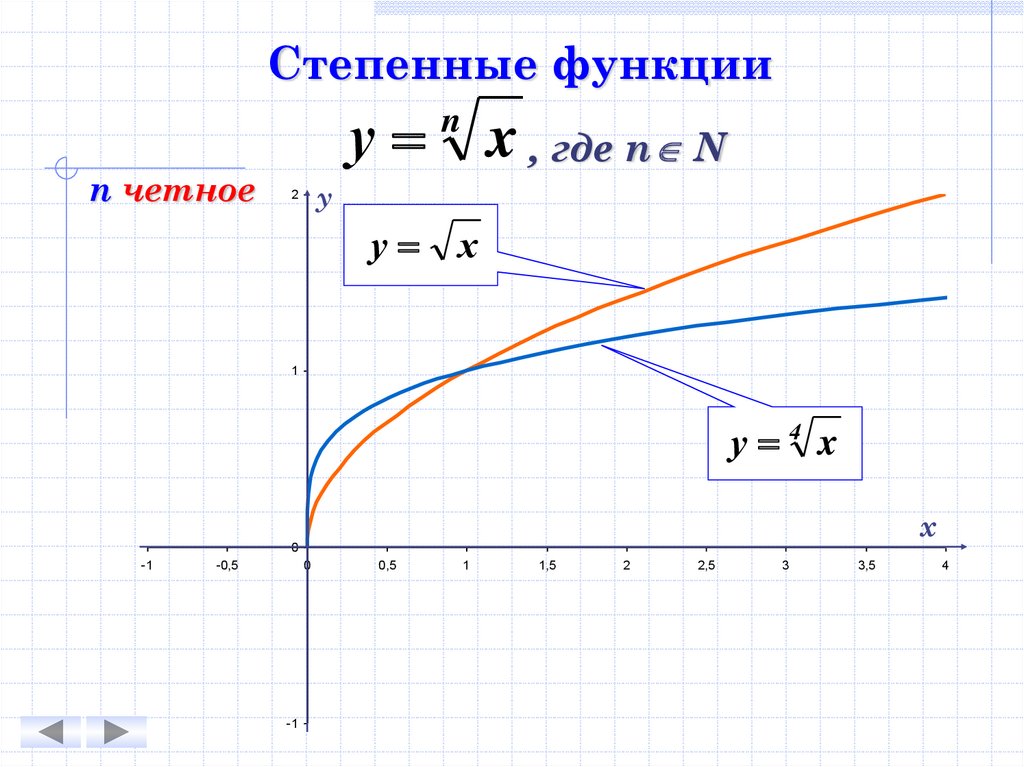
Степенные функцииn четное
у
n
x , где n N
у
2
у
х
1
у 4 x
х
0
-1
-0,5
0
-1
0,5
1
1,5
2
2,5
3
3,5
4
10.
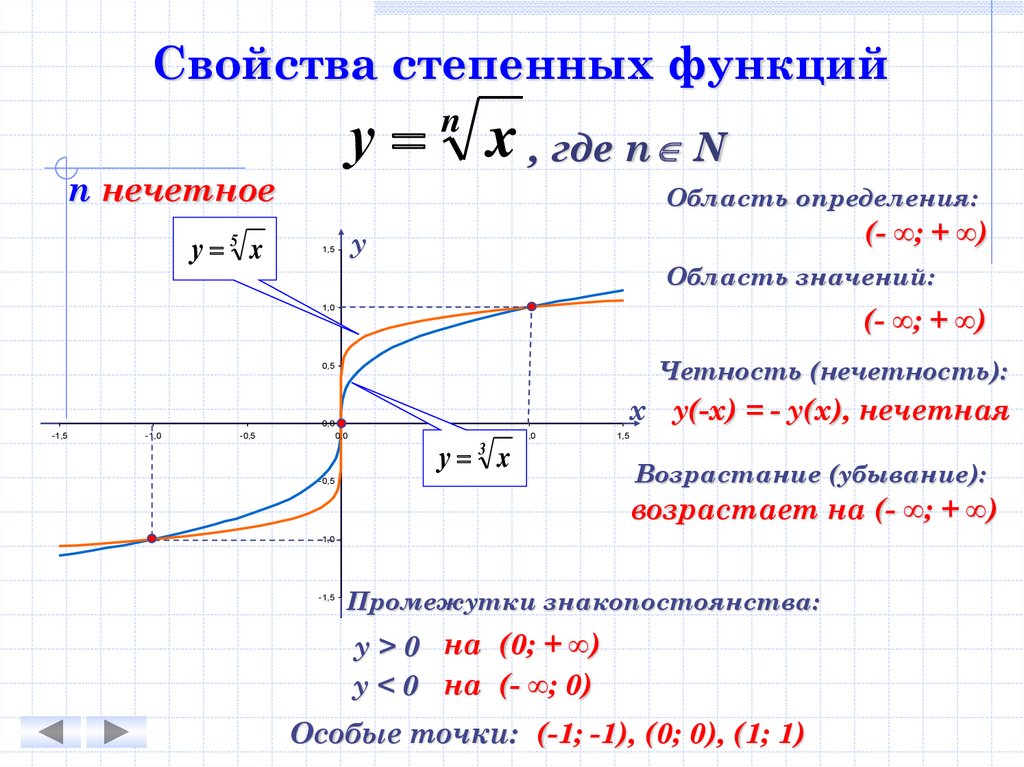
Свойства степенных функцийу
n нечетное
у 5 x
n
x , где n N
Область определения:
(- ∞; + ∞)
у
1,5
Область значений:
(- ∞; + ∞)
1,0
Четность (нечетность):
0,5
х у(-х) = - у(х), нечетная
0,0
-1,5
-1,0
-0,5
0,0
0,5
у x
1,0
3
-0,5
1,5
Возрастание (убывание):
возрастает на (- ∞; + ∞)
-1,0
-1,5
Промежутки знакопостоянства:
у > 0 на (0; + ∞)
у < 0 на (- ∞; 0)
Особые точки: (-1; -1), (0; 0), (1; 1)
11.
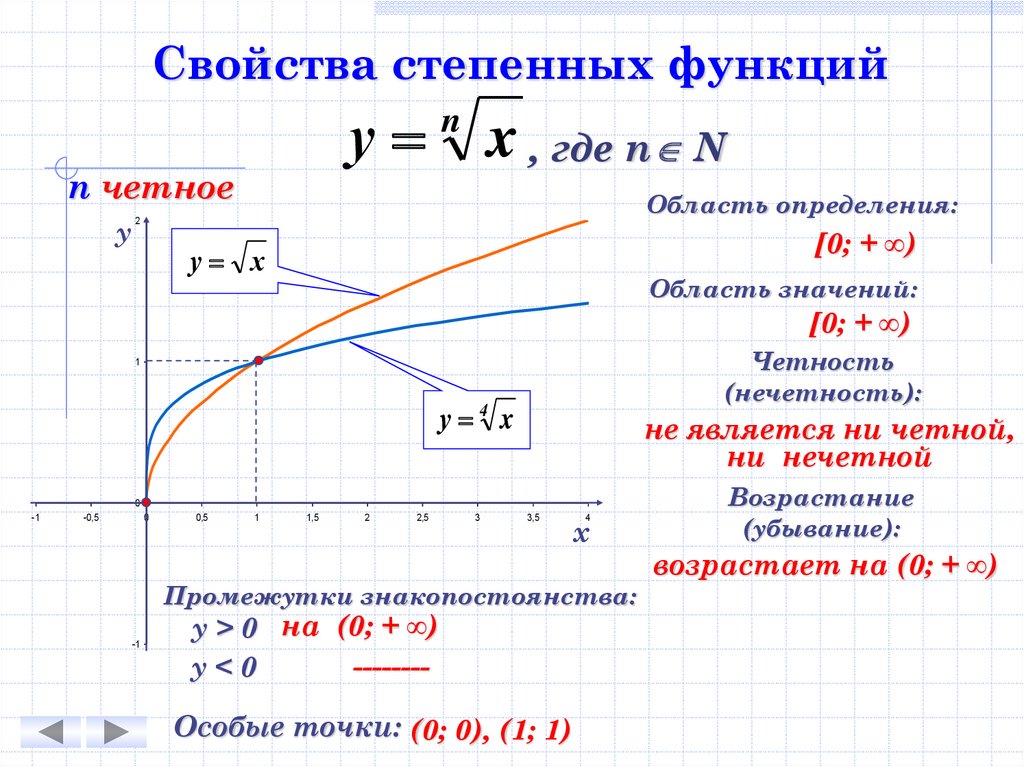
Свойства степенных функцийу
n четное
у
n
x , где n N
Область определения:
2
[0; + ∞)
у х
Область значений:
[0; + ∞)
Четность
(нечетность):
1
у 4 x
не является ни четной,
ни нечетной
0
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
х
Промежутки знакопостоянства:
-1
у > 0 на (0; + ∞)
-------у<0
Особые точки: (0; 0), (1; 1)
Возрастание
(убывание):
возрастает на (0; + ∞)
12.
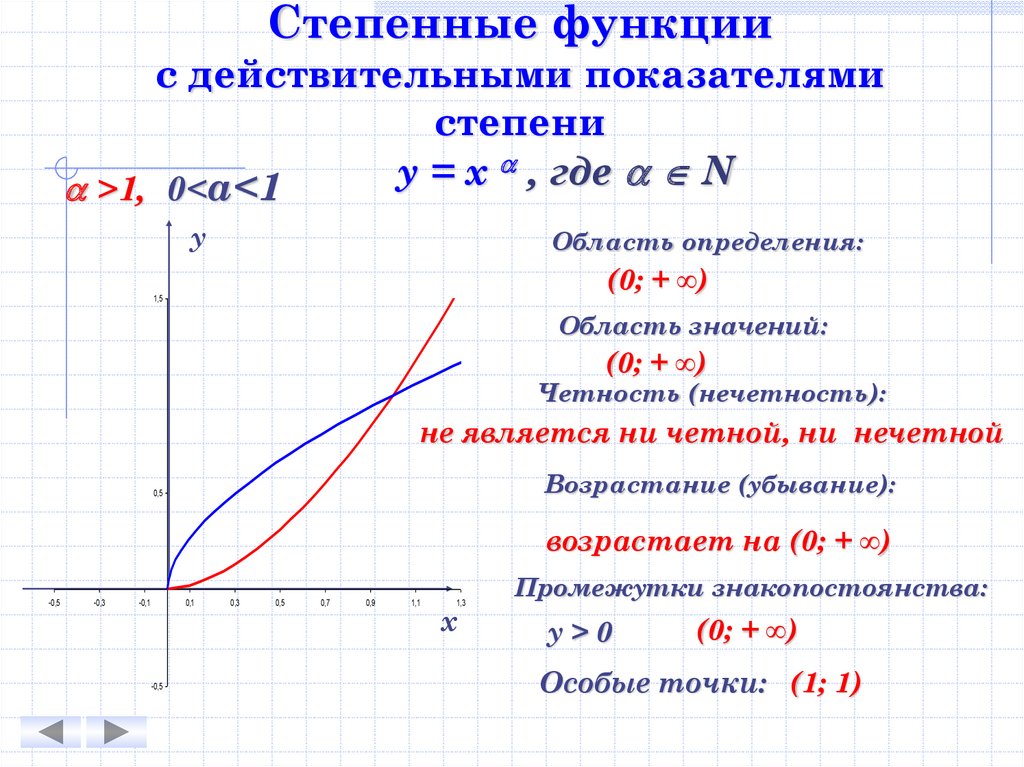
Степенные функциис действительными показателями
степени
, где N
у
=
х
>1, 0<а<1
у
Область определения:
(0; + ∞)
1,5
Область значений:
(0; + ∞)
Четность (нечетность):
не является ни четной, ни нечетной
Возрастание (убывание):
0,5
возрастает на (0; + ∞)
-0,5
-0,3
-0,1
0,1
-0,5
0,3
0,5
0,7
0,9
1,1
1,3
х
Промежутки знакопостоянства:
у>0
(0; + ∞)
Особые точки: (1; 1)
13.
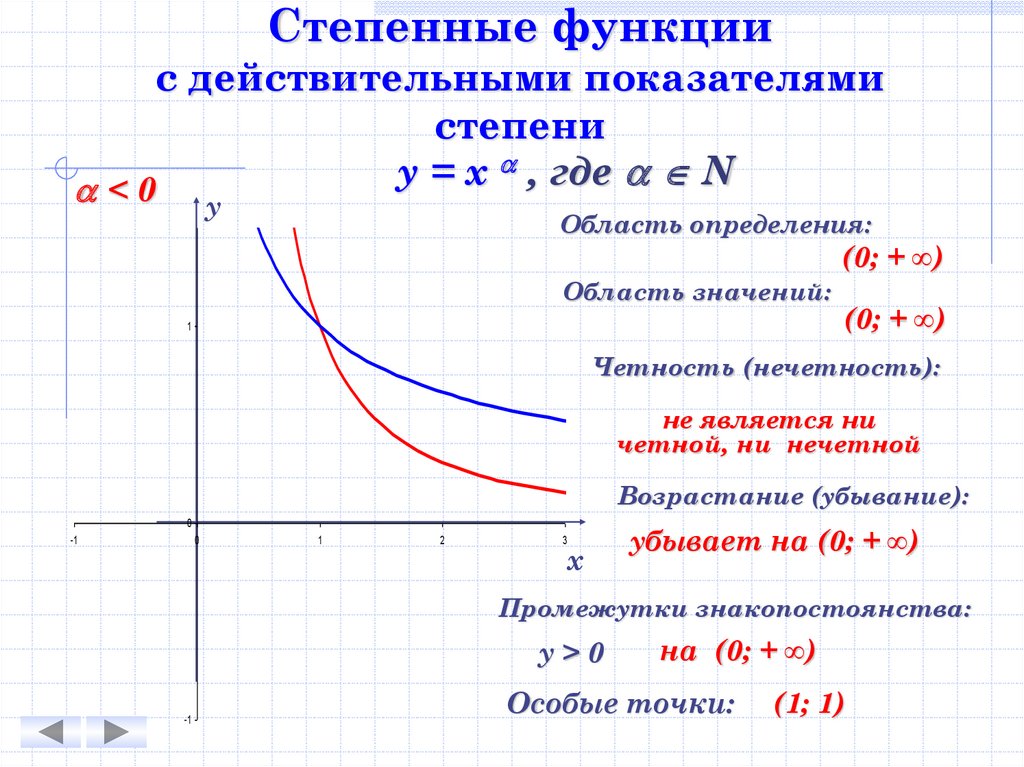
Степенные функциис действительными показателями
степени
, где N
у
=
х
<0
у
Область определения:
(0; + ∞)
Область значений:
1
(0; + ∞)
Четность (нечетность):
не является ни
четной, ни нечетной
Возрастание (убывание):
0
-1
0
1
2
3
х
убывает на (0; + ∞)
Промежутки знакопостоянства:
у>0
-1
на (0; + ∞)
Особые точки:
(1; 1)
14.
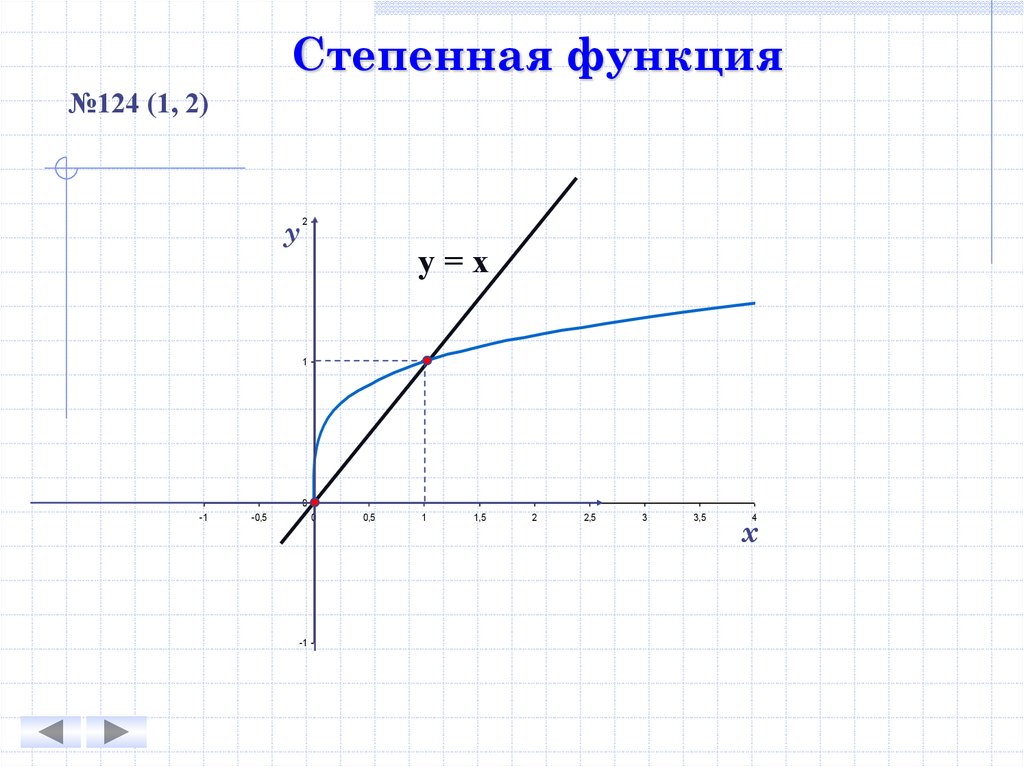
Степенная функция№124 (1, 2)
у
2
у=х
1
0
-1
-0,5
0
-1
0,5
1
1,5
2
2,5
3
3,5
4
х
15.
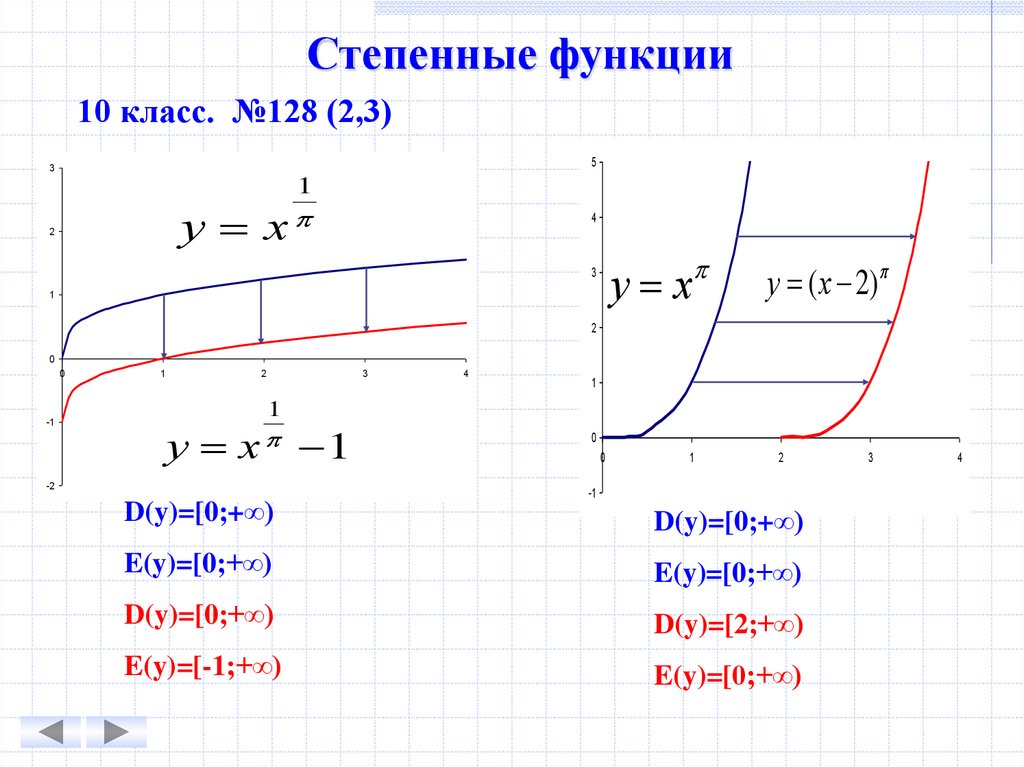
Степенные функции10 класс. №128 (2,3)
5
3
1
у х
2
4
у х
3
1
у ( х 2)
2
0
0
-1
1
2
3
4
1
1
у х 1
-2
0
0
1
2
-1
D(y)=[0;+∞)
D(y)=[0;+∞)
E(y)=[0;+∞)
E(y)=[0;+∞)
D(y)=[0;+∞)
D(y)=[2;+∞)
E(y)=[-1;+∞)
E(y)=[0;+∞)
3
4
16. Список литературы
Алимов Ш.А. Алгебра и начала анализа: Учебник для 10-11 кл.общеобразовательных учреждений. – М.: Просвещение, 2005.
Федорова Н.Е. Изучение алгебры и начал анализа в 10-11
классах. – М.: Просвещение, 2004.
Генденштейн Л.Э., Ершова А.П., Ершова А.С. Наглядный
справочник по алгебре и началам анализа с примерами для 7-11
классов. – М.: Илекса, Гимназия, 1997.


 Математика
Математика








