Похожие презентации:
Синус, косинус, тангенс угла
1.
Урок №24Задание:
1.Составить конспект по презентации.
2. Записать в рабочую тетрадь примеры из учебника Лисичкина В.Т.
Вводная глава стр 34 №342,345,358
4. Записать в рабочую тетрадь таблицу значений тригонометрических
функций стр. 36
3. Пройти тест «Синус, косинус, тангенс»
2.
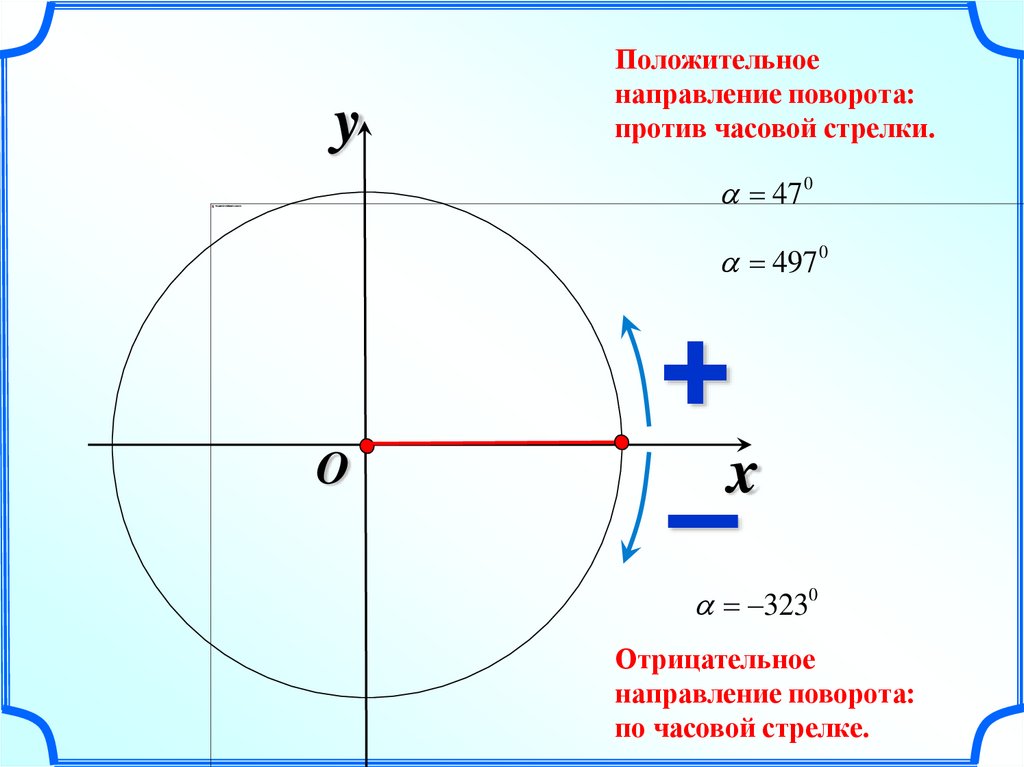
yПоложительное
направление поворота:
против часовой стрелки.
47 0
497 0
O
+
x
–
3230
Отрицательное
направление поворота:
по часовой стрелке.
3.
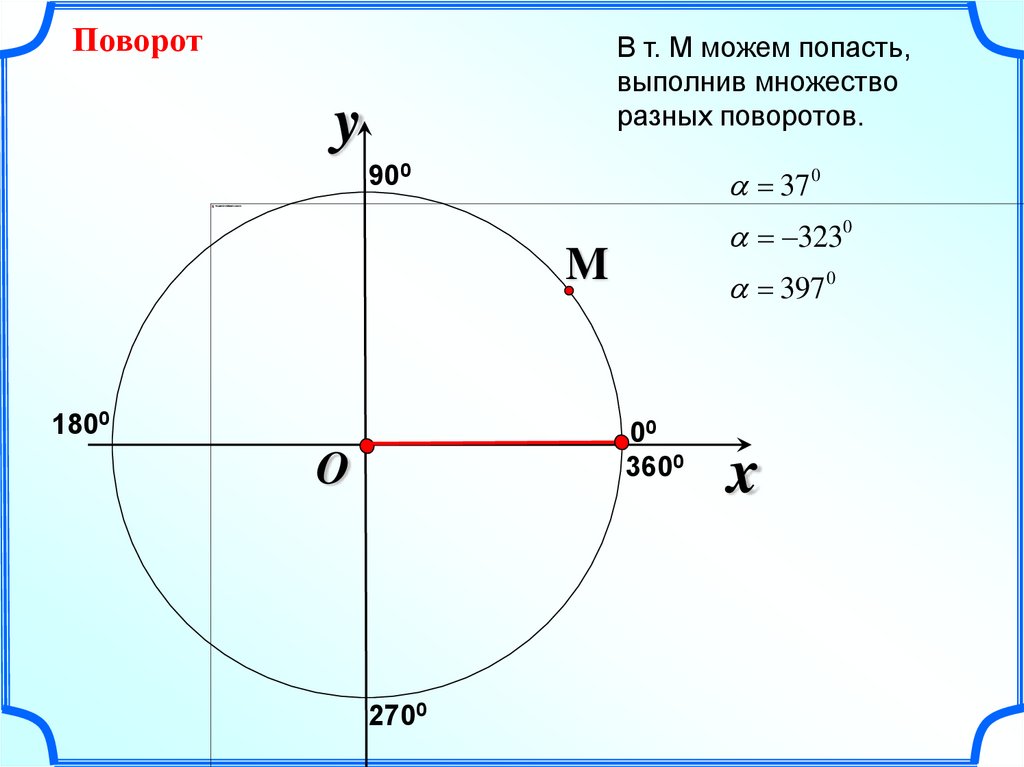
ПоворотВ т. М можем попасть,
выполнив множество
разных поворотов.
y
37 0
900
3230
M
1800
3970
00
3600
O
2700
x
4.
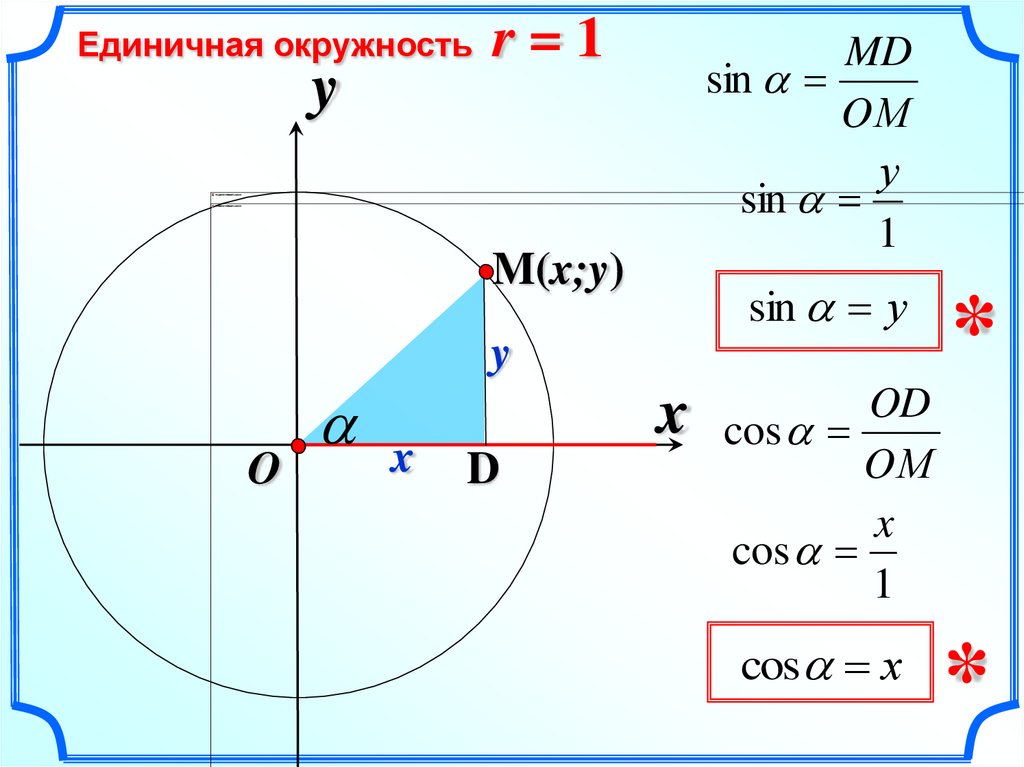
Единичная окружностьy
r=1
MD
sin
OМ
у
sin
1
M(x;y)
sin у
y
O
x
x
D
*
OD
cos
OМ
x
cos
1
cos х
*
5.
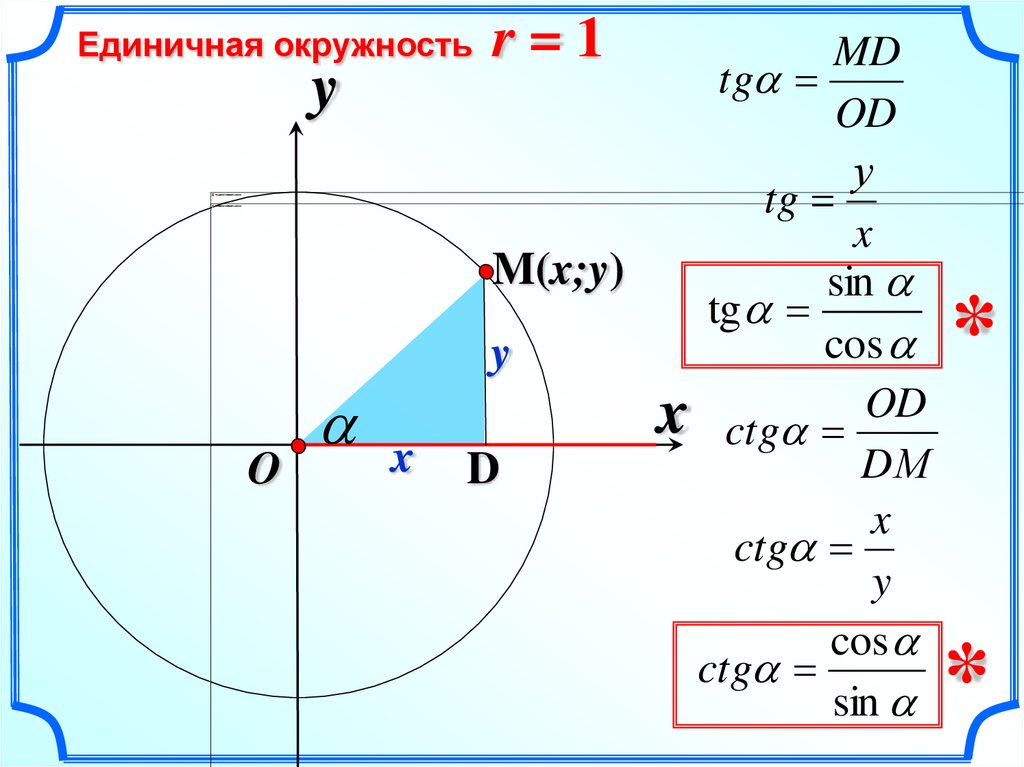
Единичная окружностьy
O
x
r=1
MD
tg
OD
у
tg
x
M(x;y)
sin
tg
cos
y
x ctg OD
DМ
D
x
ctg
y
cos
ctg
sin
*
*
6.
Cинусом углакосинусом угла
называется ордината
y точки М, а
– абсцисса x точки М.
sin a = y; cos a = x
sin
tg
cos
cos
ctg
sin
sin cos
1
tg ctg
cos sin
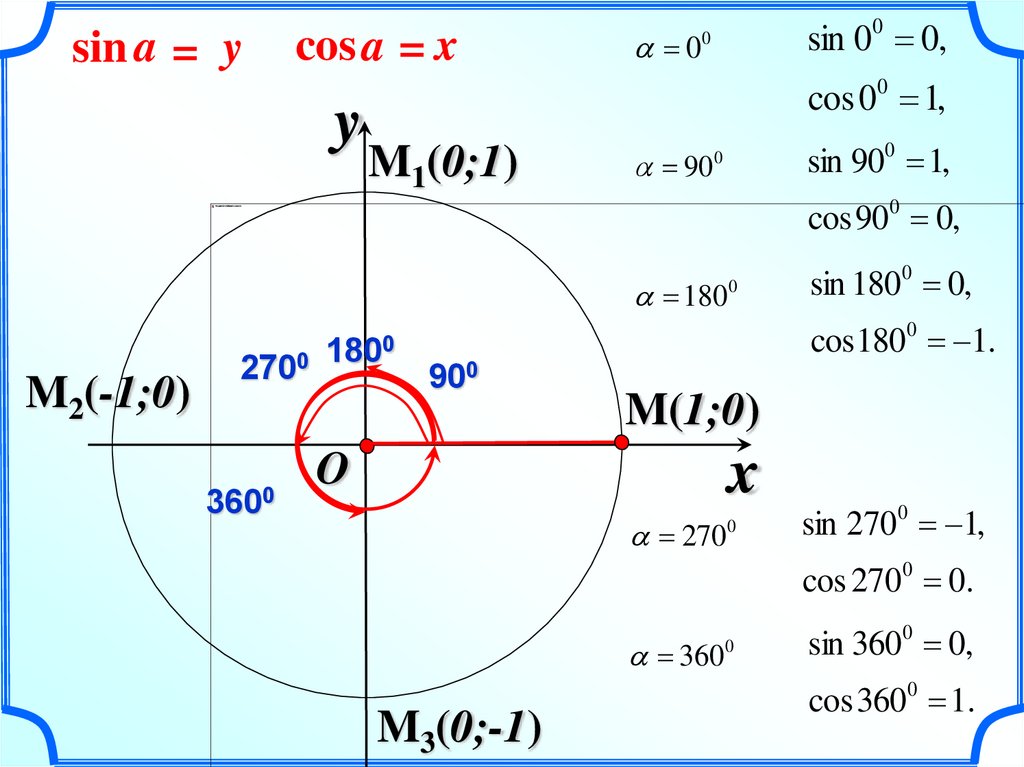
7.
sin a = ycos a = x
y
0
sin 00 0,
0
cos 00 1,
M1(0;1)
90
sin 900 1,
0
cos 900 0,
180
M2(-1;0)
2700
3600
1800
0
sin 1800 0,
cos1800 1.
900
M(1;0)
x
O
270
0
sin 2700 1,
cos 2700 0.
360
M3(0;-1)
0
sin 3600 0,
cos 3600 1.
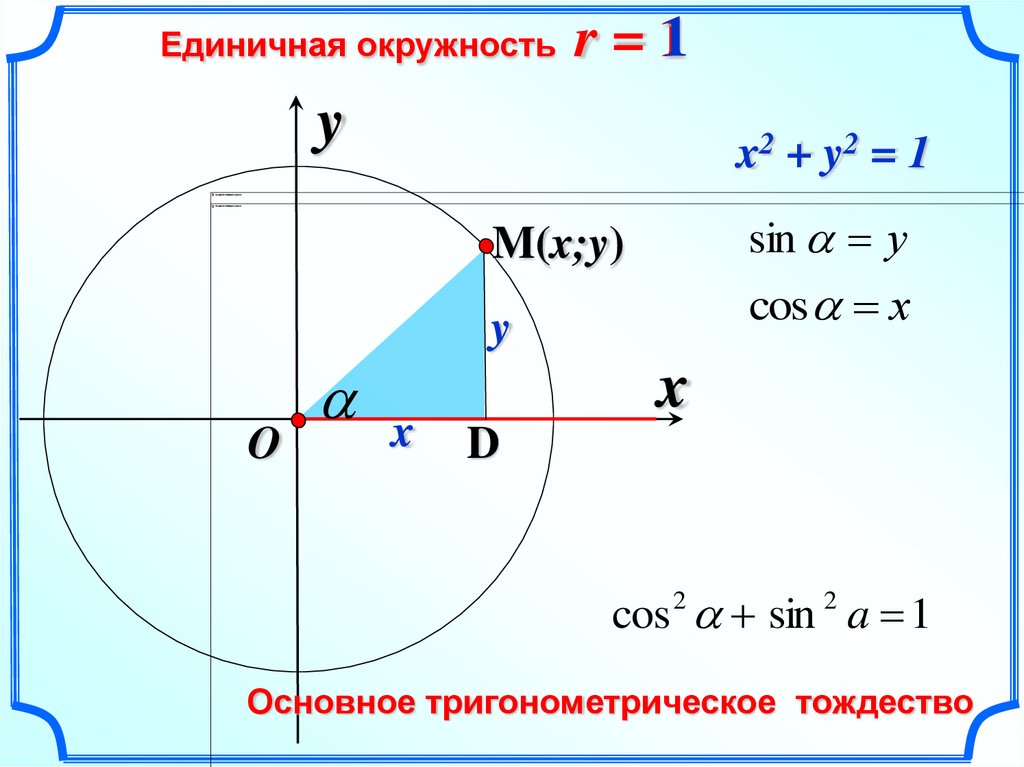
8.
Единичная окружностьr=1
y
x2 + y2 = 1
sin у
M(x;y)
cos х
y
O
x
x
D
cos sin a 1
2
2
Основное тригонометрическое тождество
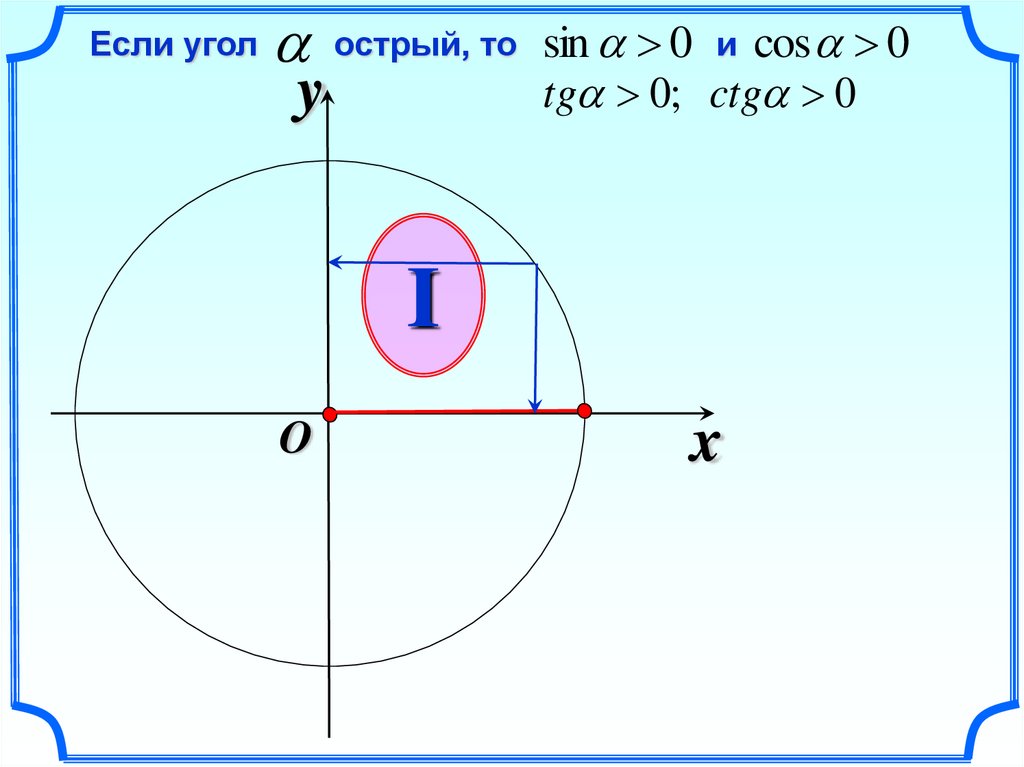
9.
Если уголострый, то
y
sin 0 и cos 0
tg 0; ctg 0
I
O
x
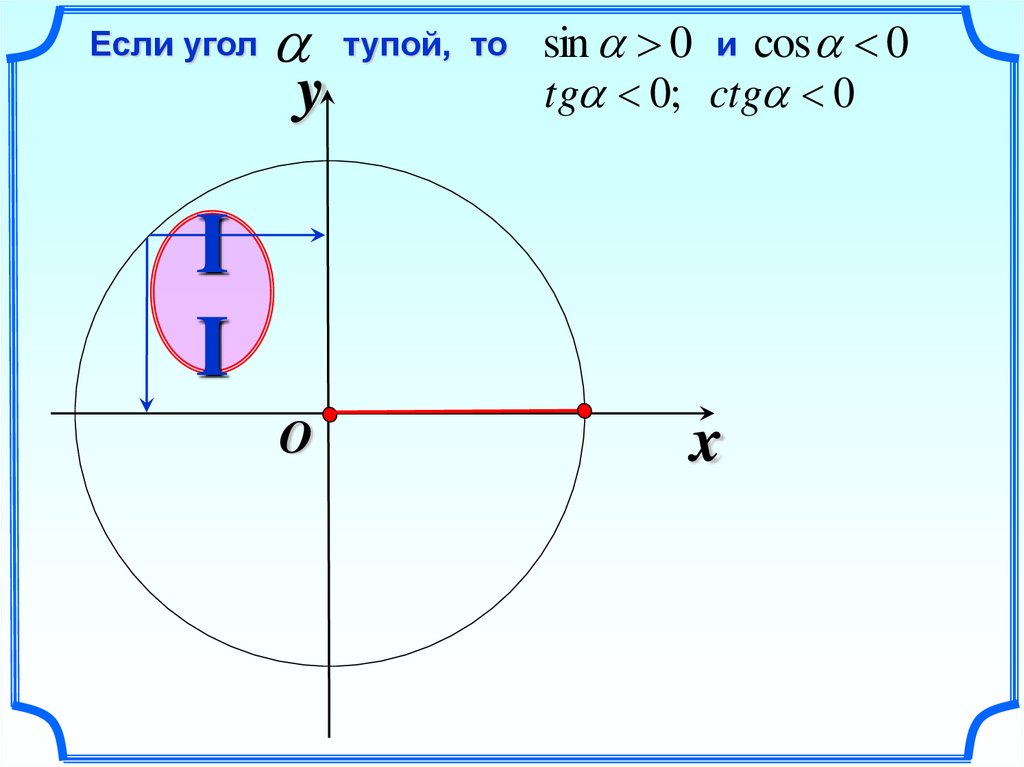
10.
Если уголy
тупой, то
sin 0 и cos 0
tg 0; ctg 0
I
I
O
x
11.
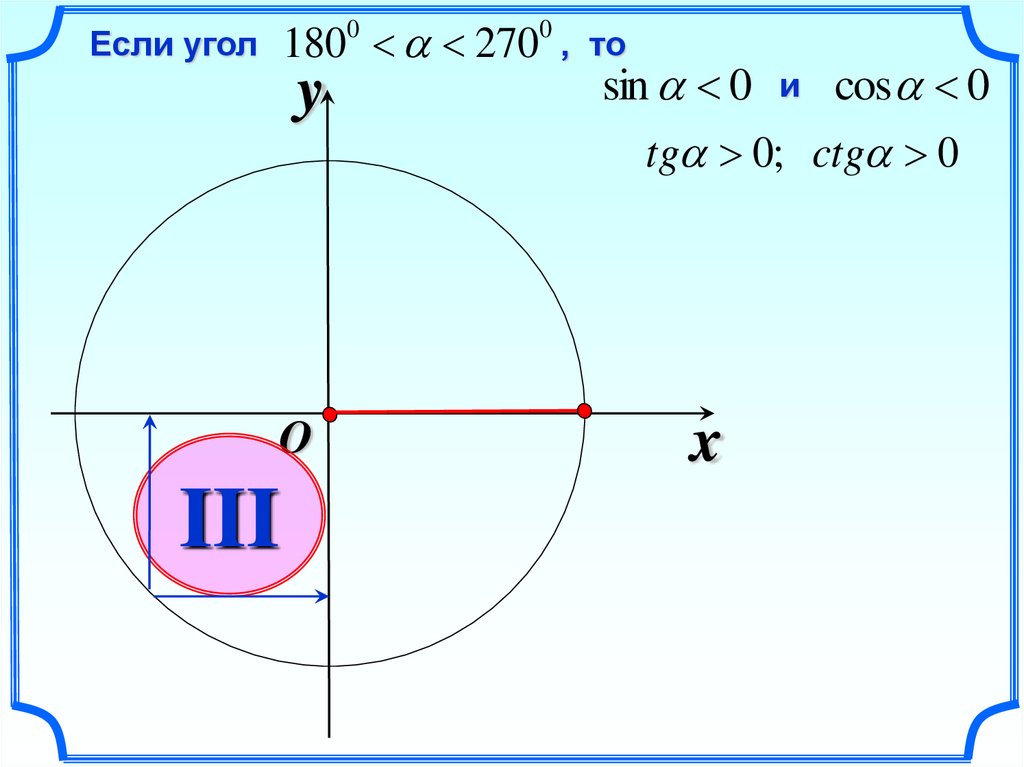
180 2700
Если угол
y
O
III
0
, то
sin 0 и cos 0
tg 0; ctg 0
x
12.
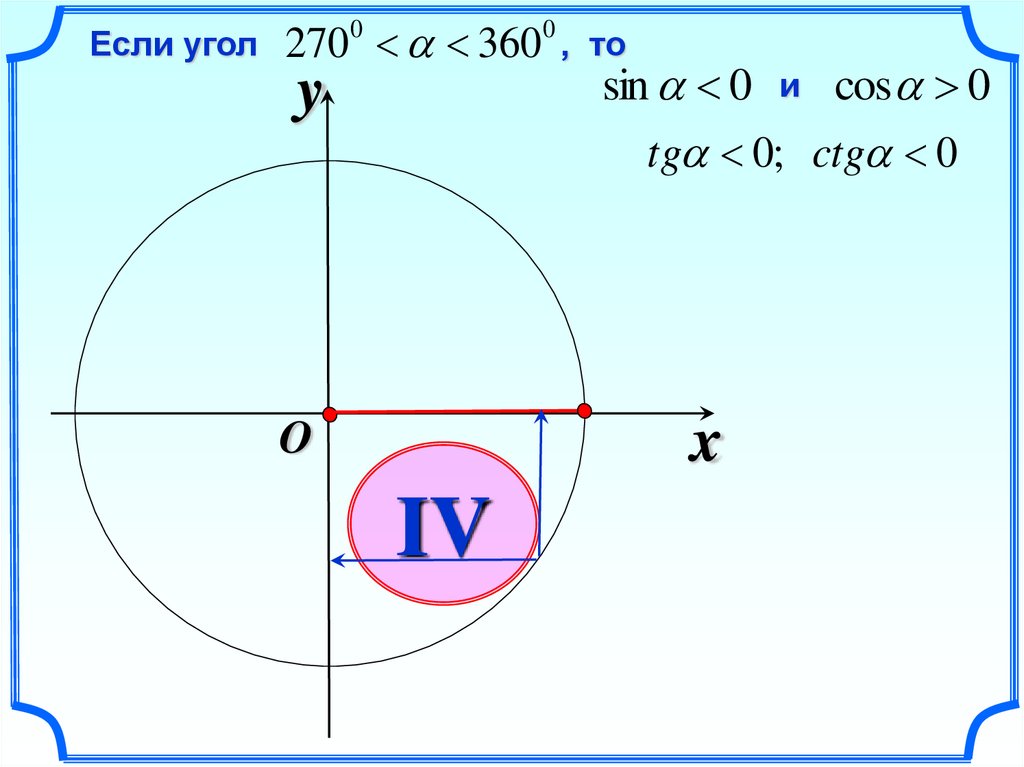
Если угол270 360
0
y
0
, то
sin 0 и cos 0
tg 0; ctg 0
x
O
IV
13.
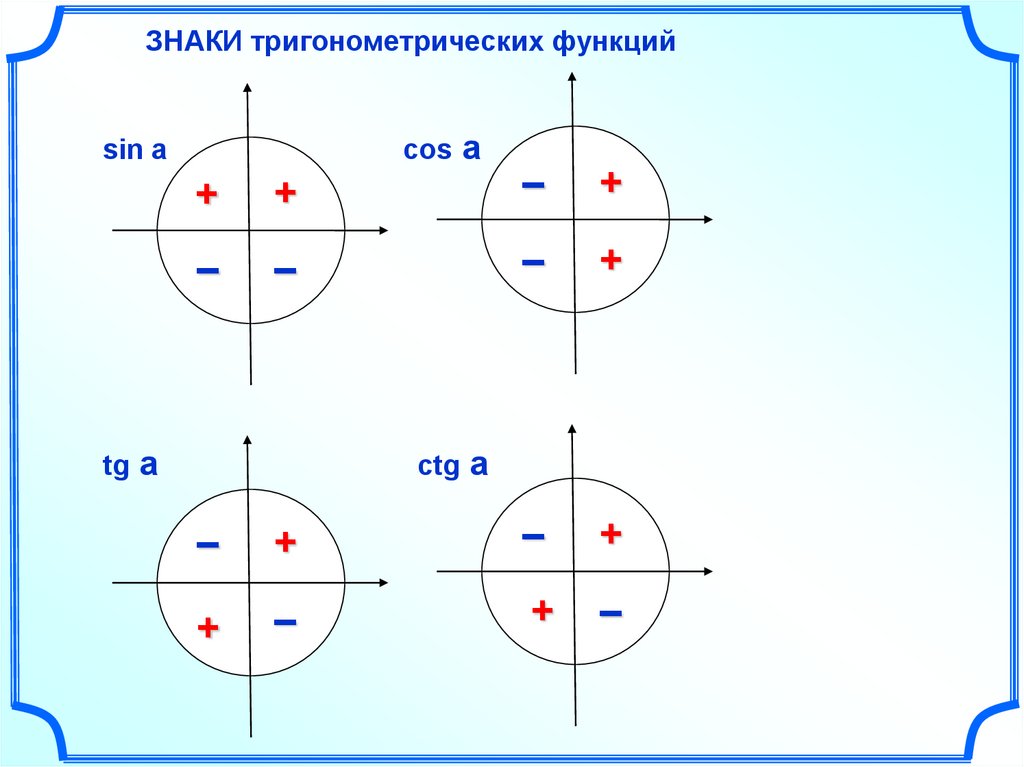
ЗНАКИ тригонометрических функцийcos a
sin a
+
+
–
+
–
–
–
+
tg a
ctg a
–
+
–
+
+
–
+
–
14.
ysin( ) sin
sin
O
sin( )
x
f ( x)
f (x)
Функция нечетная
15.
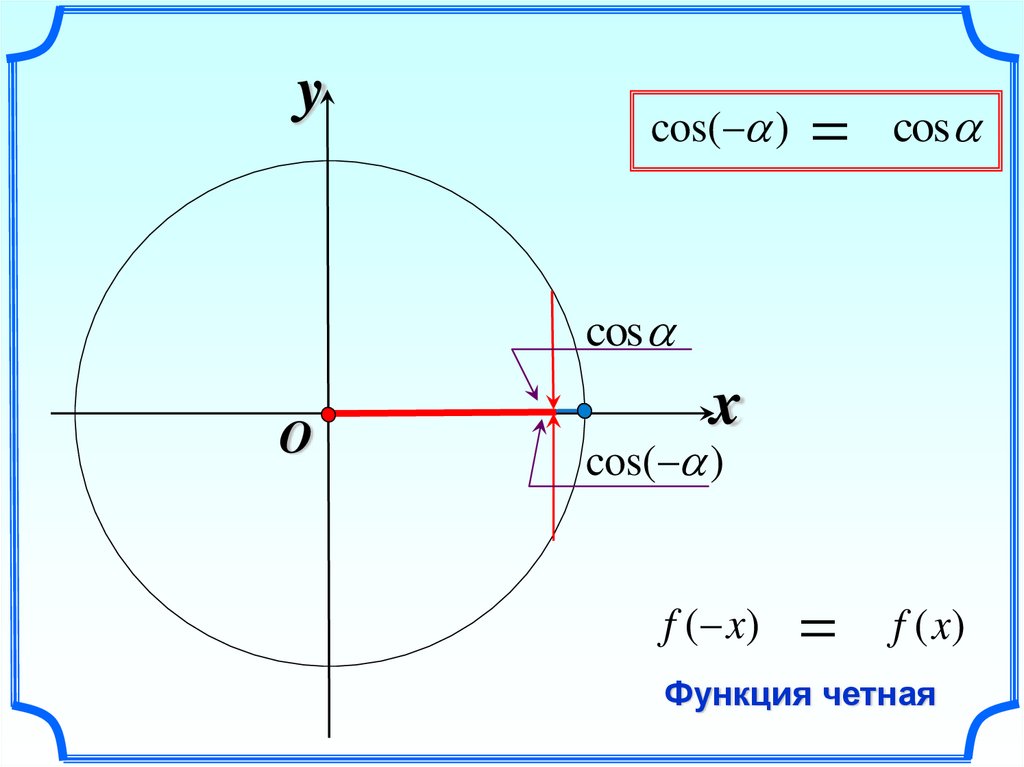
ycos( )
cos
f (x)
cos
O
x
cos( )
f ( x)
Функция четная
16.
sintg
cos
sin
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x)
f (x)
Функция нечетная
Докажи самостоятельно
tg( ) tg
ctg( ) ctg
17.
f ( x)f (x)
Функция четная
cos( )
cos
f ( x)
f (x)
Функция нечетная
sin( ) sin
tg( ) tg
ctg( ) ctg
18.
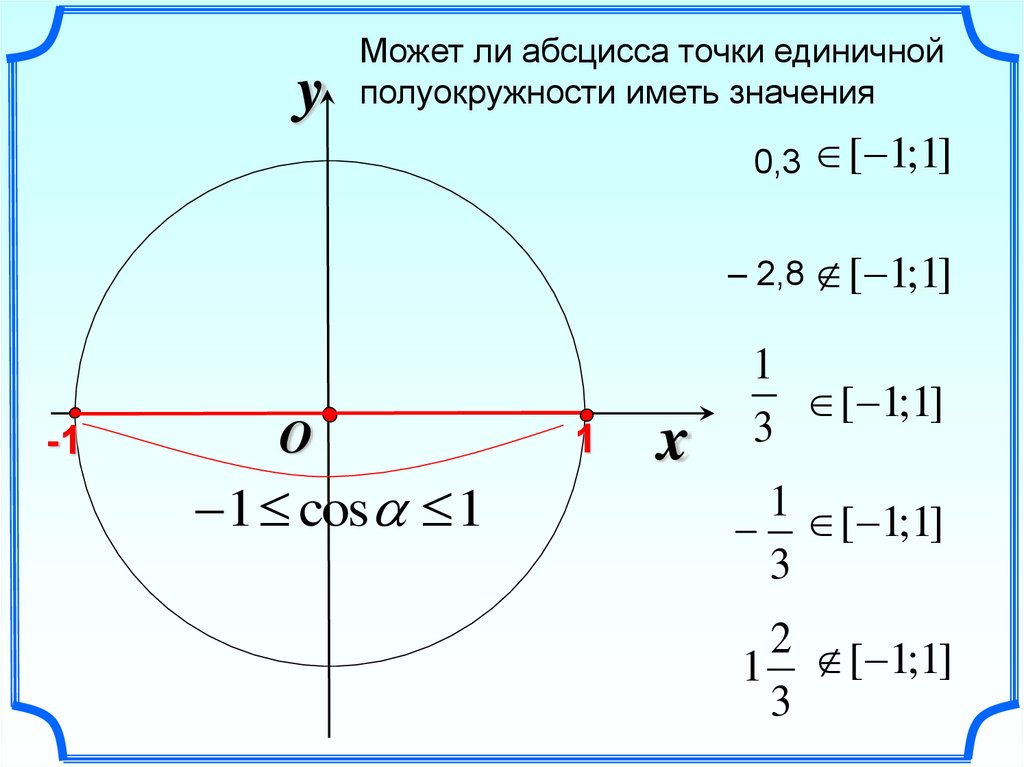
yМожет ли абсцисса точки единичной
полуокружности иметь значения
0,3
[ 1;1]
– 2,8 [ 1;1]
-1
O
1 cos 1
1
x
1
[ 1;1]
3
1 [ 1;1]
3
2 [ 1;1]
1
3
19.
yМожет ли ордината точки единичной
полуокружности иметь значения
1
0,6
[ 1;1]
– 0,3 [ 1;1]
1 sin 1
x
O
7 [ 1;1]
1
7
-1
[ 1;1]
1,002 [ 1;1]






 Математика
Математика








