SINUS_KOSINUS

1. Радианное измерение углов

Тригонометрические
функции числового
аргумента

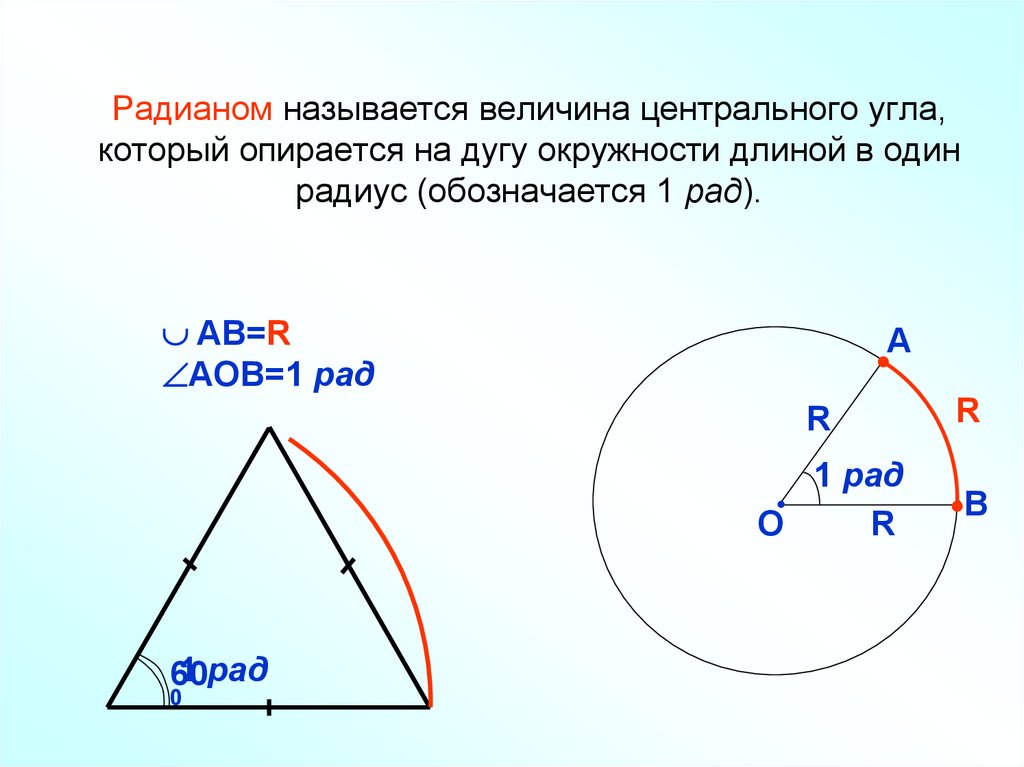
2. Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад).

AB=R
AOB=1 рад
1 рад
60
0
A
R
R
1 рад
O
R
B

3.

3,14159... 3,14
1800 – рад
х0
– 1 рад
3600 – 2 рад

4.

№ 6.1 Выразите угол в
радианах :
40 х рад
0
180 рад
0
40 2
х
180
9

5.

№ 6.2 Найдите градусную
меру угла:
0 ,1 180
0,1 180 18
9
20
20
0
2 рад х 0
3 3 180 0 0
135
3,414 рад 4 180
0
0
0
0

6.

Выразите угол в радианах
с помощью :
3
270°=
- 90°=
720°= 4
30°=
2
7
2
6 2 60°=
360°=
180°= - 210°=
6
3
45°=
4

7.

Найдите градусную меру
угла, радианная мера
которого равна:
53 2
540°
300°
72°
18°
33 10
108°
55

8.

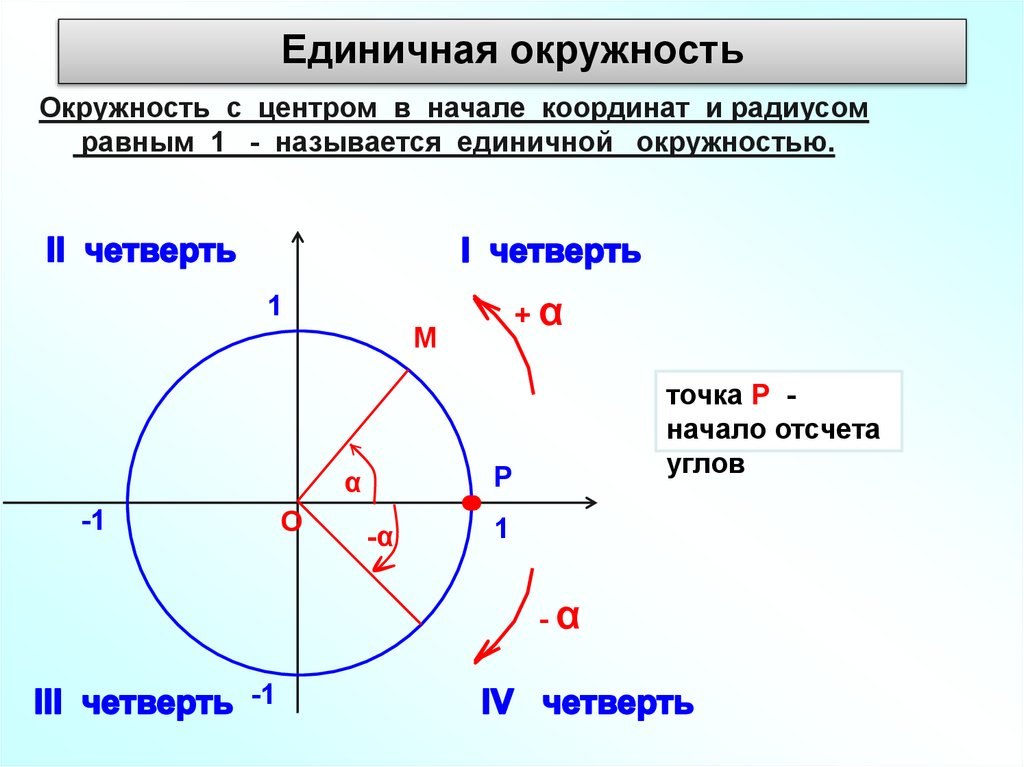
Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
+α
1
М
Р
α
О
-1
точка Р начало отсчета
углов
-α
1
-α
-1

9.

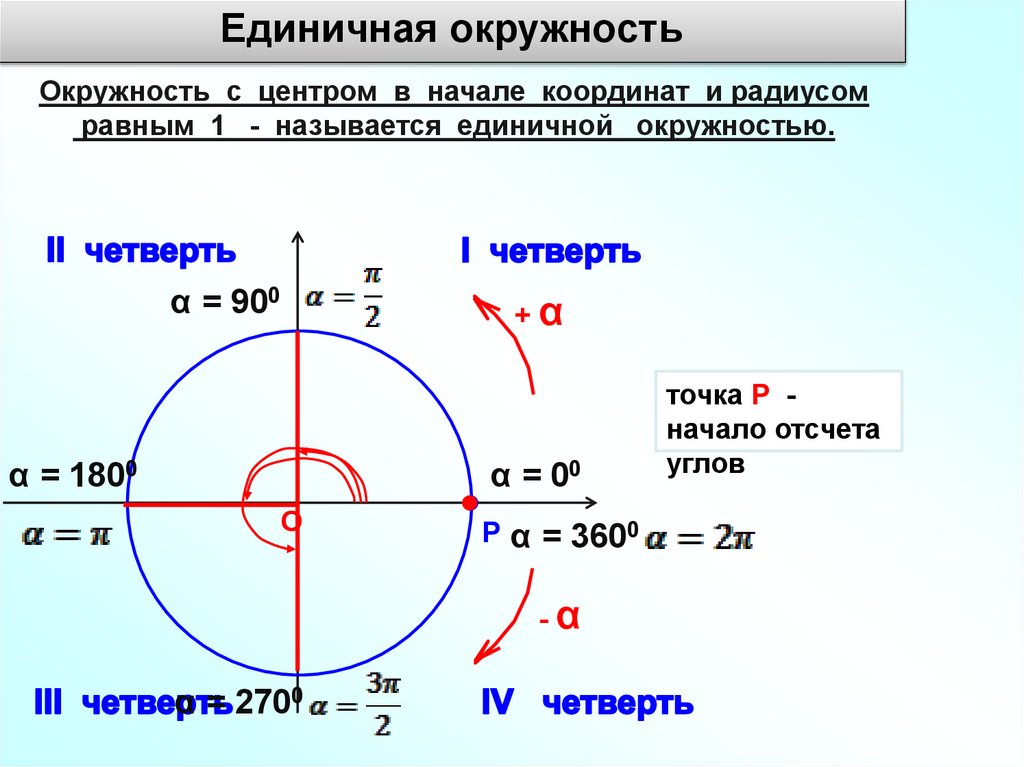
Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
α = 900
α = 1800
+α
α = 00
О
Р α = 3600
-α
α = 2700
точка Р начало отсчета
углов

10.

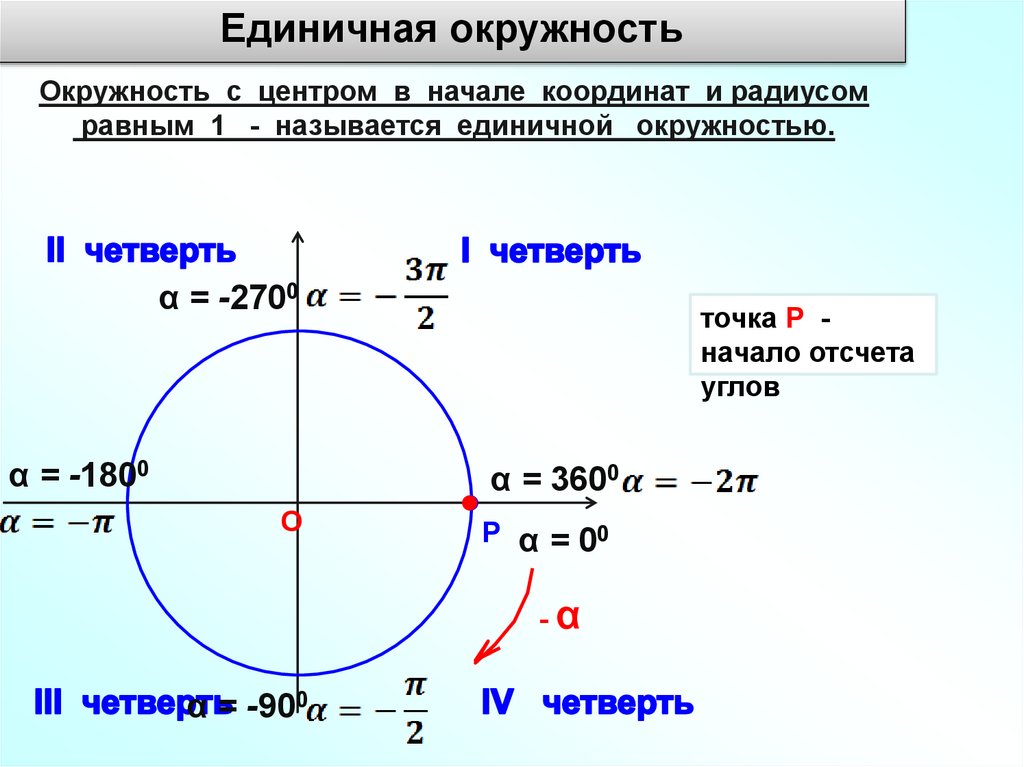
Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
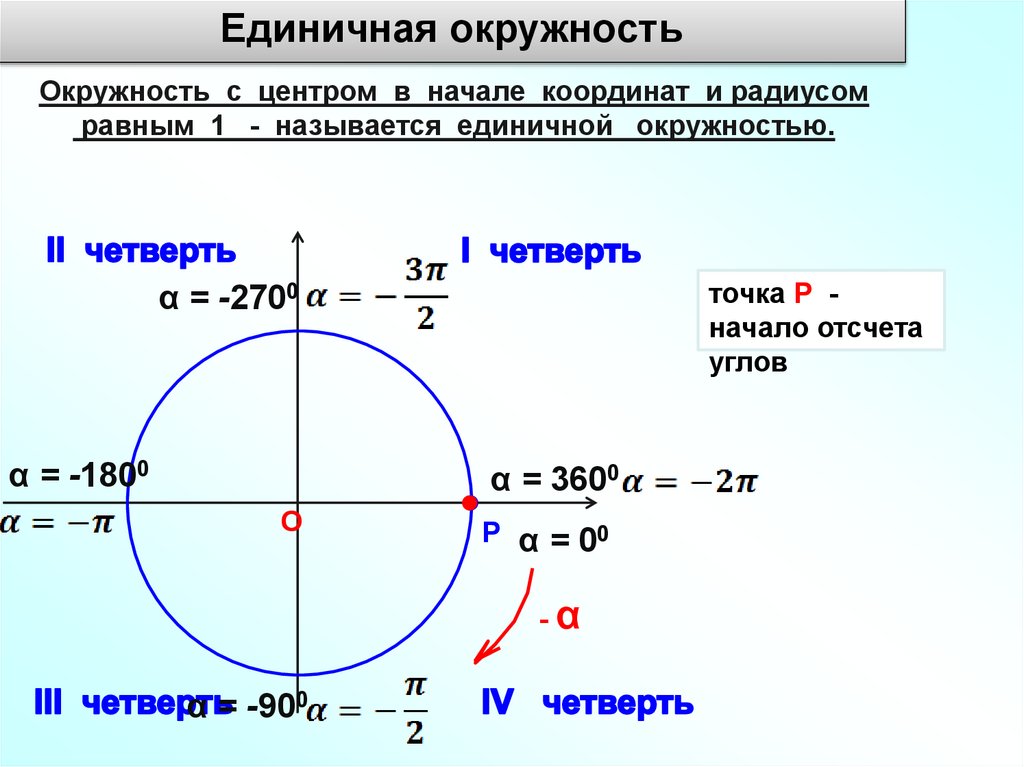
α = -2700
α = -1800
точка Р начало отсчета
углов
α = 3600
О
Р α = 00
-α
α = -900

11.

Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
точка Р начало отсчета
углов
α = -2700
α = -1800
α = 3600
О
Р α = 00
-α
α = -900

12.

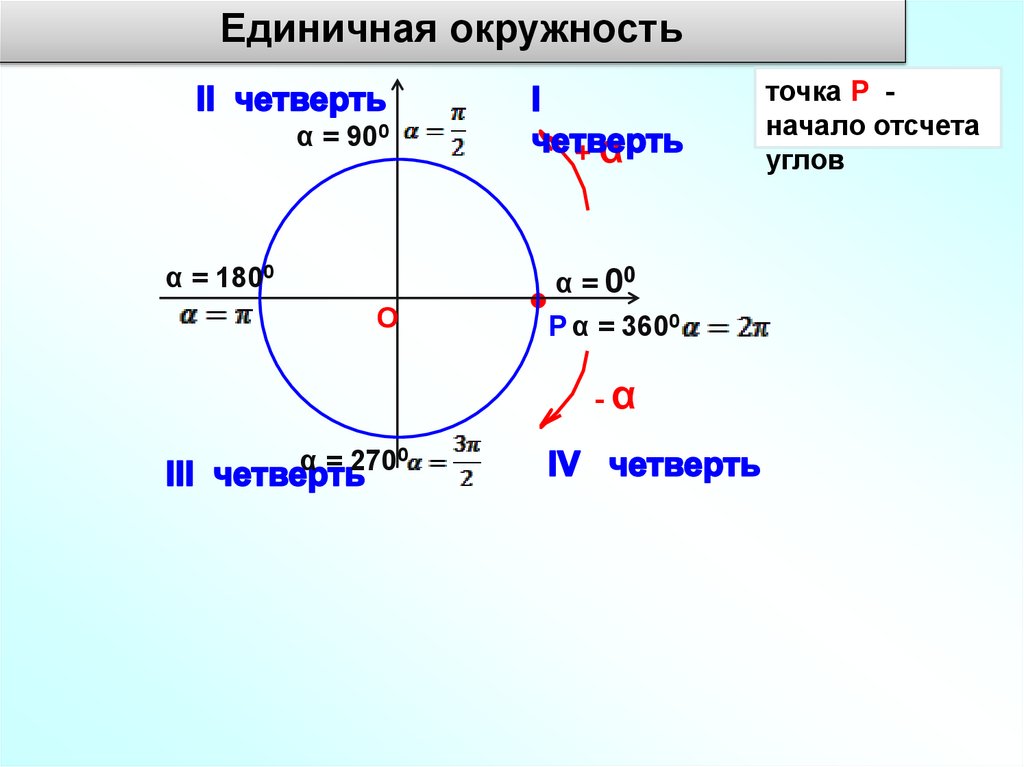
Единичная окружность
α = 900
α = 1800
+α
α = 00
О
Р α = 3600
-α
α = 2700
точка Р начало отсчета
углов

13.

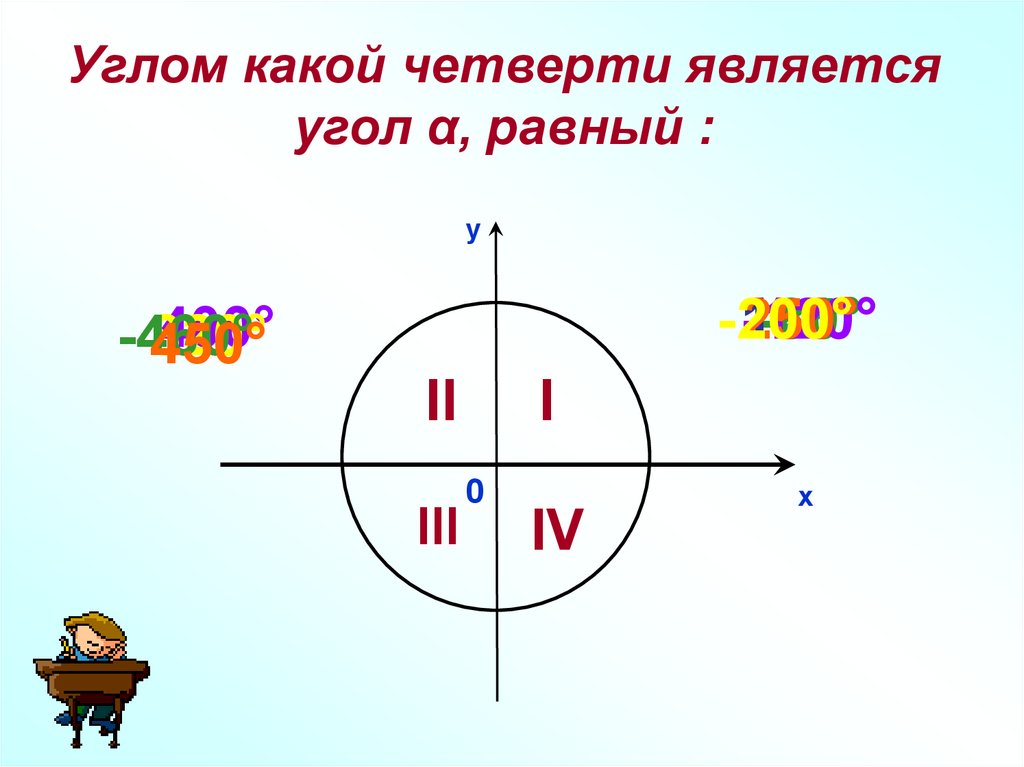
Углом какой четверти является
угол α, равный :
у
-200°
250°
-120°
150°
-80°
45°
400°
-460°
820°
450°
II
III
I
0
IV
х

14.

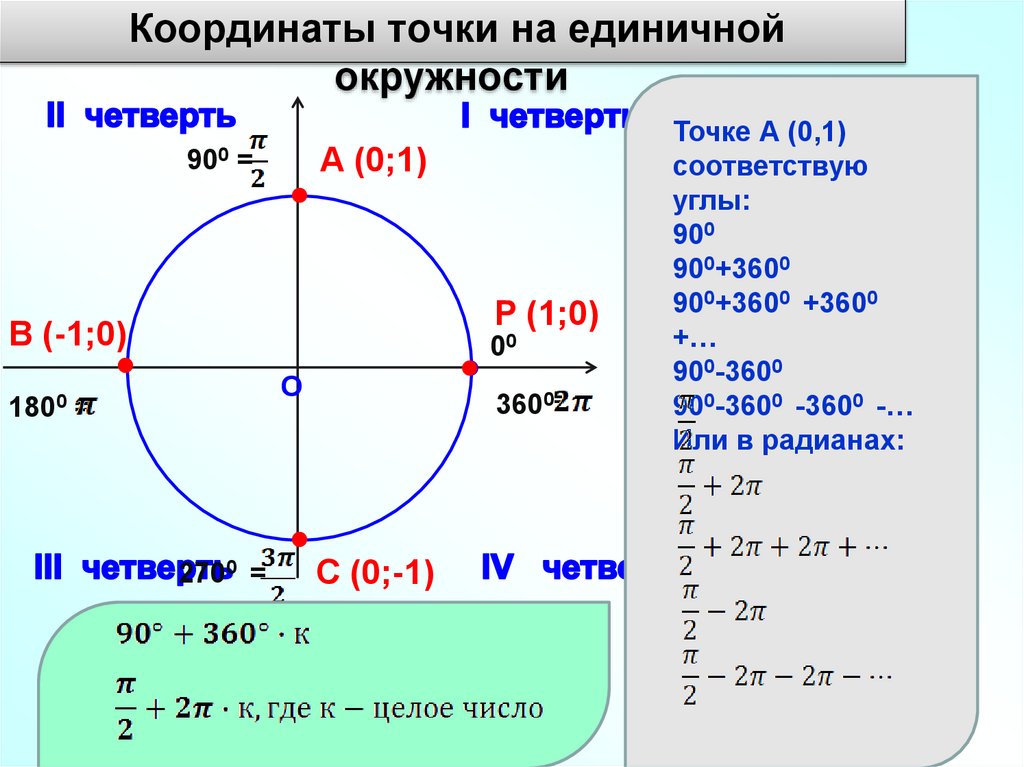
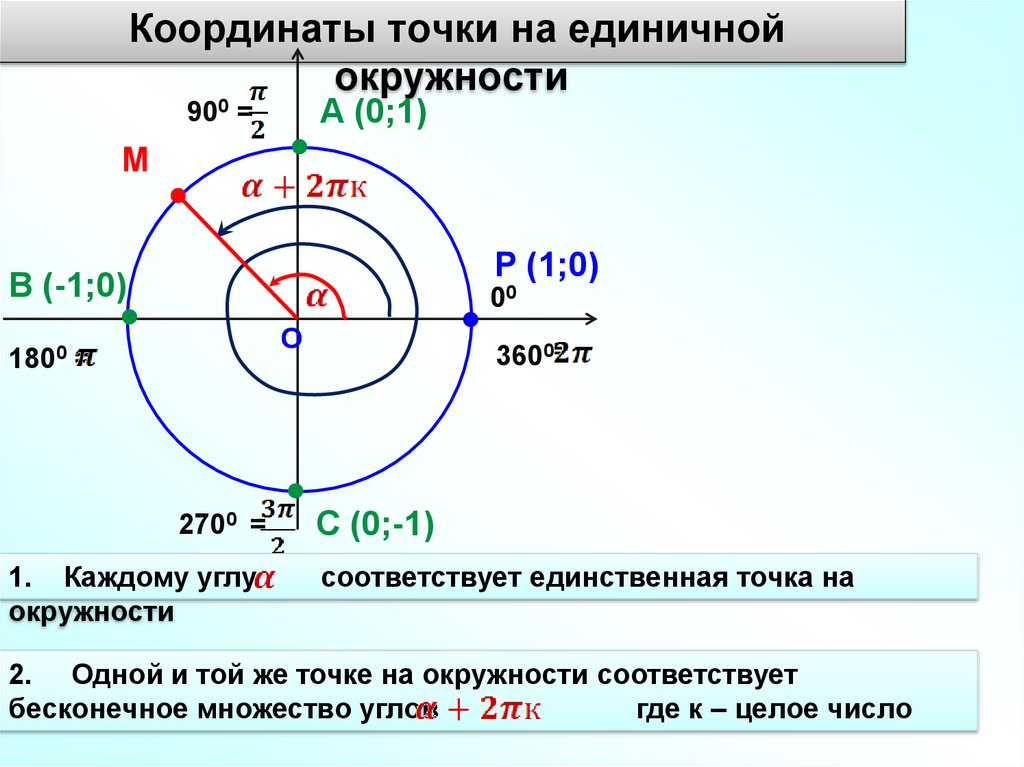
Координаты точки на единичной
окружности
А (0;1)
900 =
Р (1;0)
В (-1;0)
00
О
1800 =
2700 =
3600=
С (0;-1)
Точке А (0,1)
соответствую
углы:
900
900+3600
900+3600 +3600
+…
900-3600
900-3600 -3600 -…
Или в радианах:

15.

Координаты точки на единичной
окружности
А (0;1)
900 =
М
Р (1;0)
В (-1;0)
00
О
1800 =
2700 =
1. Каждому углу
окружности
3600=
С (0;-1)
соответствует единственная точка на
2. Одной и той же точке на окружности соответствует
бесконечное множество углов
где к – целое число

16.

17.

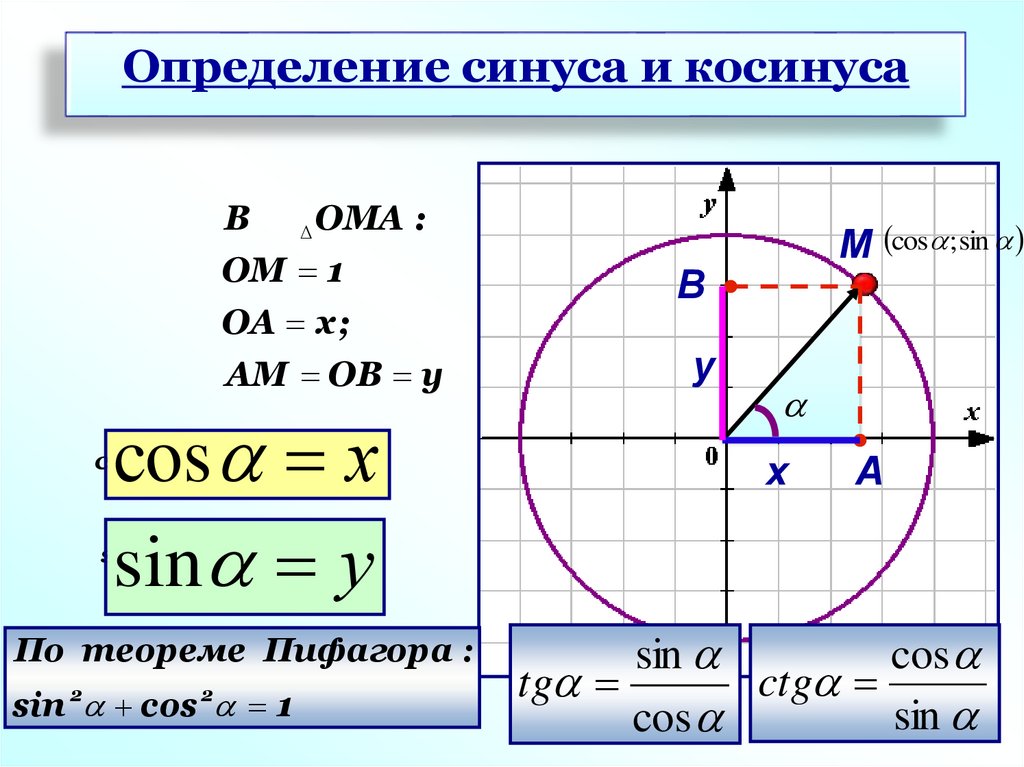
Определение синуса и косинуса
B
Δ
ОМА :
ОМ 1
ОА х;
АМ ОВ у
cos х
sin у
cos
OА х
х
OМ 1
sin
AМ у
у
OМ 1
По теореме Пифагора :
sin 2 cos 2 1
M cos ; sin
B
y
x
A
cos
sin
ctg
tg
sin
cos

18.

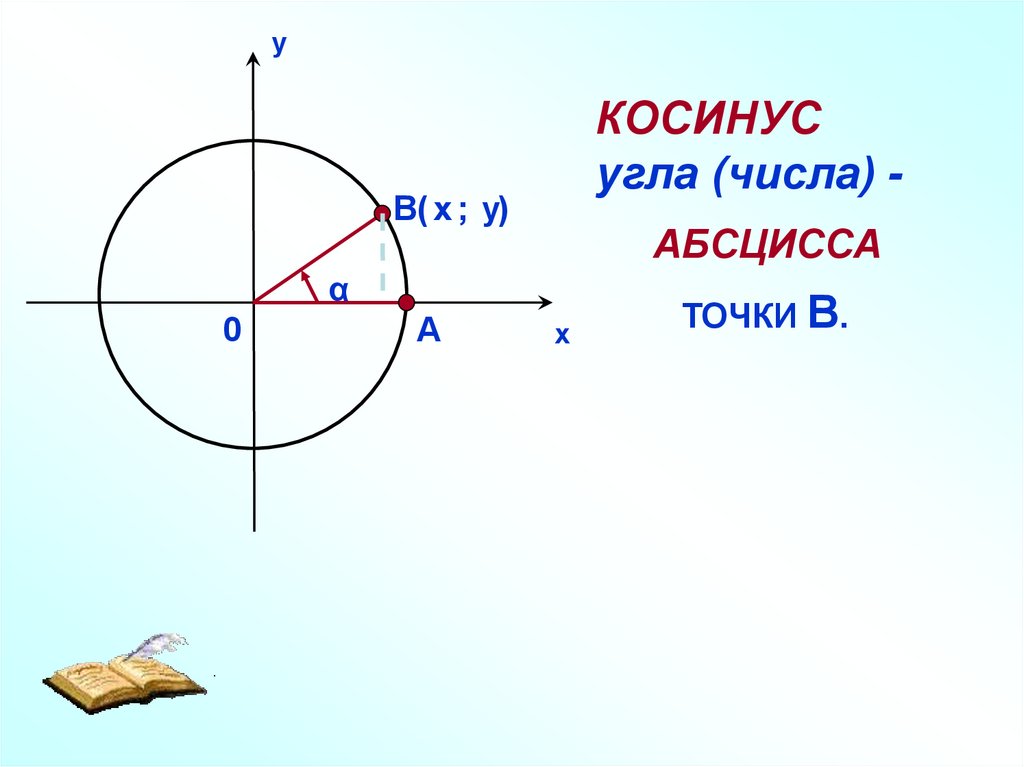
у
КОСИНУС
угла (числа) -
В( х ; у)
АБСЦИССА
α
0
А
х
ТОЧКИ В.

19.

у
СИНУС угла
(числа) В( х ; у )
ОРДИНАТА
α
0
А
х
ТОЧКИ В.

20.

cos
cos
cos
cos
180
270
90
0000===10
–1
0
sin
sin
sin
sin
270
180
90
00000===0–1
10
y
1
π
—
90o 2
(0;1)
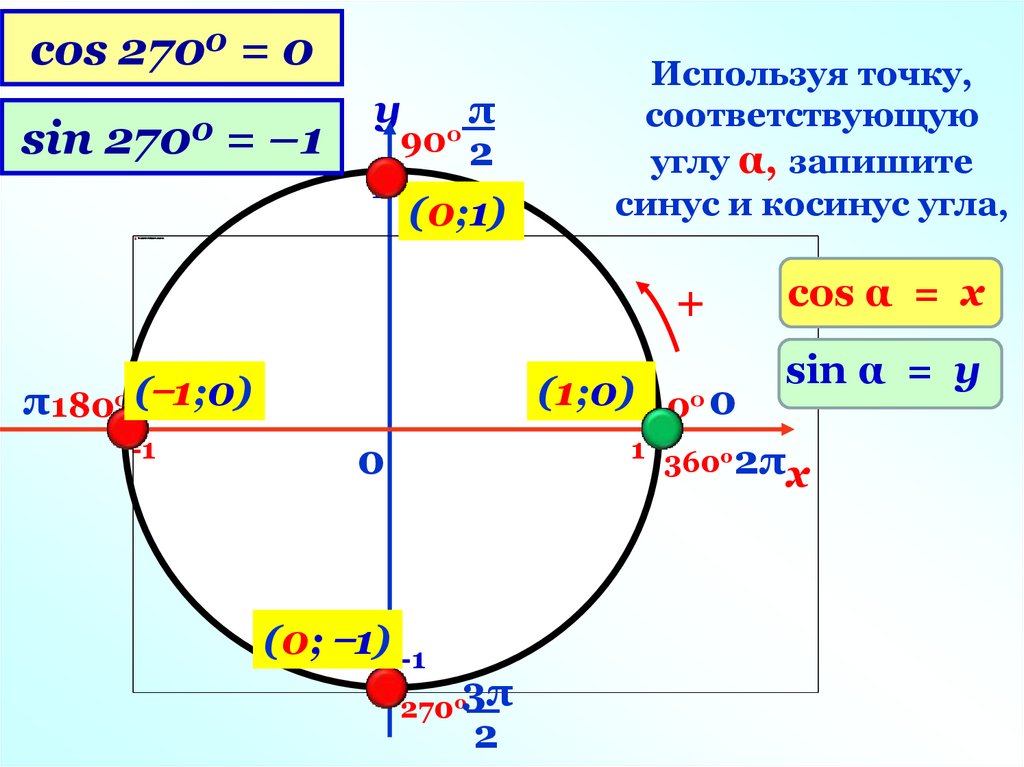
Используя точку,
соответствующую
углу α, запишите
синус и косинус угла,
+
sin α = у
π180o ( ̶ 1;0)
-1
cos α = x
(1;0) 0o 0
1 360o
2πx
0
(0; ̶ 1) -1
270o3π
—
2

21.

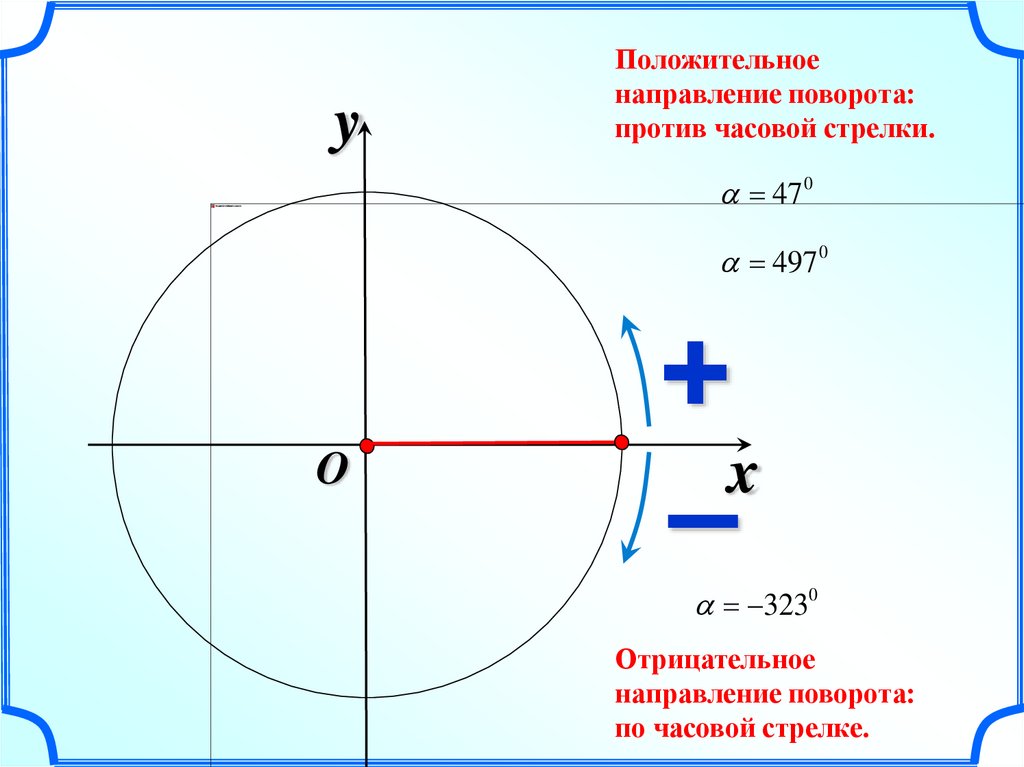
y
Положительное
направление поворота:
против часовой стрелки.
47 0
497 0
O
+
x
–
3230
Отрицательное
направление поворота:
по часовой стрелке.

22.

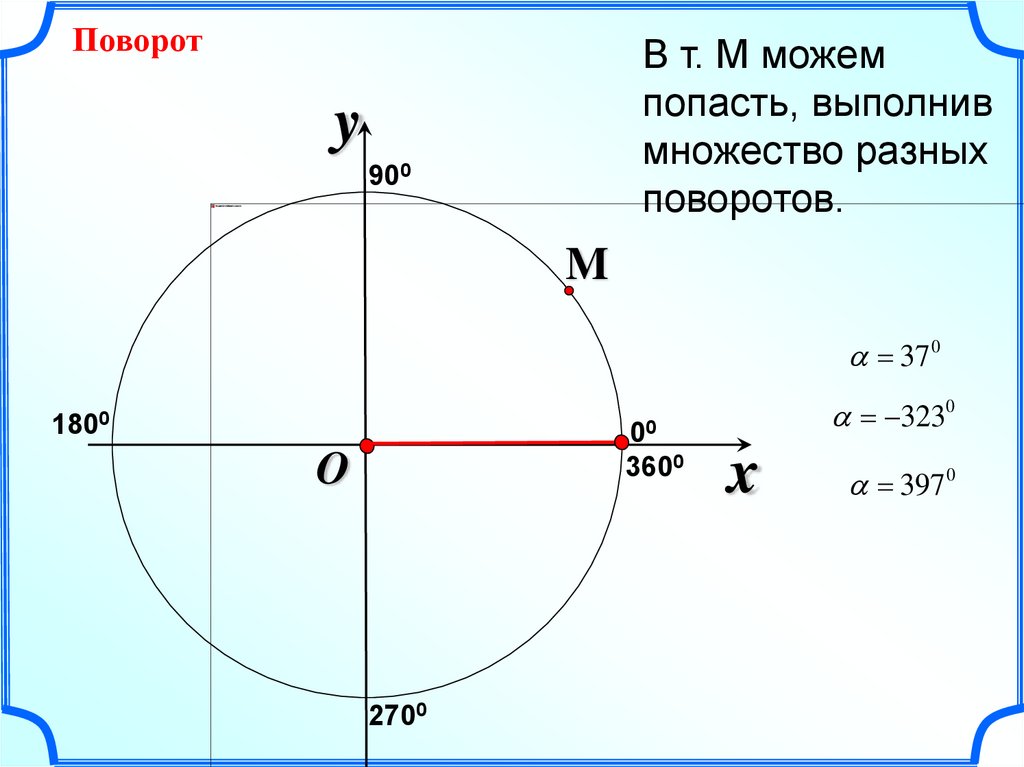
Поворот
В т. М можем
попасть, выполнив
множество разных
поворотов.
y
900
M
37 0
1800
00
3600
O
2700
3230
x
397 0

23.

называется ордината y точки М, а
косинусом угла – абсцисса x точки М.
Cинусом угла
sin a = y; cos a = x
sin
tg
cos
cos
ctg
sin
sin cos
1
tg ctg
cos sin

24.

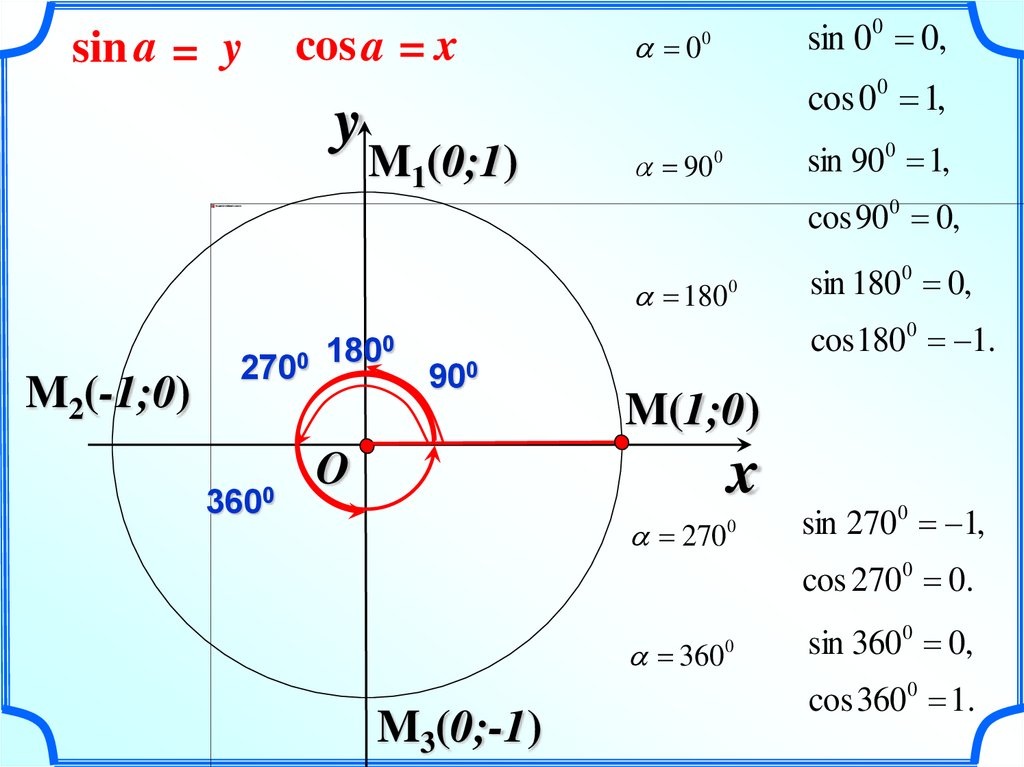
sin a = y
cos a = x
y
0
sin 00 0,
0
cos 00 1,
M1(0;1)
90
sin 900 1,
0
cos 900 0,
180
M2(-1;0)
2700
3600
1800
0
sin 1800 0,
cos1800 1.
900
M(1;0)
x
O
270
0
sin 2700 1,
cos 2700 0.
360
M3(0;-1)
0
sin 3600 0,
cos 3600 1.

25.

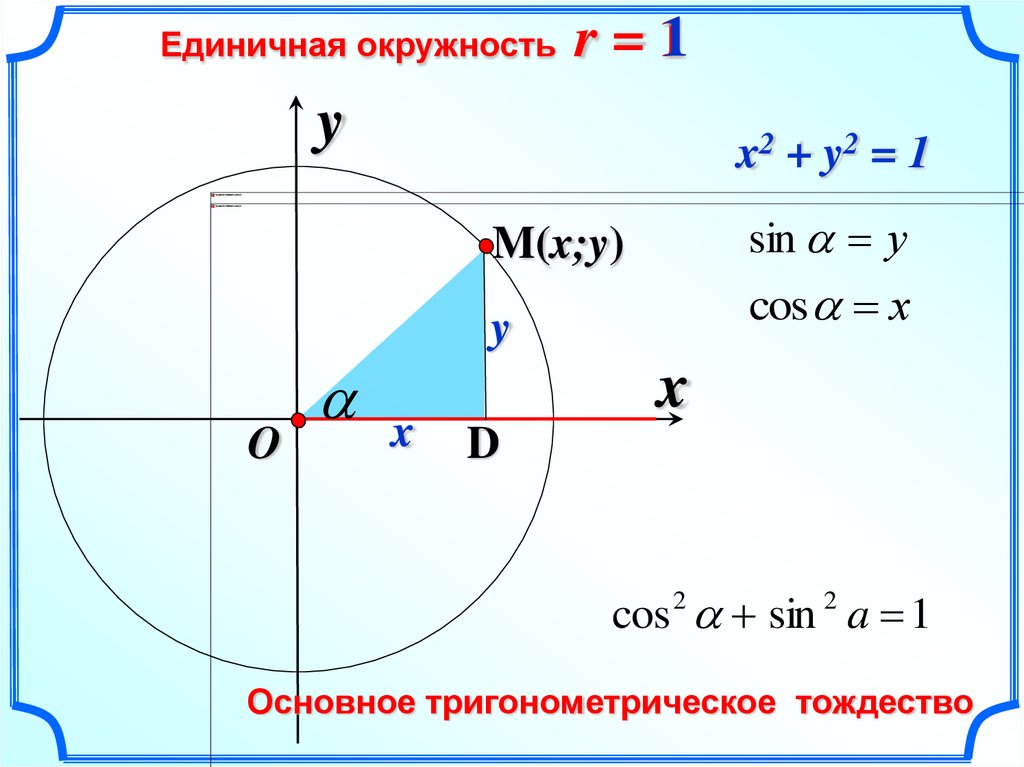
Единичная окружность
r=1
y
x2 + y2 = 1
sin у
M(x;y)
cos х
y
O
x
x
D
cos sin a 1
2
2
Основное тригонометрическое тождество

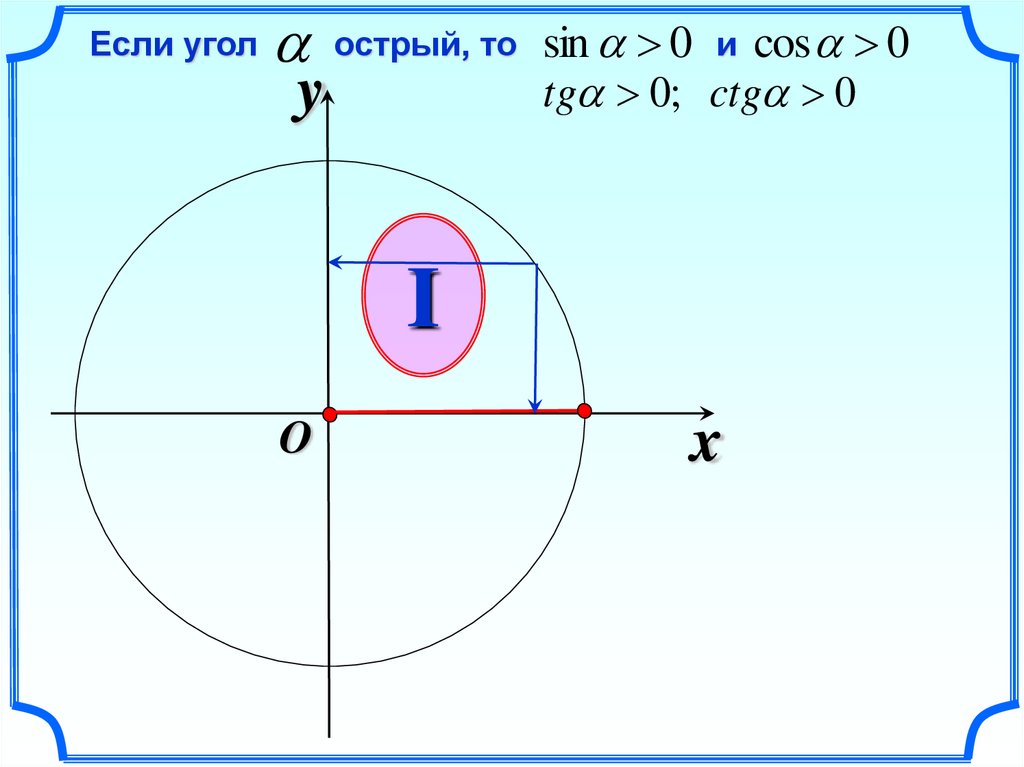
26.

Если угол
острый, то sin 0 и cos 0
tg 0; ctg 0
y
I
O
x

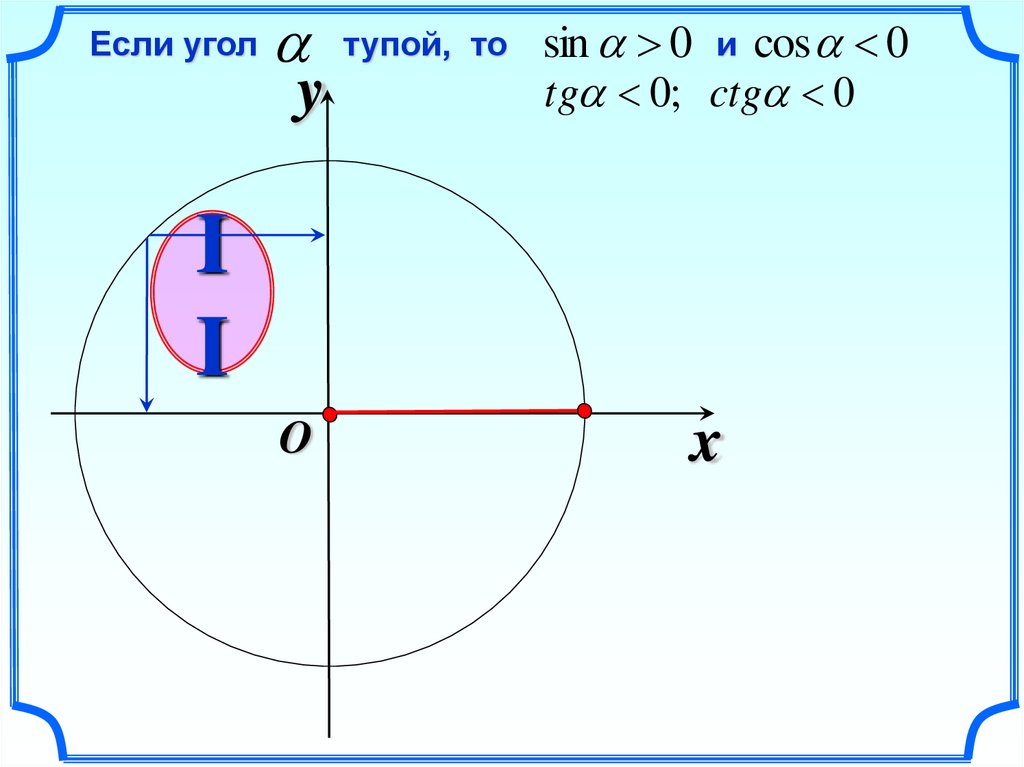
27.

Если угол
тупой, то sin 0 и cos 0
tg 0; ctg 0
y
I
I
O
x

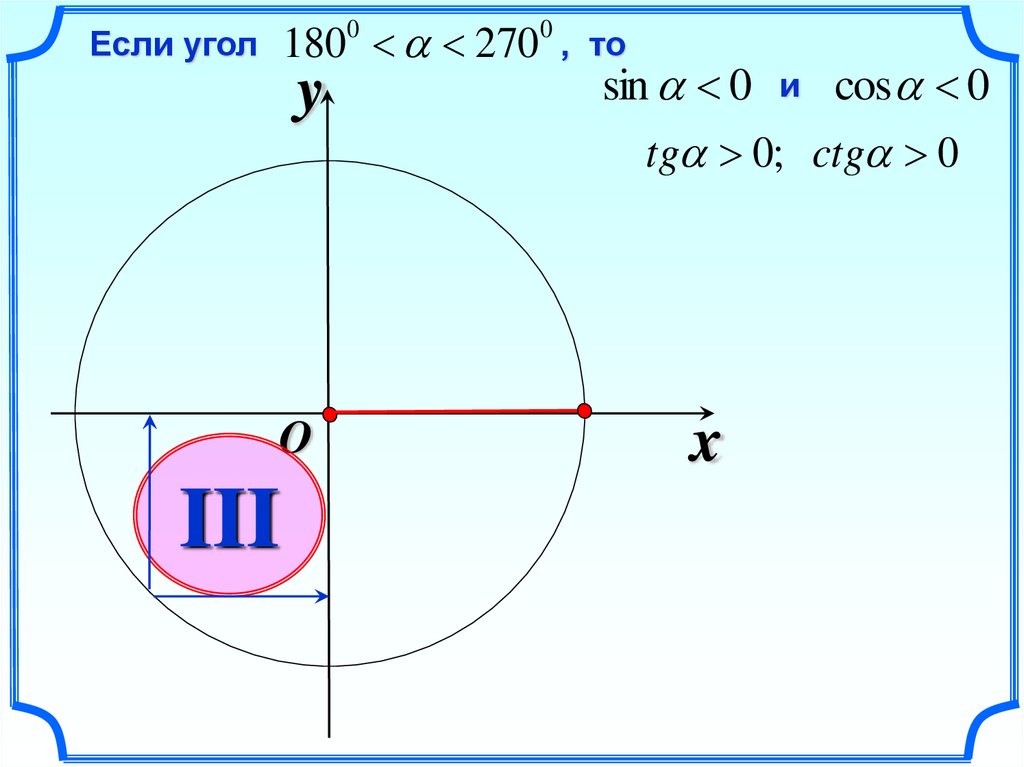
28.

180 270 , то
sin 0 и cos 0
y
0
Если угол
0
tg 0; ctg 0
O
III
x

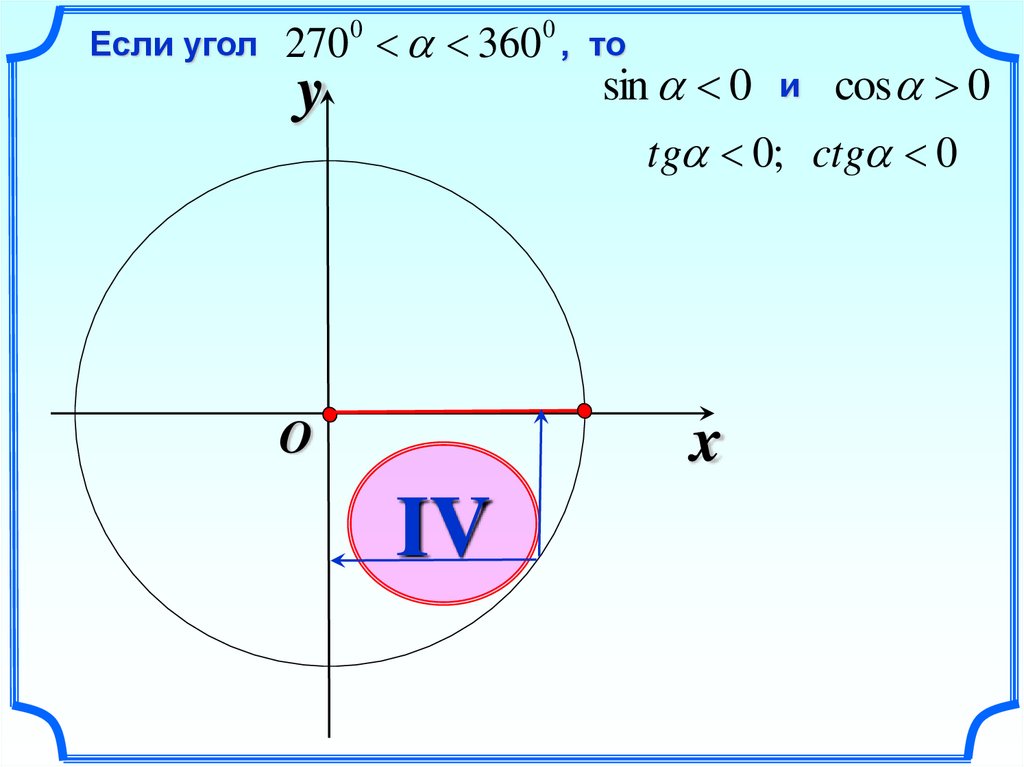
29.

Если угол
270 360 , то
sin 0 и cos 0
y
0
0
tg 0; ctg 0
x
O
IV

30.

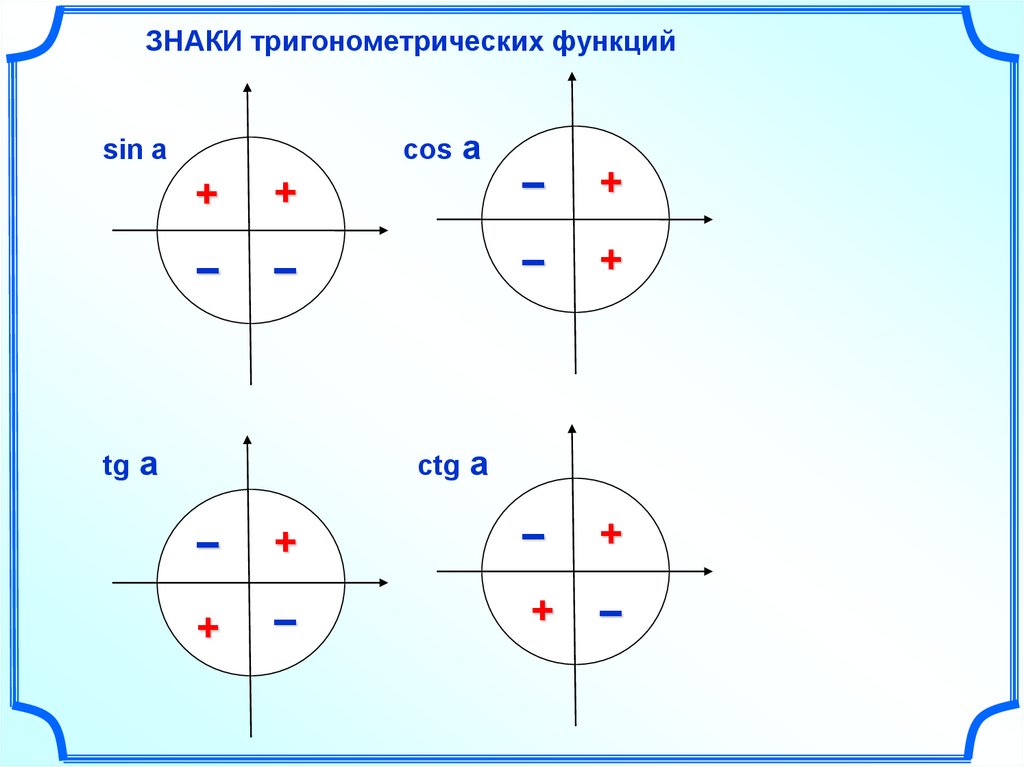
ЗНАКИ тригонометрических функций
cos a
sin a
+
+
–
+
–
–
–
+
tg a
ctg a
–
+
–
+
+
–
+
–

31.

Определить знак выражения .
cos 275 sin 205
tg 200 ctg105
275 4 четверть
200О 3 четверть
cos 275 0
tg 2000 0
205 3 четверть
105О 2 четверть
sin 205 0
ctg1050 0
О
0
О
0
cos 275 sin 205
0
tg 200 ctg105

32.

Определить знак выражения .
cos 25 sin 95
tg 280 ctg195
25 1 четверть
280О 4 четверть
cos 25 0
tg 2800 0
95 2 четверть
195О 3 четверть
sin 95 0
ctg1950 0
О
0
О
0
cos 25 sin 95
0
tg 280 ctg195

33.

34.

Вычислить:
3
sin 3 cos
0-0=0
2
sin cos 2 0+1=1
tg cos 0+0=0
sin
4
cos
4
sin
3
cos
6
2 3
1
4 4
4
2
2
3
3
2
2
2
2

35.

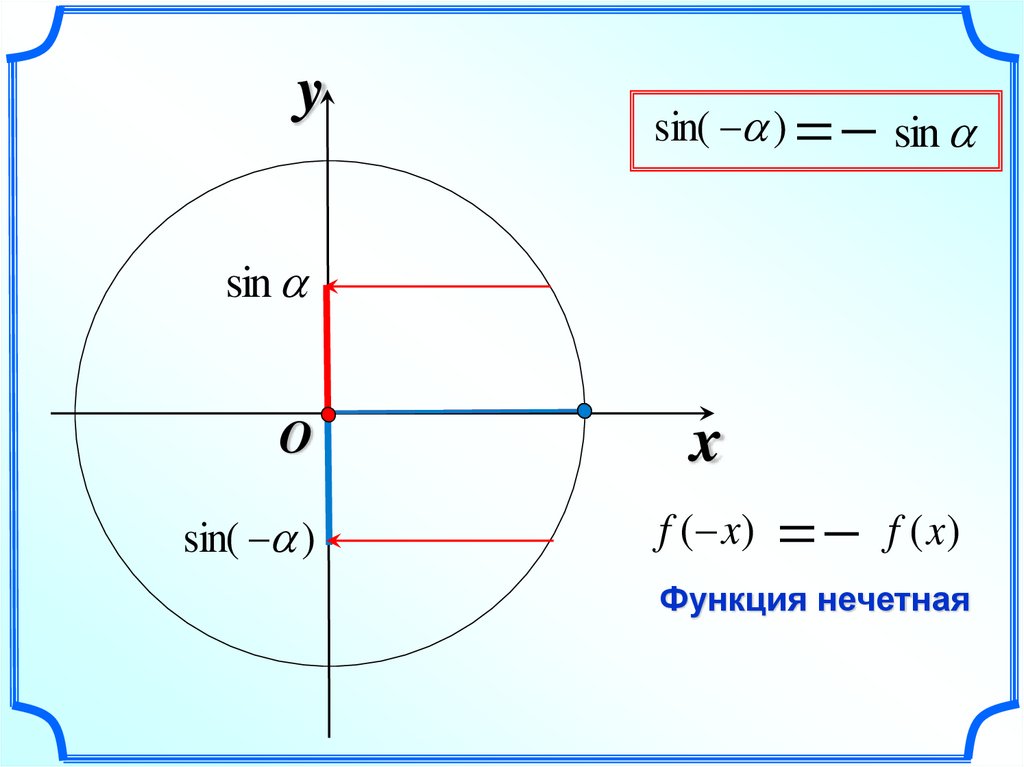
y
sin( ) sin
sin
O
sin( )
x
f ( x) f (x)
Функция нечетная

36.

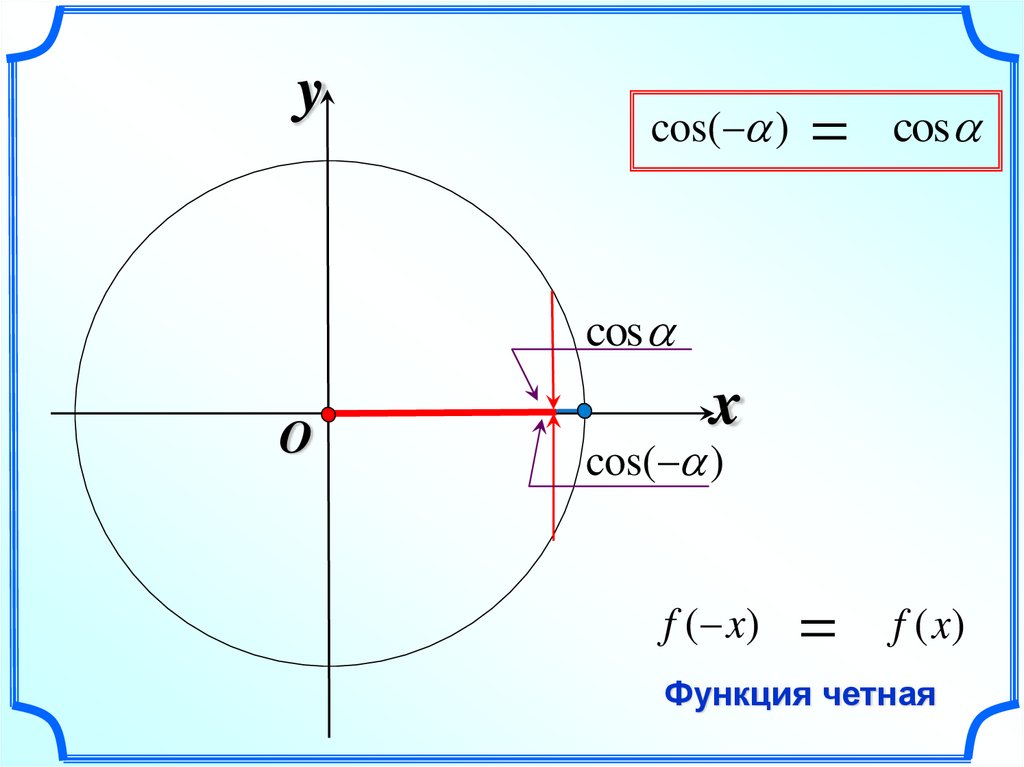
y
cos( )
cos
cos
O
x
cos( )
f ( x)
f (x)
Функция четная

37.

sin
tg
cos
sin
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x) f (x)
Функция нечетная
Докажи самостоятельно
tg( ) tg
ctg( ) ctg

38.

f ( x)
f (x)
f ( x) f (x)
Функция четная
Функция нечетная
cos( )
sin( ) sin
cos
tg( ) tg
ctg( ) ctg

39.

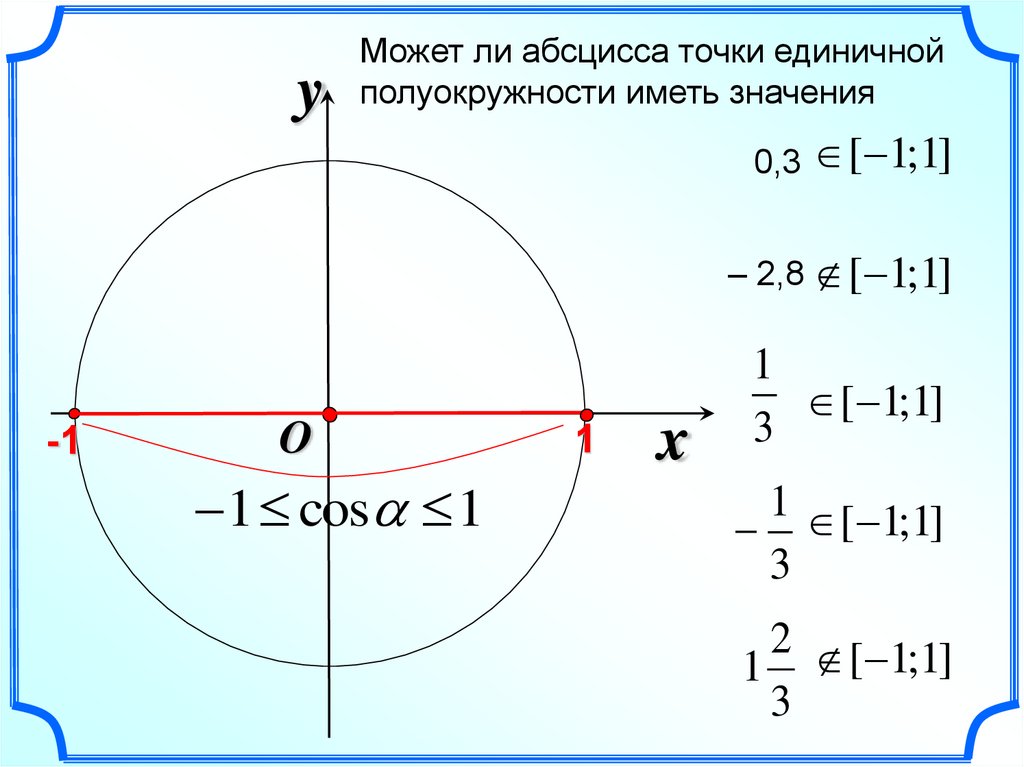
y
Может ли абсцисса точки единичной
полуокружности иметь значения
0,3 [ 1;1]
– 2,8 [ 1;1]
-1
O
1 cos 1
1
x
1
[ 1;1]
3
1 [ 1;1]
3
2 [ 1;1]
1
3

40.

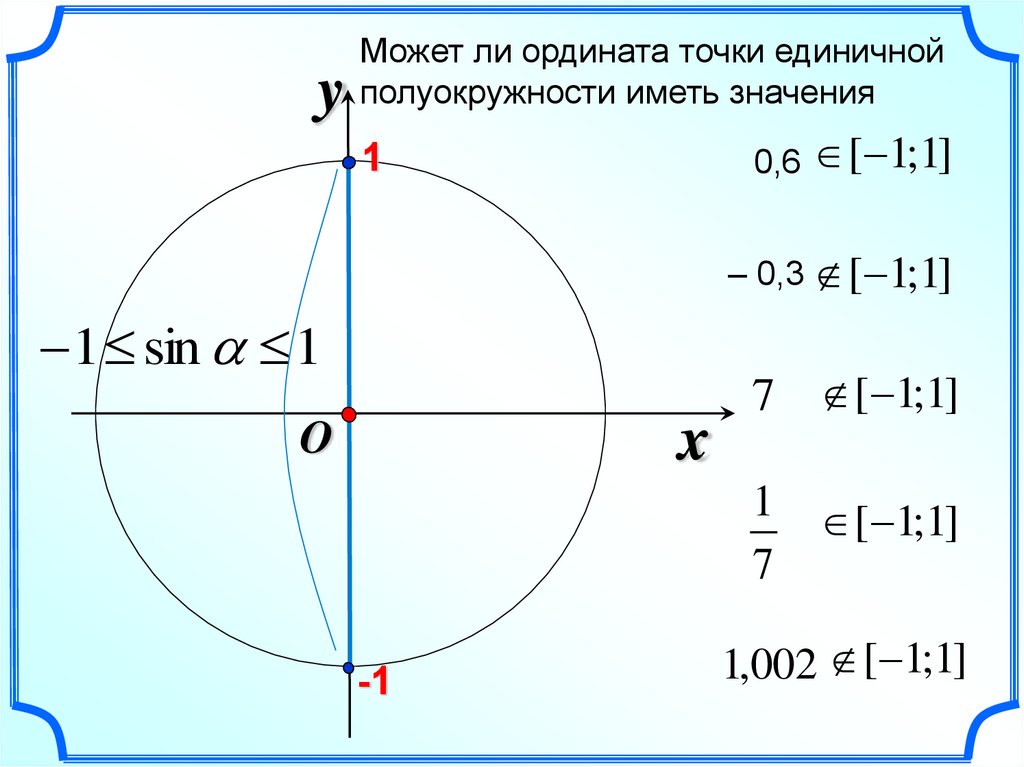
y
Может ли ордината точки единичной
полуокружности иметь значения
0,6 [ 1;1]
1
– 0,3 [ 1;1]
1 sin 1
x
O
7 [ 1;1]
1
7
-1
[ 1;1]
1,002 [ 1;1]

41.

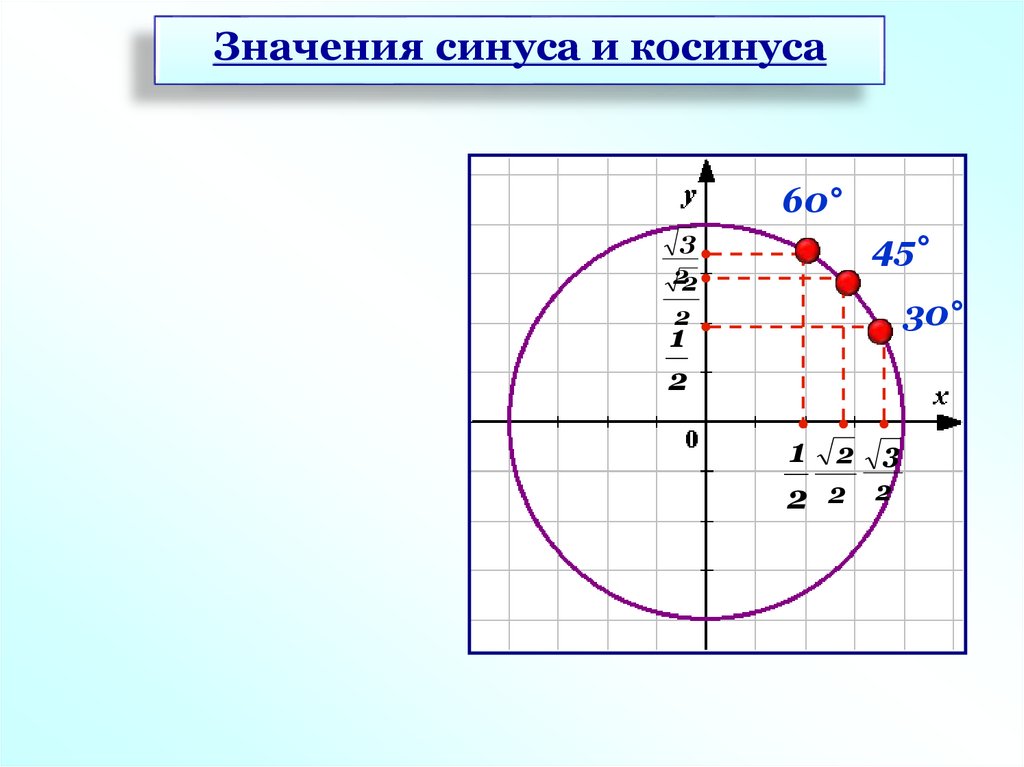
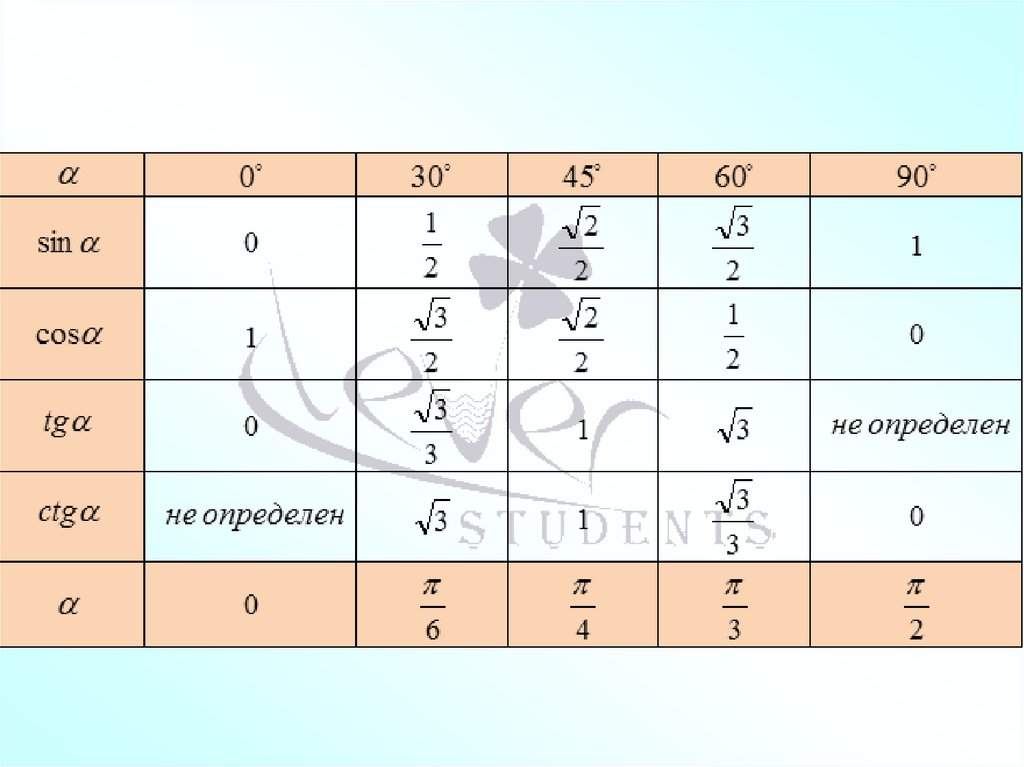
Значения синуса и косинуса
60°
3
22
45°
30°
2
1
2
1 2 3
2 2 2

42.

43.

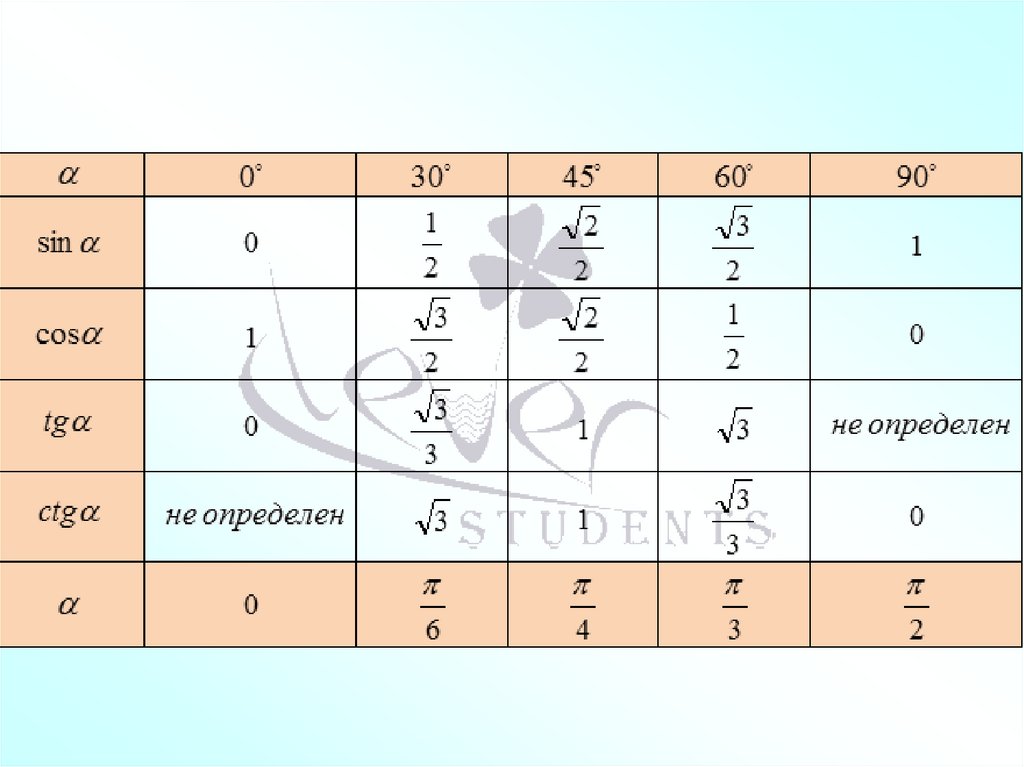
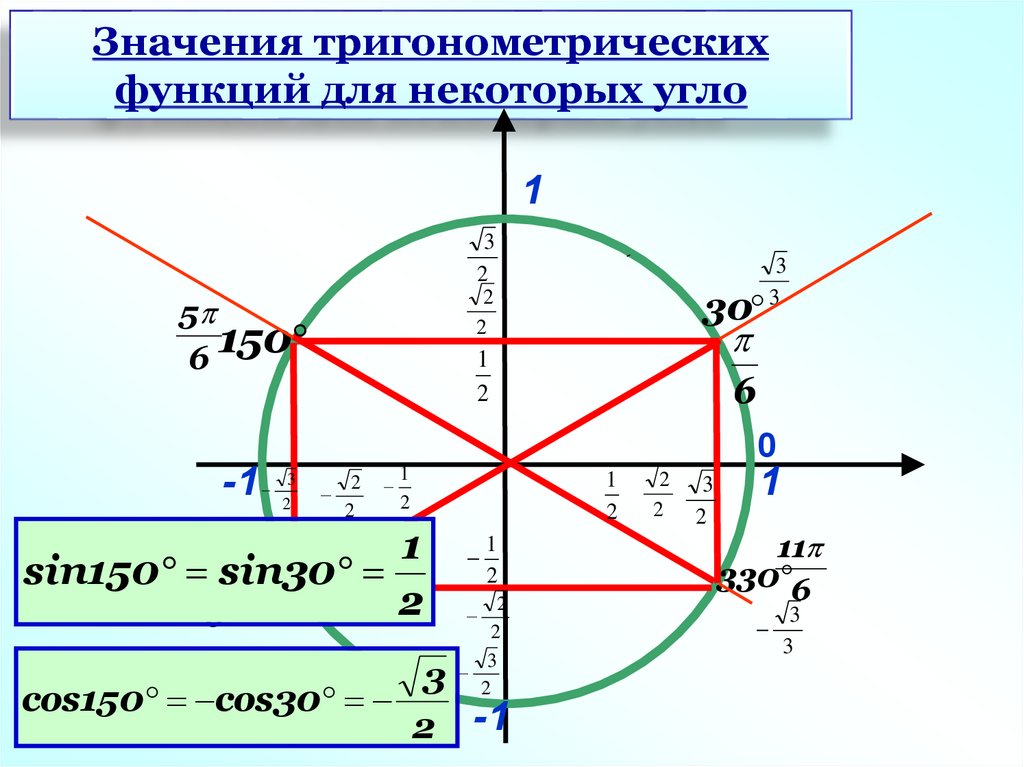
Значения тригонометрических
функций для некоторых угло
1
3
2
5
150
6
2
2
30
1
2
6
3
3
0
-1 23 2 12
1
2
2
1
sin150 7 sin30
2
6 210
1
2
2
2
3
2
3
cos150 cos30
2 -1
2
2
3
2
1
11
330 6
3
3

44.

45.

Вычислить:
sin
2
cos
4
3
1 1
0
2 2
tg
6
2
2 1
2 2
cos 2
3 3
3
1
3
3
1 2
tg cos sin cos 1 0
2 2
4
2
6
4
2
4