Похожие презентации:
Определение синуса, косинуса, тангенса и котангенса угла
1.
2.
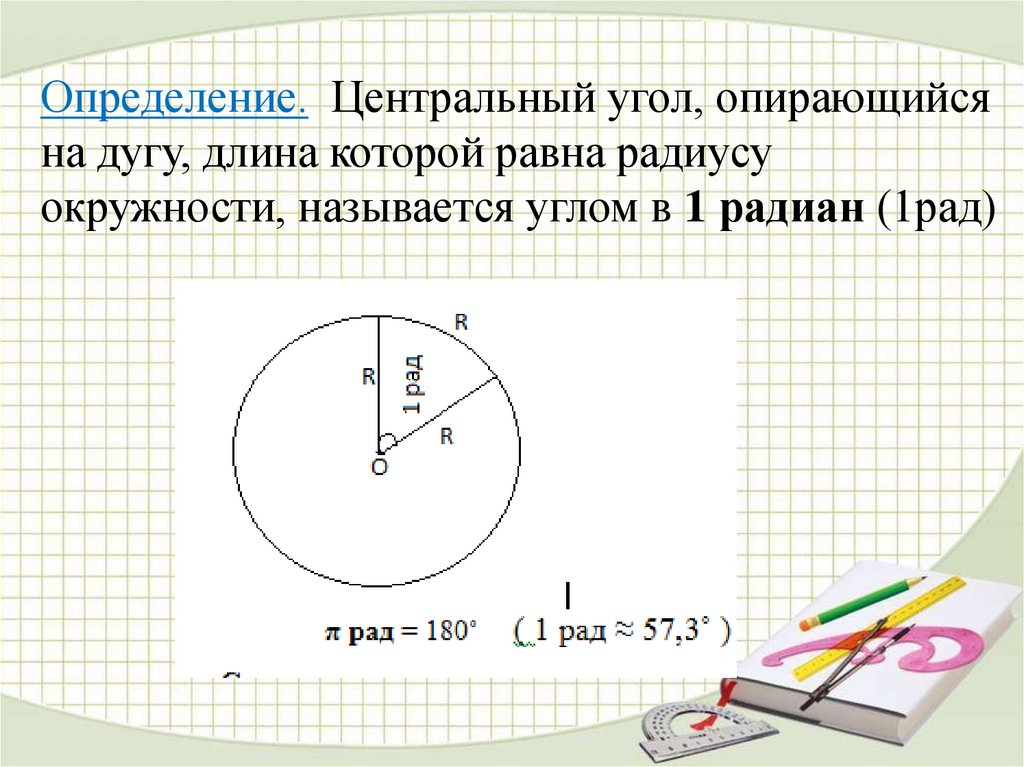
Определение. Центральный угол, опирающийсяна дугу, длина которой равна радиусу
окружности, называется углом в 1 радиан (1рад)
3.
4.
5.
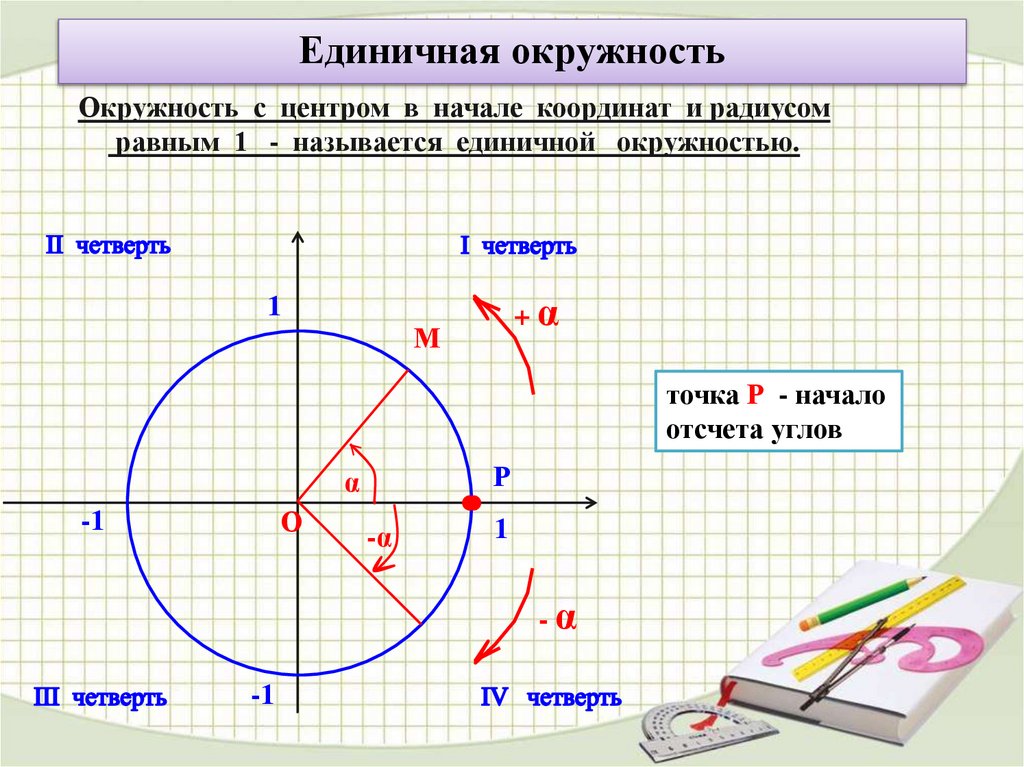
Единичная окружностьОкружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
+α
1
М
точка Р - начало
отсчета углов
Р
α
О
-1
-α
1
-α
-1
6.
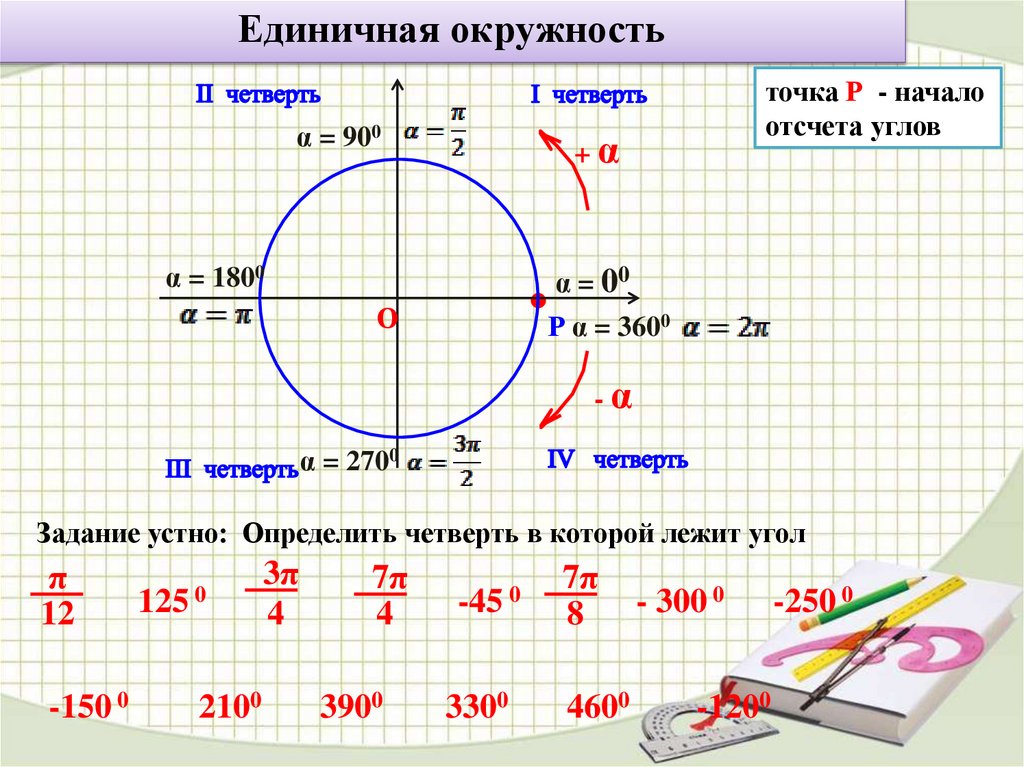
Единичная окружностьα = 900
точка Р - начало
отсчета углов
+α
α = 1800
α = 00
О
Р α = 3600
-α
α = 2700
Задание устно: Определить четверть в которой лежит угол
π
12
-150 0
125 0
2100
3π
4
7π
4
3900
-45 0
7π
8
3300
4600
- 300 0
-1200
-250 0
7.
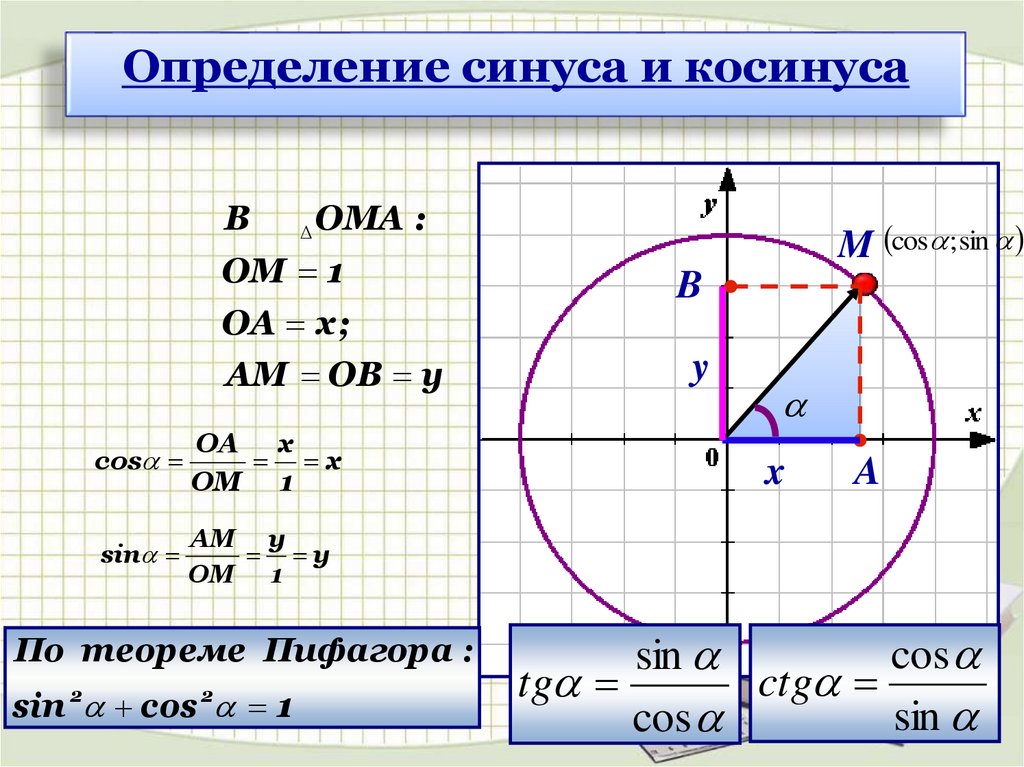
Определение синуса и косинусаB
Δ
ОМА :
ОМ 1
ОА х;
АМ ОВ у
cos
OА х
х
OМ 1
sin
AМ у
у
OМ 1
По теореме Пифагора :
sin 2 cos 2 1
M cos ; sin
B
y
x
A
cos
sin
ctg
tg
sin
cos
8.
уО 1
с
ь
-1
с
и
н
у
с
о
в
М (x; y)
+
α
1 М (1;0)
0
Ось косинусов
̶1
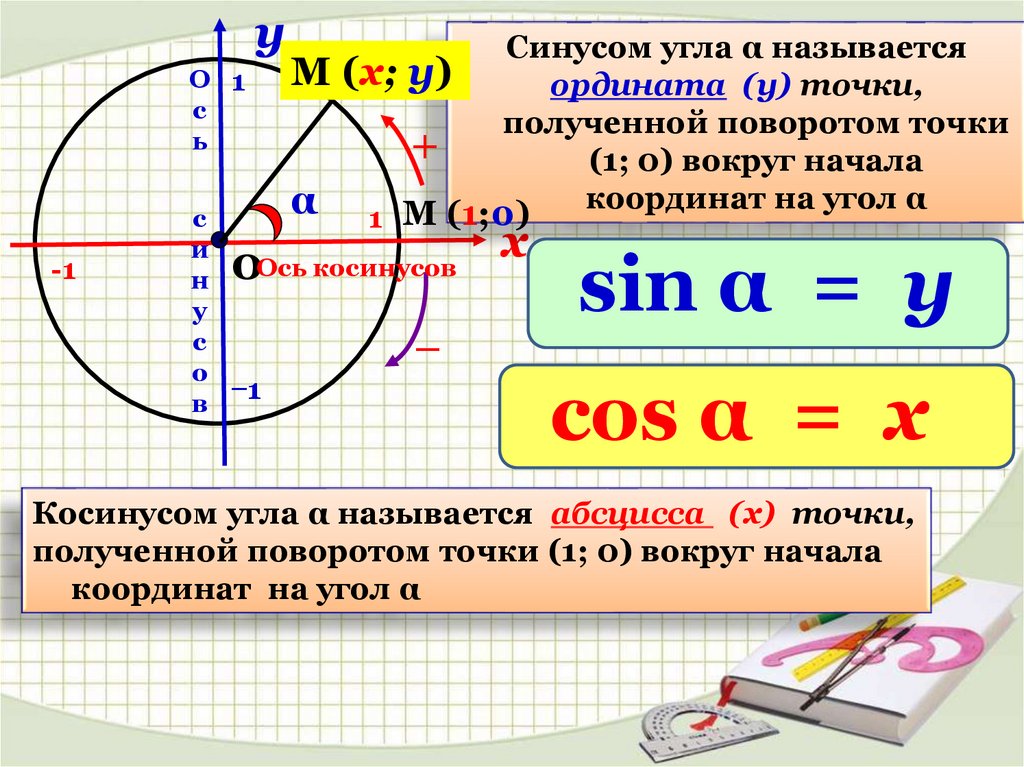
Синусом угла α называется
ордината (у) точки,
полученной поворотом точки
(1; 0) вокруг начала
координат на угол α
̶
х
sin α = у
cos α = x
Косинусом угла α называется абсцисса (х) точки,
полученной поворотом точки (1; 0) вокруг начала
координат на угол α
9.
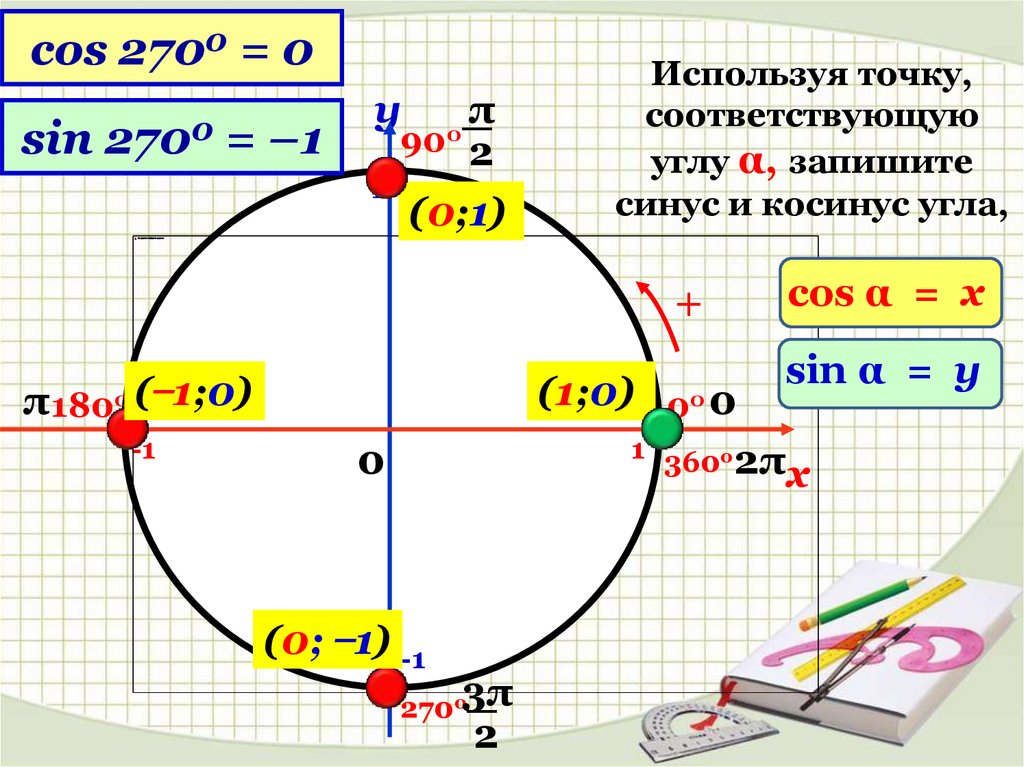
coscos
cos
cos
180
270
90
0000===10
–1
0
sin
sin
sin
sin
270
180
90
00000===0–1
10
y
1
π
—
90o 2
(0;1)
Используя точку,
соответствующую
углу α, запишите
синус и косинус угла,
+
sin α = у
π180o ( ̶ 1;0)
-1
cos α = x
(1;0) 0o 0
1 360o
2πx
0
(0; ̶ 1) -1
270o3π
—
2
10.
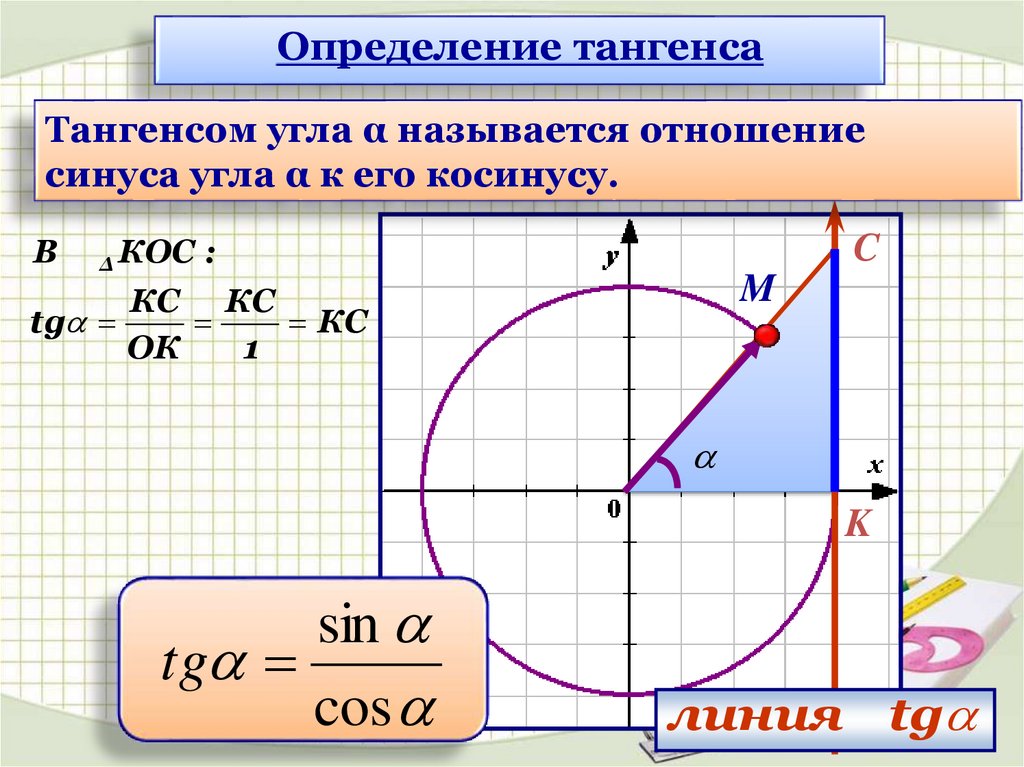
Определение тангенсаТангенсом угла α называется отношение
синуса угла α к его косинусу.
В
Δ
КОС :
C
M
КС КС
tg
КС
ОК
1
K
sin
tg
cos
линия tg
11.
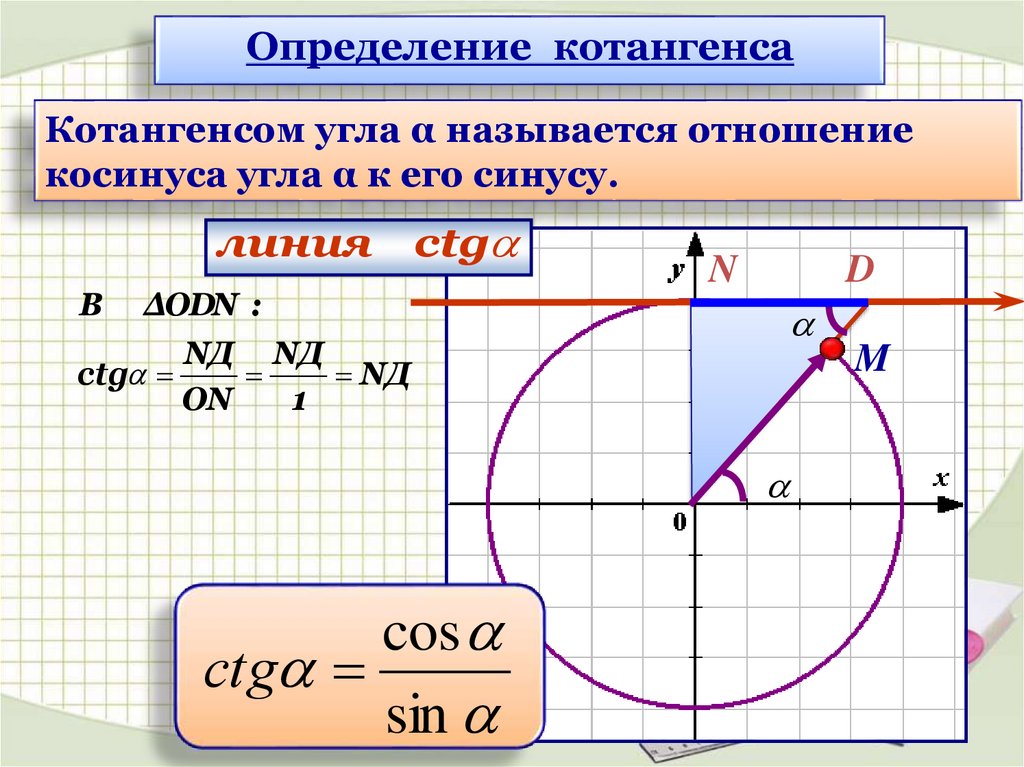
Определение котангенсаКотангенсом угла α называется отношение
косинуса угла α к его синусу.
линия сtg
В
ΔODN :
ctg
N
D
NД NД
NД
ОN
1
cos
сtg
sin
M
12.
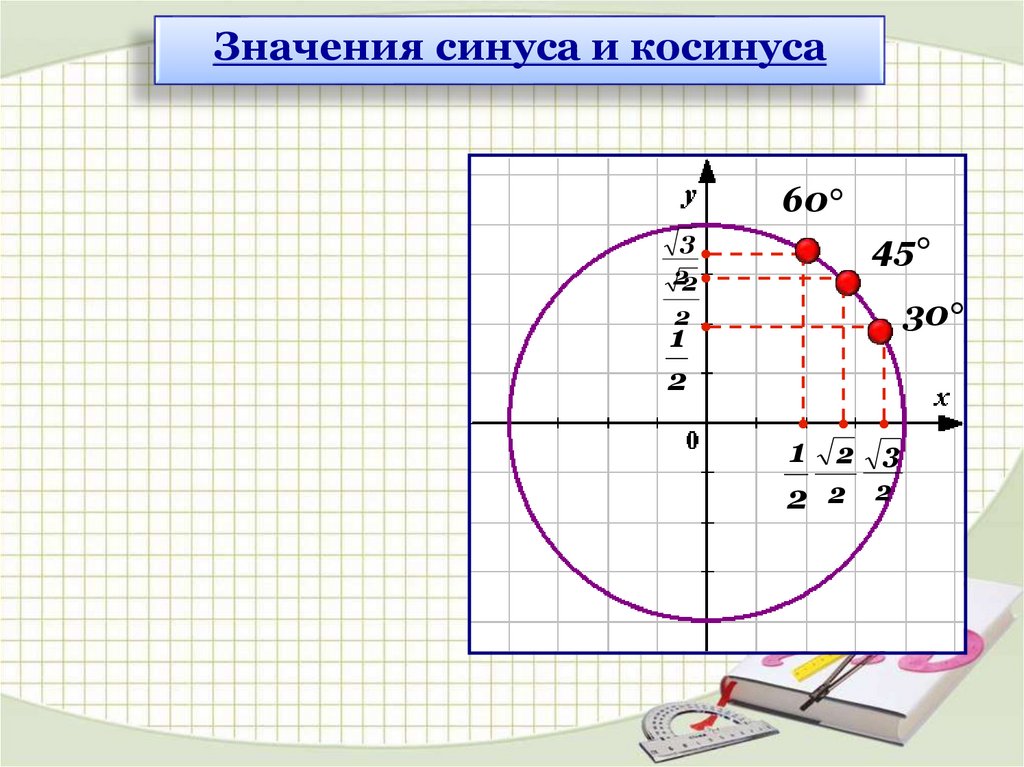
Значения синуса и косинуса60°
3
22
45°
30°
2
1
2
1 2 3
2 2 2
13.
14.
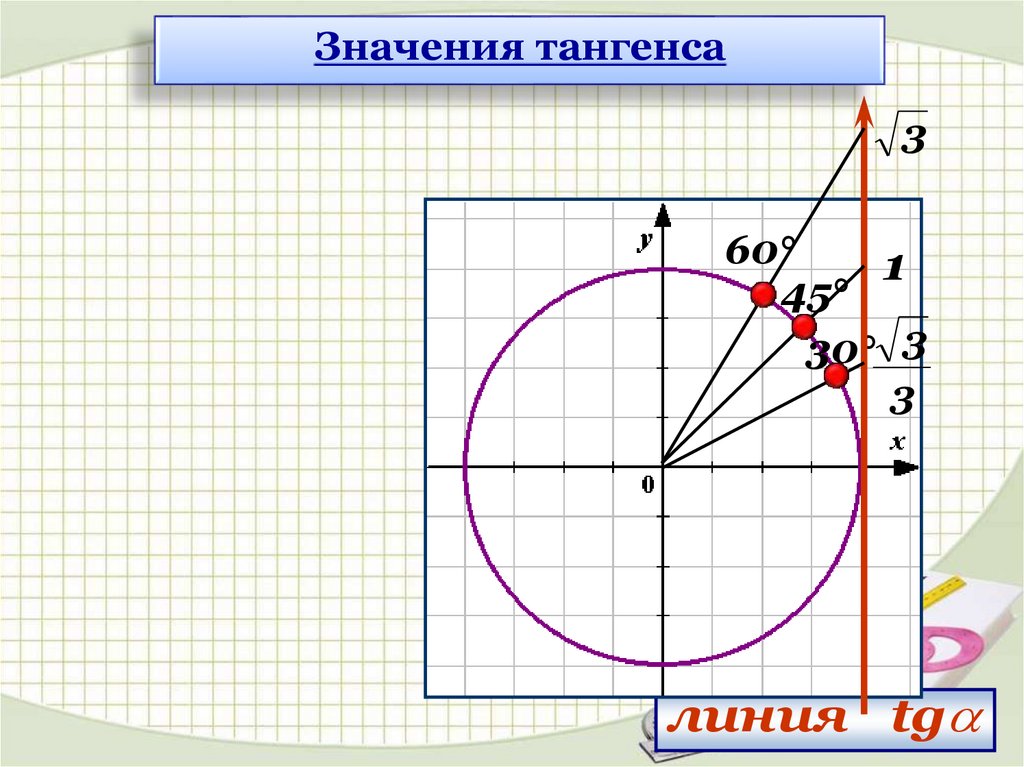
Значения тангенса3
60°
1
45°
30° 3
3
линия tg
15.
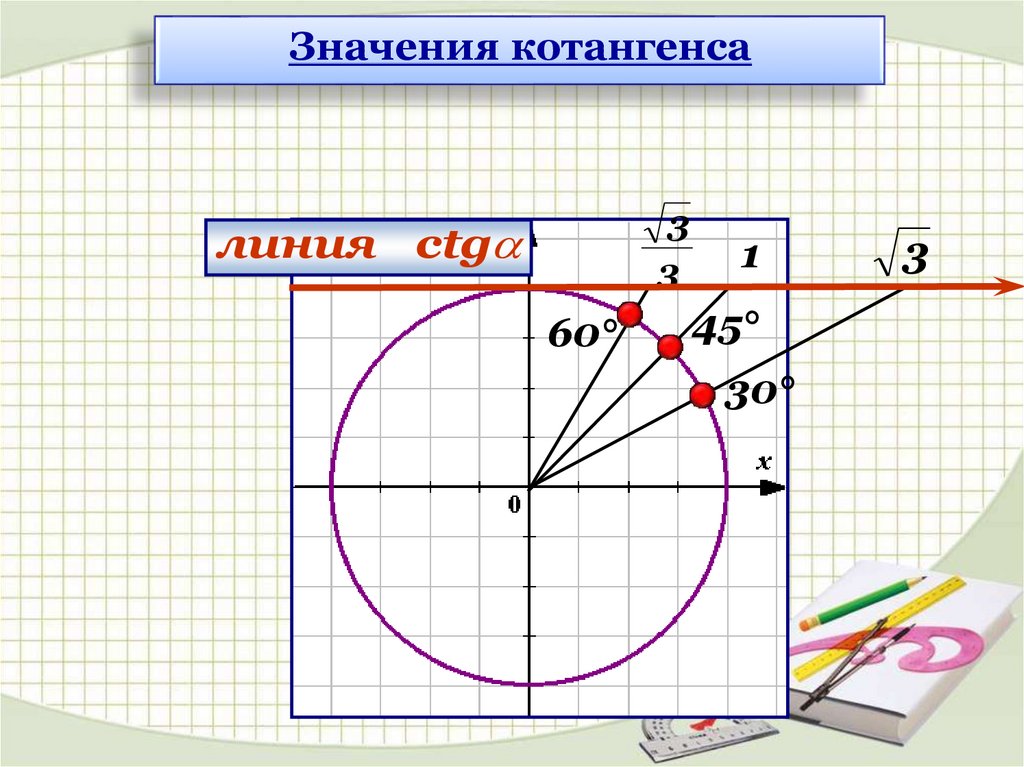
Значения котангенса3
3
линия сtg
60°
1
45°
30°
3


 Математика
Математика








