Сопротивление материалов. Курс лекций

1.

M2
z
M1
l
l

2. Лекция 8 (стр.38)

Напряжения по наклонным площадкам - Для определения напряжений по наклонной площадке,
внешняя нормаль которой повернута на угол от оси x, используем метод сечений:
σy
1. проведем наклонное сечение,
yx
y
2. отбросим правую часть,
3. заменим отброшенную часть внутренними усилиями, которые представим
в виде компонент напряжений - нормального и касательного (все напряжения
показаны положительными),
xy
z
yx
у
σx
xy
dy
dy
cos
n
σ
σx
4. составим уравнения равновесия для равнодействующих напряжений в проекциях
на нормаль к наклонному сечению и ось, касательную к сечению:
σy
t
dy
( n) :
dz x (dydz ) cos y (( dy tg )dz ) sin yx (dy tg dz ) cos xy (dydz ) sin 0,
cos
dy
(t ) :
dz x (dydz ) sin y (( dy tg )dz ) cos s yx (dy tg dz ) sin xy (dydz ) cos 0.
cos
xy
yx
x dz
σx
dy.tg
x
σy
После деления уравнений на dydz, умножения на cos , подстановки закона парности касательных напряжений и переноса в правую часть получим:
x cos 2 y sin 2 2 yx sin cos ,
x cos 2 y sin 2 yx sin 2 ,
Или используя известные
тригонометрические
формулы двойного угла:
x sin cos y sin cos yx (sin 2 cos2 ).
Получены формулы для определения напряжений в любых площадках, проходящих через данную
точку, если известны напряжения x, y и yx = - xy. Определим, каковы будут напряжения на
площадке, перпендикулярной к рассмотренной наклонной площадке:
x y
2
sin 2 yx cos 2
90 x cos 2 ( 900 ) y sin 2 ( 900 ) yx sin 2( 900 ) x sin 2 y cos 2 yx sin 2 .
y
x y
90 x
sin 2( 900 ) yx cos 2( 900 )
sin 2 yx cos 2
0
0
2
2
Из сравнения выражений для касательных напряжений вновь получаем закон парности касательных напряжений:
Складывая выражения для нормальных напряжений получаем закон постоянства
суммы нормальных напряжений в любых взаимно перпендикулярных площадках:
+900 = - .
90 x y const .
0
Из постоянства суммы нормальных напряжений следует, что при повороте этих площадок приращения (изменения)
нормальных напряжений равны и противоположны по знаку:
d d
d - d
0 0;
0.
90
90
Соответственно, если на одной из площадок нормальные напряжения достигает максимума,
то на второй площадке они являются минимальными.
38

3. Лекция 8 (стр. 39)

Напряженное состояние в точке - При анализе напряжений в окрестности рассматриваемой точки выделим бесконечно малый
объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения,
например, для грани, перпендикулярной оси x (площадка x) – σx, xy, xz .
Этот элемент можно по разному ориентировать в пространстве. При поворотах элемента нормальные и касательные
yz σy
напряжения на его наклонных гранях будут принимать новые значения.
yx
Представляет интерес исследовать, как изменяются эти напряжения от изменения ориентации элемента.
y zy
Это позволит найти наклонные площадки, по которым напряжения принимают максимальные и нулевые значения.
xy
σz
Рассмотрим эту проблему вначале для более простого случая – плоского напряженного состояния.
z
zx xz σ
Плоское напряженное состояние – такое состояние, при котором две параллельные грани элемента
x
свободны от напряжений, т.е. на них отсутствуют и нормальные и касательные напряжения. Такое напряженное
состояние возникает в тонких пластинах, поверхности которых свободны от нагрузок, на незагруженной поверхности тел,
x
при изгибе балок, кручении валов.
Ниже будет показано, в этом случае напряжения zx и zу
Пусть, например, по площадкам z напряжения отсутствуют:
также должны отсутствовать.
у
yx σy
Теперь элемент можно представить в виде его проекции на плоскость x, y. На рисунке показаны
xy
положительные направления напряжений, соответствующие правилам:
σx
1.
положительные нормальные напряжения направлены в сторону внешней нормали соответствующей грани,
т.е. они вызывают деформацию растяжения элемента.
dy
2.
положительные касательные напряжения вращают элемент по часовой стрелке (при взгляде навстречу
оси z).
dx
A
В общем случае, напряжения в деформированном состоянии меняются от точки к точке, т.е. являются функциями
yx
координат. Здесь при рассмотрении бесконечно малого элемента можно считать, что напряженное состояние
σy
однородное и напряжения по каждой из граней постоянные и на параллельных гранях элемента равны между собой.
Выделенный элемент должен находиться в равновесии и удовлетворять уравнениям равновесия для произвольной плоской системы сил –
равнодействующих по каждой из граней приложенных напряжений:
Суммы проекций на координатные оси тождественно равны нулю.
yx xy
Составим сумму моментов относительно левого нижнего угла:
M Ai 0; - ( yx dxdz)dy ( xy dydz )dx 0.
σx
xy
x
Получен закон парности касательных напряжений: Касательные напряжения на двух взаимно перпендикулярных площадках
равны друг другу по величине и противоположны по знаку. В смежных гранях касательные напряжения направлены либо к общему ребру,
либо - от ребра.
yx<0
yx>0
Таким образом, показанные направления касательных напряжений на
рисунке, посвященном правилам знаков, не соответствуют
xy
xy<0
равновесному состоянию элемента. Возможные, правильные
направления касательных напряжений:
xy
xy>0
yx
yx
39

4. Лекция 8 (стр.40)

Главные напряжения - При расчете конструкций на прочность необходимо определить величину максимальных напряжений.
Максимальные и минимальные нормальные напряжения называются главными напряжениями, а площадки, по которым они действуют –
главными площадками.
Для определения положения главных площадок достаточно положить нулю первую производную нормальных напряжений по углу наклона:
x ( 2 cos ) sin y 2 sin cos yx 2 cos 2 ( x y ) sin 2 2 yx cos 2 0.
x cos 2 y sin 2 yx sin 2
tg 2
2 yx
x y
.
Поскольку тангенс имеет одинаковые значения для углов, отличающихся друг от друга на 1800, полученное выражение
определяет две площадки, отличающиеся друг от друга на 900. Таким образом, обе главные площадки взаимно
перпендикулярны.
Заметим, что производная нормальных напряжений в наклонной площадке по углу наклона
( x y ) sin 2 2 yx cos 2 2 .
оказывается равной удвоенной величине касательных напряжений по этой площадке:
Таким образом, на главных площадках касательные напряжения обращаются в нуль.
Для определения величины максимальных и минимальных нормальных напряжений надо найти значения угла через arctg(…) и подставить
в исходное выражение для нормальных напряжений, но проще непосредственно использовать следующие тригонометрические формулы:
2 yx
sin 2
tg 2
1 tg 2 2
x y
2 yx
1
y
x
2
2 yx
cos 2
( x y ) 2 4 yx2
cos 2
1
1 tg 2 2
x y
1 cos 2 1
2
2 2 ( x y ) 2 4 yx2
1
x y
2
( x y ) 2 4 yx2
2 yx
1
y
x
x y
1
cos 2 1
sin 2
2
2 2 ( x y ) 2 4 yx2
Подстановка этих тригонометрических функций в формулу нормальных напряжений дает для одной из главных площадок:
Поскольку угол для другой главной площадки
1
1
x y
x y
2 yx
0
x
y
yx
отличается от первой на 90 , то синус и косинус
2
2
2
2
2
2
двойного
угла
изменят
знак
на противоположный,
2 2 ( x y ) 4 yx
2 2 ( x y ) 4 yx
( x y ) 4 yx
что приведет к изменению знака второго слагаемого :
x y
2
( x y ) 2 4 2
yx
2 ( ) 2 4 2
x
y
yx
1
y
x
( x y ) 2 4 yx2 .
2
2
Таким образом, по двум главным площадкам
действуют главные напряжения:
max
x y
2
1
( x y ) 2 4 yx2 .
2
min
x y
2
x y
2
1
( x y ) 2 4 yx2 .
2
1
( x y ) 2 4 yx2 .
2
40

5. Лекция 8 (стр.41)

Максимальные касательные напряжения - Существуют площадки, в которых касательные напряжения достигают максимальных
значений. Для определения их положения достаточно положить нулю первую производную касательных напряжений по углу наклона:
x y
2
x y
2 cos 2 yx 2 sin 2 ( x y ) cos 2 2 yx sin 2 0.
2
sin 2 yx cos 2
tg 2 1
x y
.
2 yx
Поскольку тангенс имеет одинаковые значения для углов, отличающихся друг от друга на 1800, полученное выражение определяет две
площадки, отличающиеся друг от друга на 900. Таким образом, обе площадки взаимно перпендикулярны. Хотя в этих площадках в общем
случае нормальные напряжения на обращаются в ноль, площадки, в которых касательные напряжения максимальные,
2 yx
называют площадками сдвига.
Определим угол между площадкой сдвига и главной площадкой.
Сравним формулы для углов наклона главных площадок и площадок сдвига:
Поскольку правые части
обратные друг другу, то
tg 2 1
1
.
tg 2
900 2 1 2 .
ctg(90 0 2 1 ) ctg 2 .
tg 2
x y
.
1 450.
Таким образом, площадки сдвига повернуты относительно главных площадок на угол 450.
Для определения величины максимальных касательных напряжений надо найти значения угла через arctg(…) и подставить в исходное выражение
для касательных напряжений, но проще принять в качестве исходного состояния главные площадки и перейти к площадкам сдвига:
x y
2
sin 2 yx cos 2
max min
2
sin( 2 450 ) 0 cos( 2 450 )
max min
2
.
При подстановке угла 1350 или -450 (вторая площадка сдвига) получим тот же результат, но с обратным
знаком. Таким образом, вновь соблюдается закон парности касательных и в общем случае можно записать:
Подставим выражения
для главных напряжений:
max
x y
2
1
( x y ) 2 4 yx2 .
2
min
x y
2
max, min
max min
2
.
1
1
( x y ) 2 4 yx2 .
( x y ) 2 4 yx2 . max, min
2
2
Понятие о круге Мора для напряжений- Существуют графический способ определения положений главных площадок и напряжений, а
также напряжений по любым другим площадкам. Способ основан на том, что зависимость между нормальными и касательными
напряжениями описывается уравнением II порядка, а именно уравнением окружности:
x y x y
1 cos
1 cos
2
2
cos 2 yx sin 2
Итак,
получили
уравнение
II
порядка
cos
sin
sin
2
sin
2
x
y
yx
x
y
yx
2
2
2
2
2
2
2
2
x y
x y
2
Возведем
x y
yx2 . в квадрат x y 2 x y (cos 2 2 sin 2 2 ) 2 (sin 2 2 cos 2 2 )
yx
2
2 sin 2 yx cos 22 обе части уравнений
2
2
( x a) ( y b) R .
2
для напряжений
Сравните его с уравнением окружности:
и сложим:
2
2
2
x y
2
=0
=1
yx (sin 2 cos 2 sin 2 cos 2 ).
=1
41

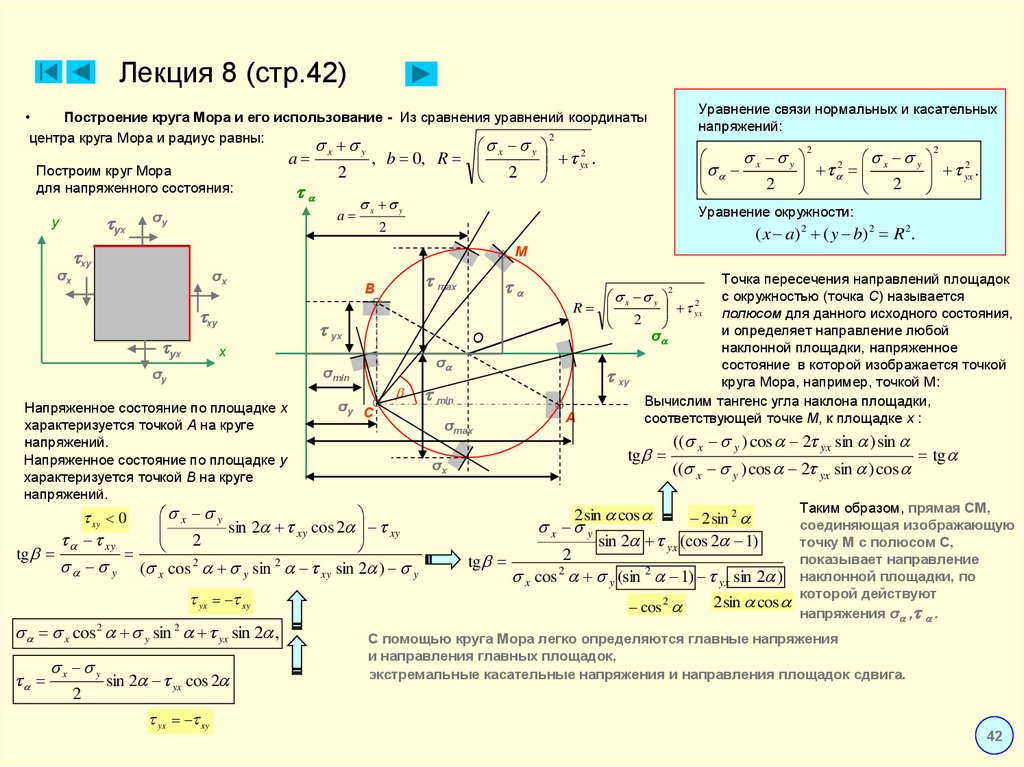
6. Лекция 8 (стр.42)

Уравнение связи нормальных и касательных
напряжений:
Построение круга Мора и его использование - Из сравнения уравнений координаты
2
центра круга Мора и радиус равны:
Построим круг Мора
для напряженного состояния:
yx
у
σx
a
x y
2
a
σy
xy
x y
yx2 .
, b 0, R
2
σx
yx
x y
( x a) 2 ( y b) 2 R 2 .
max
B
yx
σy С
x cos2 y sin 2 yx sin 2 ,
sin 2 yx cos 2
2
xy
min
σmax
Точка пересечения направлений площадок
с окружностью (точка C) называется
полюсом для данного исходного состояния,
и определяет направление любой
наклонной площадки, напряженное
состояние в которой изображается точкой
круга Мора, например, точкой M:
Вычислим тангенс угла наклона площадки,
соответствующей точке M, к площадке x :
x y
yx2
R
2
σ
σ
A
tg
σx
x y
xy 0
sin 2 xy cos 2 xy
xy
2
tg
2
2
y ( x cos y sin xy sin 2 ) y
yx xy
O
σmin
Напряженное состояние по площадке x
характеризуется точкой A на круге
напряжений.
Напряженное состояние по площадке y
характеризуется точкой B на круге
напряжений.
2
2
Уравнение окружности:
2
x
σy
x y
2
M
xy
y
y
x
2 x
yx2 .
2
2
2 sin cos
x y
tg
2
(( x y ) cos 2 yx sin ) sin
(( x y ) cos 2 yx sin ) cos
2 sin 2
sin 2 yx (cos 2 1)
x cos 2 y (sin 2 1) yx sin 2 )
2 sin cos
cos 2
tg
Таким образом, прямая CM,
соединяющая изображающую
точку M с полюсом C,
показывает направление
наклонной площадки, по
которой действуют
напряжения σ , .
С помощью круга Мора легко определяются главные напряжения
и направления главных площадок,
экстремальные касательные напряжения и направления площадок сдвига.
yx xy
42

7. Лекция 8 (стр.43)

Главные деформации - Подобно тому, как определялись напряжения на наклонных площадках, могут быть определены деформации.
Выражения деформаций в новой системе координат, повернутой относительно начальной на некоторый угол, аналогичны выражениям
для напряжений. Достаточно подставить вместо нормальных напряжений линейные деформации, а вместо касательных напряжений –
половины углов сдвига:
1
2
x cos 2 y sin 2 yx sin 2 ,
x
y
2
1
sin 2 yx cos 2 .
2
Так же, как и для напряжений, существуют такие площадки, для которых отсутствуют углы сдвига, а линейные деформации принимают
максимальные значения. Эти площадки и линейные деформации называются главными. Для их определения используются формулы,
аналогичные полученным для напряжений:
max
x
y
2
1
2
( x y ) 2 yx
.
2
tg 2
yx
x y
.
С помощью круга Мора, построенного для деформаций легко определяются главные деформации и направления главных
площадок.
43

8. Лекция 9(стр.44)

Геометрические характеристики поперечных сечений - Величина нормальных напряжений в поперечном сечении растянутого (сжатого)
стержня зависит от площади этого сечения. Таким образом, площадь поперечного сечения является геометрической
характеристикой, определяющей напряжение при растяжении (сжатии). В случае других видов напряженно-деформируемого
состояния (изгиб, кручение) напряжения зависят не от площади, а от некоторых других геометрических характеристик поперечного сечения.
Иерархия геометрических характеристик устанавливается видом подинтегрального выражения и представляется следующей:
Площадь поперечного сечения:
A dA
S x ydA;
A
yC
y
Статические
A
моменты площади поперечного сечения:
S y xdA.
A
dy
Статические моменты используются при определении положения центра тяжести:
dA
y
dx
x
Sy
A
; yC
Sx
.
A
xC Определение координат центра тяжести. Методы определения положения центра тяжести плоских фигур
рассматривались в курсе теоретической механики,
S yi xi Ai
S xi yi Ai .
например, метод разбиения:
xC
; yC
Ai
Ai
Ai
Ai
x
xC C
yC
O
xC
Здесь xi, yi – координаты центров тяжести простых фигур, для которых они известны или легко находятся.
Напомним процедуру определения положения центра тяжести:
1. выбрать произвольную (начальную) систему координат x, y;
2. разбить заданную фигуру на более простые фигуры.
3. вычислить статические моменты и использовать формулы координат центра тяжести.
Оси, проходящие через центр тяжести фигуры, называются центральными. Можно показать, что относительно центральных
осей статические моменты обращаются в ноль.
Пример 1 – Определить положение центра тяжести уголкового поперечного сечения.
1. Выбираем систему координат x, y с началом в нижнем левом углу сечения.
4
y
C
12
2
4
O
x1
x2
20
x1 2; y1 6;
20 4
A2 (20 4) 4 64; x 2
4 12; y 2 2;
2
S y1 x1 A1 2 48 96;
S x1 y1 A1 6 48 288;
2. Разбиваем фигуру на два прямоугольника,
вычисляем площади
и координаты центров тяжести каждого:
1
x
3. Вычисляем статические моменты
и координаты центра
тяжести всего сечения:
xC
A1 4 12 48;
S x 2 y 2 A2 2 64 128;
S y 2 x 2 A2 12 64 768;
S yi S y1 S y 2 96 768 864
S xi S x1 S x 2 288 128 416 3,71.
7,71. yC
A1 A2
48 64
112
A1 A2
48 64 112
Ai
Ai
44

9. Лекция 9 (стр.45)

y
dy
Моменты инерции площади поперечного сечения:
I x y dA;
2
I y x dA.
2
A
I xy xydA,
- осевые моменты инерции площади,
- центробежный момент
инерции площади.
A
A
y
I ( x y )dA dA. - полярный момент инерции площади.
2
2
2
A
A
O
dA
x
x
dx
Моменты инерции площади используются при определении напряжений при изгибе и кручении.
Можно показать, что центробежный момент инерции относительно осей, одна из которых совпадает с осью симметрии,
равен нулю. В самом деле, в этом случае элементарной площадке dA с координатами x, y всегда будет соответствовать такая же площадка
координатами –x, y или x, -y. Суммирование (интегрирование) произведений xydA даст нуль.
Далее будет показано, что для любой, в том числе несимметричной, фигуры можно найти такое положение осей, при котором центробежный
момент обращается в нуль. Полярный момент инерции не зависит ориентации координатных осей x, y
и всегда равен сумме осевых моментов инерции: I 2 dA. ( x 2 y 2 )dA x 2 dA y 2 dA I I .
y
x
A
A
A
A
Моменты инерции площади простейших сечений:
у yC
Прямоугольник
■ Треугольник
3 h
3
h
y
h
I x y 2 dA 0 y 2 bdy b 0 y 2 dy b
yC
A
xC C
yC
dy
h
xC
y
x
y
3
0
bh
.
3
Элементарная площадка имеет
переменную ширину и зависит от
ее координаты по оси y:
Известно, что центр тяжести прямоугольника находится
на пересечении осей симметрии (xC = b/2, yC = h/2).
Для вычисления моментов инерции относительно
центральных осей достаточно считать, что координата
y измеряется от центральной оси xC и изменить пределы
интегрирования:
b
h/2
h / 2
I xC
h/2
h / 2
y bdy b
2
3
Аналогично получим для других осей: I hb .
y
I yC
3
Центробежный момент инерции (по симметрии):
Полярный момент инерции:
I I xC I yC
y3
y dy b
3
h/2
2
h / 2
bh 3
.
12
2h / 3
hb
.
12
I xC
bh
b h bh(h b )
.
12
12
12
3
C
C
h y
h y
xC
; by
b;
yC
b
h
h
x
h y
dA b y dy
bdy.
b
h
h y
h
I x y 2 dA 0 y 2
bdy
h
h
A
b h 2
b y3 y 4
bh 3
3
0 (hy y )dy h
.
h
h 3
4
12
0
by
Момент инерции относительно центральной оси xC :
3
I xy 0.
3
x
dy h
y
2
2
b 2h / 3
b y3 y4
bh 3
h / 3 (hy 2 y 3 )dy h
.
h
h 3
4
36
h / 3
Момент инерции относительно центральной оси yC :
I yC 2 I yC (b / 2) 2
h(b / 2) 3 hb 3
.
12
48
45

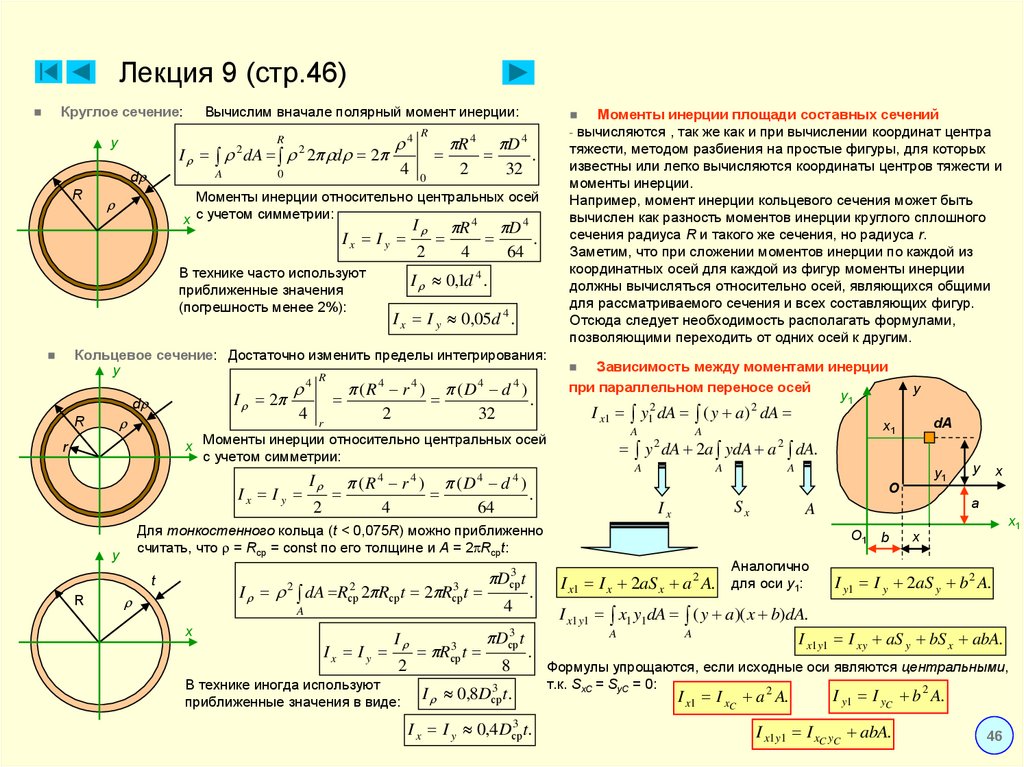
10. Лекция 9 (стр.46)

Круглое сечение:
R
y
I 2 dA 2 2 d 2
d
R
Вычислим вначале полярный момент инерции:
A
0
4 R
4
R 4
2
0
Моменты инерции площади составных сечений
вычисляются , так же как и при вычислении координат центра
тяжести, методом разбиения на простые фигуры, для которых
известны или легко вычисляются координаты центров тяжести и
моменты инерции.
Например, момент инерции кольцевого сечения может быть
вычислен как разность моментов инерции круглого сплошного
сечения радиуса R и такого же сечения, но радиуса r.
Заметим, что при сложении моментов инерции по каждой из
координатных осей для каждой из фигур моменты инерции
должны вычисляться относительно осей, являющихся общими
для рассматриваемого сечения и всех составляющих фигур.
Отсюда следует необходимость располагать формулами,
позволяющими переходить от одних осей к другим.
-
D 4
.
32
Моменты инерции относительно центральных осей
x с учетом симметрии:
4
4
I
Ix Iy
В технике часто используют
приближенные значения
(погрешность менее 2%):
2
R
4
D
.
64
I 0,1d 4 .
I x I y 0,05d 4 .
Кольцевое сечение: Достаточно изменить пределы интегрирования:
y
R
R
I 2
d
4
Ix Iy
r
(R r )
4
2
(D d )
4
4
32
.
I
2
(R 4 r 4 )
4
(D 4 d 4 )
64
.
Для тонкостенного кольца (t < 0,075R) можно приближенно
считать, что = Rср = const по его толщине и A = 2 Rсрt:
t
R
R
4
x Моменты инерции относительно центральных осей
с учетом симметрии:
r
y
4
I dA
2
2
Rср
2 Rсрt
3
2 Rср
t
A
x
Ix Iy
I
2
В технике иногда используют
приближенные значения в виде:
3
Rср
t
3
Dср
t
4
3
Dср
t
8
.
.
3
I 0,8Dср
t.
3
I x I y 0,4Dср
t.
Зависимость между моментами инерции
при параллельном переносе осей
y1
I x1
y12 dA
A
( y a) dA
y
2
dA
x1
A
y dA 2a ydA a dA.
2
A
2
A
A
y1
O
Ix
Sx
O1 b
Аналогично
x
a
A
I x1 I x 2aS x a 2 A. для оси y1:
y
x1
x
I y1 I y 2aS y b 2 A.
I x1 y1 x1 y1dA ( y a)( x b)dA.
A
A
I x1 y1 I xy aS y bS x abA.
Формулы упрощаются, если исходные оси являются центральными,
т.к. SxC = SyC = 0:
2
2
I x1 I xC a A.
I y1 I yC b A.
I x1y1 I xC yC abA.
46

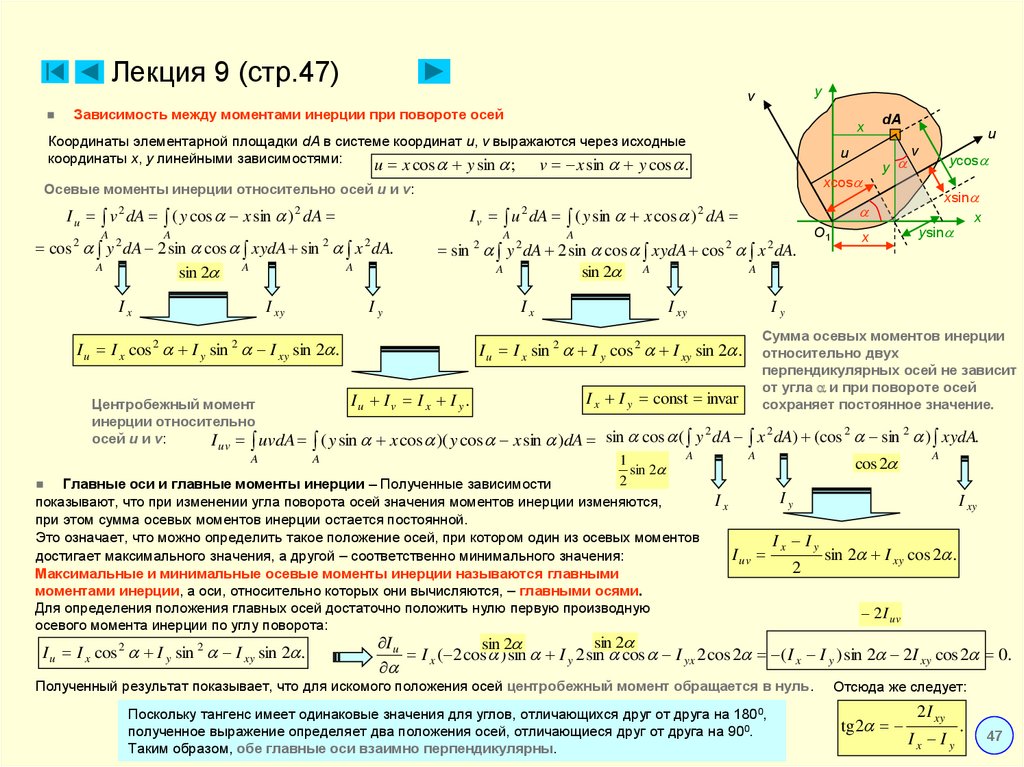
11. Лекция 9 (стр.47)

y
v
Зависимость между моментами инерции при повороте осей
x
Координаты элементарной площадки dA в системе координат u, v выражаются через исходные
координаты x, y линейными зависимостями:
u x cos y sin ;
u
v x sin y cos .
xcos
Осевые моменты инерции относительно осей u и v:
2
2
A
A
cos 2 y 2 dA 2 sin cos xydA sin 2 x 2 dA.
A
A
sin 2 A
Ix
I xy
Iy
I u I x cos 2 I y sin 2 I xy sin 2 .
Центробежный момент
инерции относительно
осей u и v:
I uv uvdA
A
A
2
A
sin y dA 2 sin cos xydA cos x dA.
A
A
sin 2 A
2
2
Ix
2
I xy
y
O1
x
v
ycos
xsin
x
ysin
Iy
I x I y const invar
Сумма осевых моментов инерции
относительно двух
перпендикулярных осей не зависит
от угла и при повороте осей
сохраняет постоянное значение.
2
2
2
2
( y sin x cos )( y cos x sin )dA sin cos ( A y dA A x dA) (cos sin ) A xydA.
cos 2
A
1
sin 2
2
Главные оси и главные моменты инерции – Полученные зависимости
показывают, что при изменении угла поворота осей значения моментов инерции изменяются,
при этом сумма осевых моментов инерции остается постоянной.
Это означает, что можно определить такое положение осей, при котором один из осевых моментов
достигает максимального значения, а другой – соответственно минимального значения:
Максимальные и минимальные осевые моменты инерции называются главными
моментами инерции, а оси, относительно которых они вычисляются, – главными осями.
Для определения положения главных осей достаточно положить нулю первую производную
осевого момента инерции по углу поворота:
I u I x cos 2 I y sin 2 I xy sin 2 .
2
I u I x sin 2 I y cos 2 I xy sin 2 .
Iu Iv I x I y .
u
I v u dA ( y sin x cos ) dA
I u v dA ( y cos x sin ) dA
2
dA
Iy
Ix
I uv
Ix Iy
2
I xy
sin 2 I xy cos 2 .
2 I uv
sin 2
I u
sin 2
I x ( 2 cos ) sin I y 2 sin cos I yx 2 cos 2 ( I x I y ) sin 2 2I xy cos 2 0.
Полученный результат показывает, что для искомого положения осей центробежный момент обращается в нуль.
Поскольку тангенс имеет одинаковые значения для углов, отличающихся друг от друга на 1800,
полученное выражение определяет два положения осей, отличающиеся друг от друга на 900.
Таким образом, обе главные оси взаимно перпендикулярны.
Отсюда же следует:
tg 2
2 I xy
Ix Iy
.
47

12. Лекция 9 (стр.48)

Для определения величины максимальных и минимальных моментов инерции (главных моментов инерции) надо найти значения угла через
arctg(…) и подставить в исходное выражение для осевых моментов инерции, или непосредственно использовать тригонометрические формулы
двойных углов, как это было сделано, например, при определении главных напряжений (лекция 10). Здесь попробуем чуть иначе.
Представим осевой момент в виде:
I u I x cos 2 I y sin 2 I xy sin 2 .
Iu
1 cos 2
cos 2
2
1 cos 2
2
sin
2
Ix Iy
2
Ix Iy
2
Iu
cos 2 I xy sin 2
tg 2
2 I xy
Ix Iy
I x I y sin 2
2
cos
2
Подставляя последнее выражение и сокращая
Ix Iy 1
2
2
I x I y 4 I xy
.
разность моментов инерции получаем окончательно: I u
2
2
Ix Iy
2
Ix Iy
2
1
.
cos 2
.
tg 2
Знак плюс перед вторым слагаемым относится к максимальному моменту, знак минус – к минимальному.
2 I xy
Ix Iy
1 tg 2 2
.
1
Ix Iy
2
( I x I y ) 2 4 I xy
48

13. Лекция 9 (стр.49)

Радиус инерции – есть величина, связывающая момент инерции с площадью поперечного сечения и определяемая из равенств:
Радиус инерции представляет собой расстояние от рассматриваемой оси до той точки, в которой условно можно сосредоточить
всю площадь поперечного сечения. Эта величина характеризует насколько хорошо “развито” сечение, как далеко отстоят от оси
отдельные области сечения, что в свою очередь характеризует экономичность сечения при изгибе и сжатии с изгибом.
Радиусом инерции удобно пользоваться при оценке гибкости сжатых стержней.
Конечно для этого радиусы инерции предварительно вычисляются для типовых и прокатных сечений по формулам:
Радиусы инерции, соответствующие главным осям, называются
главными радиусами инерции и определяются по формулам:
imax
I max
.
A
imin
I min
.
A
ix
Ix
.
A
I x i x2 A.
I y i y2 A.
iy
Iy
A
Вычисление моментов инерции сложных фигур – выполняется в следующем порядке:
Сечение разбивается на части, для которых известны координаты центров тяжести и моменты инерции или легко находятся.
Выбираются начальные оси, относительно которых вычисляются координаты центра тяжести сечения.
Вычисляются координаты центра тяжести сечения.
Проводятся центральные оси (проходящие через центр тяжести сечения), относительно которых вычисляются моменты инерции.
Вычисляются осевые и центробежные моменты инерции сечения относительно центральных осей.
Вычисляются главные центральные моменты и определяется положение главных осей.
1.
2.
3.
4.
5.
6.
Пример 1 – Определить главные
центральные моменты
и положение главных осей
уголкового поперечного сечения.
y
t
2
yC
1
C
h
1
2
xC
t
O
x1
x
x2
a
49
.

14. Лекция 10 (стр.50)

Понятие о чистом сдвиге – Кроме деформации растяжения или сжатия материал нагруженного элемента конструкции может
испытывать деформацию сдвига. Примером этому может служить напряженно-деформированное состояние элемента стенки балки в
произвольном сечении, рассмотренное в предыдущей лекции. Там же было показано, что в опорных сечениях на нейтральной оси на
гранях элемента отсутствуют нормальные напряжения, а касательные напряжения максимальны.
Другим примером, можно сказать классическим, является кручение тонкостенной трубы,
z
zy
z
при котором любой элемент находится только под действием касательных напряжений.
y
Напряженно-деформированное состояние, характеризуемое тем, что на гранях
yz
элемента возникают только касательные напряжения, называют чистым сдвигом.
Закон Гука сдвиге – Деформации чистого сдвига экспериментально изучаются
путем кручения трубчатых образцов. Экспериментальная диаграмма сдвига,
связывающая напряжения и угол сдвига, для пластичной стали имеет такой же характер
изменения, как и диаграмма растяжения:
До напряжения пц , называемого пределом пропорциональности
при сдвиге справедлива линейная зависимость
(закон Гука при сдвиге):
G .
dz
tg = G
y
1
dy
A
yz
zy
y
x
tg
y
.
dy
ds (ds cos 45 0 ) cos 45 0 ds cos 2 45 0.
ds 1
1
(1 )
( 1 2 ) ( ( ))
.
ds
E
E
E
ds
ds y cos 45 0.
ds
Удлинение диагонали элемента вследствие деформации растяжения (σ1 = , σ2 = - ):
ds
dz
A
Удлинение диагонали элемента вследствие деформации сдвига (dy = dz):
ds dy cos 45 0.
ds
dy
Касательное напряжение, при котором угол сдвига
возрастает при постоянном напряжении называется
пределом текучести при сдвиге.
■ Связь между модулем сдвига и модулем упругости при растяжении – Модуль сдвига и модуль
упругости при растяжении являются физическими постоянными материала, характеризующими
жесткость в каждом из этих двух видов деформации. Поскольку удлинение диагонали элемента,
вызванное сдвигом, может быть получено также растяжением этого волокна под действием
нормальных напряжений, эти константы должны быть связаны между собой некоторым соотношением:
Здесь - относительный сдвиг:
G – модуль сдвига.
Т
пц
y
G
(1 )
ds.
E
Таким образом существует соотношение между модулем сдвига и модулем упругости при
растяжении с участием коэффициента Пуассона. Любую из этих величин можно определить,
если известны две другие.
ds cos 2 45 0
2G
ds.
(1 )
1
.
E
2G
или
G
E
.
2(1 )
50

15. Лекция 10 (стр.51)

Кручение стержней круглого поперечного сечения – Кручение характерно тем, что в поперечных сечениях возникают касательные
напряжения , приводящиеся к крутящему моменту Mz.
Деформация стержня при кручении выражается тем, что поперечные сечения поворачиваются вокруг оси стержня
z на некоторые углы = (z) , называемые углами закручивания.
y
x
Касательные напряжения при кручении – Как указывалось ранее, задача
определения напряжений является статически неопределимой, для решения которой
необходимо последовательно рассмотреть три стороны задачи:
z
1. Статика: Выделим малый элемент двумя нормальными к оси бруса сечениями
и заменим действие отброшенных частей касательными напряжениями.
Под их действием элемент находится в равновесии.
Ранее приведением распределенных сил к центру и центральным осям было
получено интегральное соотношение, связывающие крутящий момент
с касательными напряжениями: M ( x y)dA
Mz
dz
z
y
Mz
z
zy
x
K1
dφ z
K
y
zy
zx
A
zx
Касательное напряжение произвольного направления в каждой точке
плоскости поперечного сечения можно разложить по двум другим
направлениям, а именно, по радиусу , соединяющему точку с центром
x тяжести сечения, и по перпендикуляру к этому радиусу. Момент
относительно центральной оси z будет создавать лишь вторая компонента,
обозначаемая одним символом . Тогда:
M dA
z
A
dz
Mz
Из этого соотношения найти напряжение по известному крутящему моменту пока
нельзя, поскольку закон изменения напряжений по радиусу сечения неизвестен.
2. Геометрия: Согласно гипотезе плоских сечений при своем повороте сечения остаются плоскими (справедливо лишь для круглых сечений).
Следующее допущение состоит в том, что все радиусы сечения остаются прямыми и поворачиваются на один тот же угол (угол закручивания).
3. Физика: По закону Гука при сдвиге:
Подставляем в интеграл:
M z G
A
G .
d 2
d
d
dA G
2 dA G
I p.
dz
dz A
dz
Подставляем в выражение
для напряжений:
Mz
.
Ip
G
d
d
.
dz
Mz
dz
GI p
51

16. Лекция 10 (стр.52)

Анализ напряженного состояния при кручении – По закону парности касательных напряжений полученная формула для касательных
напряжений, возникающих в поперечном сечении, одновременно определяет касательные напряжения в плоскости, перпендикулярной
продольному диаметральному сечению:
Каждый прямоугольный элемент материала испытывает напряженное состояние чистого сдвига.
Определение углов закручивания – При выводе формулы касательных напряжений
при кручении была получена дифференциальная зависимость:
Mz
dz
GI p
d
Mz
z
Угол закручивания определяется из этого
дифференциального соотношения интегрированием
левой и правой части:
z
Mz
где 0 – угол поворота при z = 0.
GI p
z0
Mz
dz 0 ,
В частном случае при постоянном моменте Mz, постоянной жесткости GIpи неподвижном
сечении в начале координат (φ0 = 0) получаем:
l
Этой формулой можно пользоваться при определении угла для вала постоянного или
ступенчато постоянного сечения, нагруженного сосредоточенными моментами.
При этом на каждом из участков, на котором крутящий момент, жесткость постоянны, угол закручивания
изменяется по линейному закону. Как следует из общей формулы определения угла закручивания, при
построении эпюры углов закручивания ординаты эпюры откладываются от уровня предыдущего угла
закручивания, т.е. строятся нарастающим итогом, учитывая угол закручивания предыдущего участка.
M z
M l
z z .
GI p
GI p
0
1
z1
I
Пример: Построить эпюру углов закручивания для стержня нагруженного сосредоточенными моментами:
M1=5M, M2=4M, где M – параметр нагрузки, Ip2/Ip1 = 2.
M zI I z1
Ml
1. Сечение I-I (0 < z1< l):
.
M1 M 2 5M 4M M . 1
GI p1
GI p1
z1 l
II II
M ziсправа M 2 4M .
2. Сечение II-II (0 < z2< l): M z
II II
M
z2
Ml
( 4M )l
Ml
2 1 z
.
GI p 2
GI p1
2GI p1
GI p1 M
M zI I
M ziсправа
z1 l
Расчеты на жесткость – Валы машин испытывают переменные (динамические) нагрузки. При малой
жесткости валов могут возникать нежелательные крутильные колебания. Поэтому, помимо условий прочности
должны выполняться условия жесткости, ограничивающие величину максимального угла закручивания,
отнесенного к длине (погонного угла закручивания):
max
Mz
расч.
GI p
2
z2 II
M2
z
I
II
l
l
M1
M
+
Mz
Ml
4M
GI p1
+
Ml
GI p1
4M
φ
52