Похожие презентации:
Геометрические характеристики плоских сечений
1. Геометрические характеристики плоских сечений
Различают следующие характеристики сечений: площадь А, статическиймомент площади (SX, или SY ), момент инерции площади (IX, или IY),
центробежный момент инерции площади (IXY).
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
SX
YdA
SY
A
A
Y
X
Оси, проходящие через центр тяжести,
называются центральными осями.
dА
XdA
Моменты площади фигуры относительно
центральных осей равны нулю
А
Y
Координаты центра тяжести
XC
X
SY
;
A
YC
SX
A
2.
Геометрические характеристики плоских сеченийМоментом инерции площади относительно оси называется сумма
произведений площадей элементарных площадок на квадрат расстояний
от их центра тяжести до соответствующей оси.
I X Y 2 dA
I Y X 2 dA
A
A
Центробежным моментом инерции называется сумма произведений
площадей элементарных площадок на расстояния от центра тяжести до осей
I XY
XYdA
A
Полярным моментом инерции называется сумма произведения площадей
элементарных площадок на квадрат расстояния от центра тяжести до начала
координат
I 2 dA
A
A
X Y
2
2
I 2dA X 2 Y 2 dA X 2dA Y 2dA IY I X
2
A
A
A
Полярный момент инерции равен сумме осевых моментов
инерции относительно взаимно перпендикулярных осей.
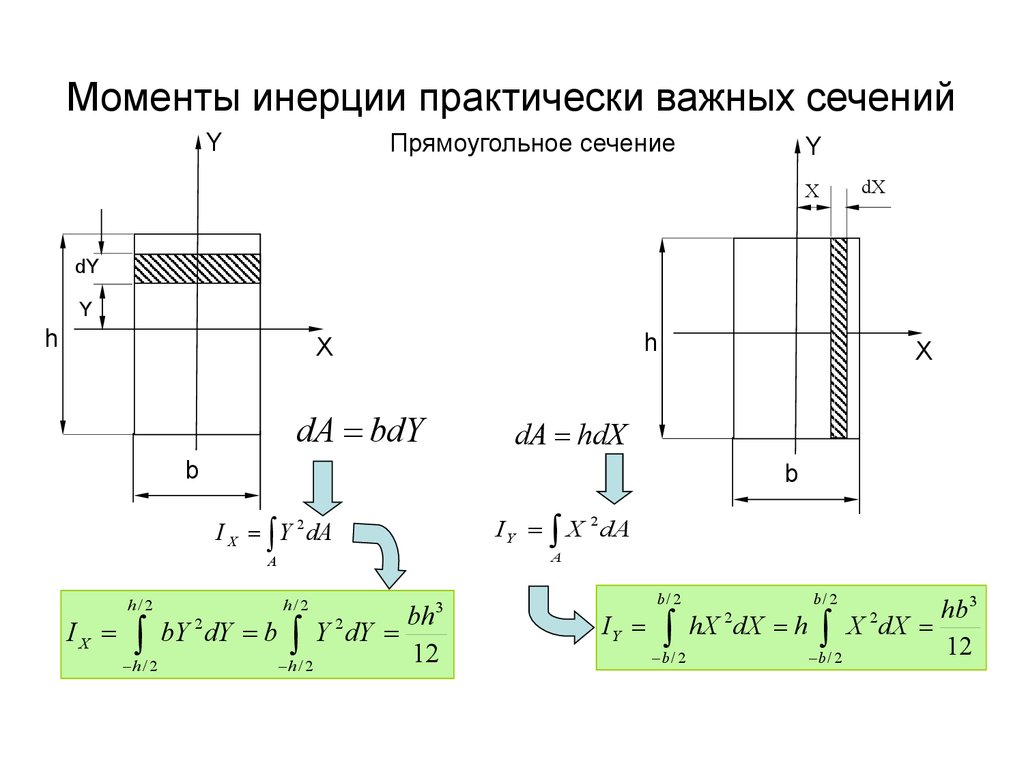
3. Моменты инерции практически важных сечений
YПрямоугольное сечение
Y
X
dX
dY
Y
h
h
X
dA bdY
X
dA hdX
b
b
I X Y 2 dA
A
h/2
h/2
bh 3
2
2
I X bY dY b Y dY
12
h / 2
h / 2
IY
X
2
dA
A
b/2
b/2
hb 3
I Y hX dX h X dX
12
b / 2
b / 2
2
2
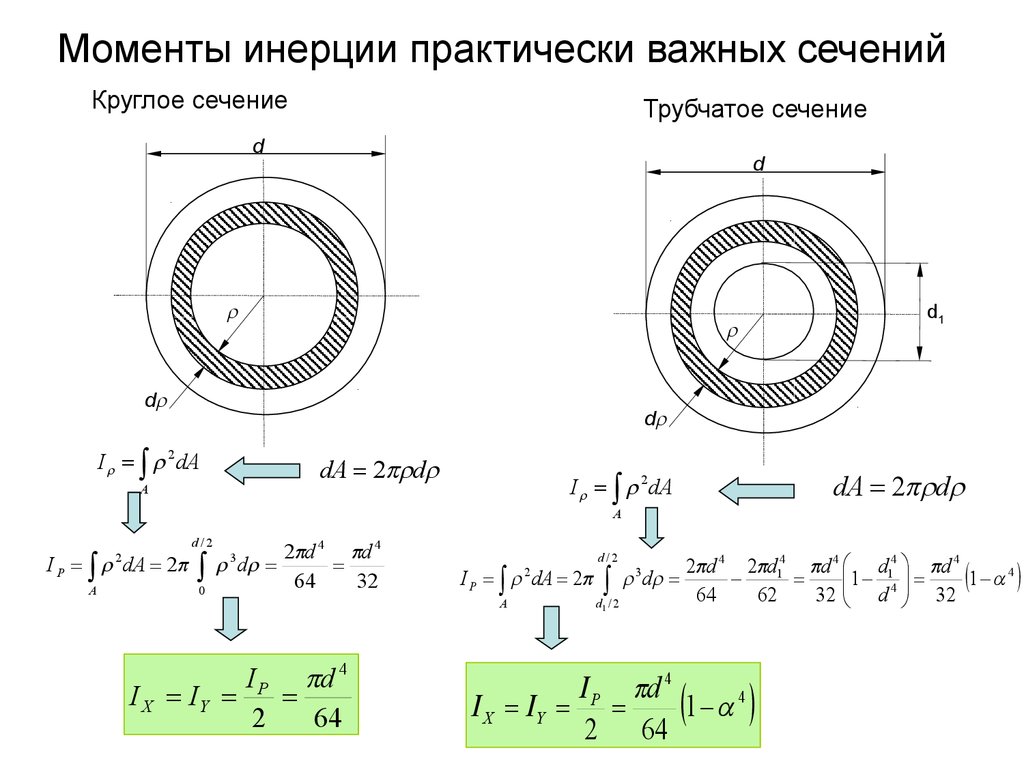
4. Моменты инерции практически важных сечений
Круглое сечениеТрубчатое сечение
d
d
d
d1
d
I 2 dA
dA 2 d
A
I 2 dA
dA 2 d
A
I P dA 2
2
A
d /2
0
2 d 4 d 4
d
64
32
3
I P d 4
I X IY
2
64
2 d 4 2 d14 d 4 d14 d 4
1 4
I P dA 2 d
1 4
64
62
32 d 32
A
d1 / 2
d /2
2
3
I P d 4
I X IY
1 4
2 64
5. Изменение моментов инерции при параллельном переносе осей
Координаты текущей точки в новой системе координат равны: XC+X и YC+YYС
Y
XС
Осевые моменты инерции
X
I X YC Y dA Y 2 dA 2YC YdA YC2 dA
2
A
A
A
A
dА
I X Y 2dA; S X YdA 0;
Y
А
A
XС
YС
A dA
A
I X I Xc YC2 A
A
I Y I Yc X C2 A
Центробежные моменты инерции
I XY X X C Y YC dA
X
I XY X X C Y YC dA I XcYc X CYC A
A
XYdA YC XdA X C YdA X CYC dA
A
A
A
A
A
I XcYc XYdA; SY XdA 0; S X YdA 0; A dA
A
A
A
A
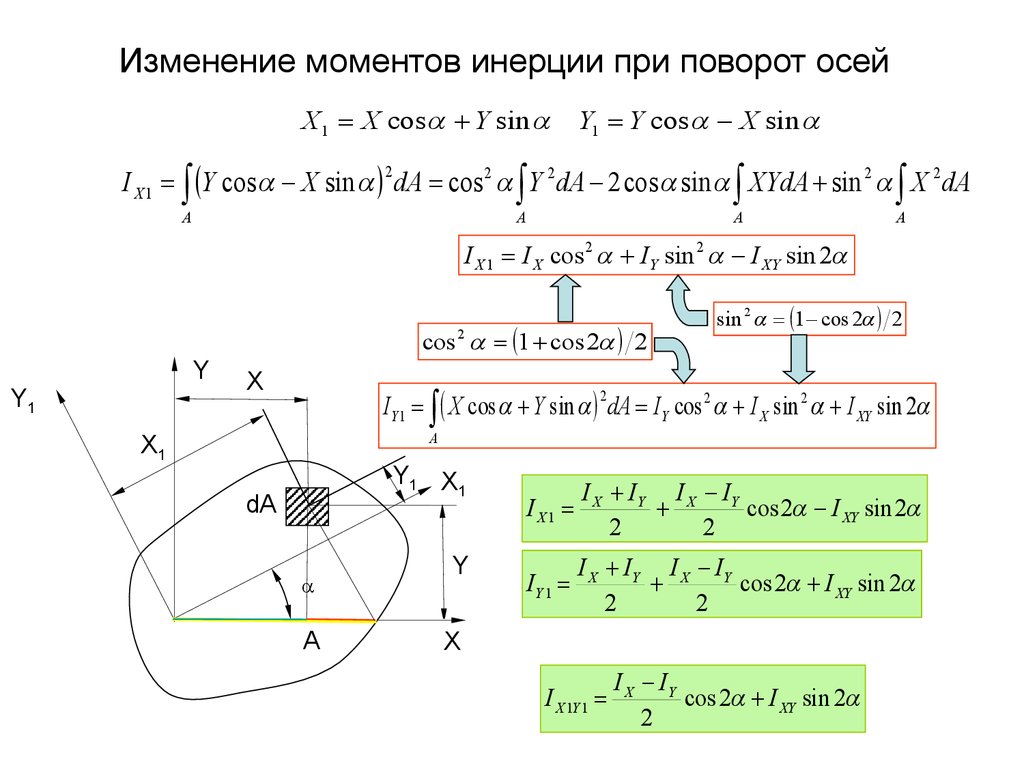
6. Изменение моментов инерции при поворот осей
X 1 X cos Y sinY1 Y cos X sin
I X 1 Y cos X sin dA cos 2 Y 2 dA 2 cos sin XYdA sin 2 X 2 dA
2
A
A
A
A
I X 1 I X cos 2 IY sin 2 I XY sin 2
Y
Y1
cos 2 1 cos 2 2
X
sin 2 1 cos 2 2
IY 1 X cos Y sin dA IY cos 2 I X sin 2 I XY sin 2
2
A
X1
Y1 X1
dА
А
Y
I X1
I X IY I X IY
cos 2 I XY sin 2
2
2
IY 1
I X IY I X IY
cos 2 I XY sin 2
2
2
X
I X 1Y 1
I X IY
cos 2 I XY sin 2
2
7. Главные оси и главные моменты инерции
Главными осями называются оси, относительно которых центробежныймомент инерции равен нулю.
I X 1Y 1
I X IY
cos 2 I XY sin 2
2
I X 1Y 1
I X IY
cos 2 I XY sin 2 0
2
tg 2 0
2 I XY
I X IY
В результате решения трансцендентного уравнения получаем два
значения угла с разницей в /2 следовательно, главных осей две, и они
взаимно перпендикулярны.
I I
I I
I X 1 X Y X Y cos 2 I XY sin 2
2
2
dI X
2 I X cos sin 2 IY sin cos 2 I XY cos 2 0
d
Таким образом, главными осями можно считать оси, относительно которых
осевые моменты инерции достигают своих экстремальных (максимального и
минимального) значений.
Моменты инерции относительно главных осей называются главными
моментами инерции.
I мак , мин
I X IY 1
2
2
I X IY 2 4 I XY2




 Математика
Математика Физика
Физика








