Похожие презентации:
Решение логических задач. Лекция №13
1.
Лекция №132.
Решение логических задач табличнымспособом
При использовании этого способа
условия, которые содержит задача, и
результаты рассуждений фиксируются с
помощью
специально
составленных
таблиц.
3.
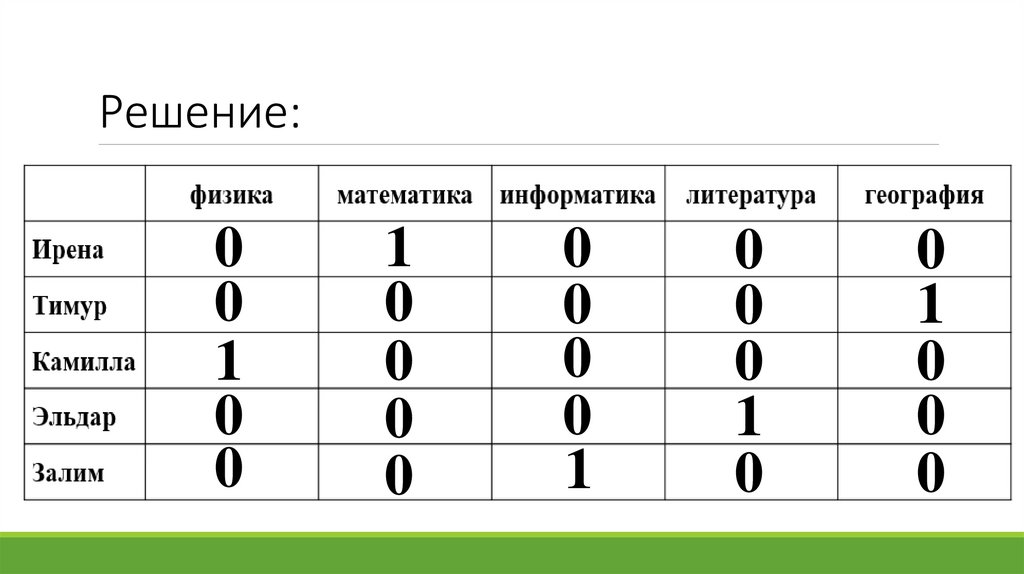
Задача 1.Пятеро одноклассников: Ирена, Тимур, Камилла, Эльдар и Залим стали
победителями олимпиад школьников по физике, математике, информатике,
литературе и географии. Известно, что:
1. Победитель олимпиады по информатике учит Ирену и Тимура работе на
компьютере;
2. Камилла и Эльдар тоже заинтересовались информатикой;
3. Тимур всегда побаивался физики;
4. Камилла, Тимур и победитель олимпиады по литературе занимаются плаванием;
5. Тимур и Камилла поздравили победителя олимпиады по математике;
6. Ирена сожалеет о том, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
4.
Решение:0
0
1
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
0
5.
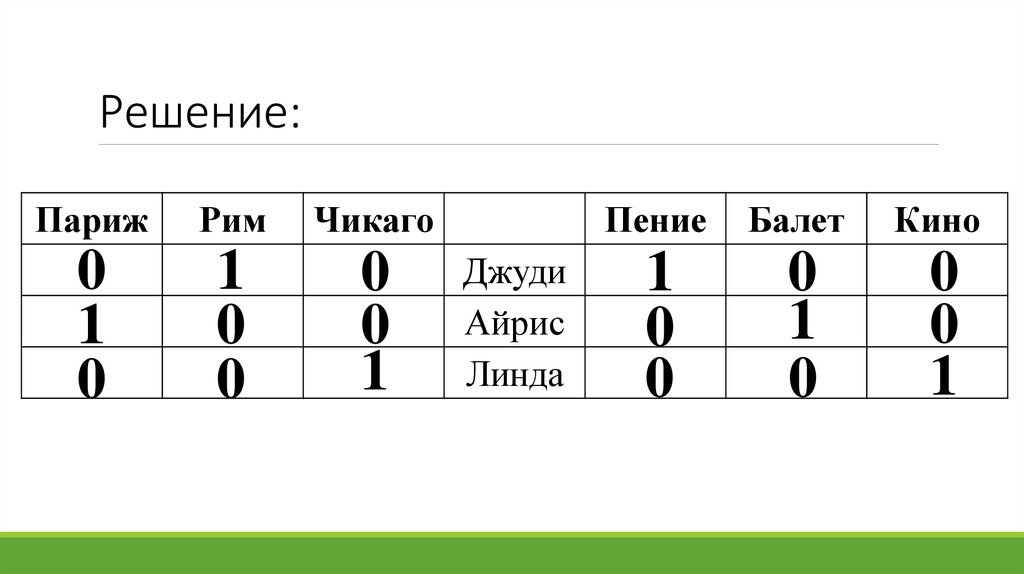
Задача 2.Три дочери писательницы Дорис Кей - Джуди, Айрис и Линда - тоже очень
талантливы. Они приобрели известность в разных видах искусств - пении, балете и
кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж,
Рим и Чикаго.
Известно, что:
1) Джуди живёт не в Париже, а Линда - не в Риме;
2)парижанка не снимается в кино;
3) та, кто живёт в Риме, певица;
4) Линда равнодушна к балету.
Где живёт Айрис и какова её профессия?
6.
Решение:Париж
Рим
Чикаго
0
1
0
1
0
0
0
0
1
Джуди
Айрис
Линда
Пение
Балет
Кино
1
0
0
0
1
0
0
0
1
7.
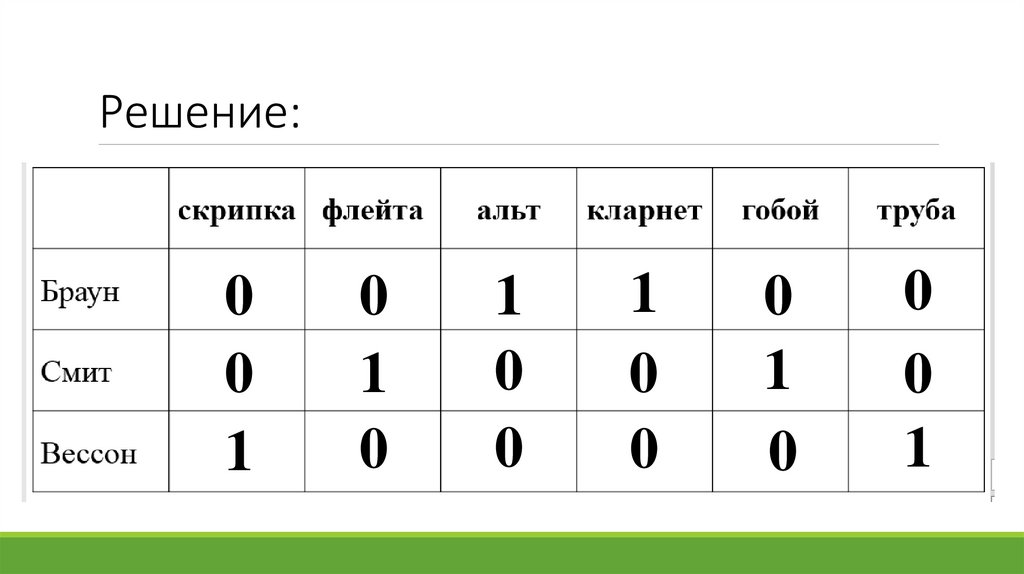
Задача 3.В симфонический оркестр приняли на работу трех музыкантов: Брауна, Смита
и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1) Смит самый высокий;
2) играющий на скрипке меньше ростом, чем играющий на флейте;
3) играющие на скрипке и флейте и Браун любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Смит мирит их;
5) Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет
двумя инструментами?
8.
Решение:0
0
1
0
1
0
1
0
0
1
0
0
0
1
0
0
0
1
9.
Решение логических задач с помощьюлогических операций
Для решения многих логических задач необходимо:
1. выделить в условии задачи простые высказывания и обозначить их буквами;
2. соединив простые высказывания в сложные с помощью логических операций.
Записать единую логическую функцию, отражающую условие задачи;
3. минимизировать полученное выражение;
4. выбрать решение – набор значений простых высказываний, при которых
построенное логическое выражение является истинным;
5. проверить, удовлетворяет ли полученное решение условию задачи.
При решении логических задач приходится оперировать громоздкими выражениями,
поэтому для обозначения логического сложения удобнее использовать знак +, а для
умножения знак * или вообще его опускать.
10.
Задача 4.При составлении расписания уроков в школе учитель
математики просил, чтобы его урок был первым или
вторым; историк мог давать либо первым, либо третий
уроки, а преподаватель литературы – только второй или
третий. Как следует составить расписание, чтобы
удовлетворить требования всех учителей? Сколько
вариантов может быть?
11.
Решение:1. выделить в условии задачи простые высказывания и обозначить их буквами;
Обозначим простые высказывания:
«Математика будет 1-м уроком» - М1,
«Математика будет 2-м уроком» - М2,
«История будет 1-м уроком» - I1,
«История будет 3-м уроком» - I3,
«Литература будет 2-м уроком» - L2,
«Литература будет 3-м уроком» - L3.
12.
Решение:2. соединив простые высказывания в сложные с помощью логических
операций. Записать единую логическую функцию, отражающую условие
задачи;
Запишем требования учителей:
(M1+M2)*(I1+I3)*(L2+L3)=1
13.
Решение:3. минимизировать полученное выражение;
Упростим полученное произведение:
(M1+M2)*(I1+I3)*(L2+L3)=
=(M1*I1+M1*I3+M2*I1+M2*I3)*(L2+L3)=
=M1*I3*L2+ M1*I3*L3 +M2*I1*L2+
+M2*I1*L3+M2*I3*L2+M2*I3*L3=
=M1*I3*L2+M2*I1*L3=1
14.
Решение:4. выбрать решение – набор значений простых высказываний, при которых
построенное логическое выражение является истинным;
M1*I3*L2+M2*I3*L3=1
Дизъюнкция высказываний истинна, когда хотя бы одно
из высказываний истинно. Следовательно, M1*I3*L2=1,
либо M2*I3*L3=1 (одновременно истинными эти
высказывания не могут быть по условию).
15.
Решение:5. проверить, удовлетворяет ли полученное решение условию задачи.
Конъюнкция высказываний истинна тогда и только тогда,
когда каждое из высказываний истинно. Значит, M1=1, I3=1,
L2=1, либо M2=1, I3=1, L3=1.
Ответ: Таким образом, возможны 2 варианта расписания, они
не противоречат условию задачи:
1 урок – математика, 2 урок – литература, 3 урок – история.
1 урок – история, 2 урок – математика, 3 урок – литература.
16.
Задача 5.Идет чемпионат школы по гимнастике. Болельщики горячо
обсуждают
ход борьбы и высказывают немало предложений
о будущих
победителях.
- Первой будет Наталья, а Майя будет второй, - сказал Серёжа.
- Нет, Лида займет второе место, а Рита будет четвертой, - возразил
Вова.
- Второй будет Наташа, а Рита – третьей, - авторитетно заявил Толя.
Когда соревнования закончились, оказалось , что каждый из
мальчиков ошибся, только один раз. Какие места заняли Наталья,
Майя, Рита и Лида?
17.
Решение:1. выделить в условии задачи простые высказывания и обозначить их буквами;
Обозначим простые высказывания:
«Наталья будет 1-й» - N1,
«Майя будет 2-й» - M2,
«Лида будет 2-й» - L2,
«Рита будет 4-й» - R4,
«Рита будет 3-й» - R3,
«Наталья будет 2-й» - N2.
18.
Решение:2. соединив простые высказывания в сложные с помощью логических операций.
Записать единую логическую функцию, отражающую условие задачи;
Болельщики были прав только в одном из своих предположений и только в одном.
Таким образом, либо имеет место N1=1 и одновременно с этим M2=0. Тогда N1* M 2 1 .
Либо имеет место M2=1 и одновременно с этим N1=0. В этом случае M 2 * N1 1. Значит,
N1* M 2 N1* M 2 1 .
Рассуждая таким же образом, составляем формулы высказываний второго и третьего
болельщика: L2 * R 4 L2 * R 4 1 и N 2 * R3 N 2 * R3 1 .
19.
Решение:Конъюнкция истинных высказываний является истинной:
.
N1* M 2 N1* M 2 * L2 * R4 L2 * R4 * N 2 * R3 N 2 * R3 1
20.
Решение:3. минимизировать полученное выражение;
Упростим полученное выражение, исключая ложные высказывания:
N1* M 2 N1* M 2 * L2 * R4 L2 * R4 * N 2 * R3 N 2 * R3
N1* M 2 * L 2 * R 4 N1* M 2 * L 2 * R 4 N1* M 2 * L 2 * R 4 N1* M 2 * L 2 * R 4 *
* N 2 * R3 N 2 * R3 N1* M 2 * L 2 * R 4 N1* M 2 * L 2 * R 4 * N 2 * R3 N 2 * R3
N 1* M 2 * L 2 * R 4 * N 2 * R3 N 1* M 2 * L 2 * R 4 * N 2 * R3 N 1* M 2 * L 2 * R 4 * N 2 * R3
N 1* M 2 * L 2 * R 4 * N 2 * R3 N 1* M 2 * L 2 * R 4 * N 2 * R3 1
21.
Решение:4. выбрать решение – набор значений простых высказываний, при которых
построенное логическое выражение является истинным;
N1* M 2 * L2 * R4 * N 2 * R3 1
22.
Решение:5. проверить, удовлетворяет ли полученное решение условию задачи.
Из истинности конъюнкции следует: N1=1, L2=1, R3=1, т.е. 1
место заняла Наташа, 2 место – Лида, 3 место – Рита, 4 место
остается Майе. То не противоречит условию.
Ответ:
1 место – Наташа,
2 место – Лида,
3 место – Рита,
4 место – Майя
23.
Задача 6.По подозрению в совершённом убийстве задержали Брауна, Джона и Смита.
Один из них был уважаемым в городе стариком, второй был малоизвестным
чиновником, а третий – известным мошенником. В процессе следствия
старик говорил правду, мошенник лгал, а третий задержанный говорил в
одном случае ложь, в другом правду. Вот что они утверждали:
Браун: «Я не делал этого. Джон не виноват.»
Джон: « Браун не виноват. Преступление совершил Смит»
Смит: « Я не виноват, виноват Браун»
Определите имя старика, мошенника и чиновника и кто из них виновен,
если известно, что преступник один.
24.
Решение:1. выделить в условии задачи простые высказывания и обозначить их буквами;
Обозначим простые высказывания:
B-виноват Браун
D-виноват Джон
C-виноват Смит.
Утверждения подозреваемых можно выразить формулами:
Браун: B * D
Джон: B * C
Смит: C * B
25.
Решение:2. соединив простые высказывания в сложные с помощью логических операций.
Записать единую логическую функцию, отражающую условие задачи;
По условию одно из тих сложных высказываний истинно, так как один
подозреваемый – уважаемый старик. Дизъюнкция высказываний истинна, если хотя бы
одно из высказываний истинно, следовательно: B * D B * C C * B 1 .
Один из подозреваемых совершил убийство, в то же время два других его не
совершали: B * C * D B * C * D B * C * D 1.
26.
Решение:Рассмотрим конъюнкцию построенных высказываний:
.
B * D B * C C * B * B * C * D B * C * D B * C * D 1
27.
Решение:3. минимизировать полученное выражение;
Упростим полученное выражение, исключая ложные высказывания:
B * D B * C C * B * B * C * D B * C * D B * C * D
B * D * B *C * D B * D * B *C * D B * D * B *C * D
B *C * B *C * D B *C * B *C * D B *C * B *C * D
C * B * B *C * D C * B * B *C * D C * B * B *C * D
B * D * B *C * D C * B * B *C * D
B *C * D C * B * D 1
28.
Решение:4. выбрать решение – набор значений простых высказываний, при которых
построенное логическое выражение является истинным;
Одно из высказываний должно быть истинно:
B *C * D C * B * D 1
29.
Решение:5. проверить, удовлетворяет ли полученное решение условию задачи.
Пусть истинным является выражение B * C * D , т.е. убийство совершил Смит. Но
тогда Браун – всеми уважаемый старик, так как оба раза сказал правду, и Джон
тоже – всеми уважаемый старик, так как оба раза сказал правду. Это
противоречит условию задачи.
Значит, истинным является выражение C * B * D , т.е. убийство совершил Браун.
Тогда Браун ничем не примечательный житель города, так как один раз сказал
правду, а один раз – солгал; Джон – мошенник, так как оба раза солгал, а Смит –
всеми уважаемый старик, так как оба раза сказал правду
Ответ:
Браун – убийца (ничем не примечательный житель города),
Джон мошенник,
Смит всеми уважаемый старик.
30.
Домашнее задание:решите с помощью логических операций.
1.В соревнованиях по гимнастике на первенство школы участвуют Алла, Валя, Таня
и Даша. Болельщики высказали предположения о возможных победителях: 1:
“Первой будет Таня, Валя будет второй”. 2: “Второй будет Таня, Даша - третьей”.
3: “Алла будет второй, Даша - четвертой”. По окончании соревнований оказалось,
что в каждом предположении только одно из высказываний истинно, другое же
ложно. Какое место на соревнованиях заняла каждая из девочек, если все они
оказались на разных местах?
2.Виктор, Роман, Юрий и Сергей заняли на математической олимпиаде первые 4
места. Когда их спросили о распределении мест, они дали три таких ответа:
1) Сергей – первый, Роман – второй
2) Сергей – второй, Виктор – третий
3) Юрий – второй, Виктор – четвёртый
Как распределились места, если в каждом утверждении только одно утверждение
истинно?
31.
3. Решитьлогическую
задачу.
Виновник
ночного
дорожно-транспортного
происшествия скрылся с места аварии. Первый свидетель сказал работникам ГАИ, что
это были "Жигули", первая цифра номера машины — единица. Второй свидетель сказал,
что машина была марки "Москвич", а номер начинался с семёрки. Третий свидетель
заявил, что машина была иностранная, номер начинался не с единицы. При дальнейшем
расследовании выяснилось, что каждый из свидетелей правильно указал либо только
марку машины, либо только первую цифру номера. Какой марки была машина и с какой
цифры начинался номер?
4. В соревнованиях по плаванию участвовали Андрей, Виктор, Саша и Дима. Их друзья
высказали предположения о возможных победителях:
1) первым будет Саша, Виктор будет вторым;
2) вторым будет Саша, Дима будет третьим;
3) Андрей будет вторым, Дима будет четвёртым.
По окончании соревнований оказалось, что в каждом из предположений только одно
из высказываний истинно, другое ложно. Какое место на соревнованиях занял каждый
из юношей, если все они заняли разные места.




























 Математика
Математика Информатика
Информатика








