Похожие презентации:
Плоскость в пространстве
1.
8.2. Плоскость в пространстве8.2.1. Некоторые понятия
n
q1
P
q2
Плоскость P
Нормальный вектор - любой
ненулевой вектор, ортогональный
этой плоскости: n ┴ P, |n| ≠ 0.
Направляющий вектор - любой
ненулевой вектор, параллельный
этой плоскости: q || P, |q| ≠ 0.
Плоскость можно задать одним n или
двумя неколлинеарными q1 и q2. Причем:
n = q1 x q2
Пусть n = (A, B, C), q1 = (l1, m1, n1), q2 = (l2, m2, n2). Тогда:
i
j k
n Ai Bj Ck ( A, B, C ) l1
m1
n1
l2
m2
n2
2.
8.2.2. Общее уравнение плоскостиУравнение плоскости, проходящей через точку M0(x0;y0;z0),
перпендикулярно вектору нормали n ( A, B, C )
n
Дано:
- плоскость P
- нормальный вектор n = (A, B, C)
M0
M
- фиксированная точка плоскости
M0(r0) = M0(x0, y0, z0).
- M(r) = M(x, y, z) лежит на P
n M 0 M 0 n (r r0 ) 0
nr nr0 0 nr D 0
O
- векторное уравнение плоскости
3.
То же самое для координат:n M 0 M 0 ( A, B, C ) ( x x0 , y y0 .z z0 ) 0
A( x x0 ) B( y y0 ) C ( z z0 ) 0 Ax By Cz D 0
Полное уравнение Ax+By+Cz+D = 0 <=> A, B, C, D — ненулевые.
Частные случаи:
(1) A = 0 => By + Cz + D = 0 или n = (0, B, C) - плоскость параллельна оси Ox.
(2) D = 0 => Ax + By + Cz = 0 - плоскость проходит через начало координат.
(3) A = 0, B = 0 => Cz + D = 0 или n = (0, 0, C) - плоскость параллельна Oxy.
(4) A = 0, B = 0, D = 0 => z = 0 - прямая совпадает с плоскостью Oxy.
Выводы:
1. Общее уравнение плоскости - линейное уравнение, коэффициенты
которого - координаты нормального вектора.
2. Если коэффициент отсутствует какая-либо координата, то плоскость
параллельна этой оси.
3. Если отсутствует свободный член, то плоскость проходит через начало
координат.
4.
8.2.3. Уравнение плоскости в отрезкахy
x
z
1
Ax+By+Cz+D = 0 полное =>
D/ A D/ B D/C
z
C ( 0,0, c )
B ( 0, b,0 )
y
x
x y z
1
a b c
A (a,0,0 )
a, b и c – отрезки, отсекаемые плоскостью на координатных
осях Ox, Oy и Oz соответственно.
Замечание: для частных случаев общего уравнения плоскости
уравнение плоскости в отрезках не существует.
5.
8.2.4. Нормальное уравнение плоскостиn (cos , cos , cos )
где α, β, γ - углы, образуемые
нормалью с осями координат.
O(0,0,0)
n
P0
p OP0 – расстояние от начала координат до плоскости
cosα · x + cosβ · y + cosγ · z + D = 0, (D = –
p)
6.
8.2.5. Уравнение плоскости , проходящей через точкупараллельно двум неколлинеарным векторам
Дано: M0(x0; y0; z0), a1 (m1; k1; l1 ), a2 (m2 ; k2 ; l2 )
a1
a2
M0
M
O
M M a a
0
1
2
0
x x0
y y0
z z0
m1
k1
l1
m2
k2
l2
0
7.
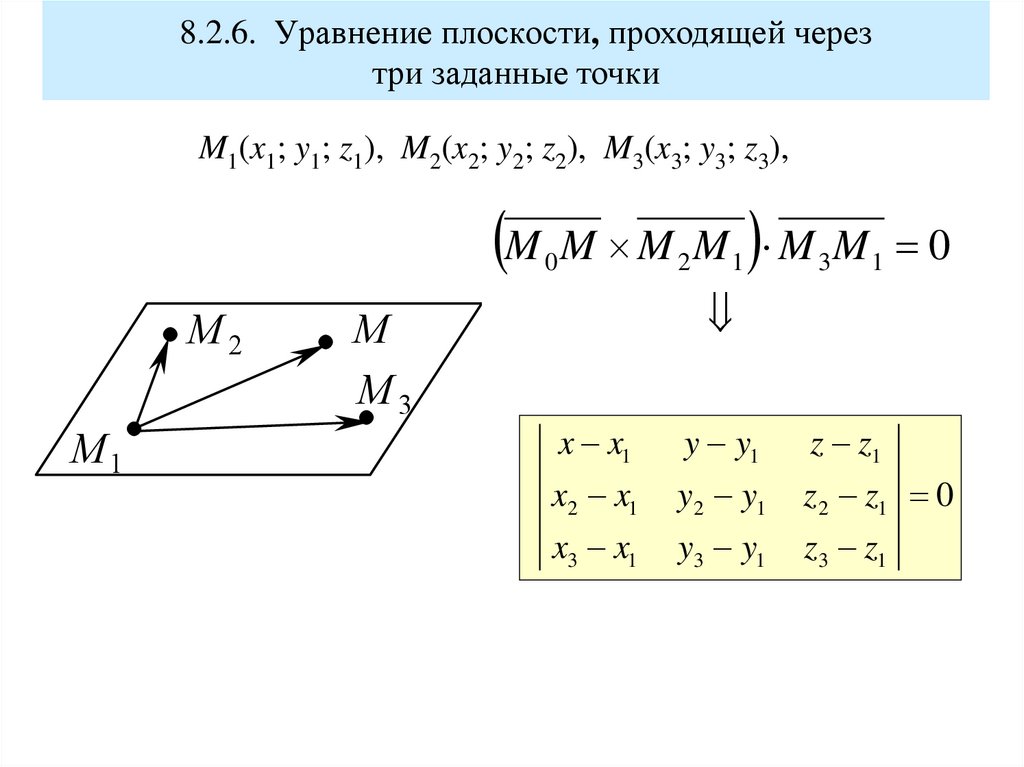
8.2.6. Уравнение плоскости, проходящей черезтри заданные точки
M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3),
M M M M M M
0
M2
M1
M
M3
2
1
3
1
0
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
8.
8.2.7. Взаимное расположение плоскостейP1: A1x + B1y + C1z + D1 = 0
P2: A2x + B2y + C2z + D2 = 0
n1 ( A1; B1; C1 ) – нормаль к P1 , n2 ( A2 ; B2 ; C2 ) – нормаль к P2
n1
P1
n1
n2
n2
A2
P1
P2
A1
P2
B1
B2
C1
C2
n1 n2
cos
n1 n2
P1 P2 n1 n 2 0
9.
8.2.8. Расстояние от точки до плоскостиДано: Ax + By + Cz + D = 0, M0(x0; y0; z0).
Найти: расстояние от точки M0 до плоскости.
n M 1M 0
d прn M 1M 0
n
( A, B, C ) ( x0 x1 , y0 y1 , z z0 )
A B C
2
2
2
Ax0 Ax1 By0 By1 Cz0 Cz1
A2 B 2 C 2
M0
n
d
M1
D
| Ax0 By0 Cz0 D |
| Ax0 By0 Cz0 Ax1 By1 Cz1 | d
2
2
2
A
B
C
A2 B 2 C 2
10.
8.2.9. Уравнение плоскости, проходящей через точкуДано: фиксированная точка плоскости M0(x0, y0, z0), вектор
нормали n = (A, B).
Найти: уравнение плоскости, проходящей через М0 и
перпендикулярной n.
Общее уравнение плоскости: Ax + By + Cz + D = 0
М0 лежит на плоскости => Ax0 + By0 + Cz0 + D = 0
=> A(x – x0) + B(y – y0) + C(z - z0) = 0
По другому: любой вектор M0M лежит в плоскости P =>
n M 0 M 0 A( x x0 ) B( y y0 ) C ( z z0 )
11.
Пример на нахождение уравнения плоскости через 3 точкиДано: три точки M1(1; 1; 1), M2(2; -1; 0), M3(0; 3; 0).
Найти: общее уравнение плоскости, проходящей через M1, M2, M3.
x x1
y y1
z z1
x2 x1
y2 y1
z2 z1 0
x3 x1
y3 y1
z3 z1
x 1
( x 1)
2
1
( y 1)
z 1
2 1 1 1 0 1 0
0 1
2 1
y 1
1
1
1 1
3 1
( z 1)
0 1
1
2
1
2
x 1 y 1 z 1
1
2
1 0
1
2
1
0
4( x 1) 2( y 1) 0 2( x 1) y 1 0 2 x y 3 0
12.
Пример на нахождение угла между плоскостямиДано: P1: 2x + 3y - 4z + 5 = 0, P2: y + 3 = 0
Найти: угол между P1 и P2.
n1 = (2; 4; -4) = (1; 2; -2),
cos
n2 = (0; 1; 0).
n1 n2 1 0 2 1 2 0 2
n1 n2
3
1 4 4 1
arccos
2
3
13.
Пример на нахождение уравнения плоскости через точкуДано: плоскость P: 5x - 4y + 2z + 1 = 0, точка M(2; 3; -1).
Найти: уравнение плоскости, проходящей через M
и параллельной P.
Первый способ:
Второй способ:
n1 = (5; -4; 2) = n2
A(x – x0) + B(y – y0) + C(z – z0) = 0
5x - 4y + 2z + D = 0
5(x – x0) – 4(y – y0) + 2(z – z0) = 0
5x0 - 4y0 + 2z0 + D = 0
5(x – 2) – 4(y – 3) + 2(z +1) = 0
5∙2 - 4 ∙ 3 + 2 ∙(-1) + D = 0
D=4
5x - 4y + 2z + 4 = 0
5x – 10 – 4y + 12 + 2z + 2 = 0
5x – 4y + 2z + 4 = 0
14.
Пример на нахождение расстояния между параллельными пл-миДано: P1: 4x - 2y + 4z + 5 = 0, P2: 2x - y + 2z - 7 = 0
Найти: расстояние между P1 и P2.
n1 = (4; -2; 4), n2 = (2; -1; 2) - коллинеарны.
Берём любую точку на P1 и вычисляем расстояние от неё до P2.
x = 0, y = 0 => z = -5/4 => M1(0; 0; -5/4).
d
d
| Ax0 By0 Cz0 D |
A2 B 2 C 2
| Ax1 By1 Cz1 D |
A B C
2
2
2
2 0 1 0 2 ( 5 / 4) 7
4 1 4
9,5 19
.
3
6













 Математика
Математика








