Похожие презентации:
Плоскость в пространстве. Прямая в пространстве
1. Лекция 11 Плоскость в пространстве. Прямая в пространстве
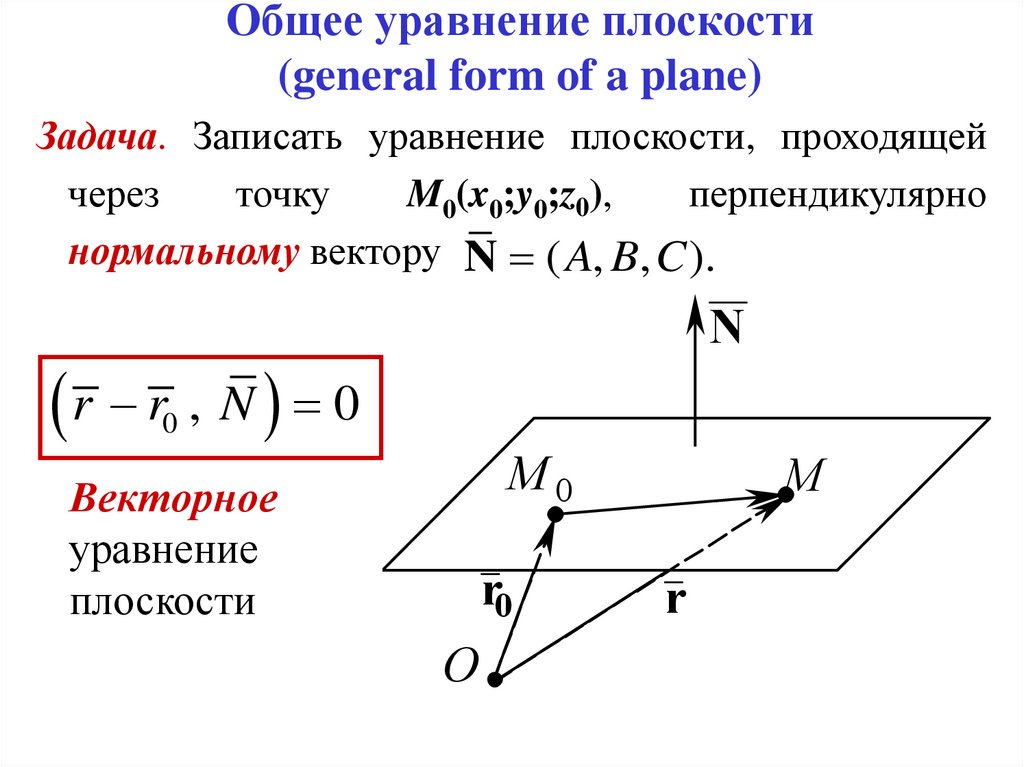
2. Общее уравнение плоскости (general form of a plane)
Задача. Записать уравнение плоскости, проходящейчерез
точку
M0(x0;y0;z0),
перпендикулярно
нормальному вектору N ( A, B, C ).
N
r r , N 0
0
M0
Векторное
уравнение
плоскости
r0
O
M
r
3.
r r , N 00
A( x x0 ) B( y y0 ) C ( z z0 ) 0;
Ax By Cz Ax0 By0 Cz0 0;
Ax By Cz D 0
где
A B C 0,
2
2
2
называется общим уравнением плоскости в
пространстве.
4. Исследование общего уравнения плоскости
Упр. Провести исследование общего уравненияплоскости в пространстве с построением
соответствующих эскизов.
Ax By Cz D 0
A B C 0.
2
2
2
Указание. По аналогии с исследованием общего
уравнения прямой на плоскости (лекция 10).
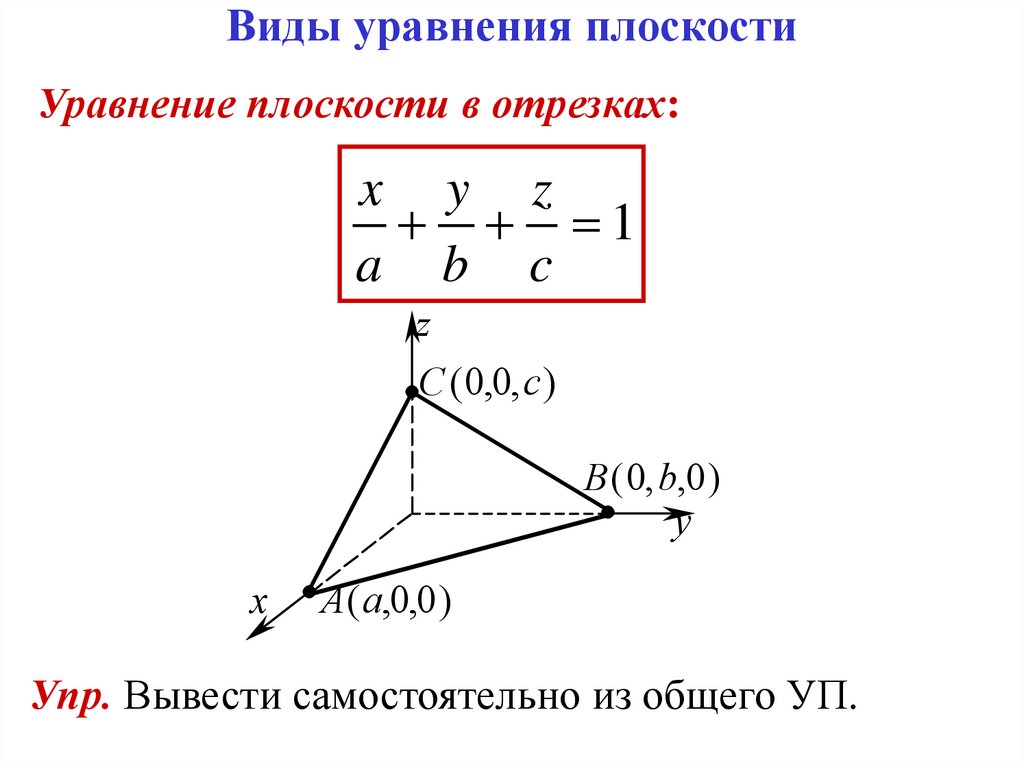
5. Виды уравнения плоскости
Уравнение плоскости в отрезках:x y z
1
a b c
z
C ( 0,0, c )
B ( 0, b,0 )
y
x
A (a,0,0 )
Упр. Вывести самостоятельно из общего УП.
6.
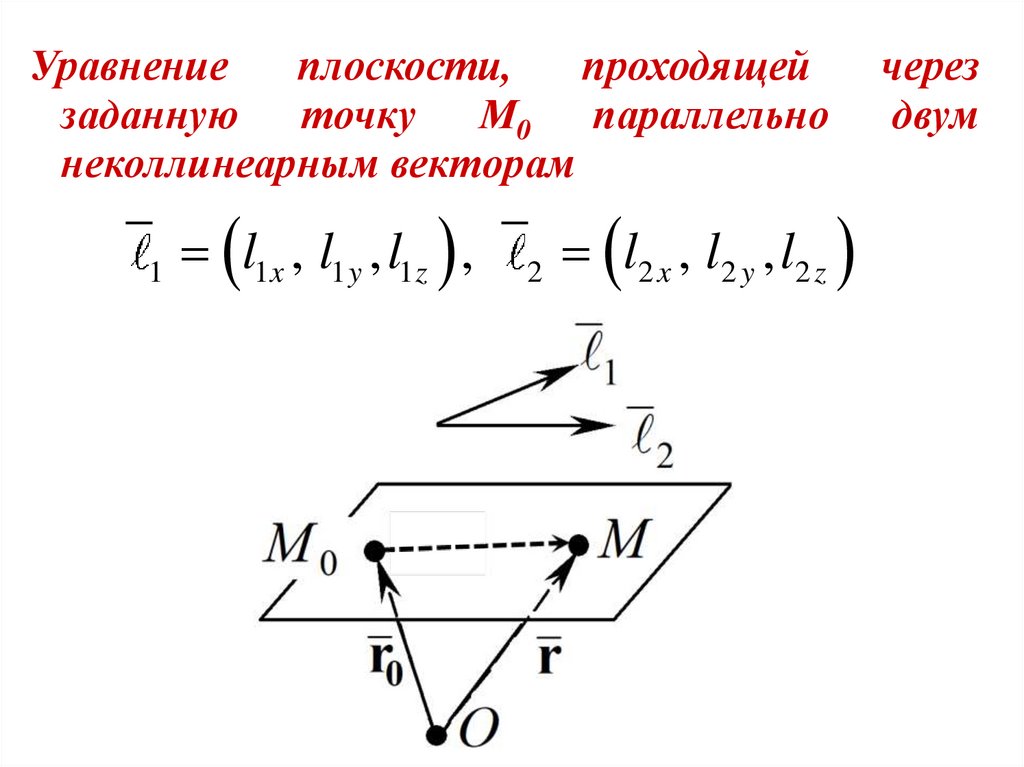
Уравнениеплоскости,
проходящей
заданную точку М0 параллельно
неколлинеарным векторам
1
l1x , l1 y , l1z ,
2
l2 x , l2 y , l2 z
через
двум
7.
r r ,0
1
,
2
0;
x x0
y y0
z z0
l1x
l2 x
l1 y
l2 y
l1z
l2 z
0
8.
Уравнение плоскости, проходящей через триточки, не лежащие на одной прямой
M2
M
M3
M1
r r1 , r2 r1 , r3 r1 0;
x x1
x2 x1
x3 x1
y y1
y2 y1
y3 y1
z z1
z2 z1 0.
z3 z1
9. Взаимное расположение плоскостей
В пространстве две плоскости могут: а) совпадать;а) быть параллельными; б) пересекаться.
Пусть плоскости λ1 и λ2 заданы общими
уравнениями:
λ1: A1x + B1y + C1z + D1 = 0
λ2: A2x + B2y + C2z + D2 = 0
Упр. Вывести самостоятельно соответствующие
критерии (по аналогии с прямыми на плоскости).
10.
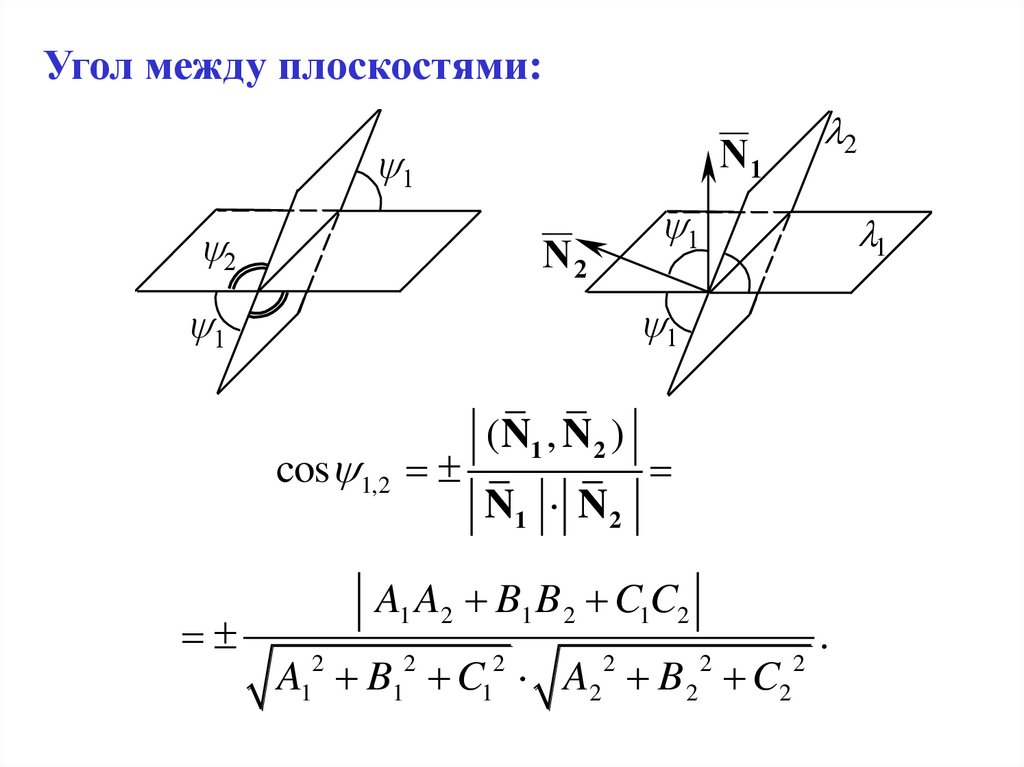
Угол между плоскостями:N1
1
2
1
N2
1
1
1
cos 1,2
2
(N1 , N 2 )
N1 N 2
A1 A2 B1 B 2 C1C2
A B C A2 B 2 C2
2
1
2
1
2
1
2
2
2
.
11. Расстояние от точки до плоскости
M0N
d
M1
d
Ax0 By0 Cz0 D
A B C
2
2
2
Упр. Доказать данную формулу (по аналогии с
расстоянием от точки до прямой на плоскости)
12.
Уравнения прямой в пространствеПусть A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0
– уравнения любых двух различных плоскостей,
содержащих прямую L . Тогда
A 1x B 1 y C 1z D 1 0 ,
A x B y C z D 0.
2
2
2
2
общее уравнение прямой в пространстве.
A1 x B1 y C 1 z D1
L:
A2 x B2 y C2 z D2
Должна быть 1
свободная
переменная!
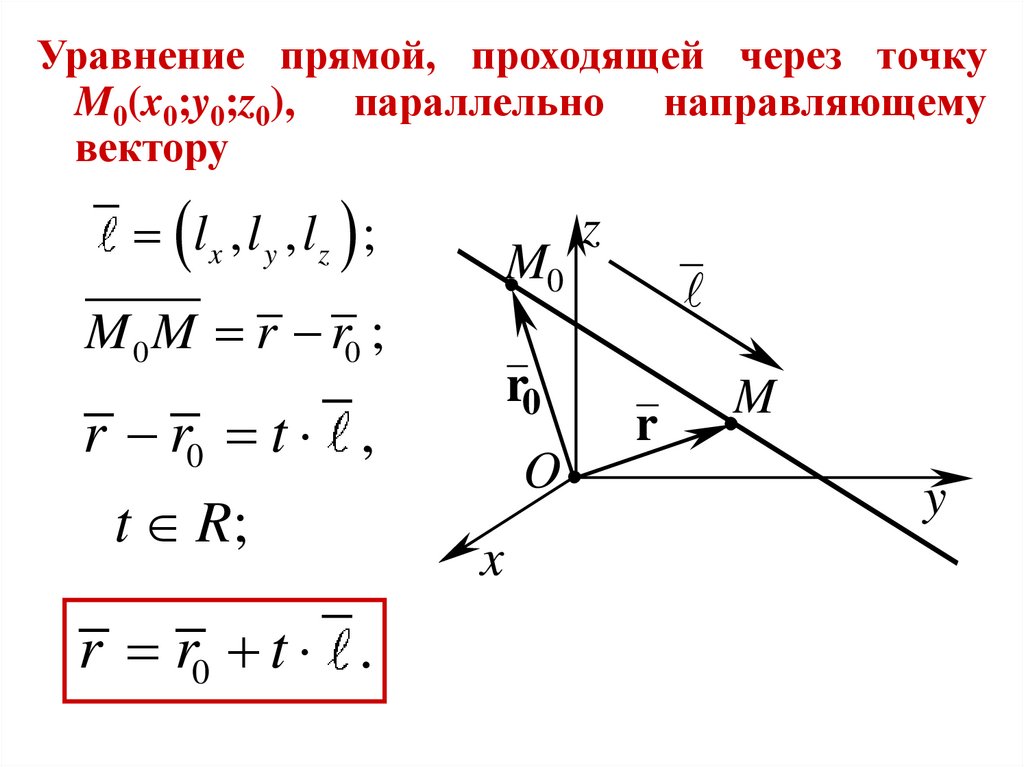
13.
Уравнение прямой, проходящей через точкуM0(x0;y0;z0), параллельно направляющему
вектору
lx , l y , lz ;
M0
M 0 M r r0 ;
r0
r r0 t ,
t R;
r r0 t .
O
x
z
r
M
y
14.
r r0 tx x0 t l x ,
y y0 t l y ,
z z0 t l z .
- параметрические уравнения прямой в
пространстве (в векторной и координатной
форме).
Пусть
lx 0 l y 0 lz 0
15.
x x0y y0
z z0
t
t
t
lx
ly
lz
x x0 y y0 z z0
lx
ly
lz
каноническое уравнение прямой в пространстве.
x x1
y y1
z z1
x2 x1 y2 y1 z2 z1
уравнение прямой в пространстве, проходящей
через 2 заданные точки.
16. Взаимное расположение прямых в пространстве
В пространстве две прямые могут:а) совпадать (to coincide);
б) быть параллельны (to be parallel);
в) пересекаться (to intersect);
г) скрещиваться (to skew).
L1 :
L2 :
x x1
l1x
x x2
l2 x
y y1
l1 y
y y2
l2 y
z z1
l1z
;
z z2
l2 z
.
17.
a) L1 L2 l2 l1 M 2 L1 ; R \{0};б) L1 || L2 l2 l1 M 2 L1 ; R \{0};
l2 x l2 y l2 z
l2 l1
; R \{0};
l
l
l
1y
1z
1x
18.
в)Прямые L1 и L2 пересекаются
2
M M ,
1
2
1
,
2
0 .
,
2
0 .
г) L1 и L2 скрещиваются
2
M M ,
1
2
1
19. Взаимное расположение прямой и плоскости в пространстве
Пусть в пространстве заданы плоскость λ и прямаяL. Они могут
1) быть параллельны;
2) прямая может лежать в плоскости;
3) пересекаться в одной точке.
: Ax By Cz D 0;
x x0 y y0 z z0
L:
.
lx
ly
lz
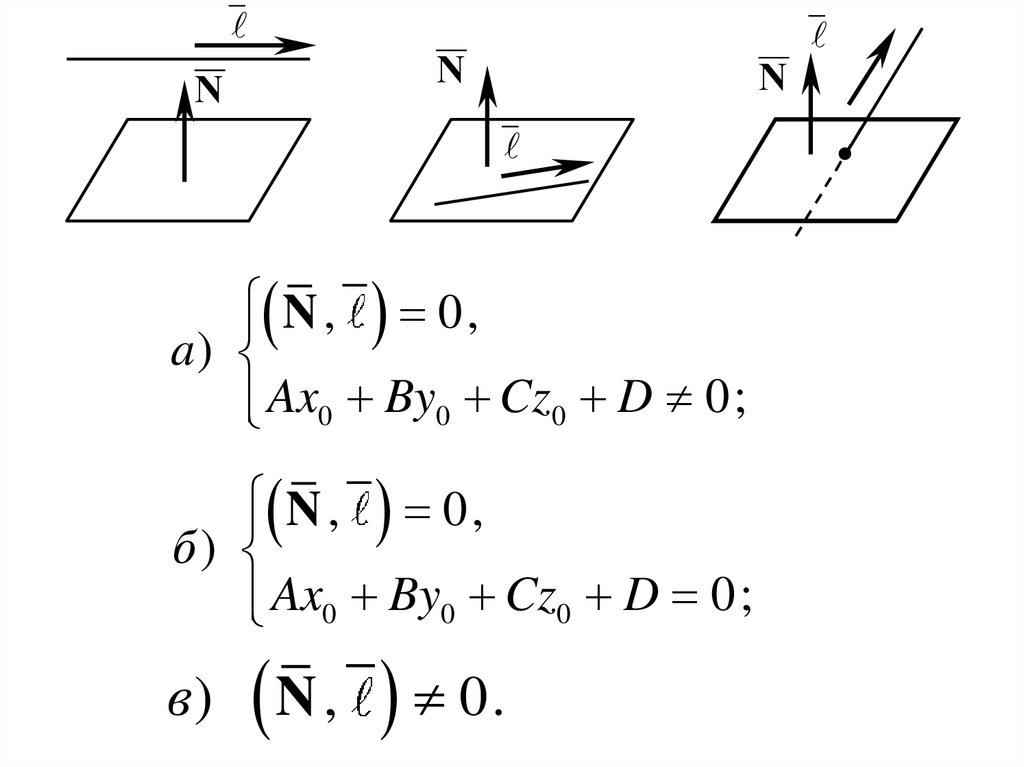
20.
NN
N
N , 0,
a)
Ax0 By0 Cz0 D 0;
N , 0,
б)
Ax0 By0 Cz0 D 0;
в) N ,
0.
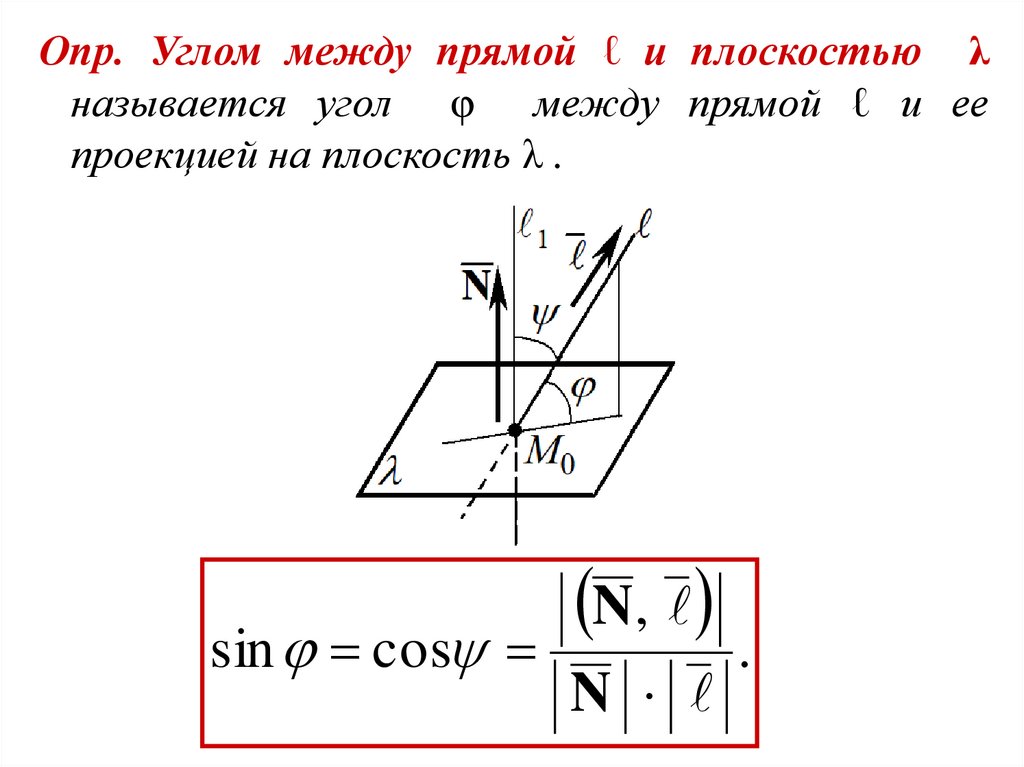
21.
Опр. Углом между прямой ℓ и плоскостью λназывается угол φ между прямой ℓ и ее
проекцией на плоскость λ .
sin cos
N,
N
.
22.
ЛЕКЦИЯ 12Типовые задачи аналитической
геометрии
в пространстве
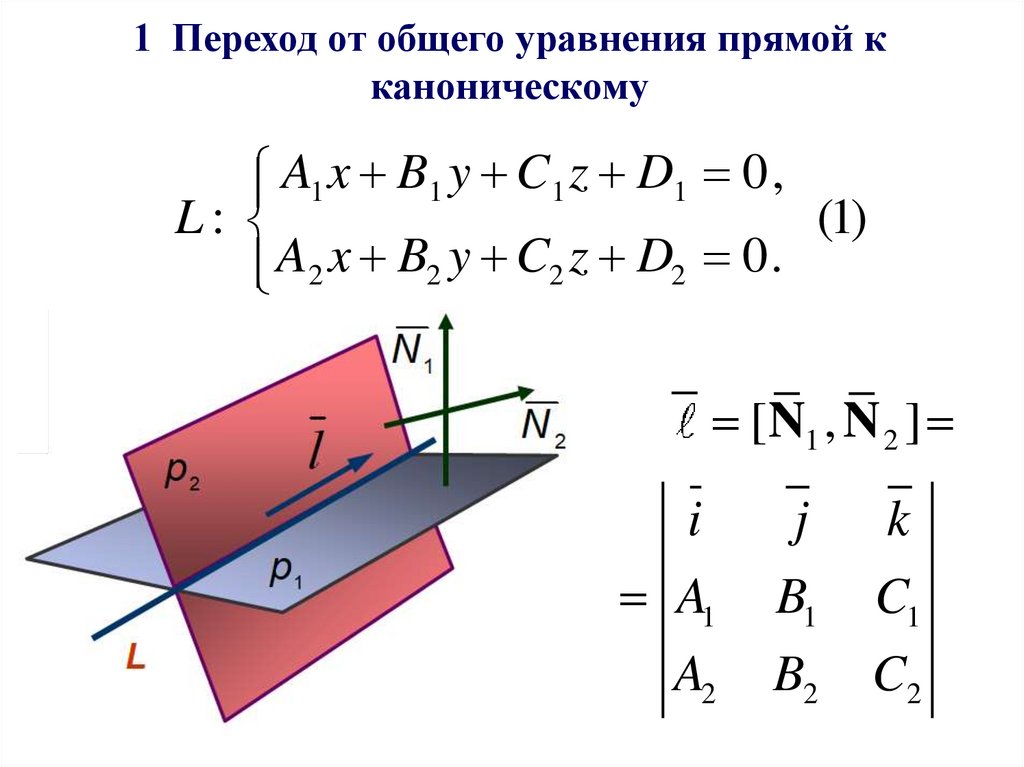
23. 1 Переход от общего уравнения прямой к каноническому
A1 x B1 y C 1 z D1 0,L:
(1)
A
x
B
y
C
z
D
0.
2
2
2
2
[N1 , N 2 ]
i
A1
A2
j
B1
B2
k
C1
C2
24.
Координаты точки M0 – это одно из решенийсистемы (1). Пусть z – свободная переменная.
Положим z0=0:
A1 x0 B1 y0 D1 ,
M 0 ( x0 , y0 , 0);
A
x
B
y
D
.
2
0
2
0
2
x x0 y y0 z z0
L:
.
lx
ly
lz
Упр. Написать каноническое ур-е прямой:
2 x 3 y z 2 0
x 11 y 8 z
. Отв.
4
3
1
x y z 3 0
25.
2. Плоскость β, проходящая через даннуюточку М0 параллельно данной плоскости α
M 0 M x x0 , y y0 , z z0 ;
26.
N, M M 00
A x x0 B y y0 C z z0 0.
Упр. Плоскость, проходящая через точку (2; -1;
6) и параллельная плоскости x + y - 2z + 5 = 0.
Ответ: x + y - 2z + 11 = 0
27.
3. Плоскость Р, проходящая через две точкиМ0 и М1 перпендикулярно данной плоскости
Аx+By+Cz+D=0:
M M , M M , N 0;
0
0
1
Упр. Плоскость, проходящая через две точки
М0(1; 2; 3) и М1(2; 1; 1) перпендикулярно
плоскости 3х + 4у + z - 6 = 0.
Ответ: x - y + z - 2 = 0.
28.
4. Плоскость Р, проходящая через даннуюточку М0 перпендикулярно двум
пересекающимся плоскостям Q1 и Q2
M M , N , N 0;
0
1
2
Упр. Плоскость, проходящая через точку (1; 3;
2) и перпендикулярная плоскостям х + 2у + z - 4
= 0 и 2х + у + 3z + 5 = 0.
Ответ: 5x - y - 3z + 4 = 0.
29.
5. Уравнение плоскости P, проходящей черезданную точку M0 перпендикулярно данной
прямой L
N l lx , l y , lz ;
l, M M 0.
0
lx x x0 l y y y0 lz z z0 0
30.
Упр. Плоскость, проходящая через точку(-1; -5; 8) и перпендикулярная прямой
x y z 3
.
0 2
5
Ответ: 2y + 5z - 30 = 0.
31.
6. Уравнение прямой, проходящей черезданную точку М0 перпендикулярно данной
плоскости Аx + By + Cz + D = 0
x x0 y y0 z z0
.
A
B
C
Упр. Прямая, проходящая через начало
координат и перпендикулярная плоскости
3х + 5z - 5 = 0.
x y z
.
Ответ:
3 0 5
32.
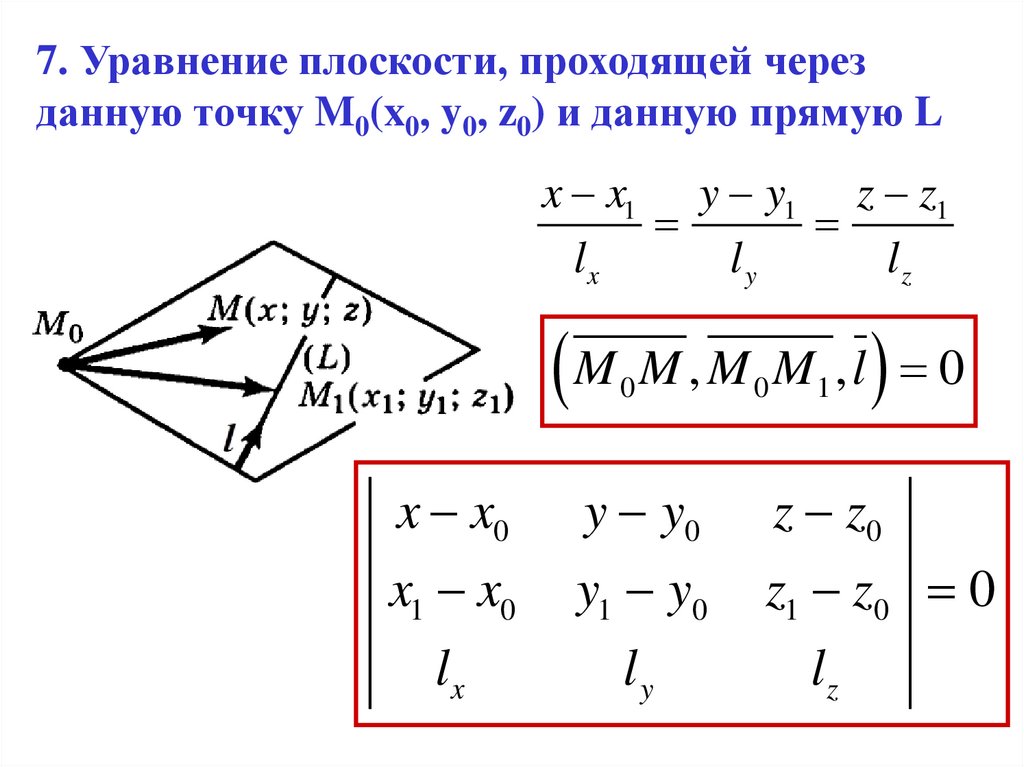
7. Уравнение плоскости, проходящей черезданную точку M0(x0, y0, z0) и данную прямую L
x x1 y y1 z z1
lx
ly
lz
M M , M M ,l 0
0
x x0
x1 x0
lx
y y0
y1 y0
ly
0
1
z z0
z1 z0 0
lz
33.
Упр. Плоскость, проходящая через точкуМ0(5,2,3) и прямую
Ответ: x - 2y - 1 = 0.
34.
8. Уравнение плоскости, проходящей черезданную точку M0 и параллельной двум
неколлинеарным прямым L1 и L2:
M M ,l ,l 0
0
1
2
x x0
y y0
z z0
l1x
l2 x
l1 y
l2 y
l1z
l2 z
0
35.
9. Уравнение плоскости, проходящей черезданную прямую L1 и параллельной другой
данной прямой L2
x x1
y y1
z z1
l1x
l2 x
l1 y
l2 y
l1z
l2 z
0,
где (x1, y1, z1) - координаты какой-либо точки
М1 прямой L1.
Упр. Сделать рисунок и доказать формулу.
36.
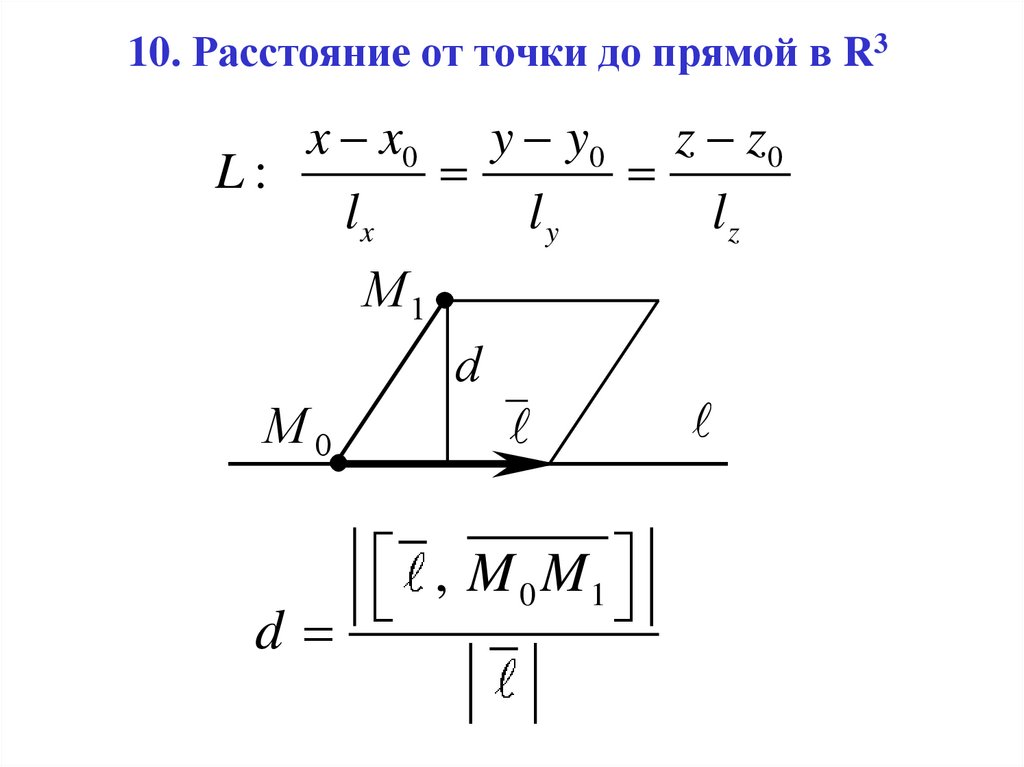
10. Расстояние от точки до прямой в R3x x0 y y0 z z0
L:
lx
ly
lz
M1
d
M0
d
, M 0 M1
37.
11. Расстояние между скрещенными прямымиОпр. Расстоянием между двумя скрещивающимися
прямыми
называется
длина
их
общего
перпендикуляра.
M2
d
2
d
M1
1
1
2
d
Ax 2 By 2 Cz 2 D
2
2
A B C
2
где Ax+By+Cz+D = 0 – общее уравнение плоскости λ,
M2(x2; y2; z2) – любая точка на прямой ℓ2.
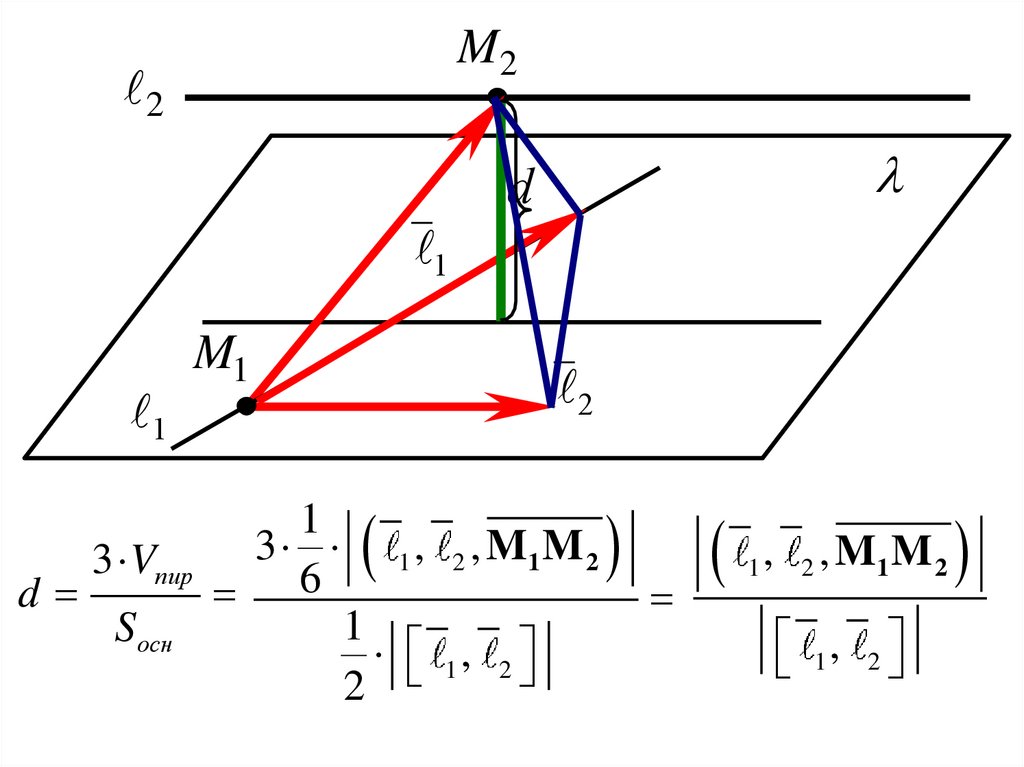
38.
M22
d
1
1
M1
2
1
3 Vпир 3 6 1 , 2 , M1 M 2
d
1
Sосн
1 , 2
2
, ,M M
1
2
1
1 , 2
2
39.
12. Нахождение точки пересечения прямых в R3Пусть M0(x0;y0;z0) – точка пересечения прямых.
Тогда (x0;y0;z0) – решение системы уравнений
x x1 t m1 ,
x x1 y y1 z z1
y y1 t n1 ,
,
m
n
p
1
1
1
z z1 t p1 ,
x
x
m
,
x
x
y
y
z
z
2
2
2
2
2
,
y y2 n2 ,
m2
n2
p2
z z2 p2 .
Упр. Исследовать систему уравнений в общем виде
на предмет совместности и определенности.











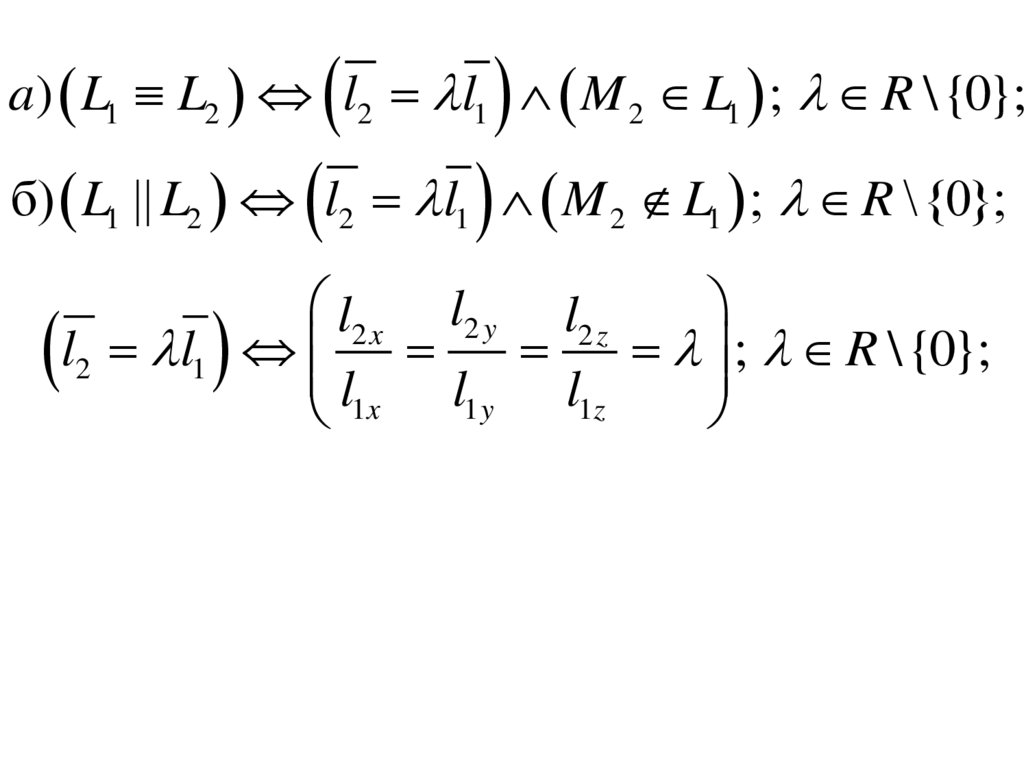
















 Математика
Математика








