Импульсные, цифровые и дискретные САР. Устойчивость дискретных систем. Лекция 13

1.

РАДИОАВТОМАТИКА
Лекция 13
ИМПУЛЬСНЫЕ, ЦИФРОВЫЕ И
ДИСКРЕТНЫЕ САР.
УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ
СИСТЕМ

2. ИМПУЛЬСНЫЕ, ЦИФРОВЫЕ И ДИСКРЕТНЫЕ САР

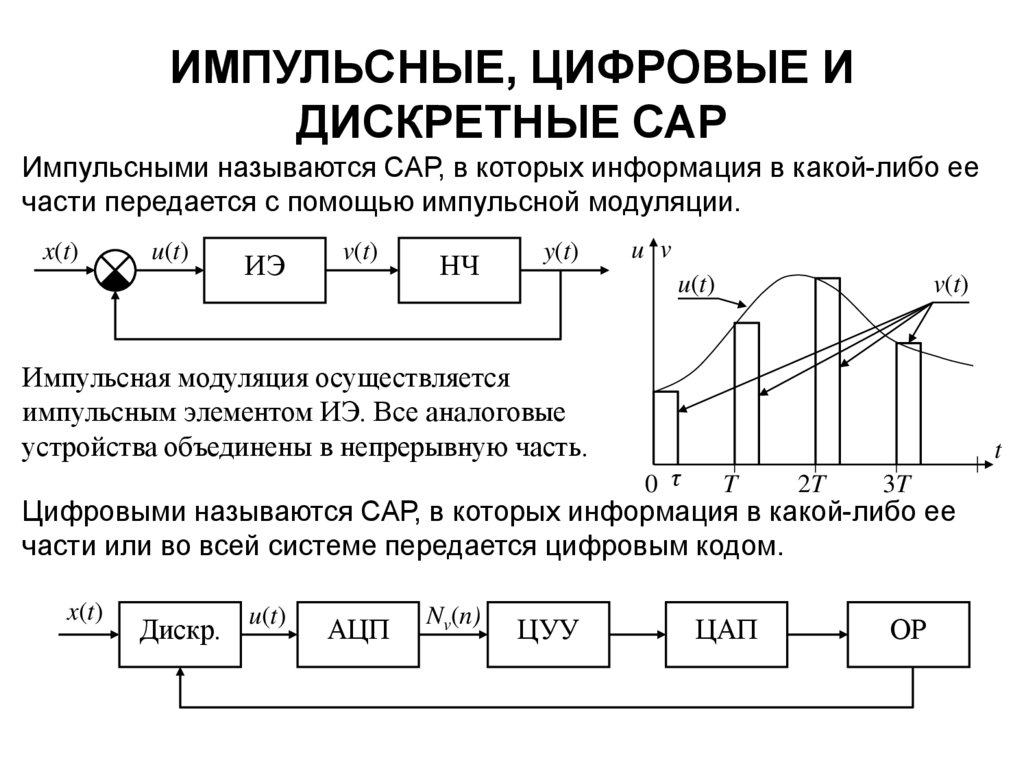
Импульсными называются САР, в которых информация в какой-либо ее
части передается с помощью импульсной модуляции.
x(t)
u(t)
ИЭ
v(t)
НЧ
y(t)
u v
v(t)
u(t)
Импульсная модуляция осуществляется
импульсным элементом ИЭ. Все аналоговые
устройства объединены в непрерывную часть.
0 τ
t
T
2T
3T
Цифровыми называются САР, в которых информация в какой-либо ее
части или во всей системе передается цифровым кодом.
x(t)
Дискр.
u(t)
АЦП
Nv(n)
ЦУУ
ЦАП
ОР

3.

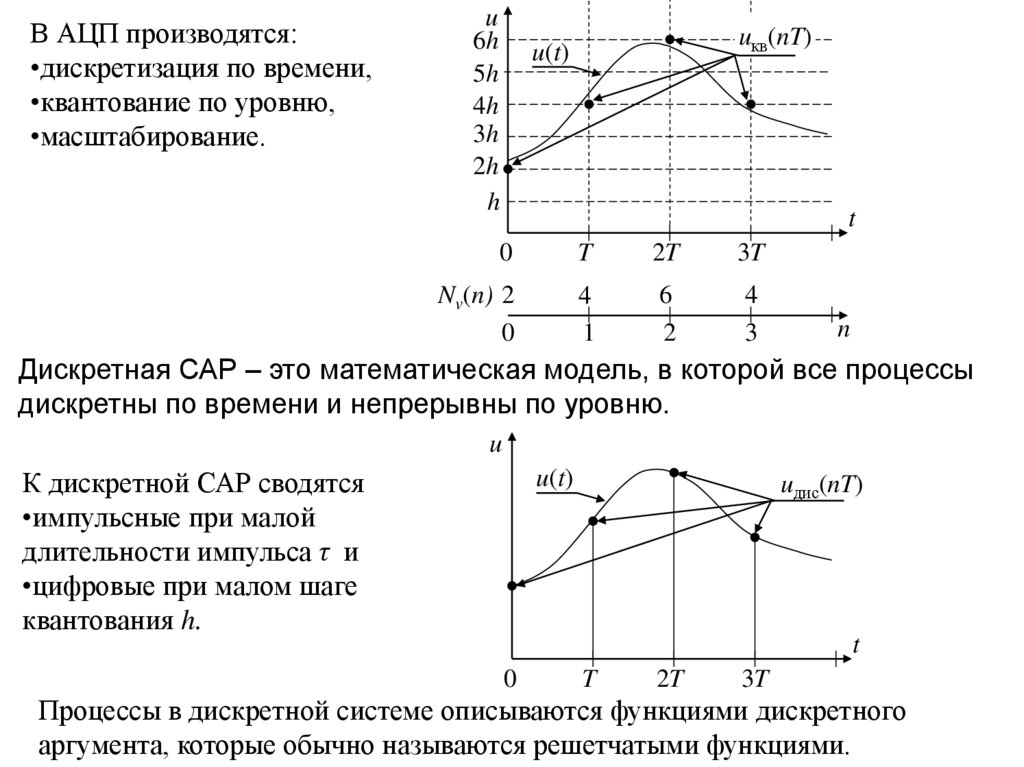
В АЦП производятся:
•дискретизация по времени,
•квантование по уровню,
•масштабирование.
u
6h
5h
4h
3h
2h
h
uкв(nT)
u(t)
t
0
T
2T
3T
Nv(n) 2
0
4
1
6
2
4
3
n
Дискретная САР – это математическая модель, в которой все процессы
дискретны по времени и непрерывны по уровню.
u
К дискретной САР сводятся
•импульсные при малой
длительности импульса τ и
•цифровые при малом шаге
квантования h.
u(t)
uдис(nT)
t
0
T
2T
3T
Процессы в дискретной системе описываются функциями дискретного
аргумента, которые обычно называются решетчатыми функциями.

4. РЕШЕТЧАТЫЕ ФУНКЦИИ, РАЗНОСТИ, РАЗНОСТНЫЕ УРАВНЕНИЯ

– x[nT]
x
Δt
0
Δt
T
Δt
2T
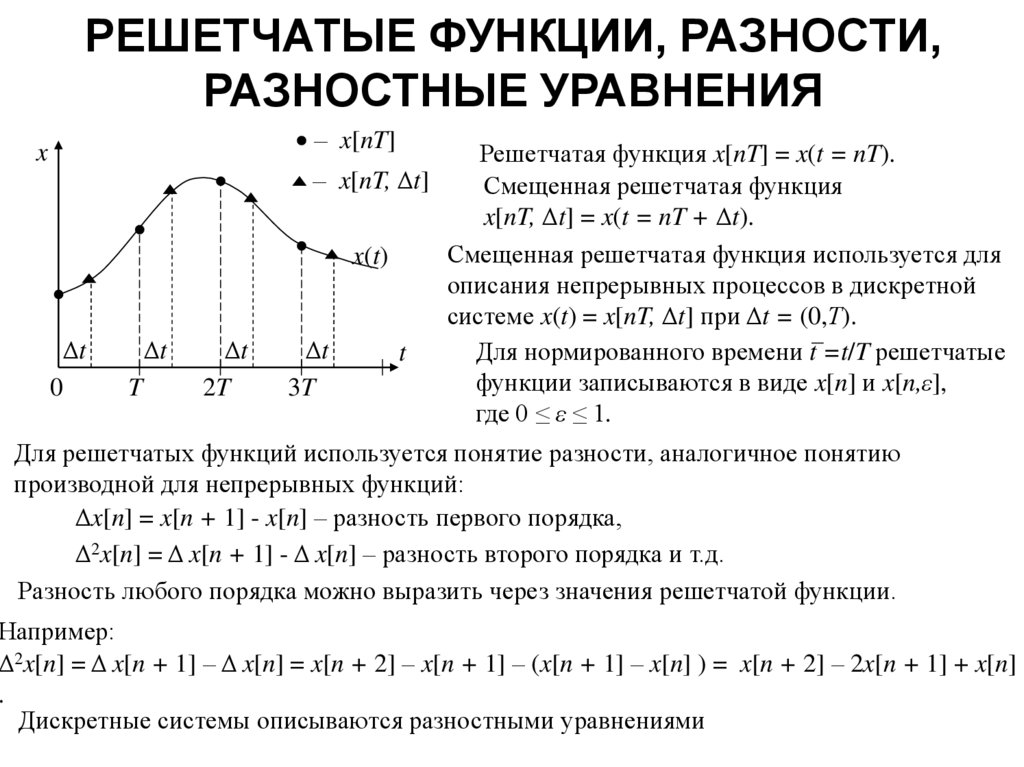
Решетчатая функция x[nT] = x(t = nT).
– x[nT, Δt]
Смещенная решетчатая функция
x[nT, Δt] = x(t = nT + Δt).
Смещенная решетчатая функция используется для
x(t)
описания непрерывных процессов в дискретной
системе x(t) = x[nT, Δt] при Δt = (0,Т).
Δt
Для нормированного времени t =t/T решетчатые
t
функции записываются в виде x[n] и x[n,ε],
3T
где 0 ≤ ε ≤ 1.
Для решетчатых функций используется понятие разности, аналогичное понятию
производной для непрерывных функций:
Δx[n] = x[n + 1] - x[n] – разность первого порядка,
Δ2x[n] = Δ x[n + 1] - Δ x[n] – разность второго порядка и т.д.
Разность любого порядка можно выразить через значения решетчатой функции.
Например:
Δ2x[n] = Δ x[n + 1] – Δ x[n] = x[n + 2] – x[n + 1] – (x[n + 1] – x[n] ) = x[n + 2] – 2x[n + 1] + x[n]
.
Дискретные системы описываются разностными уравнениями

5.

Используются две формы записи разностных уравнений:
каноническая
amΔmy[n] + am-1Δm-1y[n] + … + a0y[n] = bl Δlx[n] + bl-1 Δl-1x[n] + … +b0 x[n]
и рекуррентная
dmy[n + m] + dm-1y[n + m – 1] + … + d0y[n] = cl x[n + l] + cl-1 x[n + l – 1] + … +c0 x[n]
К решетчатым функциям применимы преобразования Фурье и Лапласа в форме
дискретных преобразований
D-преобразование: D{x[n]} = x n e
n 0
Z-преобразование: Z{x[n]} =
nq
x[n]z
n
=X(q), где q=pT – комплексная переменная.
=X(z), где z = eq.
n 0
Отношение Z-преобразований выходной и входной переменных называется дискретной
передаточной функцией K(z).
Z{dmy[n + m] + dm-1y[n + m – 1] + … + d0y[n] = cl x[n + l] + cl-1 x[n + l – 1] + … +c0 x[n]}
Учитывая свойство Z-преобразования: Z{x[n + k]} = zk X(z), получим:
dmzmY(z) + dm-1zm-1Y(z) + … +d0Y(z) = clzlX(z) + cl-1zl- 1X(z) + … +c0X(z) .
Тогда K(z) =
clzl + cl-1zl- 1 + … + c0
dmzm + dm-1zm-1 +… + d0

6. УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ СИСТЕМ

x[n]
K(z)
y[n]
Определим устойчивость непосредственно по решению
разностного уравнения: система устойчива, если при
ограниченном входном процессе x[n] выходной процесс y[n]
тоже ограничен
dmy[n + m] + dm-1y[n + m – 1] + … + d0y[n] = cl x[n + l] + cl-1 x[n + l – 1] + … +c0 x[n].
Решение y[n] = yсв[n] + yприн[n].
Принужденная составляющая определяется правой частью уравнения и при
ограниченном входном процессе тоже будет ограниченной. Поэтому неограниченной
может быть свободная составляющая, которая является решением однородного
разностного уравнения
dmy[n + m] + dm-1y[n + m – 1] + … + d0y[n] = 0.
Решение записывается в виде суммы степенных функций zin: yсв[n] =
где zi – корни характеристического уравнения
dmzm + dm-1zm -1+ … + d0 = 0.
m
Az
i 1
n
i i
,
m
Система устойчива, если lim
n
n
A
z
i i 0.
Откуда | zi | < 1.
i 1
Линейная дискретная система устойчива, если все корни
характеристического уравнения лежат внутри окружности
единичного радиуса.

7. КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА

Чтобы воспользоваться критерием Гурвица, сформулированным
для непрерывных систем, нужно внутренность окружности
единичного радиуса отобразить в левую полуплоскость
1+w
Это делается билинейным преобразованием z =
.
1
–
w
R=∞
Im
Im
Z
W
Re
-1
0
1
Re
-1
dmzm + dm-1zm -1+ … + d0 =
m 1
0. 1 w m
1
w
dm
d m 1
... d 0 0.
1 w
1 w
d m wm d m 1wm 1 ... d 0 0
0
d m 1
d m 3
d m
d m 2
d m 5
d m 4
0
0
0
0 0
d m 1
d m 3
d 0