Похожие презентации:
Колебательные цепи при гармонических воздействиях. Лекция 5
1.
Лекция № 5Колебательные цепи при гармонических
воздействиях. Последовательный и
параллельный колебательные контуры.
Входные и передаточные функции
последовательного контура.
Oscillatory circuits under harmonic influences.
Serial and parallel oscillating circuits. Input and
transfer functions of a sequential circuit.
2.
Как известно, простейшими резонансными (или колебательными)
цепями являются последовательный и параллельный колебательные
контуры. Рассмотрим цепь, состоящую из последовательно включенных
катушки индуктивности и конденсатора. При воздействии на цепь,
состоящую из последовательно включенных катушки индуктивности и
конденсатора, переменного напряжения, через катушку и конденсатор будет
протекать переменный ток.
As you know, the simplest resonant (or oscillatory) circuits are serial and
parallel oscillatory circuits. Consider a circuit consisting of a series-connected
inductor and a capacitor. When an alternating voltage is applied to a circuit
consisting of a series-connected inductor and capacitor, an alternating current
will flow through the coil and capacitor.
2
3.
• Зависимости реактивных сопротивлений катушки XL иконденсатора ХC от круговой частоты ω
• Dependence of the reactivities of the coil XL and the capacitor ХC
on the circular frequency ω
3
4.
Параметры колебательного контураParameters of the oscillating circuit
• Одними из наиболее важных параметров колебательного
контура (кроме, разумеется, резонансной частоты) являются
его характеристическое сопротивление ρ и добротность Q.
Характеристическим сопротивлением контура ρ называется
величина модуля реактивного сопротивления емкости и
индуктивности контура на резонансной частоте:
ρ = |ХL| =|ХC| при ω =ωр.
• One of the most important parameters of an oscillating circuit
(except, of course, the resonant frequency) is its characteristic
resistance ρ and Q-factor. the Characteristic resistance of the
circuit ρ is the value of the reactance modulus of the capacitance
and inductance of the circuit at the resonant frequency: ρ = |ХL|
=|ХC| at ω =ωр.
4
5.
СопротивлениеResistance
• В общем случае характеристическое сопротивление может
быть вычислено следующим образом: ρ = √(LC).
Характеристическое
сопротивление
ρ
является
количественной мерой оценки энергии, запасенной
реактивными элементами контура – катушкой (энергия
магнитного поля) WL= (LI2)/2 и конденсатором (энергия
электрического поля) WC=(CU2)/2.
• In General, the characteristic resistance can be calculated as
follows: ρ = √(LC). The characteristic resistance ρ is a
quantitative measure of the energy stored by the reactive elements
of the circuit – the coil (magnetic field energy) WL= (LI2)/2 and
the capacitor (electric field energy) WC=(CU2)/2.
5
6.
Добротность контураQ of the circuit
• Отношение энергии, запасенной реактивными элементами
контура, к энергии омических (резистивных) потерь за период
принято называть добротностью Q контура, что в
буквальном переводе с английского языка обозначает
«качество».
• The ratio of the energy stored by the reactive elements of the
circuit to the energy of ohmic (resistive) losses over the period is
called the Q-factor of the circuit, which literally means «quality»
in English.
6
7.
• Величину, обратную добротности d=1/Q называютзатуханием контура. Для определения добротности обычно
пользуются формулой Q=ρ/r, где r-сопротивление омических
потерь контура, характеризующее мощность резистивных
(активных потерь) контура Р=I2r.
• The inverse of the Q-factor d=1/Q is called contour
attenuation. To determine the quality factor, the formula Q=ρ/r is
usually used, where r is the resistance of the ohmic losses of the
circuit, which characterizes the power of the resistive (active
losses) of the circuit Р=I2r.
7
8.
• Частотные свойства различных цепей в технике принятооценивать с помощью амплитудно-частотных характеристик
(АЧХ). На рисунках представлены два простейших
четырехполюсника,
содержащих
последовательный
колебательный контур.
• The frequency properties of various circuits in engineering are
usually evaluated using the amplitude-frequency characteristics
(AFC). For figure shows two simple four-pole circuits containing
a sequential oscillating circuit.
8
9.
• На частотах, сильно отличающихся от резонансной,сопротивление контура переменному току достаточно велико,
а следовательно, и коэффициент передачи цепи будет падать
практически до нуля.
• At frequencies that are very different from the resonant one, the
resistance of the circuit to alternating current is quite high, and
therefore the transmission coefficient of the circuit will fall to
almost zero.
9
10.
• Свойство колебательного контура выделять из множествачастот одну принято называть селективностью или
избирательностью.
• The property of an oscillating circuit to select one of the many
frequencies is called selectivity or selectivity.
• При этом интенсивность изменения коэффициента
передачи цепи при отстройке частоты воздействия от
резонанса принято оценивать при помощи параметра,
называемого полосой пропускания.
• In this case, the intensity of the change in the transmission
coefficient of the circuit when the frequency of the impact is
detuned from the resonance is usually estimated using a parameter
called the bandwidth.
10
11.
• При расширении полосы пропускания цепи ухудшаются ееселективные (избирательные) свойства. Исходя из этого, при расчете и
конструировании колебательных контуров нужно стремиться к
повышению их добротности.Однако, в ряде случаев, добротность контура,
наоборот, приходится занижать (например, включая последовательно с
катушкой индуктивности резистор небольшой величины сопротивления),
что позволяет избежать искажений широкополосных сигналов.
• When the bandwidth of the circuit is expanded, its selective properties
deteriorate. Based on this, when calculating and designing oscillating circuits,
one should strive to increase their q-factor. However, in some cases, the q-factor
of the circuit, on the contrary, has to be underestimated (for example, including
a small resistor in series with the inductor), which avoids distortion of
broadband signals.
11
12.
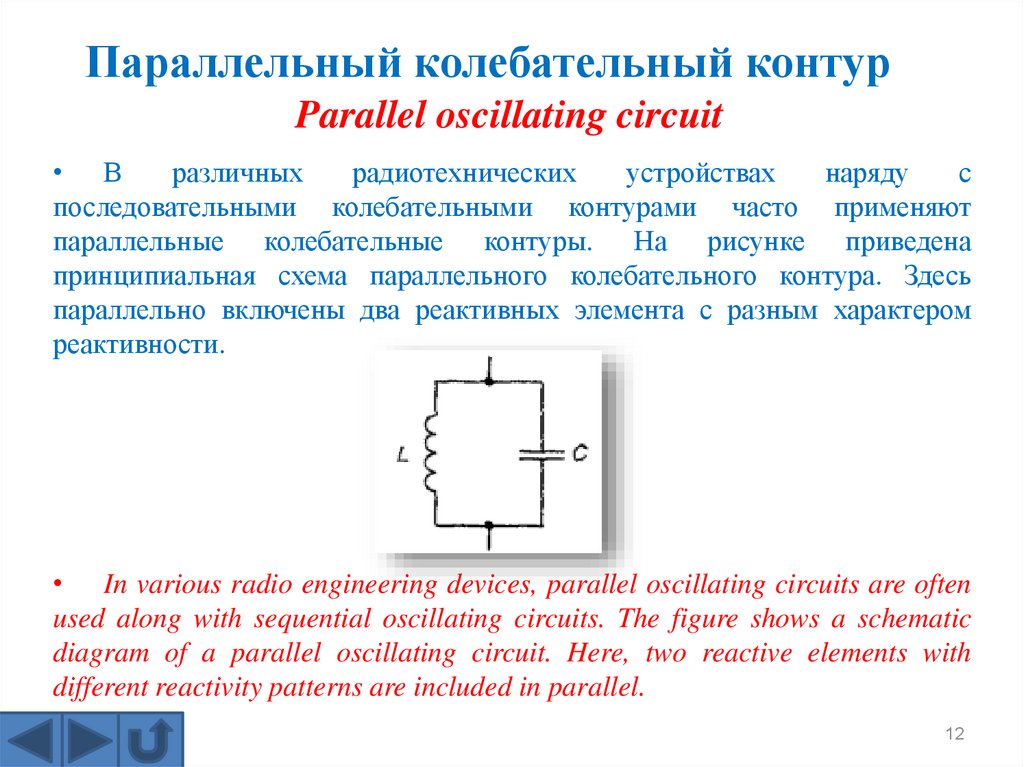
Параллельный колебательный контурParallel oscillating circuit
• В
различных
радиотехнических
устройствах
наряду
с
последовательными колебательными контурами часто применяют
параллельные колебательные контуры. На рисунке приведена
принципиальная схема параллельного колебательного контура. Здесь
параллельно включены два реактивных элемента с разным характером
реактивности.
• In various radio engineering devices, parallel oscillating circuits are often
used along with sequential oscillating circuits. The figure shows a schematic
diagram of a parallel oscillating circuit. Here, two reactive elements with
different reactivity patterns are included in parallel.
12
13.
• Аналогично, как и для последовательного колебательногоконтура, имеется некоторая частота, называемая резонансной,
на которой реактивные сопротивления катушки и
конденсатора одинаковы.
• Similarly, as for a series oscillating circuit, there is a certain
frequency, called resonant, at which the reactivities of the coil and
the capacitor are the same.
• На этой частоте суммарная проводимость параллельного
колебательного контура без потерь обращается в нуль. Это
значит, что на этой частоте колебательный контур обладает
бесконечно большим сопротивлением переменному току.
• At this frequency, the total conductivity of the parallel
oscillating circuit without loss vanishes. This means that at this
frequency, the oscillating circuit has an infinitely large resistance
to alternating current.
13
14.
Зависимость реактивногосопротивления контура от частоты
Dependence of the loop's reactance on
frequency
• На частотах, отличных от резонансной, сопротивление контура
уменьшается и приобретает реактивный характер на более низких
частотах – индуктивный, а на более высоких – наоборот, емкостной.
• At frequencies other than resonant, the loop resistance decreases and
becomes reactive at lower frequencies – inductive, and at higher frequencies –
on the contrary, capacitive.
14
15.
Процесс работы контураThe process of operation of the circuit
• В процессе работы контура, дважды за период колебаний, происходит
энергетический обмен между катушкой и конденсатором. Энергия
поочередно накапливается то в виде энергии электрического поля
заряженного конденсатора, то в виде энергии магнитного поля катушки
индуктивности.
• During the operation of the circuit, twice during the oscillation period, an
energy exchange occurs between the coil and the capacitor. The energy is
alternately accumulated in the form of the electric field energy of a charged
capacitor, then in the form of the magnetic field energy of the inductor.
15
16.
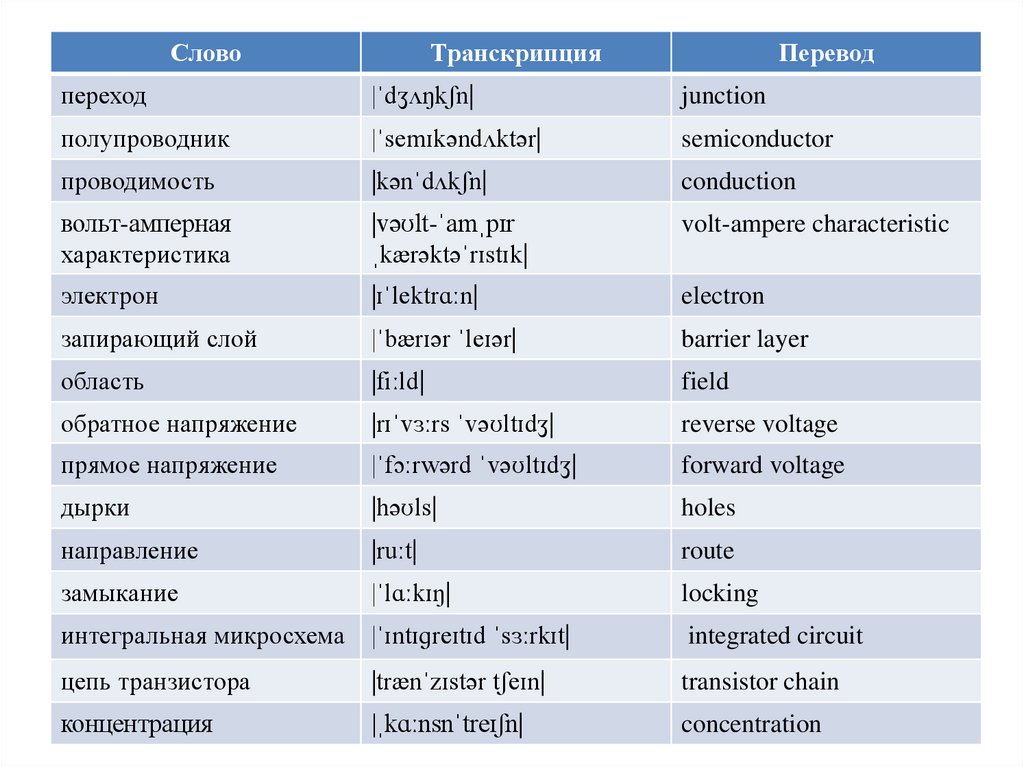
СловоТранскрипция
Перевод
переход
|ˈdʒʌŋkʃn|
junction
полупроводник
|ˈsemɪkəndʌktər|
semiconductor
проводимость
|kənˈdʌkʃn|
conduction
вольт-амперная
характеристика
|vəʊlt-ˈamˌpɪr
ˌkærəktəˈrɪstɪk|
volt-ampere characteristic
электрон
|ɪˈlektrɑːn|
electron
запирающий слой
|ˈbærɪər ˈleɪər|
barrier layer
область
|fiːld|
field
обратное напряжение
|rɪˈvɜːrs ˈvəʊltɪdʒ|
reverse voltage
прямое напряжение
|ˈfɔːrwərd ˈvəʊltɪdʒ|
forward voltage
дырки
|həʊls|
holes
направление
|ruːt|
route
замыкание
|ˈlɑːkɪŋ|
locking
интегральная микросхема
|ˈɪntɪɡreɪtɪd ˈsɜːrkɪt|
integrated circuit
цепь транзистора
|trænˈzɪstər tʃeɪn|
transistor chain
концентрация
|ˌkɑːnsnˈtreɪʃn|
concentration
16














 Физика
Физика Английский язык
Английский язык








