Похожие презентации:
Квадратный корень из произведения и дроби
1.
1. Арифметическим квадратным корнем называетсятакое число, которое ≥0
во-первых , во
вторых b2=a
2. Когда арифметический квадратный корень имеет
при a≥0
смысл?
3. Чему равен ( a )2 a
При всех ли значениях a верно равенство? при a≥0
4. Сколько корней может иметь уравнение x2=a в
зависимости от a?
1)При а>0
2) При а=0
2 корня
1 корень
X1=- а
X=0
X2=
à
3) При а<0
Корней нет
2.
36 ;100 ;
4;
1
;
9
49 ;
25
;
4
1
9;
3
0,1 100 .
3. Квадратный корень из произведения и дроби
4. Теоремы о свойствах квадратного корня:
ТЕОРЕМЫО СВОЙСТВАХ КВАДРАТНОГО КОРНЯ:
Теорема о квадратном
корне из произведения:
Корень из произведения
неотрицательных
множителей равен
произведению корней из
этих множителей.
Если
и b
, то
Теорема о квадратном
корне из дроби:
Корень из дроби, числитель
которой неотрицателен, а
знаменатель положителен,
равен корню из числителя,
делённому на корень из
знаменателя.
Если
и b >0 , то
5.
ав
а
в
а в а в
x
6. Задание 1. Вычислить:
а ) 49 0,36b) 12 3
36 6
2
c)
18
2
1 1
18
9 3
d ) 25 24
2
7 0,6 4,2
2
(25 24) (25 24)
1 49 7
7.
а ) 64 0,258 0,5 4
б) 2 8
16 4
3
в)
75
3
1 1
75
25 5
г ) 13 12
2
2
(13 12) (13 12)
1 25 5
8. Задание 2. Решите уравнения:
а) х1 2;х2 2;
а) х 4
б )корней нет;
б ) y 16
в )а1 8;
2
2
в ) а 7 71
2
а2 8.
9. Найти значение корня:
à ) 81 900;1
â) 12 ;
4
á ) 0,36 49;
9
ã) 10 .
16
10. Найдите значение корня:
á ) 0, 09 16 0, 04;à) 0, 04 81 25;
7 4
â) 1 ;
9 25
121 1
ã)
2 .
144 4
11.
а ) х 252
б )к 3 84
2
в)а 5 0
2
а ) х1 5;
х2 5;
б ) к1 9;
к 2 9
в ) корней нет.






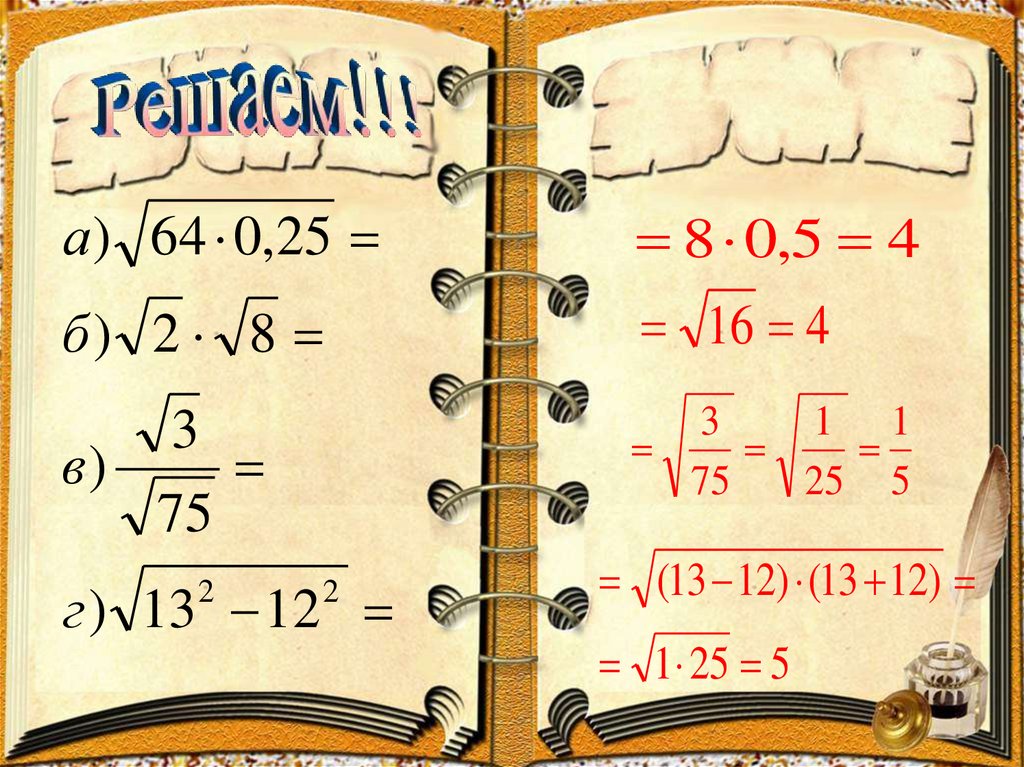



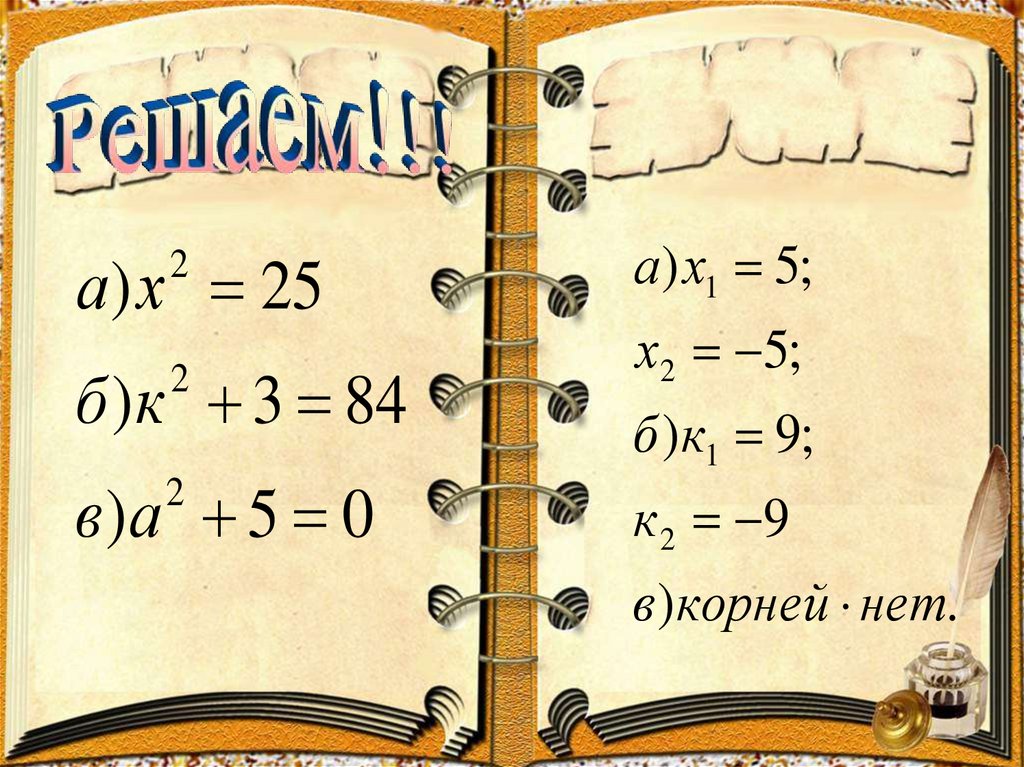

 Математика
Математика








