Подобие треугольников. Первый признак подобия

1. Blue light

Подобие треугольников.
Первый признак подобия

2. Изобразим:

• а) две неравные окружности;
• б) два неравных квадрата;
• в) два неравных равнобедренных
прямоугольных треугольника;
• г) два неравных равносторонних
треугольника.
Чем отличаются фигуры в каждой
представленной паре? Что у них
общего? Почему они не равны?

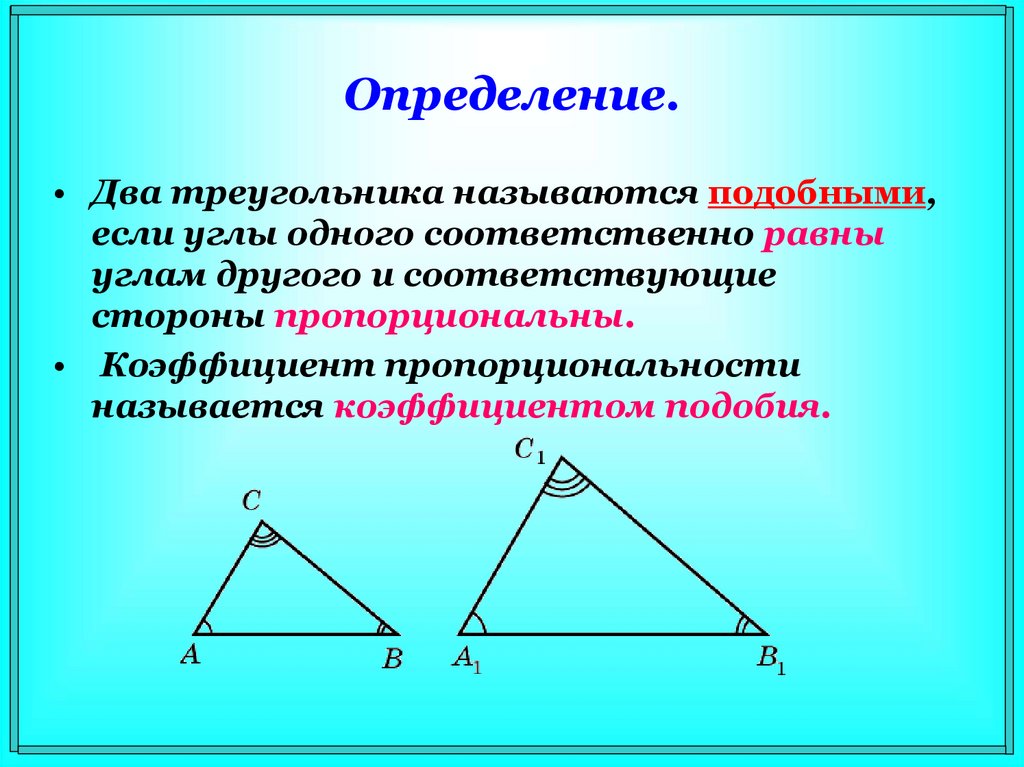
3. Определение.

• Два треугольника называются подобными,
если углы одного соответственно равны
углам другого и соответствующие
стороны пропорциональны.
• Коэффициент пропорциональности
называется коэффициентом подобия.

4. Что значит, что Δ АВС подобен треугольнику Δ A1В1С1?

Углы равны
A= A1
B= B1
Стороны пропорциональны
AB
A 1 B1
=
BC
B1 C1
=
AC
A1 C1
=
k
C= C1
Для своих изображенных пар фигур определите
их коэффициент подобия.

5.

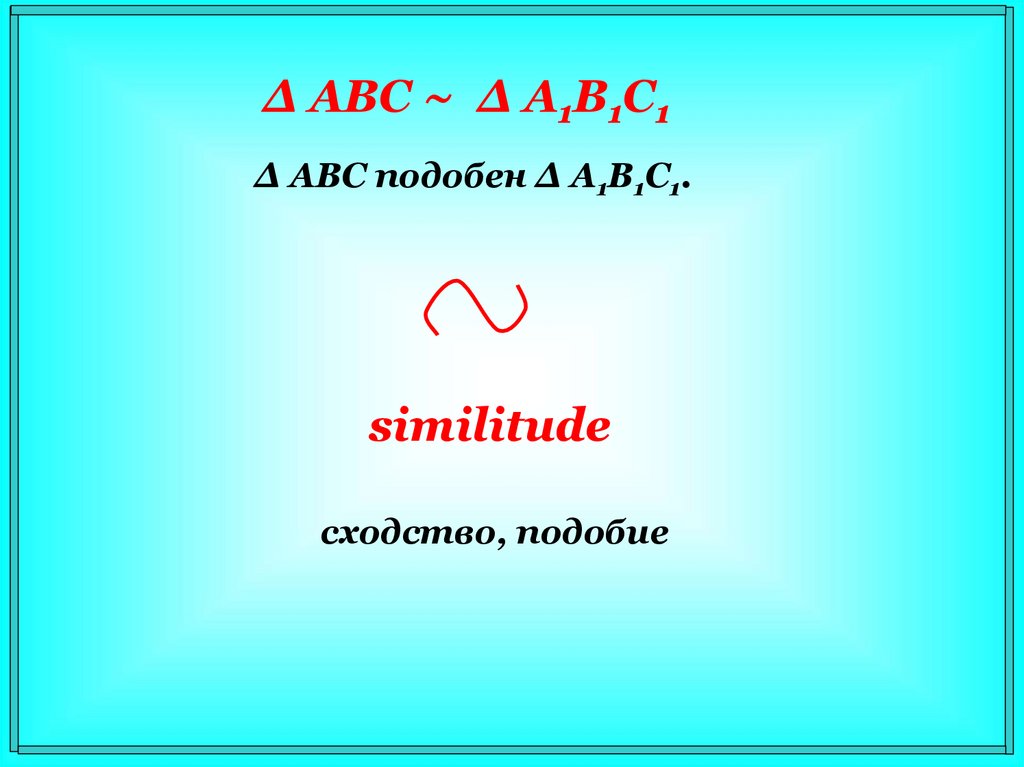
Δ АВС ~ Δ A1В1С1
Δ АВС подобен Δ A1В1С1.
similitude
сходство, подобие

6. Δ MNK ~ Δ EFD

MN
ΔM
MNK
NK
K ~ Δ EFD
E
EF
FD
D
• Укажите пропорциональные стороны
=
=

7.

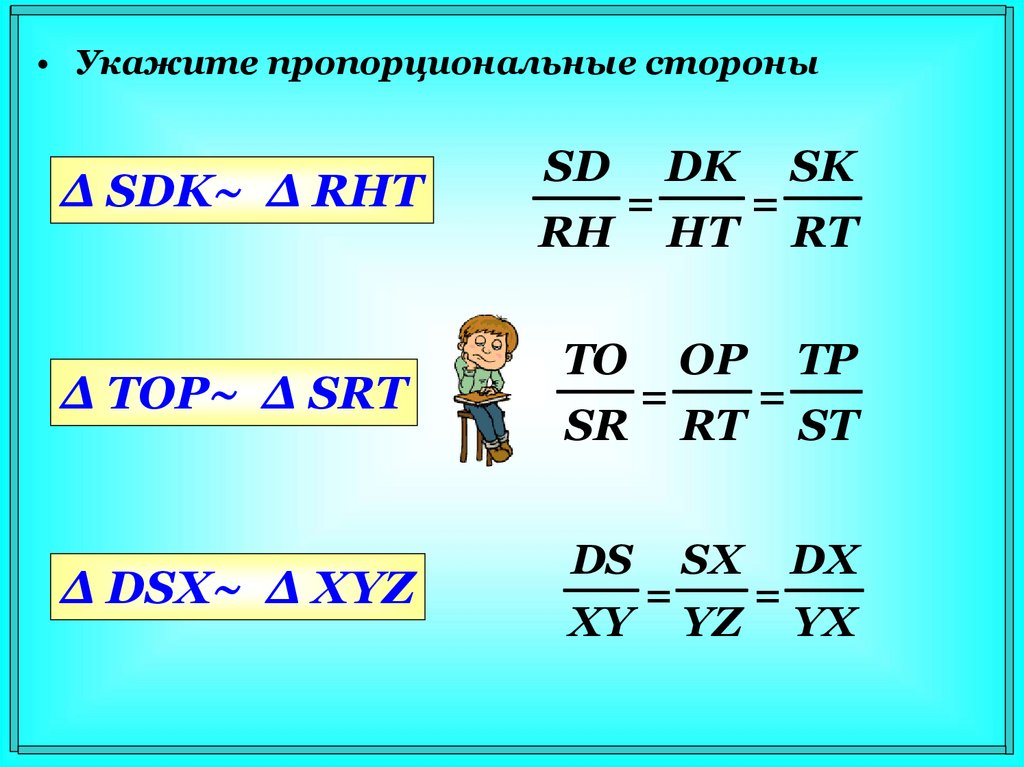
• Укажите пропорциональные стороны
Δ SDK~ Δ RHT
Δ TOP~ Δ SRT
Δ DSX~ Δ XYZ
SD
RH
=
TO
SR
DS
XY
DK
HT
=
=
OP
RT
SX
YZ
=
=
=
SK
RT
TP
ST
DX
YX

8.

Стороны треугольника равны 5 см, 8 см и 10 см.
Найдите стороны подобного ему треугольника,
если коэффициент подобия равен: а) 0,5; б) 2.
5
5
x
=
8
y
=
10
z
=0,5
x
8
y
=0,5
=0,5
10
а) 10 см, 16 см и 20 см.
б) 2,5 см, 4 см и 5 см;
z
=0,5

9.

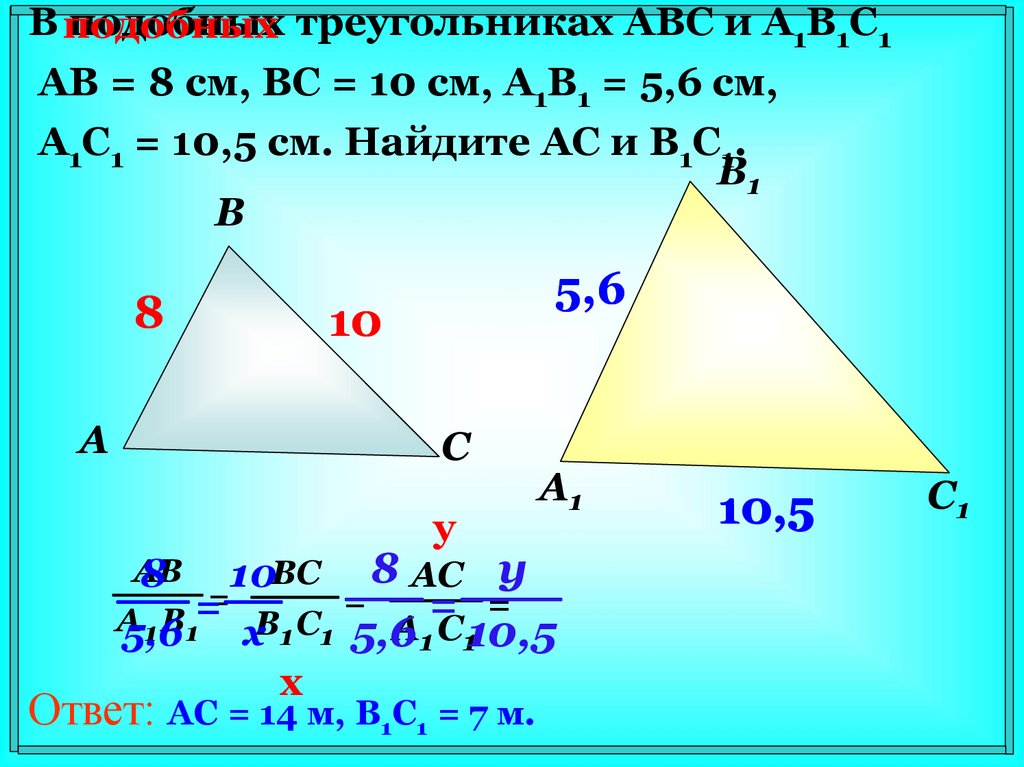
В подобных
подобных треугольниках АВС и А1В1С1
АВ = 8 см, ВС = 10 см, А1В1 = 5,6 см,
А1С1 = 10,5 см. Найдите АС и В1С1.
В1
В
8
5,6
10
А
С
y
А1
8 AC y
= =
== B C =
A
B
A1 C110,5
1 1
5,6
x 1 1 5,6
AB
8
10BC
x
Ответ: AC = 14 м, B1C1 = 7 м.
10,5
С1

10. Физкультминутка:

•– Пройдите
глазами по знаку подобия.
Физкультминутка:
– Закройте глаза.
•– Расслабьте
Долго тянется
уроклба.
мышцы
Много вы переведите
решали
– Медленно
глазные яблоки
Не поможет
звонок,
в крайнее
левоетут
положение.
– Почувствуйте
напряжение глазных мышц.
Раз глаза устали.
– Зафиксируйте
Занимаемся всеположение
сразу
– Теперь медленно с напряжением
Повторим четыре раза.
переведите глаза вправо.
– Повторите четыре раза.
– Откройте глаза.
– Пройдите глазами по знаку подобия.

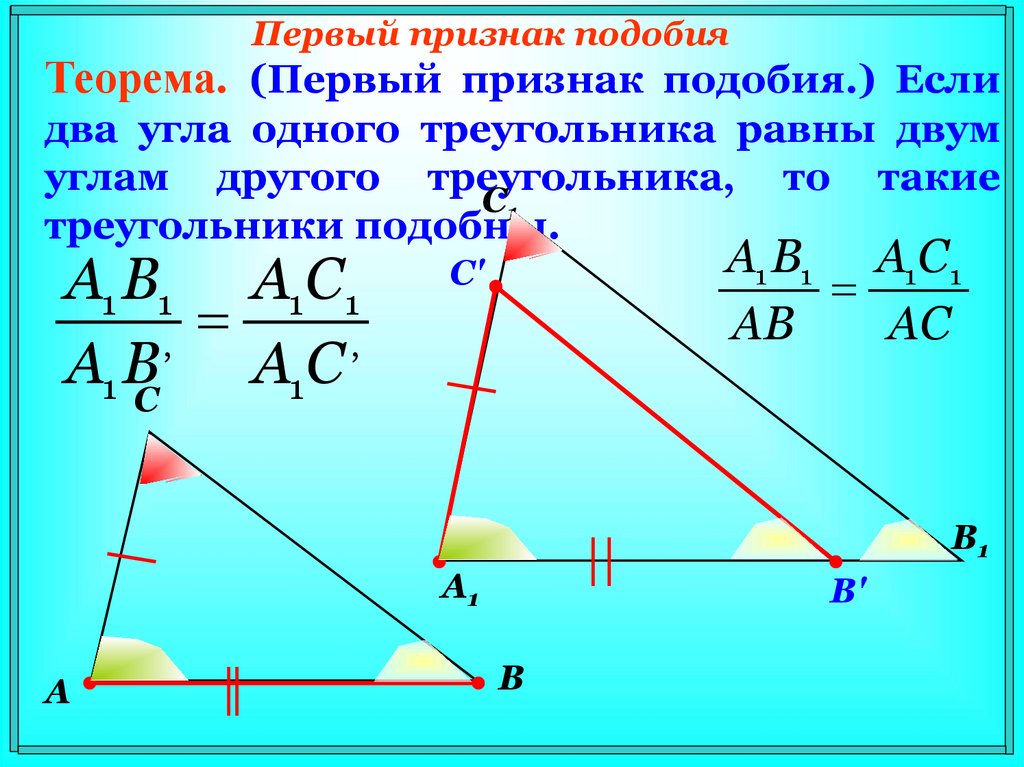
11. Первый признак подобия

Теорема. (Первый признак подобия.) Если
два угла одного треугольника равны двум
углам другого треугольника, то такие
С1
треугольники подобны.
A1 B1 A1C 1
,
,
A1 BС
A1C
A1 B1 A1C 1
AB
AC
C'
В1
А1
А
В'
В

12. Теорема. (Первый признак подобия треугольников.) Если два угла одного треугольника равны двум углам другого треугольника, то

такие треугольники
подобны.
Дано:Δ АВС и Δ А1В1С1
<A=<A1, <B=<B1.
Доказать:
Δ АВС и Δ А1В1С1.

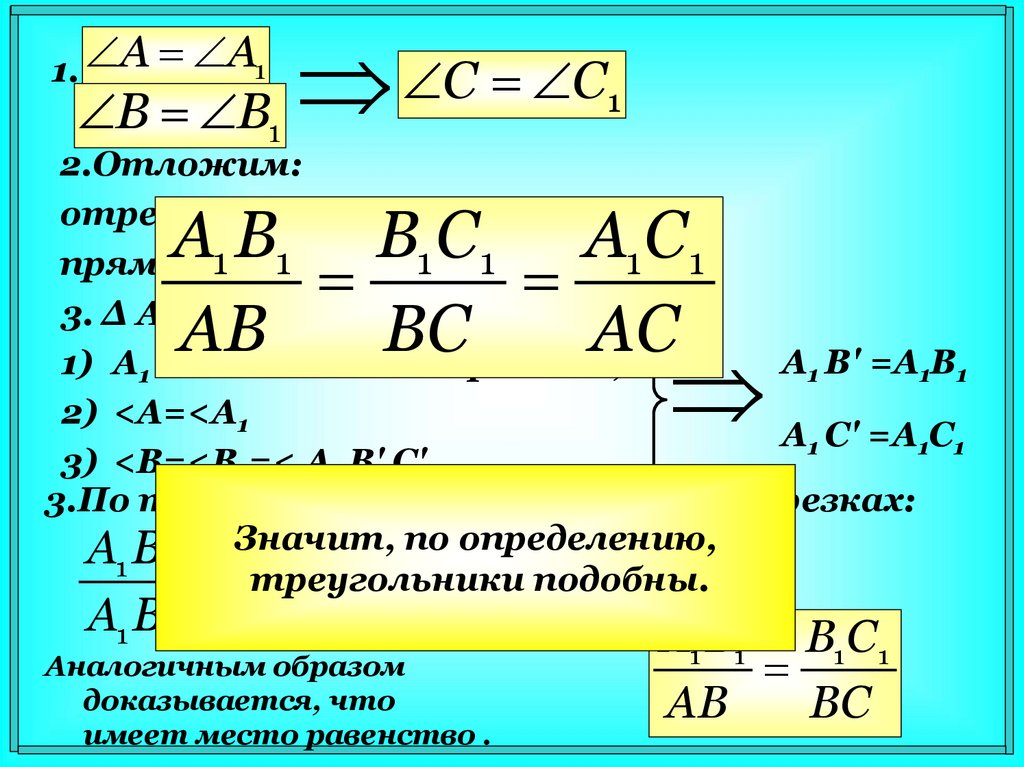
13.

C C
B B
1. A A1
1
1
2.Отложим:
отрезок АВ'= А1В1 (т. В' є AB)
1 1
прямую1В'С'1 || ВС 1 1
3. Δ АB'C' = Δ А1В1С1(по УСУ )
А1 В' =A1B1
1) А1 В' =AB – по построению,
2) <А=<A1
А1 C' =A1C1
3) <B=<B1=< А1 В' C'
3.По теореме о пропорциональных отрезках:
определению,
A1 B1 Значит,
A1C 1 Aпо
B
A1C 1
1
1
треугольники
подобны.
AB BC
AC
AB
BC
AC
A1 B ,
A1C ,
AB
Аналогичным образом
доказывается, что
имеет место равенство .
AC
A1 B1 B1C 1
AB
BC

14.

Подобны ли прямоугольные треугольники,
если у одного из них есть угол 40о, а у
другого 50о?
Два треугольника подобны. Два угла
одного треугольника равны 55о и 80о.
Найдите наименьший угол второго
треугольника.

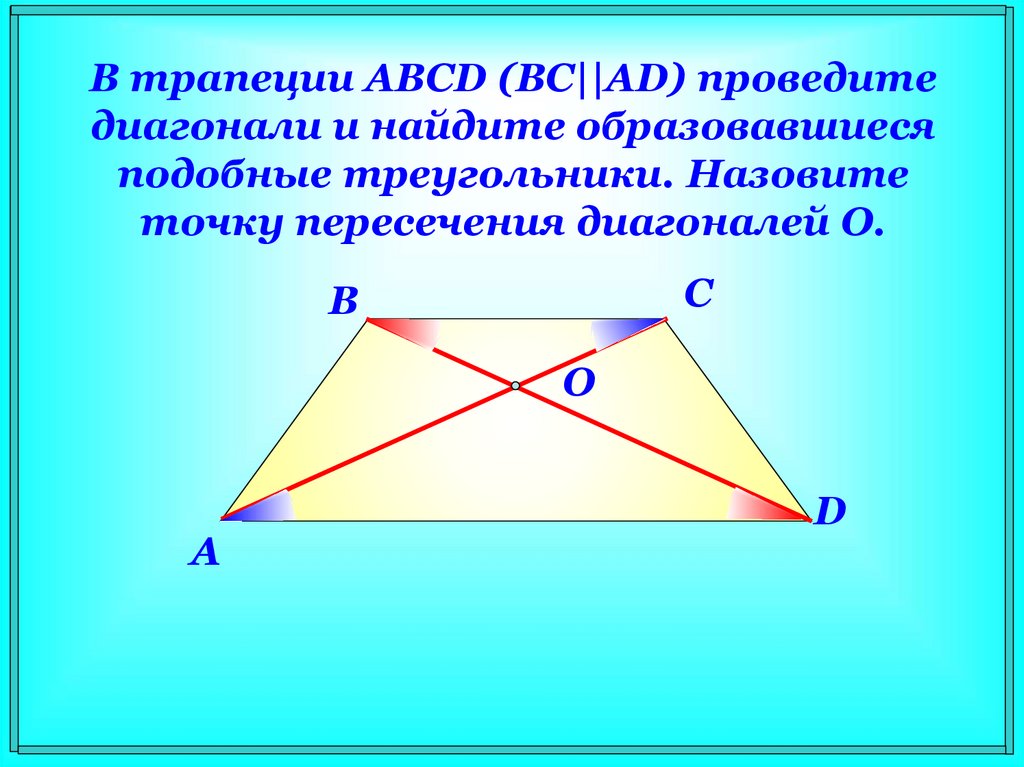
15. В трапеции ABCD (BC||AD) проведите диагонали и найдите образовавшиеся подобные треугольники. Назовите точку пересечения

диагоналей O.
C
B
O
A
D