Динамика вращательного движения твердого тела

1.

Динамика вращательного движения тв. тела
Задача динамики – нахождение угловых ускорений, сообщаемых
известными силами.
Вращательным движением твердого тела вокруг
неподвижной оси вращения называют такое
движение, при котором все точки тела движутся
по окружностям, центры которых лежат на
прямой , называемой осью вращения.
При вращательном движении точек тел,
находящихся на разном расстоянии от оси
вращения, они за одно и то же время
совершают разные перемещения и в один и
тот же момент времени имеют разные
скорости и ускорения.
company name
Для описания вращательного движения вводятся
следующие динамические параметры:
момент инерции
I
момент силы
момент импульса
M
L

2.

Динамика вращательного движения тв. тела
Момент инерции тела
Скалярная величина, характеризующая распределение масс в теле
и являющаяся мерой инертности тела при непоступательном
движении.
Момент инерции материальной точки относительно оси:
company name
I mr
2
2
I
кг
м

3.

Динамика вращательного движения тв. тела
Момент инерции системы материальных точек относительно
неподвижной оси
Момент инерции – величина аддитивная. Момент инерции с.м.т.
равен сумме произведений масс материальных точек на квадраты
их расстояний до оси вращения:
n
n
i 1
i 1
company name
I Ii
2
mi r i
Тело может двигаться, может покоиться.
К примеру, момент инерции колеса можно
посчитать даже если оно не вращается:
I mr 2

4.

Динамика вращательного движения тв. тела
Момент инерции тела относительно неподвижной оси
Момент инерции тела находится
интегрированием. Представляем тело
как систему материальных точек с
массами dm
I r dm r dV
2
company name
Если
const
dm dV
- плотность тела
2
V
V
, то
I r 2 dV
V

5.

Динамика вращательного движения тв. тела
Момент инерции тела относительно оси вращения
Момент инерции тела зависит от:
1)
2)
3)
4)
массы тела;
его формы и размеров;
распределения плотности по объему;
расположения оси вращения.
company name
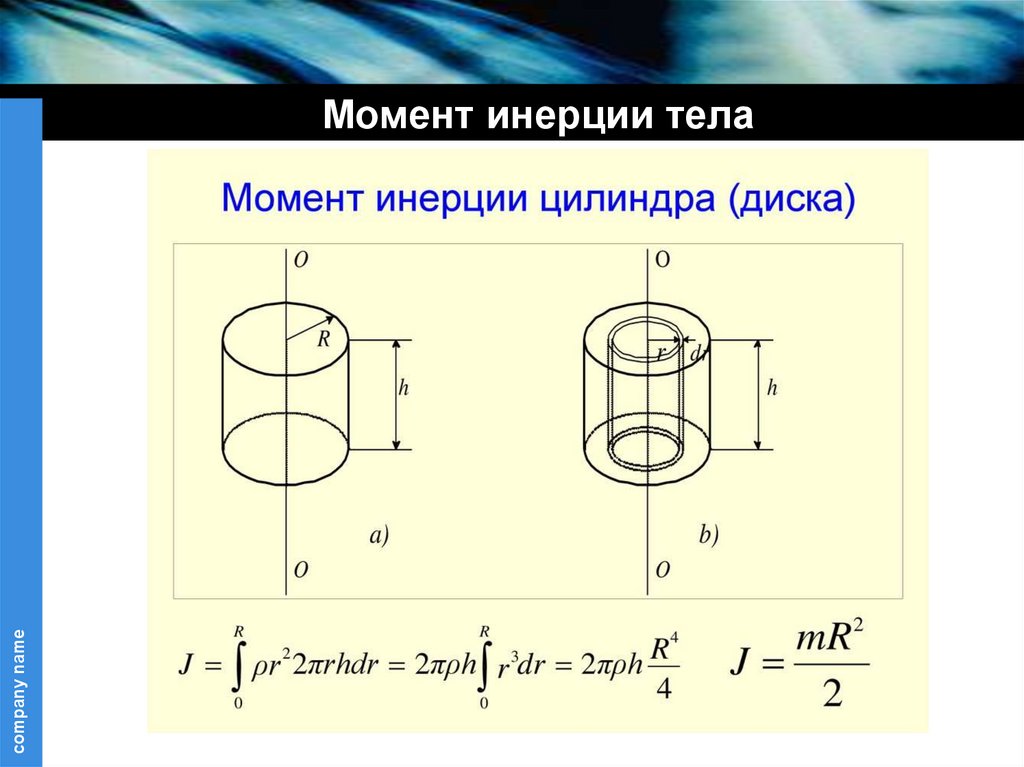
Моменты инерции
различных тел

6.

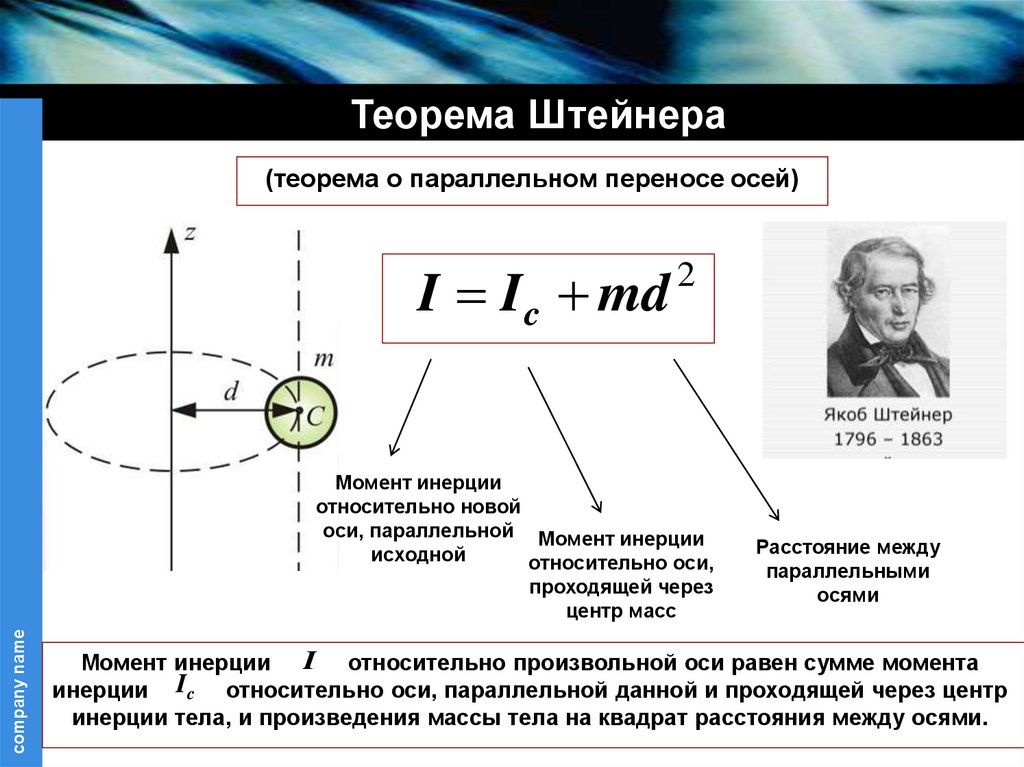
Теорема Штейнера
(теорема о параллельном переносе осей)
I I c md
2
company name
Момент инерции
относительно новой
оси, параллельной Момент инерции
исходной
относительно оси,
проходящей через
центр масс
Расстояние между
параллельными
осями
Момент инерции I относительно произвольной оси равен сумме момента
инерции Ic относительно оси, параллельной данной и проходящей через центр
инерции тела, и произведения массы тела на квадрат расстояния между осями.

7.

Момент инерции тела
Момент инерции однородного стержня относительно оси,
проходящей через его центр инерции и через его край
Момент инерции относительно оси zc , проходящей
перпендикулярно стержню через его центр:
1) выделим элемент длины стержня длиной dr
на расстоянии r оси вращения,
2) возьмем небольшой отрезок длины этого
стержня
dm
- линейная плотность стержня
dl
company name
Решаем задачу интегрированием:
l 2
3 l 2
l
2
2
I l dl l dl
3
V
l 2
l 2
l 3 l 3 l 3 ml 2
; l m
3 8 8 12
12

8.

Момент инерции тела
Момент инерции однородного стержня относительно оси
проходящей через конец стержня
z
,
Воспользуемся теоремой Штейнера:
2
company name
ml 2 ml 2 ml 2
l
I z Ic m
12
4
3
2
ml 2
Iz
3

9.

company name
Момент инерции тела

10.

Динамика вращательного движения тв. тела
Уравнение моментов
Рассмотрим механическую систему, состоящую из n тел, масса и
скорость которых равны m1, m2, ... mn ; V 1, V 2, ... V n
внутренние силы,
действующие на 1-ое
тело со стороны 2-го,
3-го и т.д.
внешние
силы,
i действующие на 1-ое,
2-ое тело и т.д.
F 12 , F 13 , ... F ik -
F 1, F 2, ... F
company name
ri
- радиус-вектор i-ой точки
n
d
mi Vi F ik F i
dt
k 1
- уравнение динамики движения
i-ой точки

11.

Динамика вращательного движения тв. тела
n
d
mi Vi F ik F i
dt
k 1
ri
умножаем векторно
на радиус-вектор
n
d
ri dt mi Vi ri F ik ri F i
k 1
company name
d
ri dt mi Vi - ?
Выполним
преобразования:
d ri
d
d
ri mi Vi
mi Vi ri
mi Vi
dt
dt
dt

12.

Динамика вращательного движения тв. тела
a b c
c a b sin a , b
d ri
mi Vi Vi mi Vi 0
dt
следовательно
company name
Обозначим:
d
d
r
m
V
=
r
m
V
i
i
i
i
i
i
dt
dt
Li ri mi Vi
момент импульса i-ой материальной
точки
r V

13.

Динамика вращательного движения тв. тела
Моментом импульса (количества движения) материальной точки
относительно неподвижной точки О называется физическая величина,
определяемая векторным произведением:
L r p r mV
кг м 2
с
Направление вектора L совпадает с
направлением
поступательного
движения правого винта при его
вращении от r к p .
Модуль момента импульса равен
company name
L r p sin p l
l r sin
, где
- плечо вектора
относительно т.О
p

14.

Динамика вращательного движения тв. тела
Моментом импульса относительно неподвижной оси называется
скалярная величина, равная проекции на эту ось вектора момента
импульса, определенного относительно произвольной точки данной оси.
Lz r mV
z
Это скалярная величина, равная
по модулю:
Lz L cos
company name
Она не зависит от выбора т.O на оси OZ и
характеризует
способность
импульса
изменять вращение тела вокруг этой оси.
Момент
импульса
твердого
тела
относительно оси есть сумма моментов
импульса отдельных частиц:
n
n
i 1
i 1
Lz Li miVi ri

15.

Динамика вращательного движения тв. тела
n
n
i 1
i 1
Lz miVi ri
Vi ri
n
2
m
r
ii
mi ri2
i 1
n
I mi ri2
Lz I z
i 1
Момент импульса твердого тела относительно оси равен произведению
момента инерции тела относительно той же оси на угловую скорость.
company name
Определения эквивалентны:
L r p
L I

16.

Динамика вращательного движения тв. тела
Моментом силы относительно неподвижной точки О называется
векторная величина, определяемая векторным произведением радиусвектора, проведенного из точки О в точку приложения силы, на силу.
M r F
Н м
т. А – точка приложения силы
т. О – начало (центр)
Модуль момента силы:
M r F sin F l
l r sin
- плечо силы
company name
(кратчайшее расстояние между линией
действия силы и точкой О)
Направление момента силы совпадает с
осью вращения и определяется по
правилу правого винта (буравчика).

17.

Динамика вращательного движения тв. тела
Моментом силы относительно неподвижной оси z называется скалярная
величина, равная проекции на эту ось вектора момента силы,
определенного относительно произвольной точки данной оси.
M z r F
z
Н м
Mz M cos rF sin cos
company name
- угол между
- угол между
F
r
и
M
и осью z
Вектор M перпендикулярен плоскости, в
которой лежат векторы r и F .

18.

Динамика вращательного движения тв. тела
Работа и кинетическая энергия при вращательном движении
твердого тела
dS rd
F F sin
- проекция вектора силы
на направление пути
Работа силы
равна произведению
проекции
силы
на
направление
смещения F и смещения dS :
company name
dA F dS F sin rd
Fr sin Mz
dA Md
Работа силы при вращении тела вокруг неподвижной оси равна
произведению момента действующей силы на угол поворота.

19.

Динамика вращательного движения тв. тела
dA Md
A M d M
0
Кинетическая энергия вращательного движения твердого тела
относительно неподвижной оси
Кинетическая энергия - величина аддитивная
miVi2 m1V12 m2V22
mnVn2
..
2
2
2
2
i 1
n
Eкин
company name
Т.к. тело абсолютно твердое, угловые скорости всех его точек
одинаковы, а линейные скорости разные
Vn
V1 V2
..
r1 r2
rn
mi 2 ri2 2 n
2
2
2
2
2
m
r
m
r
m
r
...
m
r
i i
11
2 2
n n
2
2
2
i 1
i 1
n
Eкин
V1 r1 , V2 r2 , Vn rn

20.

Динамика вращательного движения тв. тела
I m1r12 m2 r22 .. mn rn2
Кинетическая энергия вращающегося тела:
Eкин
I 2
2
Кинетическая энергия тела, катящегося без
скольжения:
mV 2 I 2
Eкин
2
2
Основное уравнение вращательного движения твердого тела
вокруг неподвижной оси
company name
Работа внешних сил при вращении тела идет на увеличение его
кинетической энергии:
dA dEкин Eкинкон Eкиннач
I 2
Md d
I d
2
I 2кон I 2нач
2
2
dt

21.

Динамика вращательного движения тв. тела
d
d
M
I ;
dt
dt
d
;
dt
M I
M I
d
dt
или
M
I
Основное уравнение динамики вращательного движения или
второй закон Ньютона для вращательного движения
Между
кинематическими
и
динамическими
параметрами
поступательного и вращательного движения существует аналогия:
a
company name
m I
Для мат. точки:
V
L r mV
p L
F M
, продифференцируем это уравнение по
времени:
d L dr
dp
p r
V p r F
dt
dt
dt

22.

Динамика вращательного движения тв. тела
company name
M
I
Основное уравнение динамики вращательного движения
или второй закон Ньютона для вращательного движения
Пример:
ФИГУРНОЕ КАТАНИЕ

23.

Динамика вращательного движения тв. тела
d L dr
dp
p r
V p r F
dt
dt
dt
M
V - скорость мат. точки
равно нулю
F - сила, действующая на
- момент силы
мат. точку
company name
dL
M
dt
- уравнение моментов
Скорость изменения момента импульса тела
относительно неподвижной оси вращения равна
результирующему моменту относительно этой оси
всех внешних сил, действующих на тело.
Если система замкнута, т.е. на нее не
dL
действуют внешние силы, то момент
0
M 0
dt
внешних сил равен нулю
L const , если
F внеш 0
момент импульса замкнутой с.м.т.
остается постоянным

24.

Динамика вращательного движения тв. тела
dL
M
dt
- уравнение моментов
Дополнение первое:
Система незамкнута, т.е. на нее
действуют внешние силы, но
суммарный момент внешних сил
равен нулю
Mi 0
L const , если
M внеш M i 0
company name
Дополнение второе:
Система незамкнута, т.е. на нее
действуют внешние силы и
суммарный момент внешних сил
не равен нулю. Но проекция
момента внешних сил
относительно некоторой оси
равна нулю.
Mi 0
Lx const
внеш
Mx
, если
M ix 0

25.

Динамика вращательного движения тв. тела
company name
Замечание:
Момент импульса системы изменяется только под
действием внешних сил !!!
Внутренние силы не могут изменить момент импульса
системы материальных точек !!!