Динамика вращательного движения твердого тела

1. Динамика вращательного движения твердого тела

Лекция по физике

2.

Твердое тело – это система материальных точек, расстояния
между которыми не меняются в процессе движения.
При вращательном движении твердого тела все его точки
движутся по окружностям, центры которых лежат на оси вращения.
Рассмотрим основные законы вращательного движения твердого
тела.
1. Момент инерции
Момент инерции материальной точки относительно оси
вращения равен произведению массы точки на квадрат расстояния от
нее до оси вращения
C
J = mR
2
(1.1)
Момент инерции точки зависит
только от ее кратчайшего расстояния до оси
вращения.
.
R
r
O
m

3.

Для системы материальных точек момент инерции равен
сумме моментов инерции отдельных точек
J = J i = mi R
2
i
i
i
Если масса распределена непрерывно с плотностью (r ) , то
тело можно разбить на малые объемы ΔVi с массами Δmi = ρi ΔVi.
Эти объемы можно рассматривать как материальные точки.
Суммируя их моменты инерции, получим момент инерции всего тела
J = Δmi R = ρi ΔVi R
2
i
i
2
i
i
В пределе ΔVi 0 сумма переходит в интеграл по объему тела
J = R dm = R ρdV
2
2
(1.2)
Момент инерции твердого тела зависит от распределения в нем
массы, расстояния и ориентации оси относительно тела.

4.

В качестве примера найдем момент инерции однородного диска
относительно оси, перпендикулярной к его плоскости и проходящей
через его центр.
Пусть D - толщина диска, R0 – его радиус. Поскольку диск
однородный ( ρ = const ), то
J = R ρdV = ρ R dV
2
2
Разобьем диск на тонкие
кольцевые слои толщиной dR
и радиусами R.
Объем каждого слоя равен
dV = D 2πRdR

5.

Момент инерции диска равен сумме моментов инерции всех
кольцевых слоев, поэтому он равен интегралу
R0
π
4
J = D 2π ρ R dR = D ρ R0
2
0
3
Выражая массу диска через плотность
m = πR D ρ
2
0
получаем момент инерции однородного диска или цилиндра
1
2
J = m R0
2
(1.3а)

6.

Аналогичные расчеты дают моменты инерции :
1) стержня длиной
стержня)
l
(вокруг оси, проходящей через середину
1
2
J=
m l
12
(1.3b)
2) шара с радиусом R0 (вокруг оси, проходящей через центр шара)
2
2
J = m R0
5
3) полого тонкостенного цилиндра с радиусом
симметрии цилиндра)
J = m R
2
0
(1.3c)
R0 (вокруг оси
(1.3d)

7.

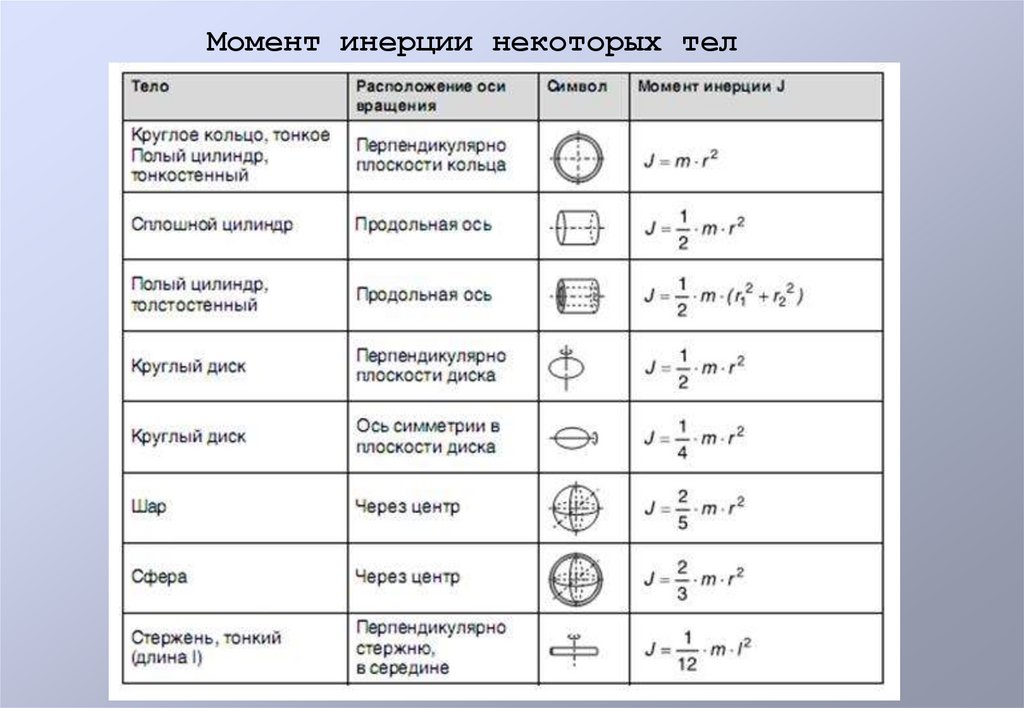
Момент инерции некоторых тел

8.

2. Теорема Штейнера
До сих пор момент инерции определялся относительно оси
симметрии, проходящей через центр масс тела. Теперь найдем
2
момент инерции тела относительно
оси.
F = - m произвольной
R
Пусть ось С проходит через центр
C'
C
масс тела О . Разобьем тело на
малые объемы с массами Δmi и
радиус-векторами Ri ,
перпендикулярными к оси С.
m
i
an
Момент инерции относительно оси
Ri
Ri '
С равен
Jc =
Δmi Ri2
.
a
.
i
O
R
Пусть некоторая другая ось С ′
параллельна оси С и отстоит от нее
'
на расстояние а. Введем векторы Ri
и a , перпендикулярные двум осям
'
i
R = a + Ri

9.

Квадрат расстояния элементарной массы Δmi до оси С ′ равен
(R'i )2 (a Ri ) (a Ri ) a 2 + 2(a Ri ) Ri 2
Поэтому момент инерции тела относительно оси С ′ равен
J ' = mi (R'i ) 2 a 2 mi 2a mi Ri + mi Ri2
i
Здесь
i
i
i
Δm = m - масса тела. Последнее слагаемое есть момент
i
инерции относительно оси С, т.е. Jс . Сумма Δmi Ri
равна
произведению массы тела на вектор RЦм , направленный от оси С
к центру масс. Поскольку центр масс лежит на оси С, то RЦм = 0 ,
поэтому среднее слагаемое равно нулю, в результате получаем
теорема Штейнера
'
2
J = ma + J c
(2.1)
Момент инерции относительно произвольной оси равен сумме
момента инерции относительно оси, параллельной данной и
проходящей через центр масс тела, и произведения массы тела
на квадрат расстояния между осями.

10.

3 . Кинетическая энергия вращающегося тела
Кинетическая энергия вращающегося тела равна сумме
кинетических энергий его частей
m
ω
Jω
2
Т =
=
mi Ri =
2
2 i
2
i
2
i i
где
2
2
(3.1)
- угловая скорость вращения тела вокруг оси.
Сравнивая формулу (3.1) с формулой для кинетической
энергии поступательного движения
mυ2/2 видим, что
при вращательном движении мерой инерции тела
выступает момент инерции.

11.

Если тело участвует в составном движении, то его
кинетическая энергия складывается из энергии поступательного
движения и энергии вращения.
Например, у цилиндра, катящегося без скольжения по
плоскости, полная кинетическая энергия равна
m
J cω
Т=
+
2
2
2
c
2
(3.2)
m – масса цилиндра, υc – величина скорости его центра
масс, Jc – момент инерции цилиндра относительно оси,
где
проходящей через центр масс.

12.

4 . Момент силы
Пусть точка О – неподвижная точка в твердом теле, и к
некоторой точке тела А с радиус-вектором r , проведенным из О,
приложена сила F . Тогда векторное произведение
M = [r F ]
(4.1)
называется моментом силы F относительно неподвижной точки О.
M
Момент силы является псевдовектором,
его
направление
совпадает
с
направлением
поступательного
движения правого винта при его
вращении от r к F . Модуль момента
силы равен
O
r
l
A
F
M = r F sinα = F l
где
l = r sinα -
плечо силы.

13.

Момент силы характеризует способность силы вращать тело
вокруг точки, относительно которой она берется.
Пусть через точку О проходит некоторая ось z. Тогда проекция
вектора M на эту ось называется моментом силы относительно оси
M z = [r F ]z
z
M
Mz
F
(4.2)
Mz – скаляр, он не зависит от
положения точки О на оси z,
его величина равна
b
r
O
l
A
M z = M cosb
где b
- угол между вектором M
и осью
z.

14.

5 . Работа силы при вращательном движении твердого тела.
Основное уравнение динамики вращательного движения.
Рассмотрим тело, вращающееся вокруг оси z под действием силы F ,
приложенной к точке тела А. Пусть эта сила лежит в плоскости,
перпендикулярной оси вращения, тогда угол b 0 и вектор момента
силы M совпадает с осью z. Найдем работу силы при повороте тела
на малый угол dj. На рисунке ось z выходит из листа в точке О.
A'
O
r'
d j dr
r
A
F
Из-за малости угла dj можно считать,
что вектор перемещения dr точки А
перпендикулярен исходному вектору r
r dr
Так как тело абсолютно твердое, то
элементарная работа силы dA равна
работе, затраченной на поворот всего
тела, что эквивалентно работе по
перемещению точки А на вектор dr .

15.

Вектор перемещения
dr можно записать в виде
dr
dr = dr e ; e =
; dr = r dj ; dr = e r dj
dr
e - единичный вектор, направленный вдоль вектора перемещения.
Подставляя в формулу для элементарной работы, получаем
dA = (F dr) = (F e) dj r
Угол между вектором силы Fи вектором e равен (90°- ), поэтому
(F e) = F sin
dA = F sin r dj M z dj
При повороте на конечный угол работа силы F равна интегралу
j
A = M z dj
j
(4.3)

16.

С другой стороны, элементарная работа силы по вращению
тела идет на увеличение его кинетической энергии
J z ω2
dA = dT = d(
) = J z ωdω
2
Следовательно
dj
dω
M z dj = J z ωdω
Mz
= J zω
M z ω = J z ωε
dt
dt
e
где
– угловое ускорение.
В результате получаем основное уравнение динамики вращательного
движения твердого тела относительно неподвижной оси
Mz = J z ε
(4.4)
Это уравнение играет во вращательном движении тела такую
же роль, какую 2 -й закон Ньютона играет в поступательном
движении тела.

17.

5. Момент импульса
Моментом импульса материальной точки А относительно
неподвижной точки О называется псевдовектор, равный
L = [r p] [r m ] (5.1)
L
z
где - радиус-вектор точки А .
Направление псевдовектора L
совпадает с направлением
поступательного движения правого
винта при его вращении от r к p .
Модуль момента импульса равен
r
b
R
O
b
l
P
r
A
L = r p sinα = p l
где l = r sinα - плечо импульса

18.

Моментом
импульса
материальной
точки
относительно неподвижной оси z называется величина,
равная проекции вектора момента импульса на эту ось
Lz = [r p]z L cosβ
(5.2)
Для твердого тела момент импульса относительно
неподвижной точки равен сумме моментов элементарных объемов,
выступающих в роли материальных точек
L = Li = [ri pi ]
i
i

19.

Поэтому
момент
неподвижной оси
тела
z
импульса
твердого
тела
относительно
равен сумме моментов элементарных объемов
Lz = Liz = [ri pi ]z Li cosb i
i
i
i
Пусть тело вращается вокруг неподвижной оси z с угловой
скоростью
. Каждая точка тела движется по окружности
постоянного радиуса Ri со скоростью i , перпендикулярной этому
радиусу и радиус-вектору точки ri , поэтому угол между
i и ri прямой i = /2 .

20.

Поскольку плечо силы
i - ой точки равно Ri = ri cos b i
, то
[ri pi ]z ri pi sin i cosb i Ri pi
Lz Ri pi Ri mi i
i
i
При вращательном движении все точки тела движутся с одной
угловой скоростью
, величина которой связана с линейной
скоростью υi = ω Ri , поэтому
Lz mi Ri = J z
2
Lz J z
i
(5.3)
Момент импульса твердого тела относительно оси
равен произведению моменту инерции тела относительно
той же оси на угловую скорость.

21.

Возьмем производную по времени от последнего равенства
dLz d ( J z )
d
=
= Jz
Jz e
dt
dt
dt
Но согласно (4.4)
относительно оси z , поэтому
Mz = J z e -
есть момент силы
dLz
Mz =
dt
(5.4)
Производная по времени от момента импульса
твердого тела относительно некоторой оси равна моменту
внешних сил относительно той же оси.
Уравнение (5.4) есть другая форма уравнения динамики
вращательного движения твердого тела. Она устанавливает связь
между проекциями векторов M и L на ось вращения.

22.

Теперь найдем связь между векторами M и L .
Для этого возьмем производную по времени от формулы (5.1) для
вектора L
dL
dL
dr
dp
dt
=
i
i
dt
= [
i
i
dt
pi ] [ri
i
i
dt
]
dri
pi ] = [ i pi ] = mi [ i i ] = 0
Но [
dt
dL
dpi
= [ri
] [ri Fi ] M i M
поэтому
dt
dt
i
i
i
Уравнение динамики вращательного
движения твердого тела в векторном виде
dL
=M
dt
(5.5)
Производная по времени от момента импульса
твердого тела относительно неподвижной точки равна
моменту внешних сил относительно той же точки.