Кривые второго порядка

1.

Эллипсом называется геометрическое место всех точек
плоскости, для которых сумма расстояний до двух заданных
точек, называемых фокусами, есть величина постоянная (её
обозначают 2a), причем эта постоянная больше расстояния
между фокусами.
Каноническое уравнение
эллипса
Связь между a, b, c
r1 r2 2a
( x с ) y ( x с ) y 2а
2
2
2
2
x2 y2
1
a2 b2
b2 a2 c2 , a b
А1 а, 0 , А2 (а, 0)
Вершины эллипса
В1 (0, b), В2 (0, b)
Большая ось А1 А2
А1 А2 2a
Малая ось B1 B2
B1 B2 2b
Фокусы
F1 c, 0 , F2 (c, 0)
Фокусное расстояние F1 F2 F1 F2 2c
Эксцентриситет
с
, 0 1
a

2.

Каноническое уравнение
эллипса
x2 y2
1
a2 b2
Связь между a, b, c
а2 b2 c2 , b a
Вершины эллипса
Большая ось
Малая ось
B1B2
А1 А2
Фокусы
А1 а, 0 , А2 (а, 0)
В1 (0, b), В2 (0, b)
B1 B2 2b
А1 А2 2a
F1 0, c , F2 (0, c)
Фокусное расстояние F1 F2
F1F2 2c
Эксцентриситет
с
b

3.

Найти длины осей, координаты фокусов и эксцентриситет эллипса:
16 х 2 25 у 2 400
Решение:
16 х 2 25 у 2 400
400
400 400
х2 у2
1
25 16
a 2 25, b 2 16
2a 10
2b 8
- малая ось
2
F c, 0
с
a
a 5, b 4
- большая ось
а с b
2
x2 y2
2 1
2
a
b
2
с 2 a 2 b 2 , с 2 25 16 9, с 3
F1, 2 ( 3,0)
- координаты фокусов
3
0,6 - эксцентриситет эллипса
5

4.

Найти длины осей, координаты фокусов и эксцентриситет эллипса:
2 х 2 у 2 32
Решение:
2 х 2 у 2 32
32 32 32
2
2
x
y
2 1
2
a
b
х2 у2
1
16 32
a 2 16, b 2 32
a 4, b 4 2
2a 8
- малая ось
2b 8 2
- большая ось
b с a
F 0, c F1, 2 (0, 4)
2
2
2
с b a , с 32 16 16, с 4
2
2
2
2
- координаты фокусов
с
4
1
2
b
2
4 2
2
- эксцентриситет эллипса

5.

Пример. Составить уравнение эллипса c фокусами на оси Ох ,
если фокусное расстояние равно 10, а малая ось равна 6.
Решение.
2c 10
c 5
2b 6
b 3
а2 с2 b2
а 2 b 2 с 2 32 52 34
Итак, каноническое уравнение эллипса имеет вид
x2 y2
1
34 9

6.

Пример. Составить уравнение эллипса с фокусами на оси Оу,
2
если его большая ось равна 14 и .
3
Решение. Так как фокусы лежат на оси Оy, то 2b
2
14
c 2
.
и , откуда c b
3
3
b 3
b 7,
2
245
14
а b с 7
9
3
2
2
2
2
Итак, каноническое уравнение эллипса будет
x2
y2
1,
245 49
9
9x2 y2
1
245 49
14 ,
то есть

7.

Гиперболой называется геометрическое место всех точек
плоскости, абсолютная величина (модуль) разности расстояний от
которых до двух данных точек, называемых фокусами, есть
величина постоянная (её обозначают 2a), причем эта постоянная
меньше расстояния между
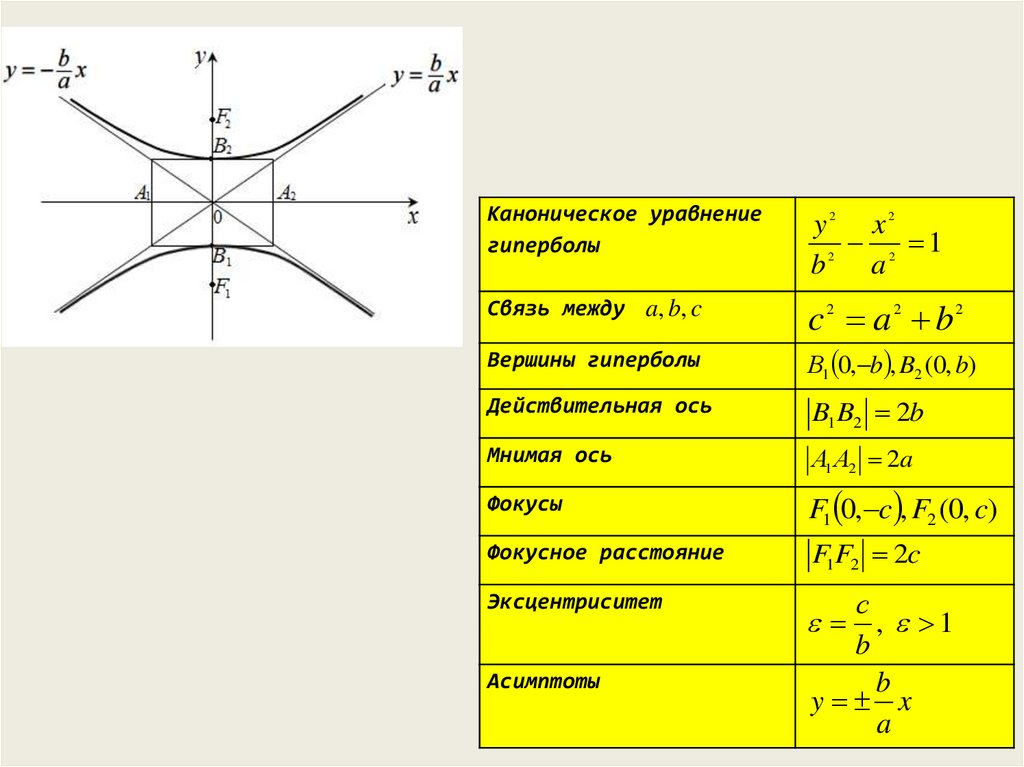
Каноническое уравнение
2
2
фокусами.
x
y
гиперболы
2 1
2
a
b
r1 r2 2a
Связь между
a, b, c
Вершины гиперболы
( x с ) 2 y 2 ( x с ) 2 y 2 2а
Действительная ось
Мнимая ось
B1B2
Фокусы
Фокусное расстояние
Эксцентриситет
Асимптоты
А1 А2
F1 F2
c2 a 2 b2
А1 а, 0 , А2 (а, 0)
А1 А2 2a
F1 F2 2c
B1 B2 2b
F1 c, 0 , F2 (c, 0)
F1F2 b2c
y x
с a
, 1
a
b
y x
a

8.

Каноническое уравнение
гиперболы
y2 x2
2 1
2
b
a
Связь между a, b, c
c2 a 2 b2
В1 0, b , B2 (0, b)
Вершины гиперболы
Действительная ось
B1 B2 2b
Мнимая ось
А1 А2 2a
Фокусы
F1 0, c , F2 (0, c)
Фокусное расстояние
F1F2 2c
Эксцентриситет
, 1
Асимптоты
b
y x
a
с
b

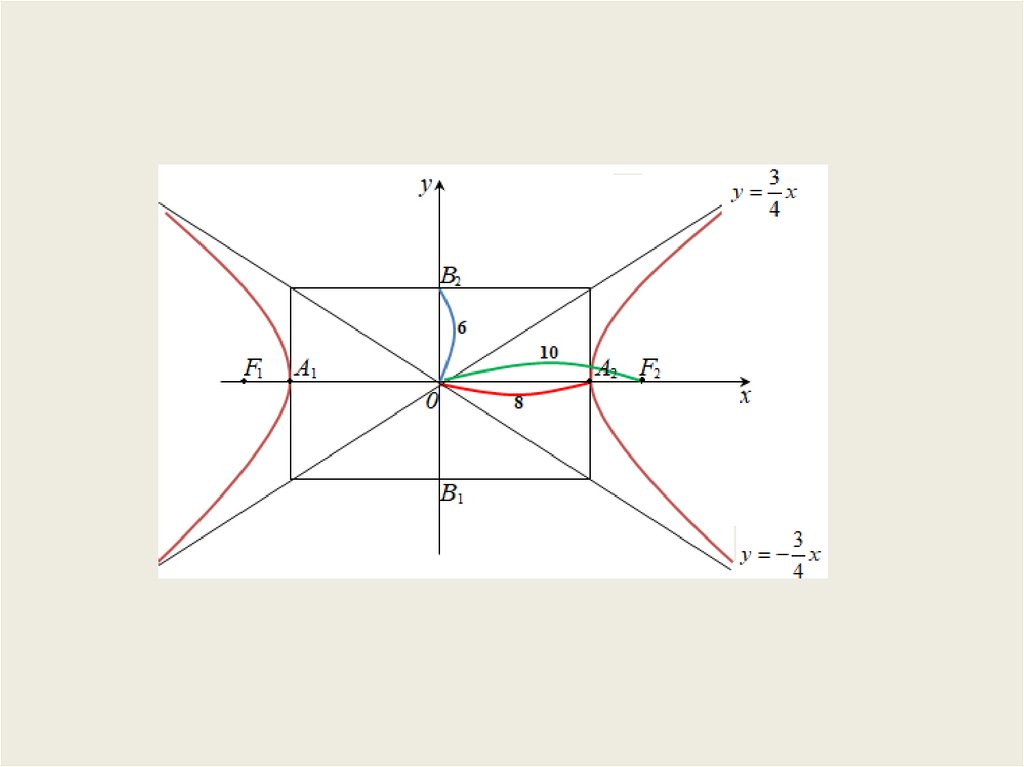
9.

Найти длины осей, координаты фокусов, эксцентриситет и
уравнения асимптот гиперболы 36 х 2 64 у 2 2304.
Решение:
x2 y2
2 1
2
a
b
36 х 2 64 у 2 2304
2304 2304 2304
х2 у2
1
64 36
a 2 64, b 2 36
2a 16
2b 12
a 8, b 6
- действительная ось
- мнимая ось
c2 a2 b2
F c, 0
с 64 36 100, с 10
2
F1, 2 ( 10,0) - координаты фокусов
с 10 1,25 - эксцентриситет гиперболы
8
a
3
у х
4

10.

11.

2.
если
Составить уравнение гиперболы с фокусами на оси Ох,
1) 2a 12, 2с 20
2) F ( 2 2 ,0), 2
1) 2a 12, 2с 20
b c a
2
2
4) 2a 16, А( 10, 3)
6) F ( 2 2 ,0), у 3 х
a 6, с 10
c2 a2 b2
2
b 2 10 2 6 2 100 36 64
2
2
x
y
1
36 64
x2 y2
2 1
2
a
b
- уравнение гиперболы
F c, 0

12.

2) F ( 2 2 ,0), 2
с 2 2
F ( 2 2 , 0)
x2 y2
2 1
2
a
b
с
c 2 2
a
2
a
2
2
2
b c a 2 2
2
2
2
x2 y2
1
2
6
c2 a2 b2
2
8 2 6
- уравнение гиперболы
F c, 0

13.

4) 2a 16, А( 10, 3)
a 8
x2 y2
2 1
2
a
b
Так как точка А принадлежит гиперболе, то ее координаты
удовлетворяют каноническому уравнению гиперболы, то есть
( 10) 2 ( 3) 2
2 1
2
8
b
9 100
100 9
1
2 1
2
b
64
64 b
36 b 2 9 64
9 64
2
b
16
36
2
2
x
y
1
64 16
- уравнение гиперболы
9 36
2
b
64

14.

F c, 0
6) F ( 2 2 ,0), у 3 х
с 2 2
b
3
a
с2 8
b 3a
b
y x
a
b 2 3a 2
c2 a2 b2
8 a 2 3a 2 4a 2 8, a 2 2
x2 y2
1
2
6
b2 3 2 6
2
- уравнение гиперболы
2
x
y
2 1
2
a
b

15.

Написать уравнение гиперболы, имеющей вершины в фокусах
эллипса, а фокусы в вершинах эллипса x y 1 .
2
25
2
9
x2 y2
2 1
2
a
b
a 2 25, b 2 9 a 5, b 3
b 2 a 2 c 2 c 2 a 2 b 2 25 9 16
c 4
Из чертежа видно, что для гиперболы:
сг 5, aг 4
Воспользуемся соотношением между параметрами гиперболы:
c 2 a 2 b 2 b 2 c 2 a 2 25 16 9 b 3
2
2
x
y
x2 y2
1
1
a2 b2
16 9

16.

.
Написать уравнение прямой, проходящей через правый фокус
эллипса 9x 2 25 y 2 225 и перпендикулярной к прямой 3 x y 3 0
l : 3x y 3 0
x2 y2
1
25 9
3x y 3
c 2 a 2 b2 25 9 16 c 4
F2 4, 0 y y1 k x x1
k2
1
k1
A
3
l : 3 x y 3 0 kl 3
B
1
F2 M l k F2 M
1
y 0 x 4
3
3y x 4
x 3y 4 0
1
1
1
kl
3 3
x y
1
1 3

17.

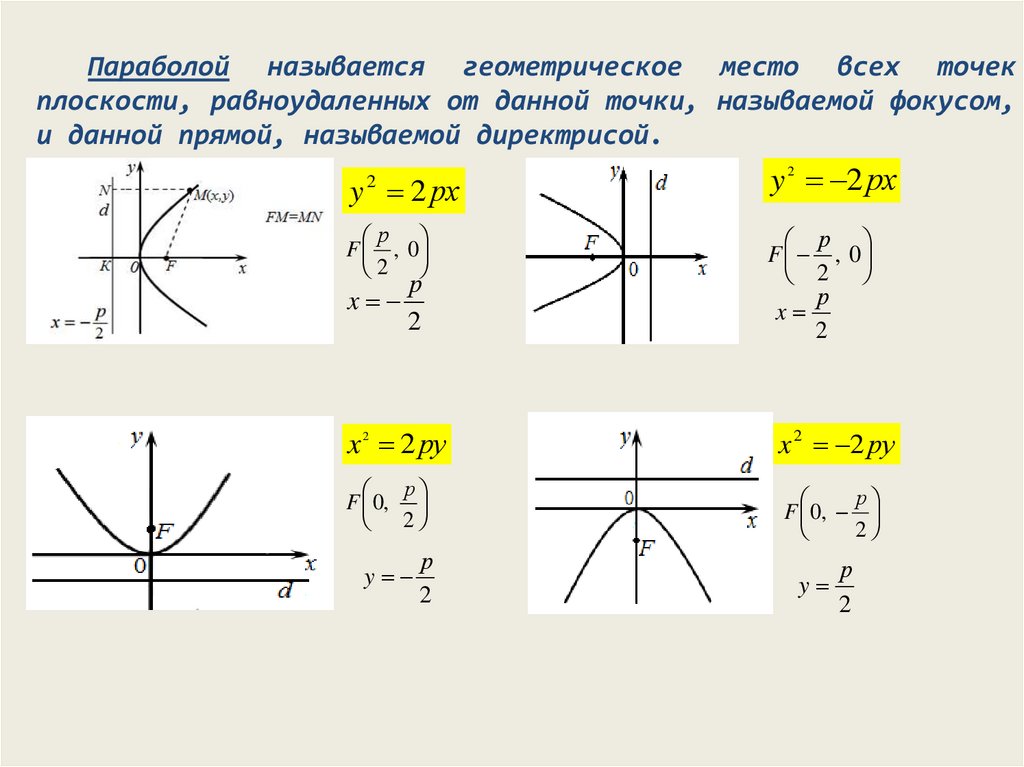
Параболой называется геометрическое место всех точек
плоскости, равноудаленных от данной точки, называемой фокусом,
и данной прямой, называемой директрисой.
y 2 рx
2
р
F , 0
2
x
р
2
y 2 2 рx
р
F , 0
2
р
x
2
x 2 2 рy
x 2 2 рy
р
F 0,
2
р
F 0,
2
y
р
2
y
р
2

18.

Составить уравнение параболы с вершиной в начале
координат, если:
1)
Парабола расположена справа от оси Оу и p=5;
2)
Парабола расположена справа от оси Оу и проходит
через точку A(3,-6);
3)
Парабола расположена ниже оси Ох и p=3 ;
4)
Парабола расположена выше оси Ох и проходит через
точку A(-5,2) ;
5)
Фокус параболы имеет координаты F(-2,0) ;
6)
Директриса задана уравнением 2y+5=0 .
6) 2 у 5 0 y
1)
y 2 рx, p 5 y 10 x
2)
y 2 2 рx, ( 6) 2 2 p 3 p 6 y 2 12 x
3)
x 2 2 рy, p 3 x 2 6 y
4)
x 2 2 рy, ( 5) 2 2 p 2 p
5)
2
y 2 2 рx
2
5
2
x 2 2 рy
y
25
25
x2
y
4
2
p
F , 0
p
2, p 4 y 2 8 x
2
2
F 2, 0
р
р 5
p 5
2
2 2
x 2 10 y

19.

Определить координаты фокуса и составить уравнение 2
y 2 рx
директрисы каждой из парабол:
1) y 2 24 x
F 6, 0 , х 6
p
2 p 24, p 12, 6
2
y 2 2 рx
2) y 2 12 x
3)
x2 4 y
2 p 12, p 6,
2 p 4, p 2,
p
3
2
F 3, 0 , х 3
p
1
2
p
F , 0
2
p
x
2
F 0, 1 , у 1
x 2 2 рy
4)
x 2 32 y 2 p 32, p 16,
p
8
2
F 0, 8 , у 8
p
F 0,
2
p
y
2
p
F , 0
2
p
x
2
x 2 2 рy
p
F 0,
2
p
y
2