Потенциальная помехоустойчивость. Лекции №3

1.

2.

Потенциальная помехоустойчивость
Помехоустойчивость РТС - способность системы передавать
и
восстанавливать
(обрабатывать)
информацию,
заключенную в радиосигналах, с заданной достоверностью
при наличии помех.
Потенциальная
помехоустойчивость
предельно
достижимая помехоустойчивость при заданных сигналах и
помехах
Реальная помехоустойчивость — это помехоустойчивость
РТС или отдельных ее звеньев с учетом реального
выполнения и настройки узлов канала связи (передающего и
приемного трактов, радиоканала, кодека, модема и т. д.)

3.

Потенциальная помехоустойчивость
Оптимальная РТС - система, реализующая потенциальную
помехоустойчивость в заданном комплексе помех
Оптимальная РТС =
оптимальный приемник
оптимальный
передатчик
+

4.

Задачи теории связи
Прямая задача:
по заданному комплексу помех при заданных ограничениях
определить оптимальный сигнал и способ приема и синтезировать
оптимальные передатчик и приемник;
Обратная задача:
для заданной системы передачи, при заданных ограничениях
определить эффективную помеху и синтезировать её генератор.

5.

Задачи РТС
Обнаружение сигнала и различение сигналов;
Оценка параметров сигналов;
Фильтрация сигналов;
Разрешение и распознавание сигналов

6.

Модель и статистические характеристики
РТС

7.

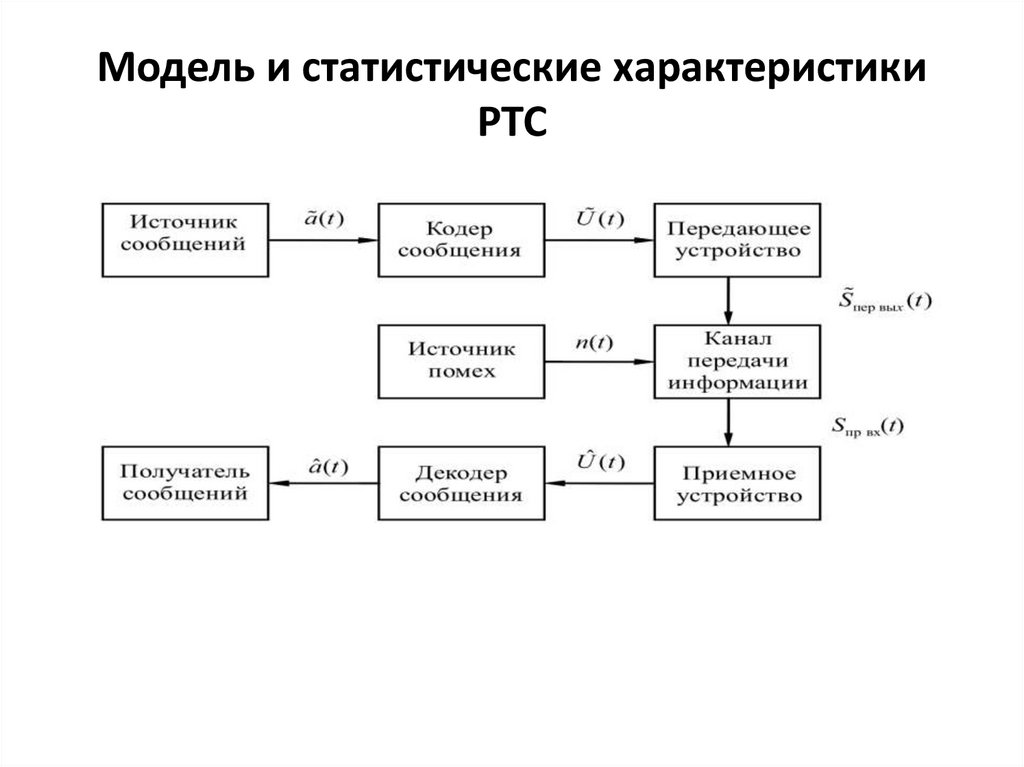
Модель и статистические характеристики
РТС
Источник сообщений: ã(t), w (ã),
Кодер: u(t)=U[ ã(t)], w(u)
Передатчик: s(t)= V[u(t),f(t)], w(s), f(t) – ВЧ сигнал
Радиоканал: sвх.пр.=K[s(t), n(t)], w(n), w(sвх.пр), при
известном s(t)
Приемник: û(t)=W[sвх.пр], â(t)=U-1[û(t)]
ꓲꓲâ(t)-ã(t)ꓲꓲ=min

8.

Постановка задачи оптимизации
• Описать модель РТС
• Выбрать критерий оптимизации

9.

Критерий среднего риска
P(S) - вероятности наличия сигнала обнаружение сигнала;
P(O) – вероятность отсутствия сигнала;
P(реш O|S) – ошибочное решение при наличии сигнала;
P(реш S|O) – ошибочное решение при отсутствии сигнала.
Цs 0 P реш O S P S Цs 0 P реш S O P O
min

10.

Критерий среднего риска
Сообщение с множеством состояний А = {а}
Ц ai , aˆ j P ai , aˆ j
k 1 k 1
i 0 j 0
P ai , a j P ai P aˆ j ai
P ai Ц ai , aˆ j P aˆ j
k 1
k 1
i 0
j 0
ai
Ц ai , aˆ j P aˆ j
k 1
j 0
ai
ai
.

11.

Оптимальное различение сигнала
Дано множество сигналов A = {a} от источника
информации.
Задача: Определить правило оптимального принятия
решения при приеме сигналов (V), если на выходе
приемника наблюдаем сигналы bj, j=1,2,3, ..., m (m>k).
Известны:
a) P(ai), i=1,2,3 … k.
b) форма и параметры (кроме номера i) всех k
сигналов, которые соответствуют возможным
состояниям источника информации в месте приема;
c) вероятностные характеристики помех W(n)
d) характер их взаимодействия в канале передачи
информации с ожидаемыми сигналами sвх пр=K(si,n)

12.

Оптимальное различение сигнала
Число возможных реализаций принятого сигнала
существенно превышает k-алфавит источника. Задача
приемника - разделить все пространство реализации
S
на k подпространств, принять решение о передаче jго сигнала только в случае попадания реализации s в
j-е пространство. Приемник будет оптимальным , если
такое разбиения пространства S на k подпространств
обеспечивает минимальные средние потери.
в х пр
в х пр
в х пр

13.

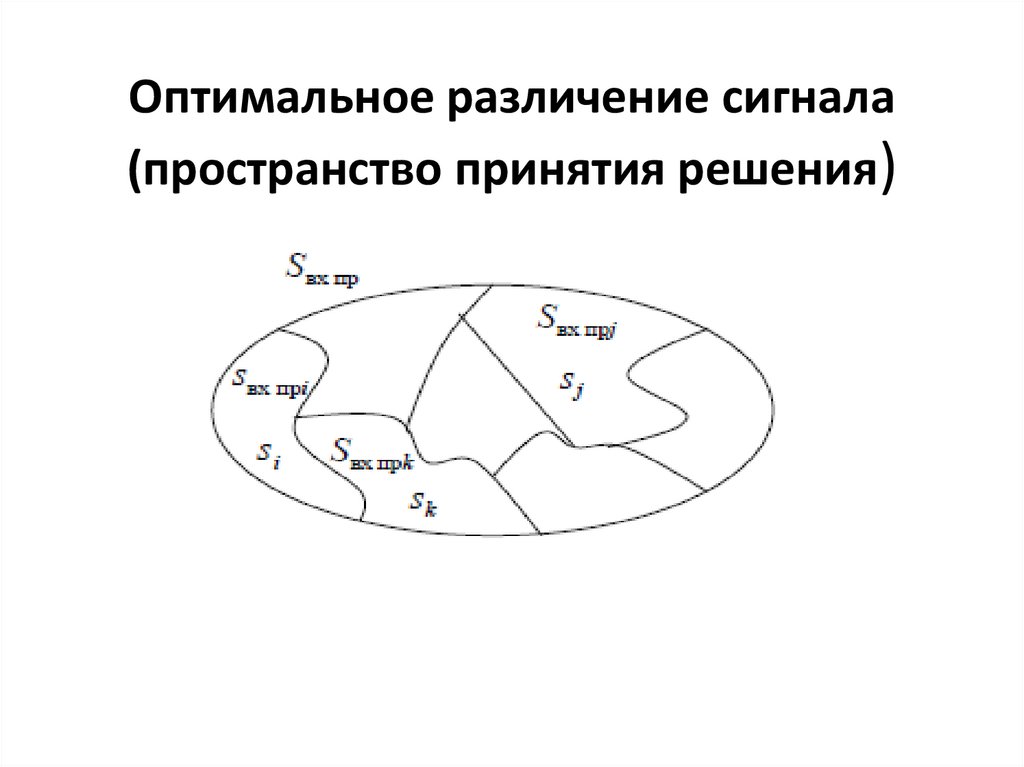
Оптимальное различение сигнала
(пространство принятия решения)

14.

Оптимальное различение сигнала
d Sв х пр
решающая функция. Тогда d S b , если
в х пр
j
S в х пр S в х прj
.
Из-за помех, вектор S при передаче сигнала Si может оказаться
в любой точке пространства S , причем точка необязательно
будет принадлежать области переданного сигнала (ошибочные
решения). Задача оптимизации оператора V – разделить
пространство S
на k областей таким образом, чтобы
обеспечивался минимальный средний риск при заданной
функции потерь.
в х пр
в х пр
в х пр
Оптимальная система приема сигналов делит на области
0, ..., k-1 так, что выполнялись условия:
Ц ai , aˆ j P ai , aˆ j min
k 1 k 1
i 0 j 0
.
Sв х прi
,i=

15.

Оптимальное различение сигнала
Если известна статистика помех и характер взаимодействия
сигнала известной формы и помехи в канале передачи
информации, то можно вычислить условную плотность
распределения принятых S для каждого передаваемого
сигнала W S S (функция правдоподобия)
в х пр
в х пр
i
Пример функции правдоподобия

16.

Оптимальное
различение
сигнала
.
P aˆ j ai
W Sвх пр Si dSвх пр
S вх пр j
W Sвх пр ai dSвх пр
S вх пр j
Тогда средний риск определиться, как:
Ц aˆ j , ai P ai
k 1 k 1
j 0 i 0
k 1
W Sвх пр
ai dSвх пр
S вх пр j
dSвх пр Ц aˆ j , ai P Sвх пр i W Sвх пр ai
dSвх пр Ц aˆ j , ai P ai W Sвх пр ai .
j 0 S вх пр j
k 1
i 0
k 1
i 0
S вх пр j
Значение среднего риска минимально, если каждой
реализации S оценка â выбирается таким образом, из всех K
сумм вида Ц a , a P a W S a , k 0,1,..., k 1 , наименьшей является j-я,
в х пр
k
i
i
i
вх пр
i
i
т.е. при фиксированном j удовлетворяется система уравнений,
состоящая из k-1 неравенств
Ц aˆ j , ai P ai W Sвх пр ai Ц aˆk , ai P ai .
k 1
k 1
i 0
i 1
или

17.

Оптимальное
Ц aˆ j , ai P ai Sвх пр Ц aˆk , ai P ai Sвх пр , , k 0,1,..., k 1; j k .
k 1
k 1
i 0
i 0
P ai S в х пр
-
апостериорная вероятность i-го состояния
источника информации.

18.

Оптимальное различение сигнала
При k=0,1 различитель двоичных сигналов (оптимальный приемник двоичных сигналов) должен принимать
решение, что k=1, если
Ц aˆ1 , a0 P a0 W Sвх пр a0 Ц aˆ1 , a1 P a1 W Sвх пр a1
Ц aˆ0 , a0 P a0 W Sвх пр a0 Ц aˆ0 , a1 P a1 W Sвх пр a1 .
Откуда получим
Sвх пр
W Sвх пр a1
Ц a1, a0 Ц a0 , a0 P a0 ,
W Sвх пр a0 Ц a0 , a1 Ц a1, a1 P a1
где W Sвх пр a1 W Sвх пр a0 Sвх пр - отношение правдоподобия,
a, - пороговый уровень

19.

Критерий Неймана-Пирсона
S в х пр 0
- состояние «0» (отсутствие сигнала);
Sв х пр1
- состояние «1» (наличие сигнала на входе приемника)
Принятие решения – выбор в пользу одной из возможных
гипотез:
H0 – гипотеза «сигнала нет»
H1 – гипотеза «сигнал есть»
При принятии решения возможны 4 ситуации:
1)Сигнала нет ( S
в х пр 0
2) Сигнала нет ( S
), решение - сигнал есть (H1 )
в х пр 0
), решение - сигнала нет (H0 )
3) Сигнал есть ( S ), решение – сигнала нет (H0)
в х пр1
4)Сигнал есть ( S ), решение – сигнал есть (H1)
в х пр1

20.

Критерий Неймана-Пирсона
P Sвх пр1 H1
- вероятность принятия решения о наличии сигнала
при его реальном отсутствии. Ошибка второго рода (ошибка
ложной тревоги)
P Sвх пр1 H1
- вероятность принятия решения об отсутствии сигнала
при его реальном наличии. Ошибка первого рода (ошибка
пропуска сигнала)
Sвх пр W Sвх пр H0 W Sвх пр H1 h

21.

Критерий Вальда
Критерий Неймана – Пирсона используется при
фиксированном объеме выборки S . (одно наблюдение)
в х пр
Критерий Вальда - объем выборки заранее не известен (время
наблюдения не ограничено).
k Sвх пр W Sвх пр 1,..., Sвх пр k 0 W Sвх пр a ,..., Sвх пр k 1
– отношение правдоподобия на
k-м шаге наблюдения; d S – правило принятия решения.
Тогда процедура обнаружения определяется как:
в х пр
d 0 , k a;
d Sв х пр1 ,..., Sв х прk d1 , k b; k 1,2,...,
d , a b,
k
пр
a и b – нижний и верхний пороги; d0 и d1 – решение «нет цели»
и «есть цель» соответственно; dпр – решение о продолжении
наблюдения.
Величины a и b определяются по заданным значениям
вероятностей ложной тревоги и пропуска цели