Похожие презентации:
Электромагнитная природа света. Интерференция света. Лекции 12-13
1. Лекции 12-13. 2017. Электромагнитная природа света. Интерференция света
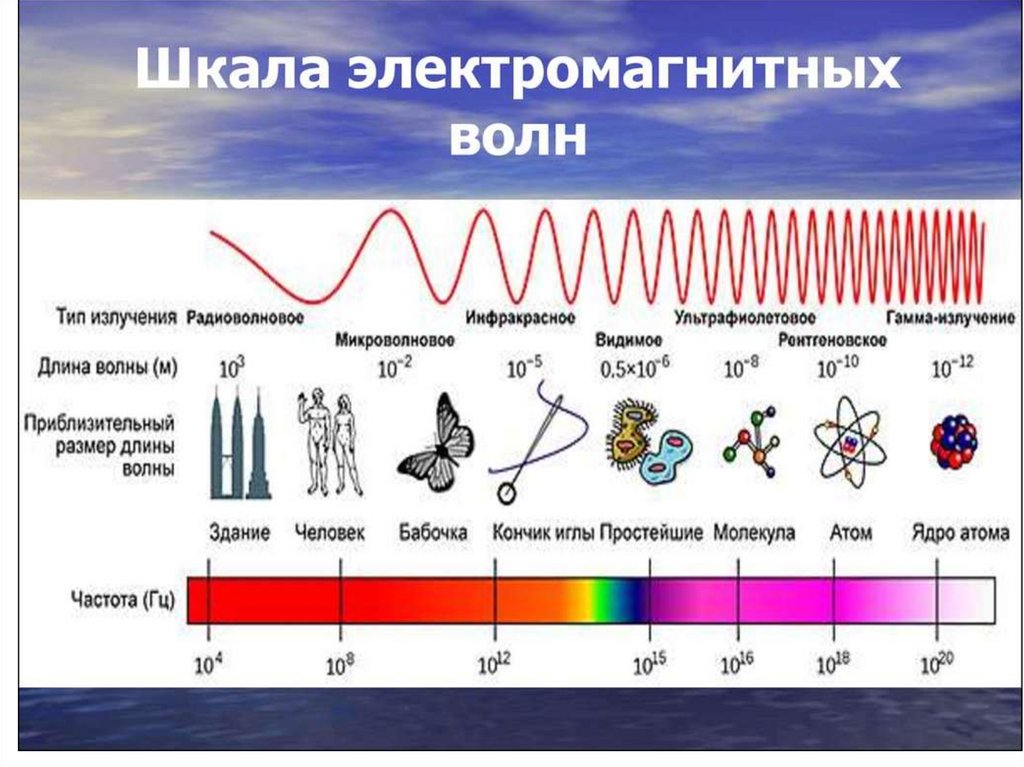
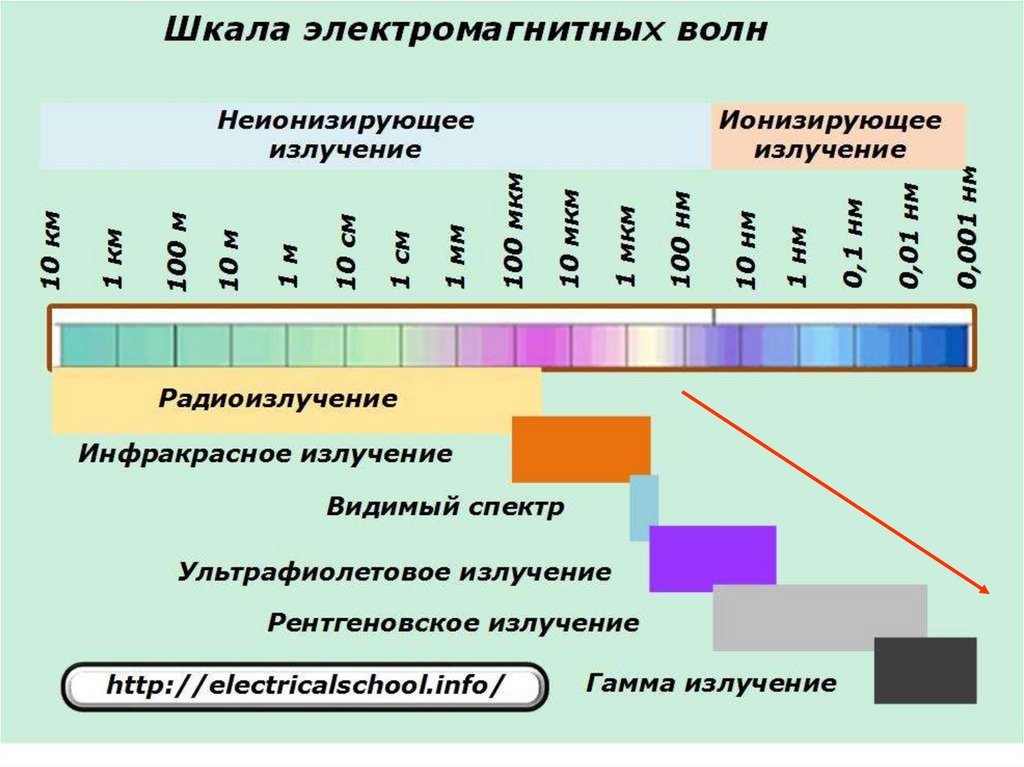
1. Шкала электромагнитных излучений.Оптическое излучение, его интенсивность.
2. Интерференция электромагнитных волн.
3. Расчет интерференционной картины с
двумя источниками.
4. Пространственно-временная
когерентность.
Чуев А.С.-2020 г.
1
2.
Свет – самое темное место в физикеИзвестное убеждение
самих физиков
Чуев А.С.-2020 г.
2
3.
Чуев А.С.-2020 г.3
4.
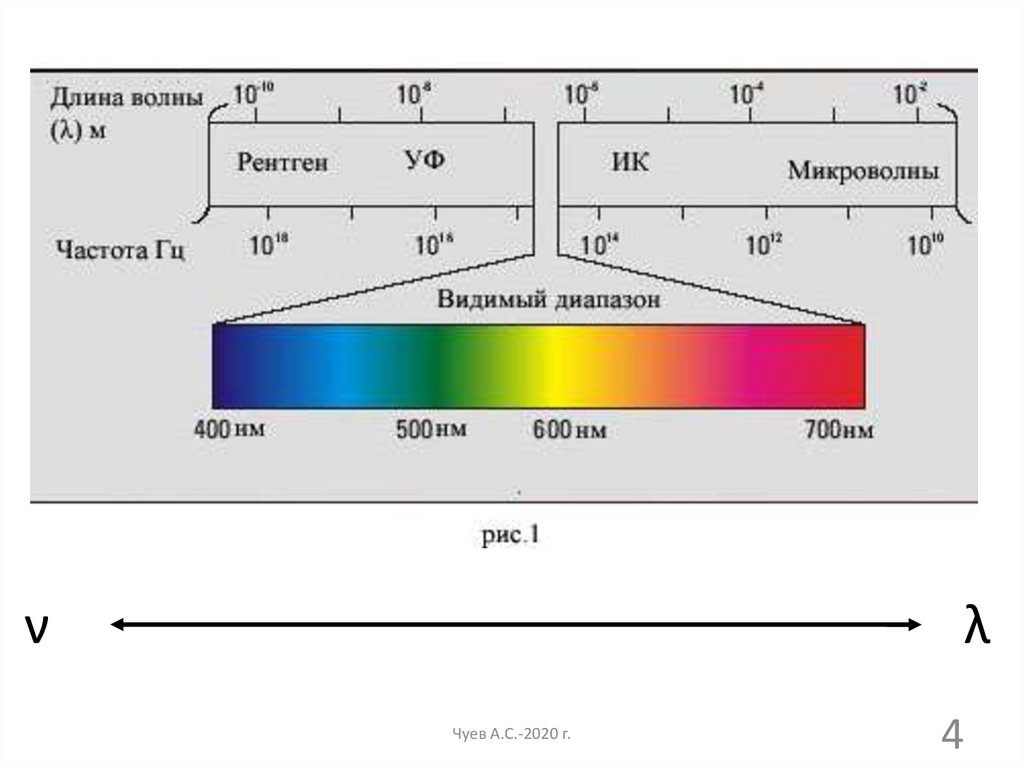
νλ
Чуев А.С.-2020 г.
4
5.
Чуев А.С.-2020 г.5
6.
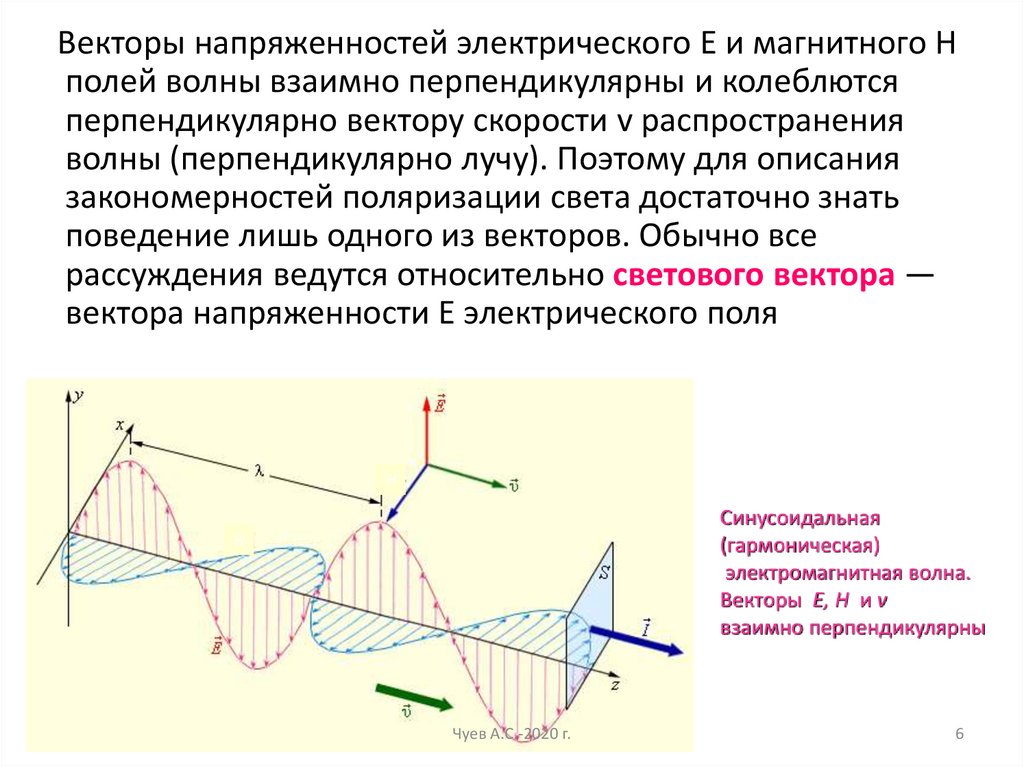
Векторы напряженностей электрического Е и магнитного Нполей волны взаимно перпендикулярны и колеблются
перпендикулярно вектору скорости v распространения
волны (перпендикулярно лучу). Поэтому для описания
закономерностей поляризации света достаточно знать
поведение лишь одного из векторов. Обычно все
рассуждения ведутся относительно светового вектора —
вектора напряженности Е электрического поля
Н
Синусоидальная
(гармоническая)
электромагнитная волна.
Векторы Е, Н и v
взаимно перпендикулярны
Н
Чуев А.С.-2020 г.
6
7.
• Свет представляет собой суммарноеэлектромагнитное излучение множества
атомов. Атомы же излучают световые
волны независимо друг от друга, поэтому
световая волна, излучаемая телом в целом,
характеризуется всевозможными
равновероятными колебаниями светового
вектора
луч перпендикулярен
плоскости рисунка
Чуев А.С.-2020 г.
7
8.
Равномерное распределение векторов Еобъясняется большим числом атомарных
излучателей, а равенство амплитудных значений
векторов Е — одинаковой (в среднем)
интенсивностью излучения каждого из атомов.
Свет со всевозможными равновероятными
ориентациями вектора Е называется
естественным.
Свет , в котором направления колебаний
светового вектора каким-то образом
упорядочены, называется поляризованным.
Чуев А.С.-2020 г.
8
9.
Если в результате каких-либо внешнихвоздействий появляется преимущественное (но
не исключительное!) направление колебаний
вектора Е, то имеем дело с частично
поляризованным светом.
Свет, в котором вектор Е (и, следовательно, Н)
колеблется только в одном направлении,
перпендикулярном лучу, называется линейно
поляризованным
Чуев А.С.-2020 г.
9
10.
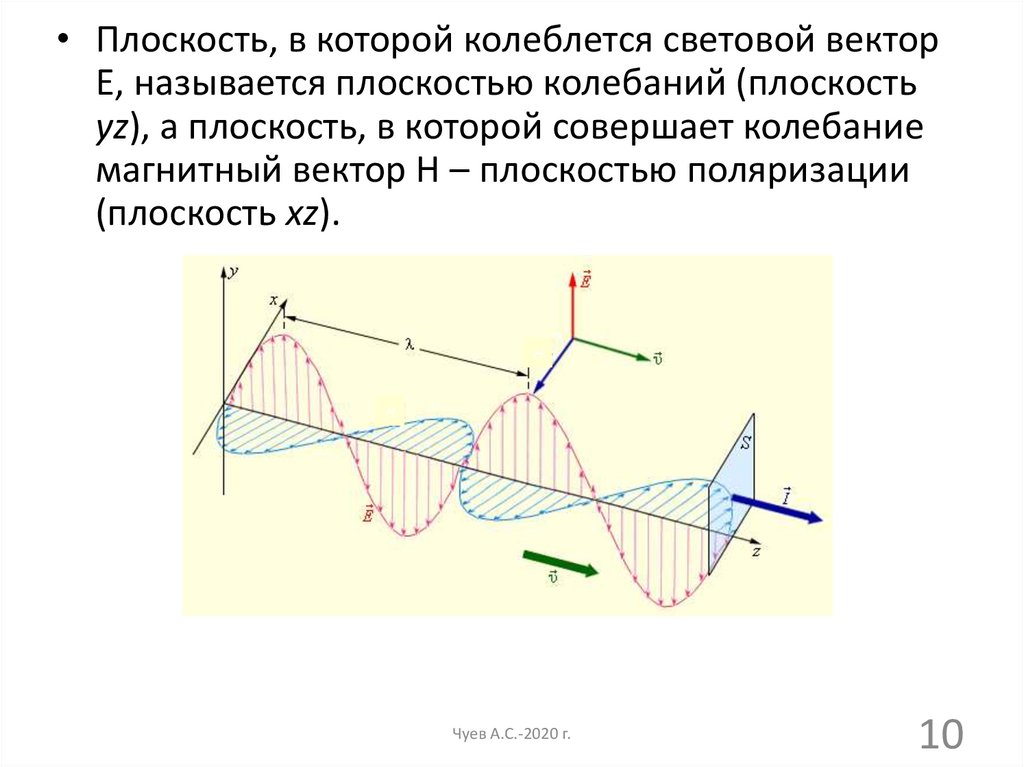
• Плоскость, в которой колеблется световой векторЕ, называется плоскостью колебаний (плоскость
yz), а плоскость, в которой совершает колебание
магнитный вектор Н – плоскостью поляризации
(плоскость xz).
Н
Н
Чуев А.С.-2020 г.
10
11.
• Плоскополяризованный свет является предельнымслучаем эллиптически поляризованного света — света,
для которого вектор Е (вектор Н) изменяется со
временем так, что его конец описывает эллипс,
лежащий в плоскости, перпендикулярной лучу.
• Если эллипс поляризации вырождается в прямую (при
разности фаз φ, равной нулю или π), то имеем дело с
рассмотренным выше плоскополяризованным светом,
если в окружность (при Δφ = ±π/2 и равенстве
амплитуд складываемых волн), то имеем дело с
циркулярно поляризованным (поляризованным по
кругу) светом.
Чуев А.С.-2020 г.
11
12.
Чуев А.С.-2020 г.12
13.
Чуев А.С.-2020 г.13
14.
Чуев А.С.-2020 г.14
15.
Круговая поляризацияЧуев А.С.-2020 г.
15
16.
Начало конспектированияИнтенсивность излучения.
Закон Малюса
Чуев А.С.-2020 г.
16
17.
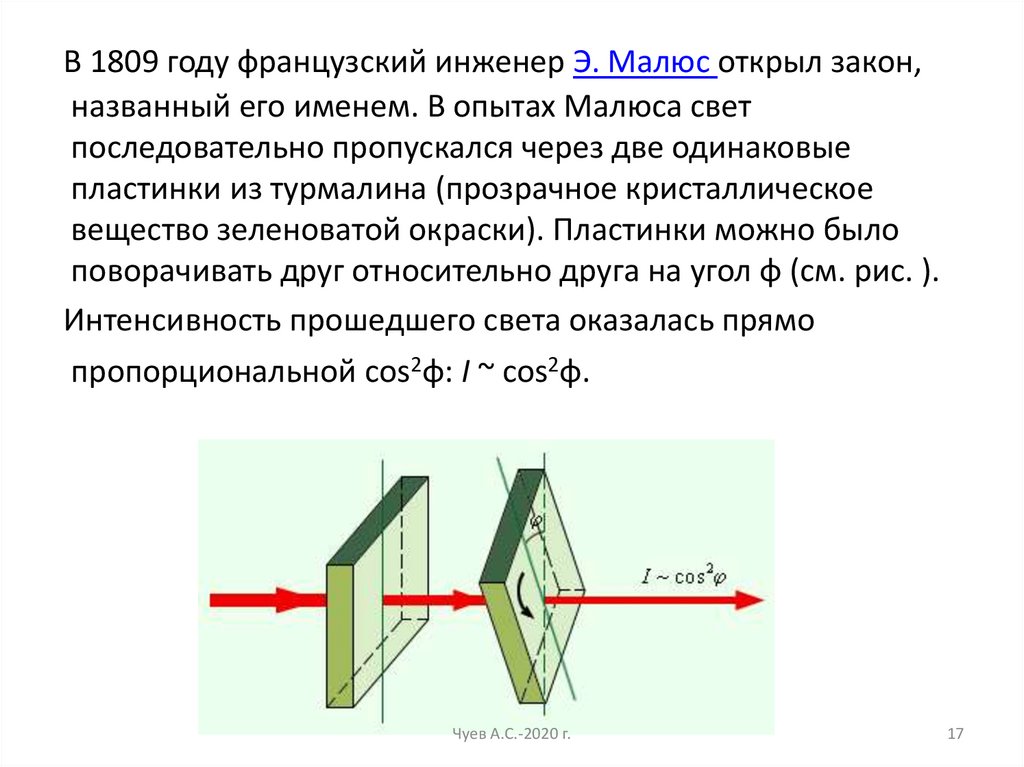
В 1809 году французский инженер Э. Малюс открыл закон,названный его именем. В опытах Малюса свет
последовательно пропускался через две одинаковые
пластинки из турмалина (прозрачное кристаллическое
вещество зеленоватой окраски). Пластинки можно было
поворачивать друг относительно друга на угол φ (см. рис. ).
Интенсивность прошедшего света оказалась прямо
пропорциональной cos2φ: I ~ cos2φ.
Чуев А.С.-2020 г.
17
18.
Чуев А.С.-2020 г.18
19.
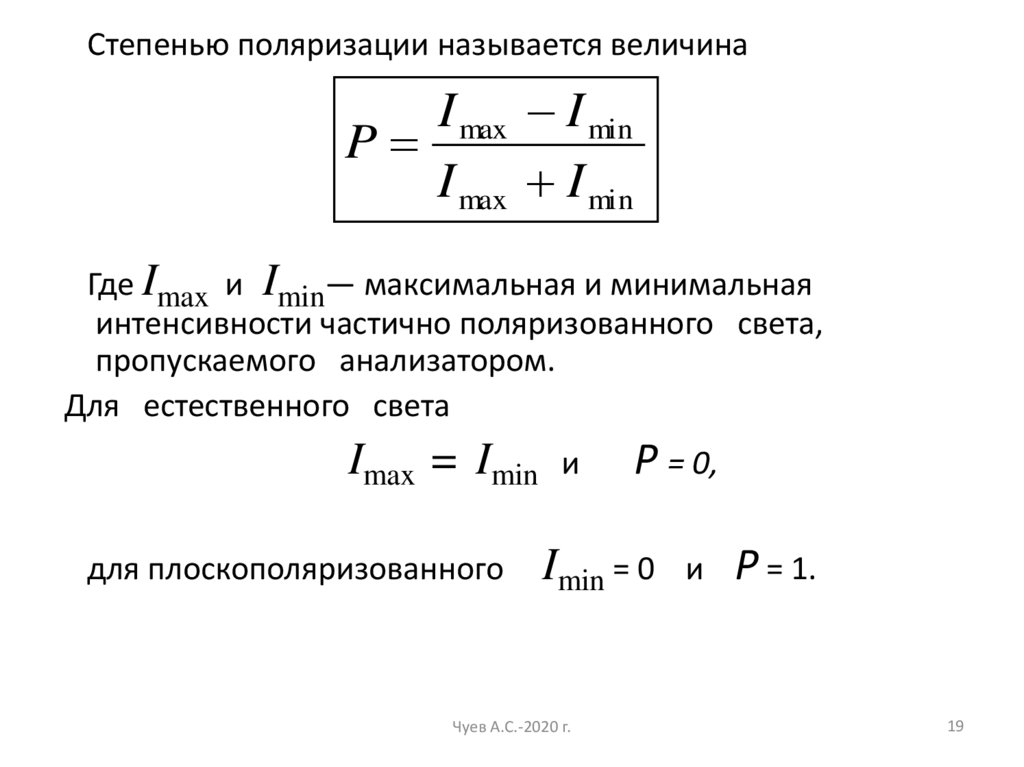
Степенью поляризации называется величинаI max I min
P
I max I min
Где Imax и Imin— максимальная и минимальная
интенсивности частично поляризованного света,
пропускаемого анализатором.
Для естественного света
Imax = Imin
для плоскополяризованного
и
Р = 0,
Imin = 0
Чуев А.С.-2020 г.
и
P = 1.
19
20.
Чуев А.С.-2020 г.20
21.
Чуев А.С.-2020 г.21
22.
Воздух-стекло, II - поляризацияЧуев А.С.-2020 г.
22
23.
Воздух-стекло, T - поляризацияЧуев А.С.-2020 г.
23
24.
Стекло-воздух, II - поляризацияЧуев А.С.-2020 г.
24
25.
Стекло-воздух, T - поляризацияЧуев А.С.-2020 г.
25
26.
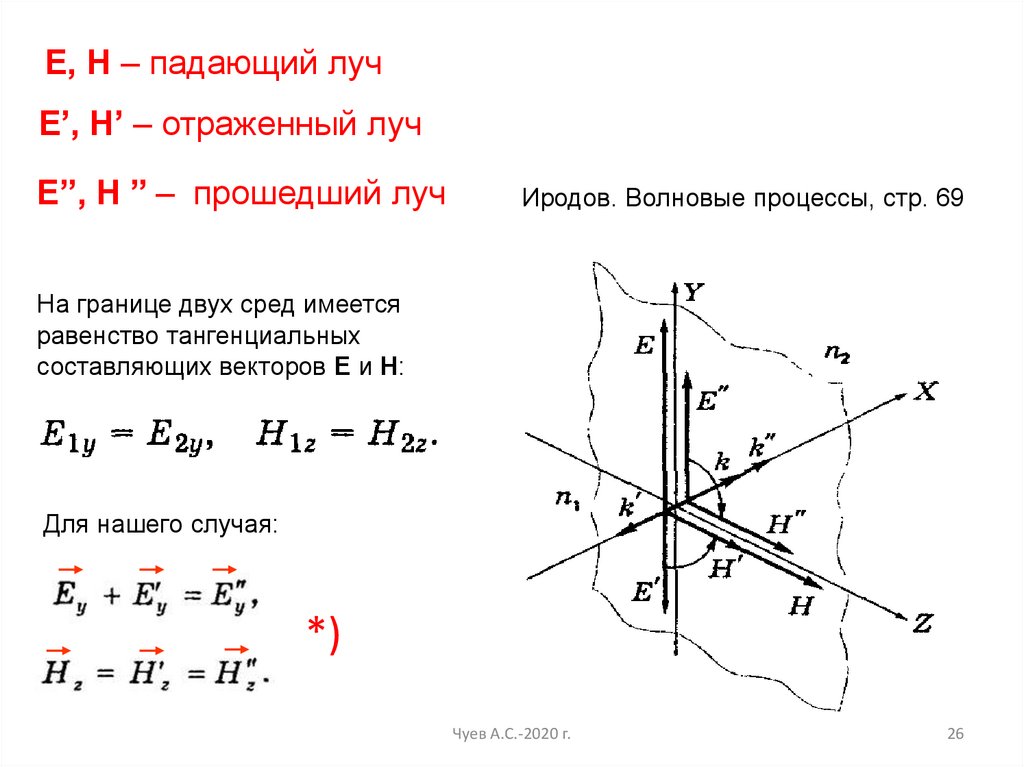
Е, Н – падающий лучЕ’, Н’ – отраженный луч
E’’, Н ’’ – прошедший луч
Иродов. Волновые процессы, стр. 69
На границе двух сред имеется
равенство тангенциальных
составляющих векторов Е и Н:
Для нашего случая:
*)
Чуев А.С.-2020 г.
26
27.
Используя соотношения:и
вытекающие из
можем записать:
С учетом *) получим:
Для отраженного Е’ и прошедшего E’’ лучей:
Чуев А.С.-2020 г.
27
28.
Чуев А.С.-2020 г.28
29.
Коэффициенты отражения и пропусканияКоэффициент отражения:
Коэффициент пропускания:
Чуев А.С.-2020 г.
29
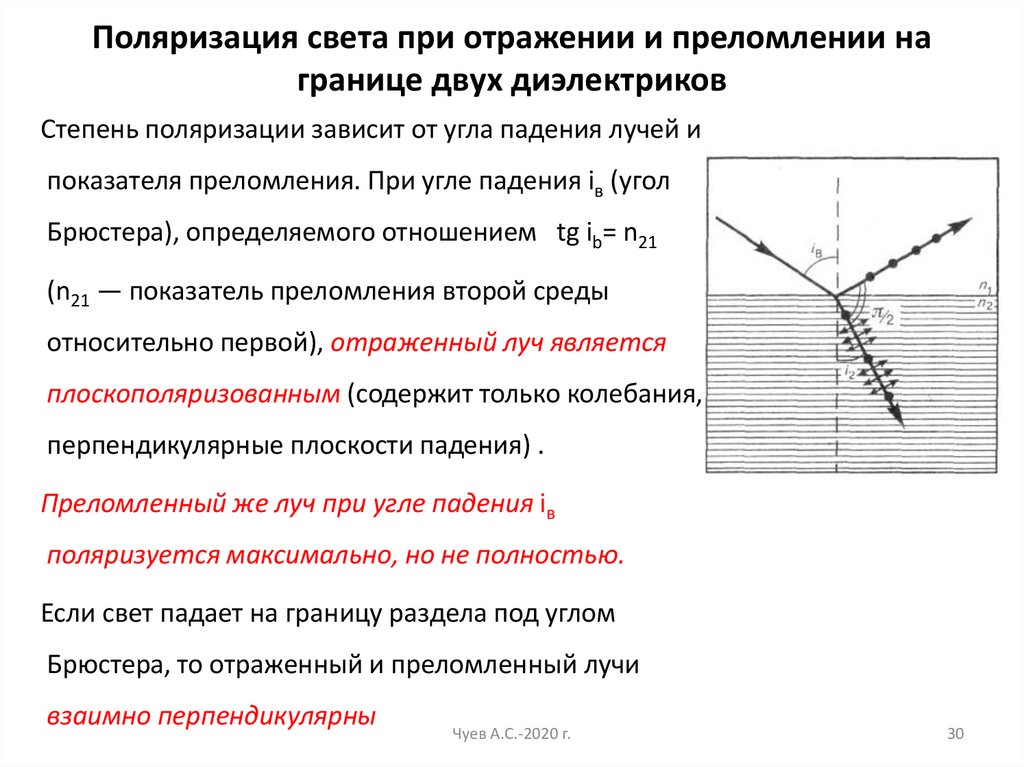
30. Поляризация света при отражении и преломлении на границе двух диэлектриков
Степень поляризации зависит от угла падения лучей ипоказателя преломления. При угле падения iв (угол
Брюстера), определяемого отношением tg ib= n21
(n21 — показатель преломления второй среды
относительно первой), отраженный луч является
плоскополяризованным (содержит только колебания,
перпендикулярные плоскости падения) .
Преломленный же луч при угле падения iв
поляризуется максимально, но не полностью.
Если свет падает на границу раздела под углом
Брюстера, то отраженный и преломленный лучи
взаимно перпендикулярны
Чуев А.С.-2020 г.
30
31.
tgib = sin ib /cos ib, n21 = sin ib /sin i2( i2 — угол преломления),
откуда cos ib = sini2.
Следовательно, ib+i2 = π/2, но i'b= ib
(закон отражения), поэтому ib + i2 = π /2.
Чуев А.С.-2020 г.
31
32.
Чуев А.С.-2020 г.32
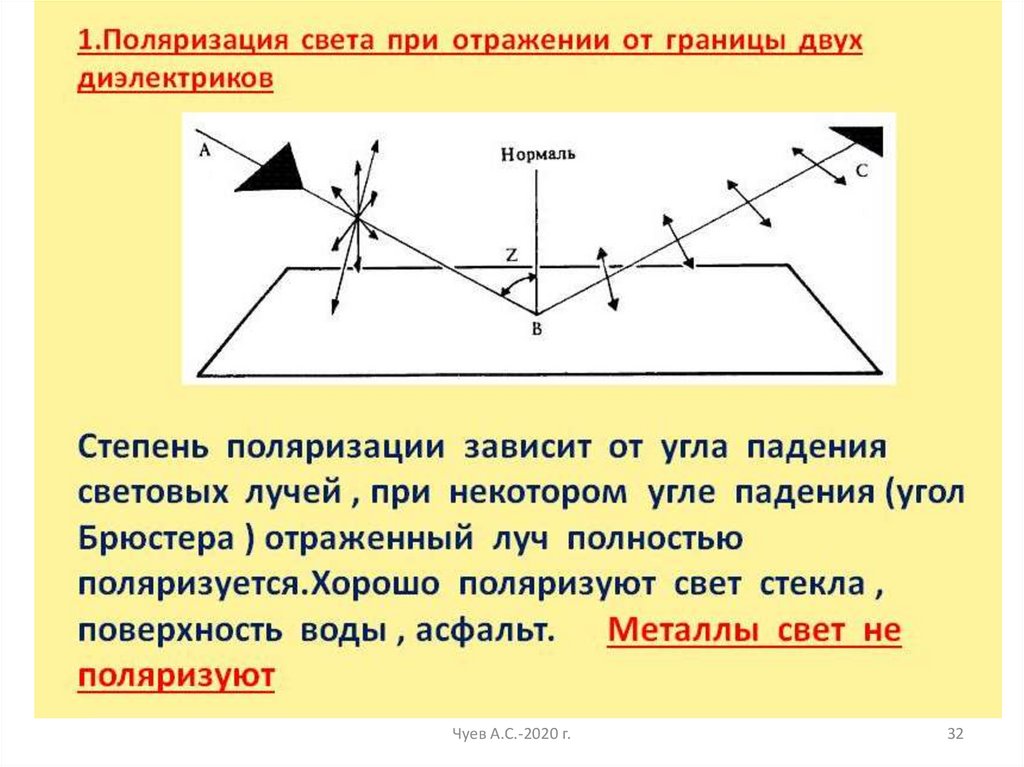
33.
Интерференция электромагнитных волнЧуев А.С.-2020 г.
33
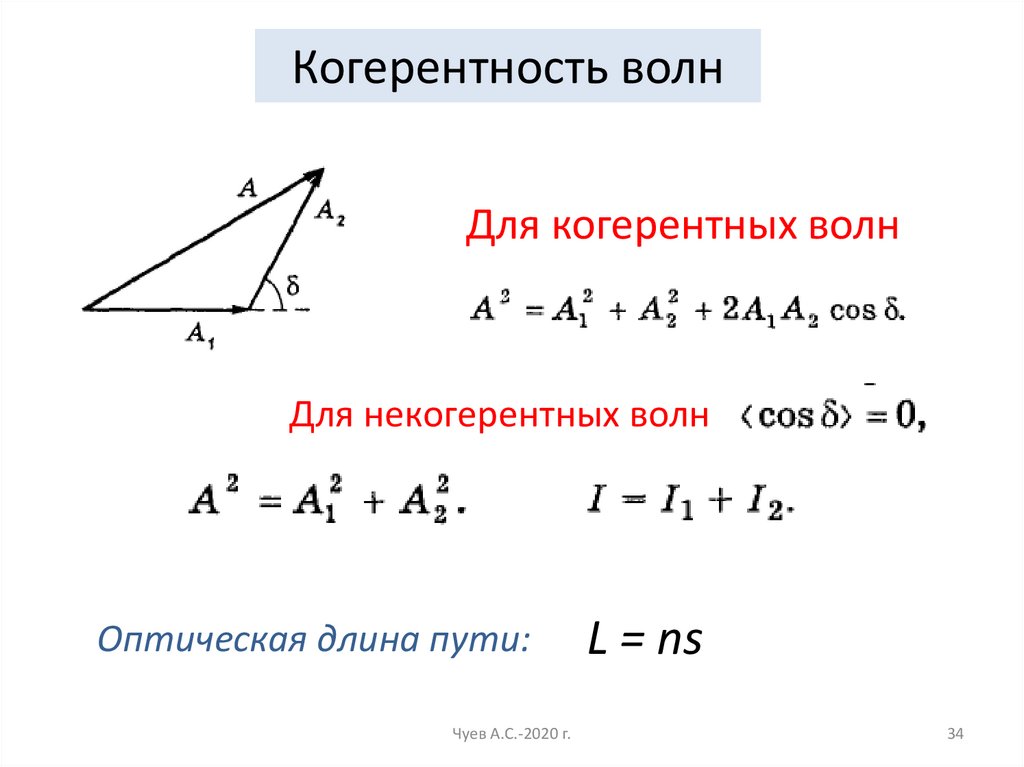
34. Когерентность волн
Для когерентных волнДля некогерентных волн
Оптическая длина пути:
Чуев А.С.-2020 г.
L = ns
34
35.
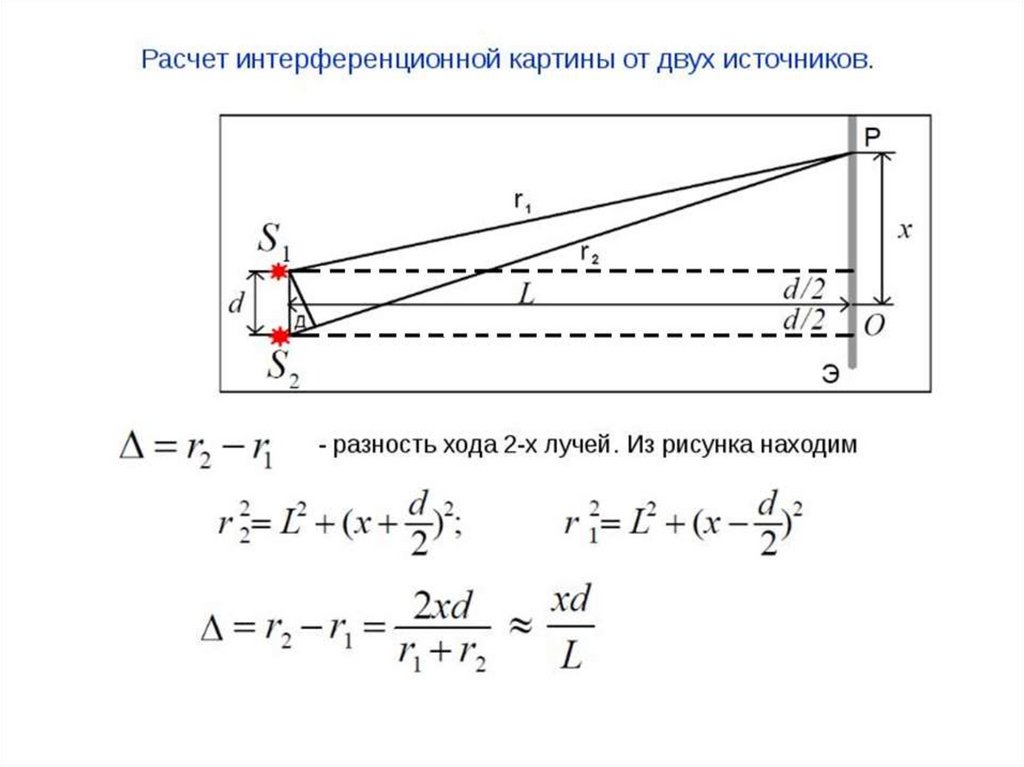
Расчет интерференционной картины от двухисточников
- оптическая разность хода
Чуев А.С.-2020 г.
35
36.
Здесь L лучше обозначить как l и обозначить угол θЧуев А.С.-2020 г.
36
37.
Чуев А.С.-2020 г.37
38.
Прии когерентности излучения двух источников
Чуев А.С.-2020 г.
38
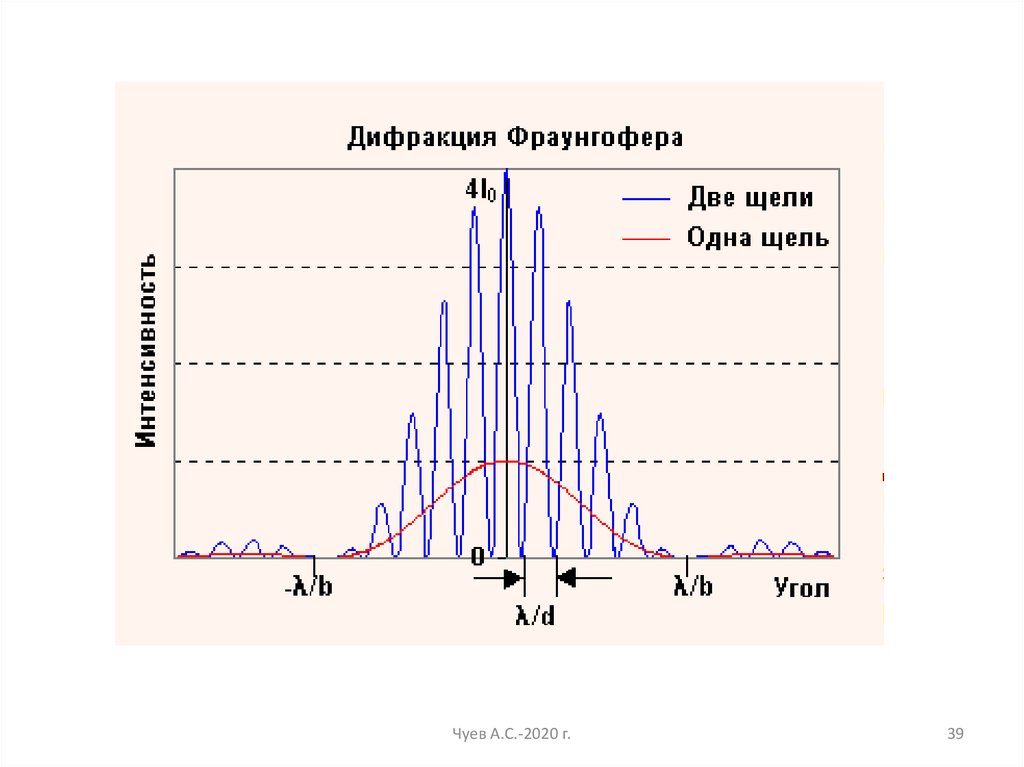
39.
Чуев А.С.-2020 г.39
40.
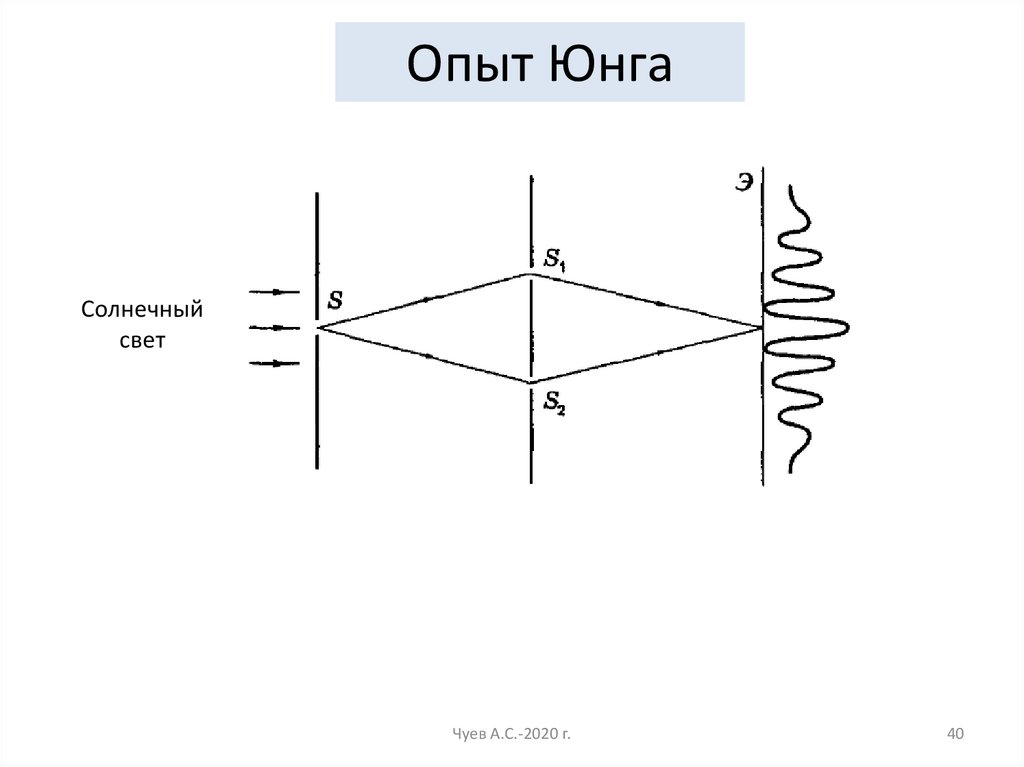
Опыт ЮнгаСолнечный
свет
Чуев А.С.-2020 г.
40
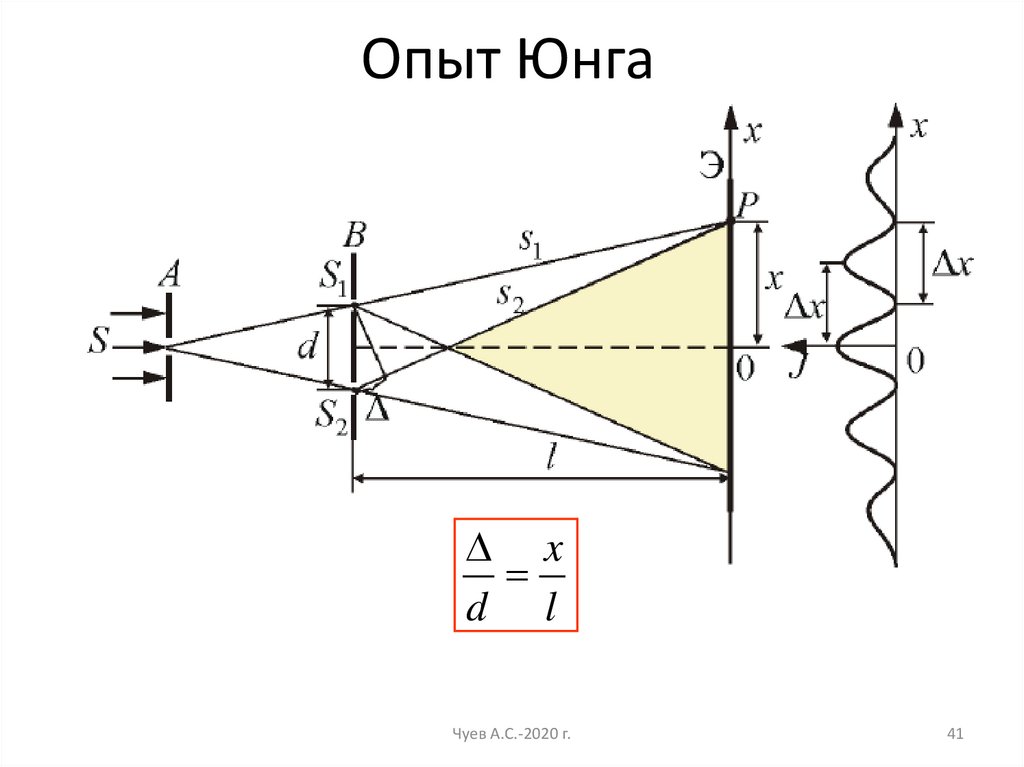
41.
Опыт Юнгаx
d l
Чуев А.С.-2020 г.
41
42.
Чуев А.С.-2020 г.42
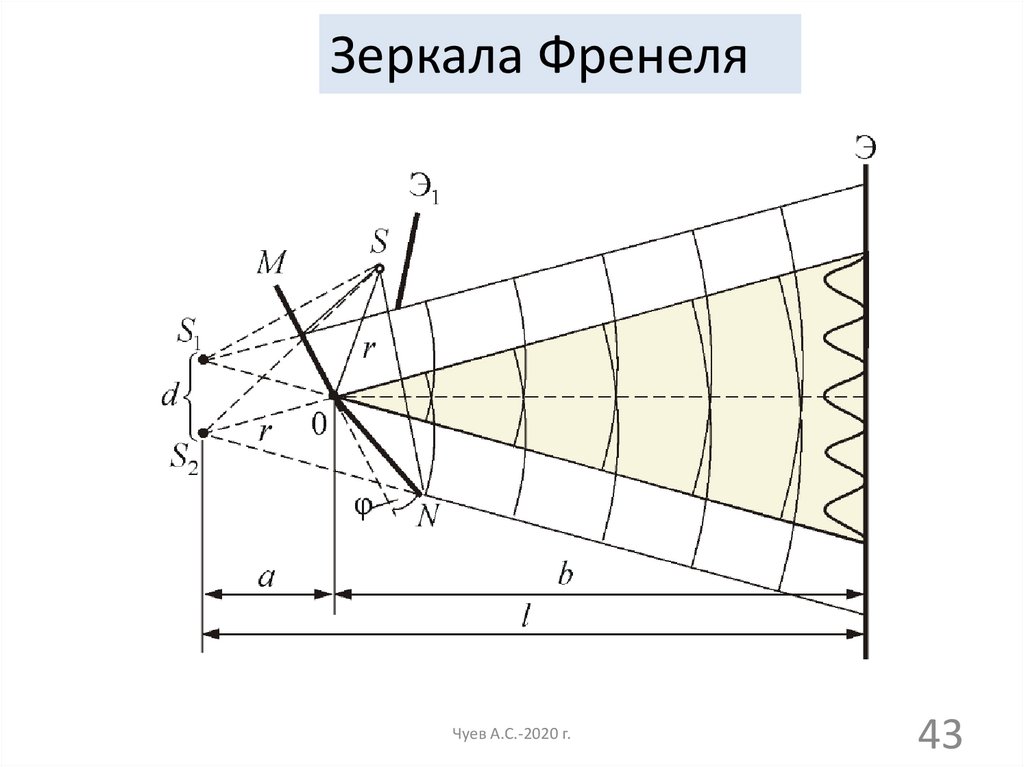
43.
Зеркала ФренеляЧуев А.С.-2020 г.
43
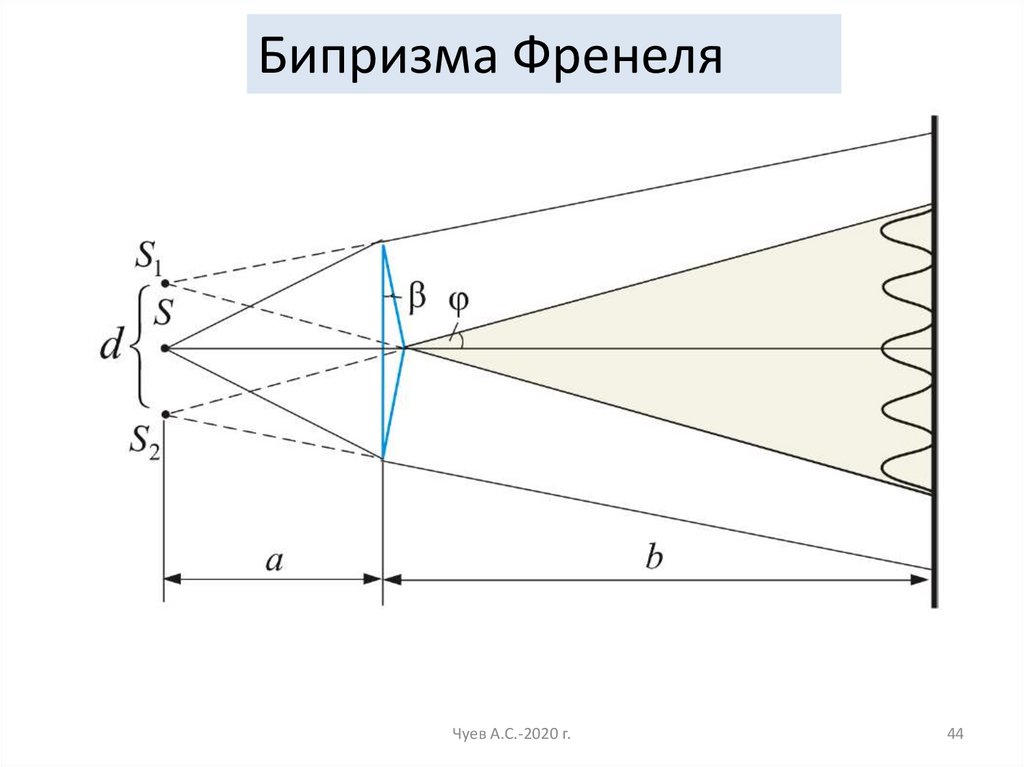
44.
Бипризма ФренеляЧуев А.С.-2020 г.
44
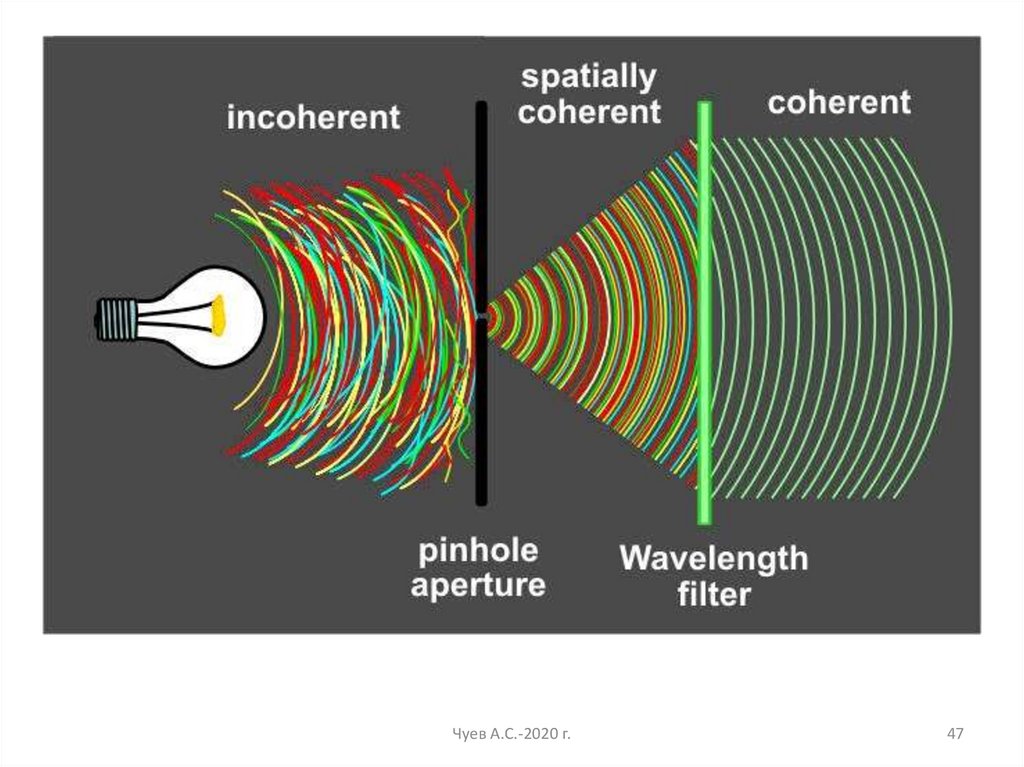
45.
Пространственно- временная когерентностьВремя когерентности:
Длина когерентности:
Ширина когерентности:
Чуев А.С.-2020 г.
45
46.
Чуев А.С.-2020 г.46
47.
Чуев А.С.-2020 г.47
48.
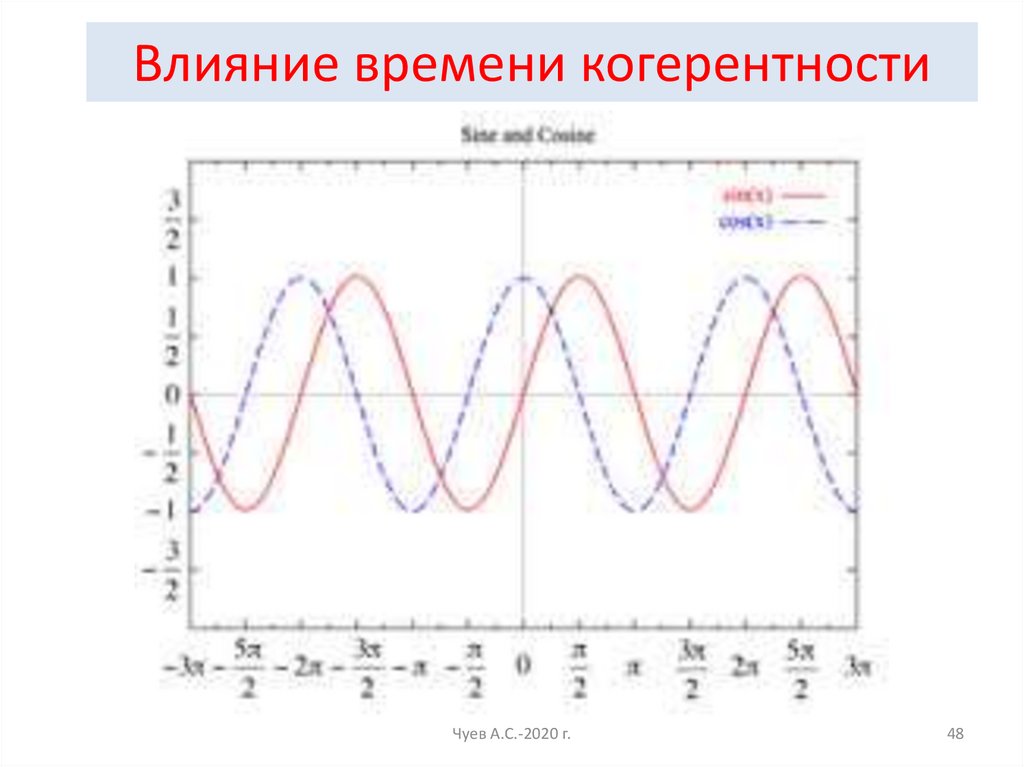
Влияние времени когерентностиЧуев А.С.-2020 г.
48
49.
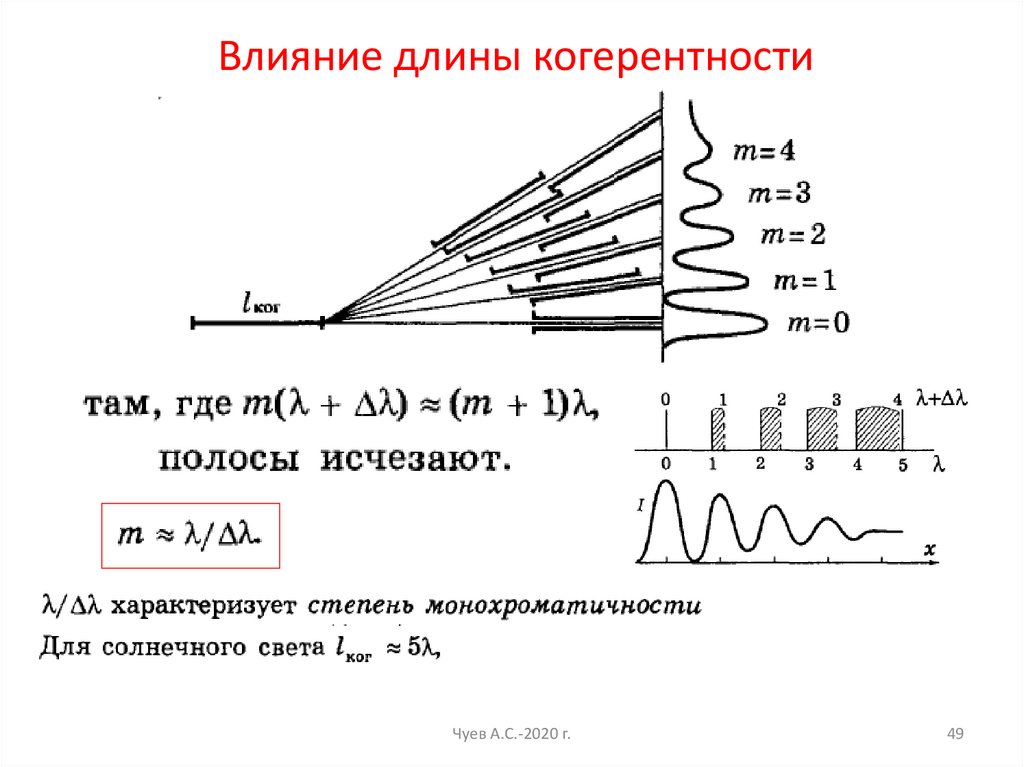
Влияние длины когерентностиЧуев А.С.-2020 г.
49
50.
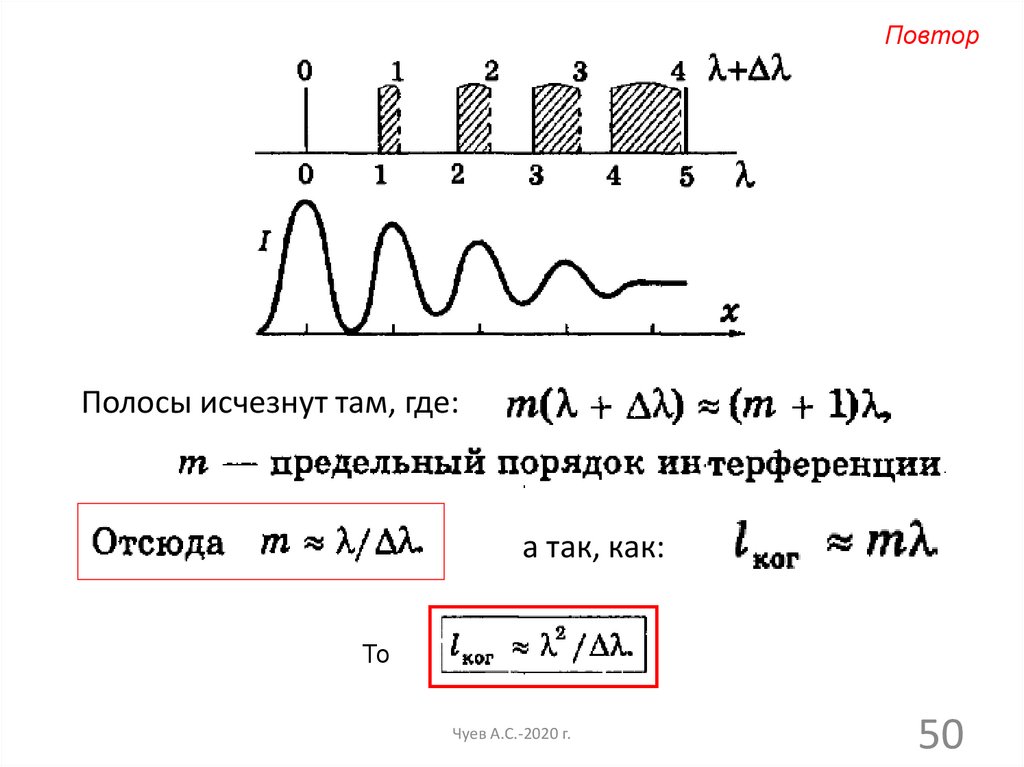
ПовторПолосы исчезнут там, где:
а так, как:
То
Чуев А.С.-2020 г.
50
51.
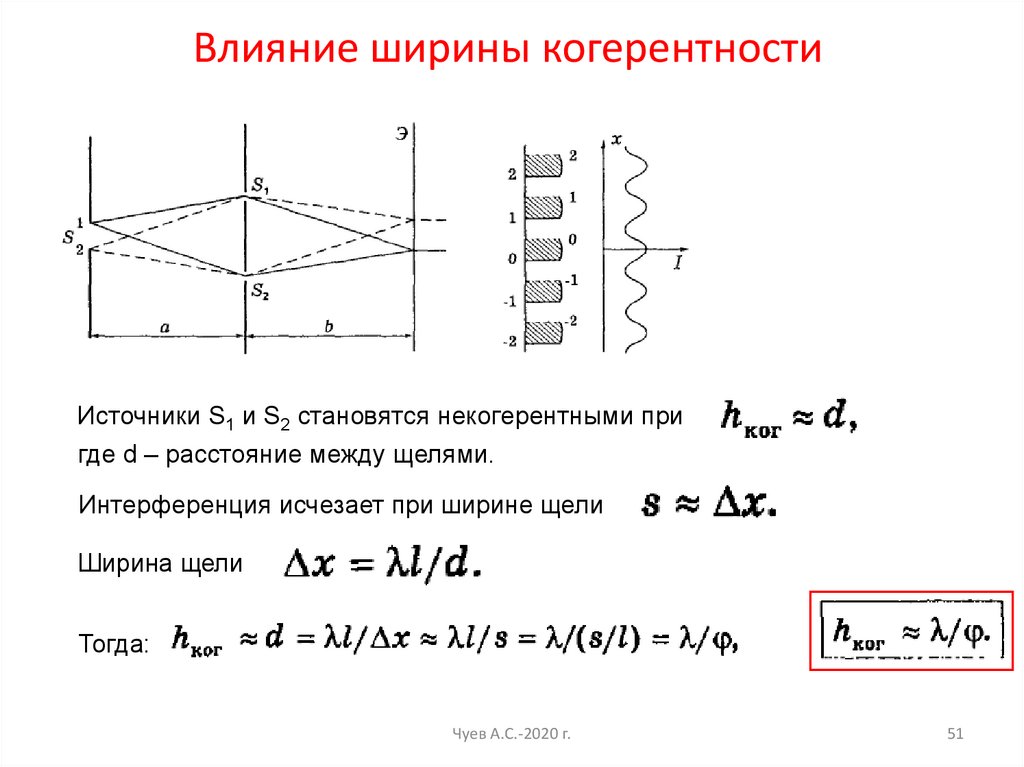
Влияние ширины когерентностиИсточники S1 и S2 становятся некогерентными при
где d – расстояние между щелями.
Интерференция исчезает при ширине щели
Ширина щели
Тогда:
Чуев А.С.-2020 г.
51
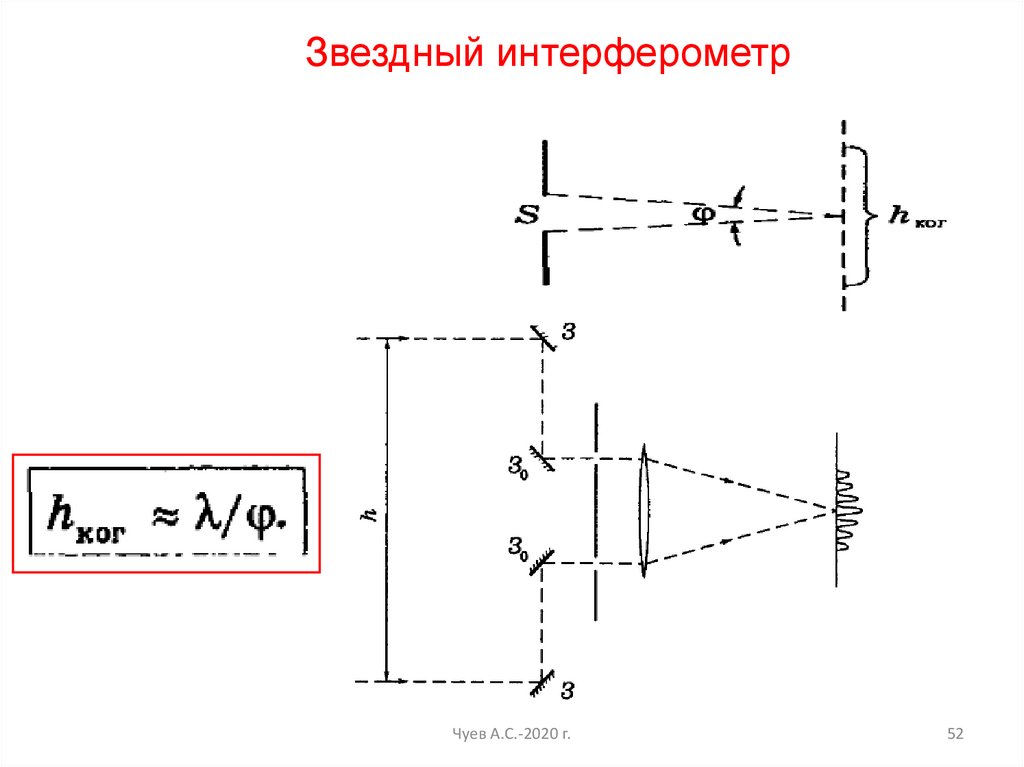
52.
Звездный интерферометрЧуев А.С.-2020 г.
52
53.
Общие выводы: интерференционная картина устойчива еслиНа практике:
Чуев А.С.-2020 г.
53
54. Конец лекции 12
Чуев А.С.-2020 г.54
55. Лекция 13
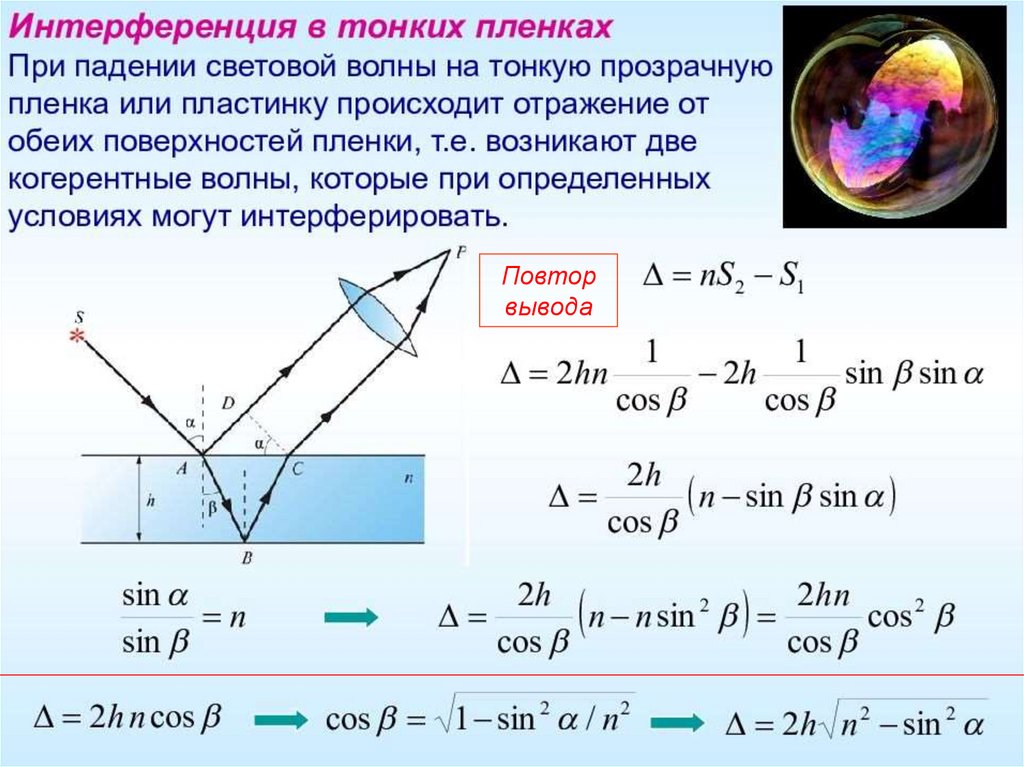
1. Интерференция света в тонкихпленках.
2. Интерференционные полосы равной
толщины и равного наклона.
3. Применение интерференции.
Чуев А.С.-2020 г.
55
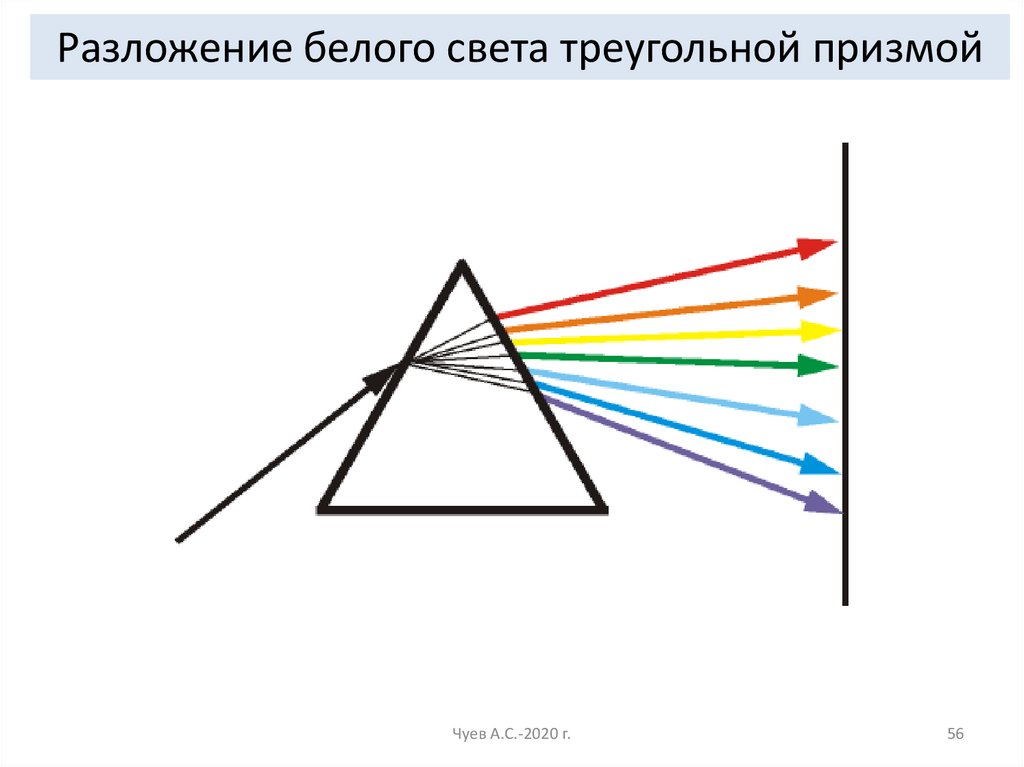
56.
Разложение белого света треугольной призмойЧуев А.С.-2020 г.
56
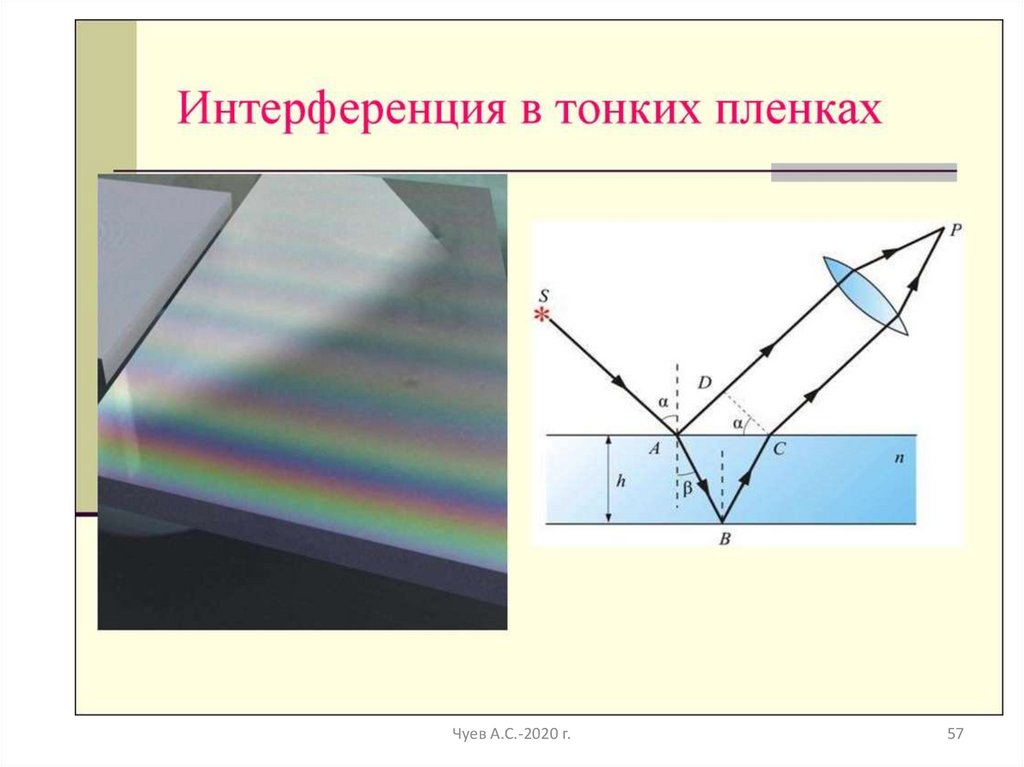
57.
Чуев А.С.-2020 г.57
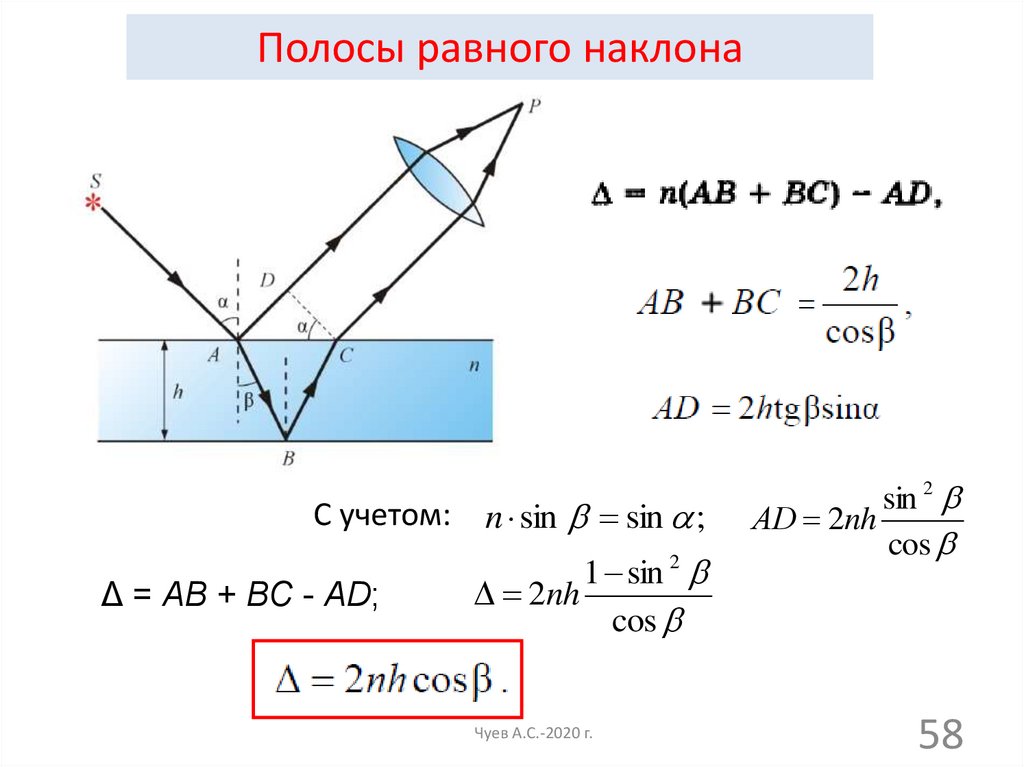
58.
Полосы равного наклонаС учетом: n sin sin ;
Δ = АВ + ВС - АD;
1 sin 2
2nh
cos
Чуев А.С.-2020 г.
sin 2
АD 2nh
cos
58
59.
С учетом потери верхним лучом полволны при отражениисвета от оптически более плотной среды, оптическая
разность хода составит:
2nh cos
2
Интерференционный максимум будет наблюдаться при:
(m 0, 1, 2, ...)
2nh cos m
2
Интерференционный минимум будет наблюдаться при:
2nh cos m
Чуев А.С.-2020 г.
(m 0, 1, 2, ...)
59
60.
С учетомn sin sin ;
формулу
2nh cos
2
можно преобразовать, представив в виде:
Для интерференции:
lког / 2;
2h lког / 2;
2
h
4
Название полосы равного наклона – т.к. интерференционные
полосы создаются плоскими волнами, падающими на пластину
под одним углом
Чуев А.С.-2020 г.
60
61.
Повторвывода
Чуев А.С.-2020 г.
61
62.
Будет рассмотрен отдельноЧуев А.С.-2020 г.
62
63.
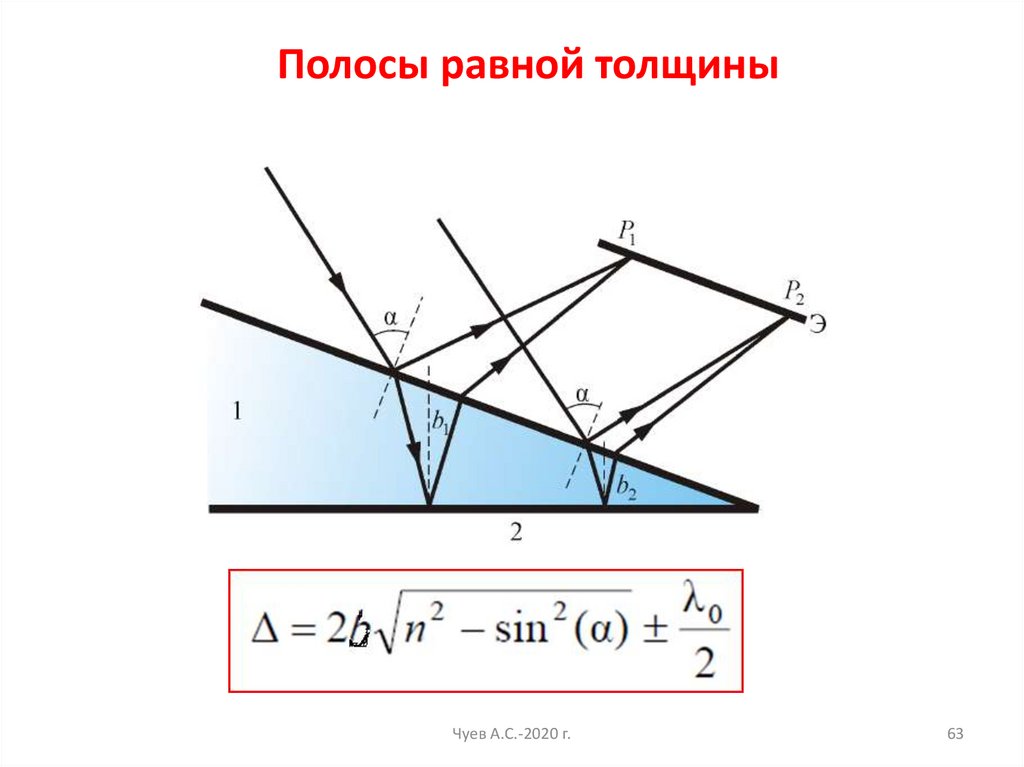
Полосы равной толщиныЧуев А.С.-2020 г.
63
64.
Чуев А.С.-2020 г.64
65.
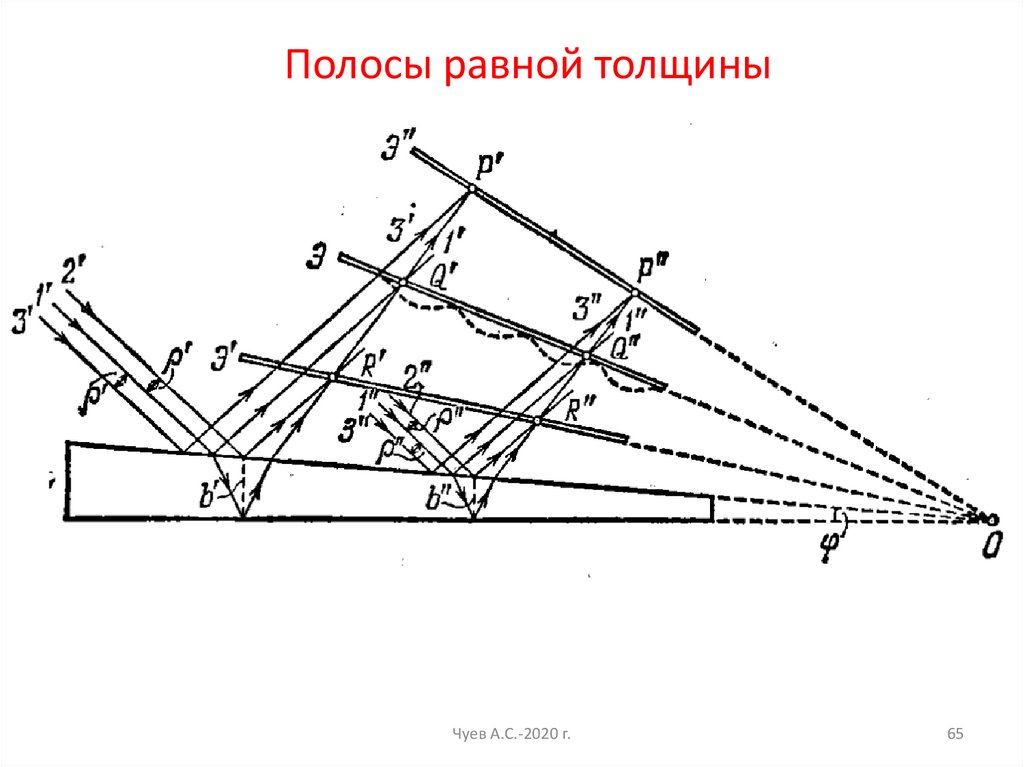
Полосы равной толщиныЧуев А.С.-2020 г.
65
66.
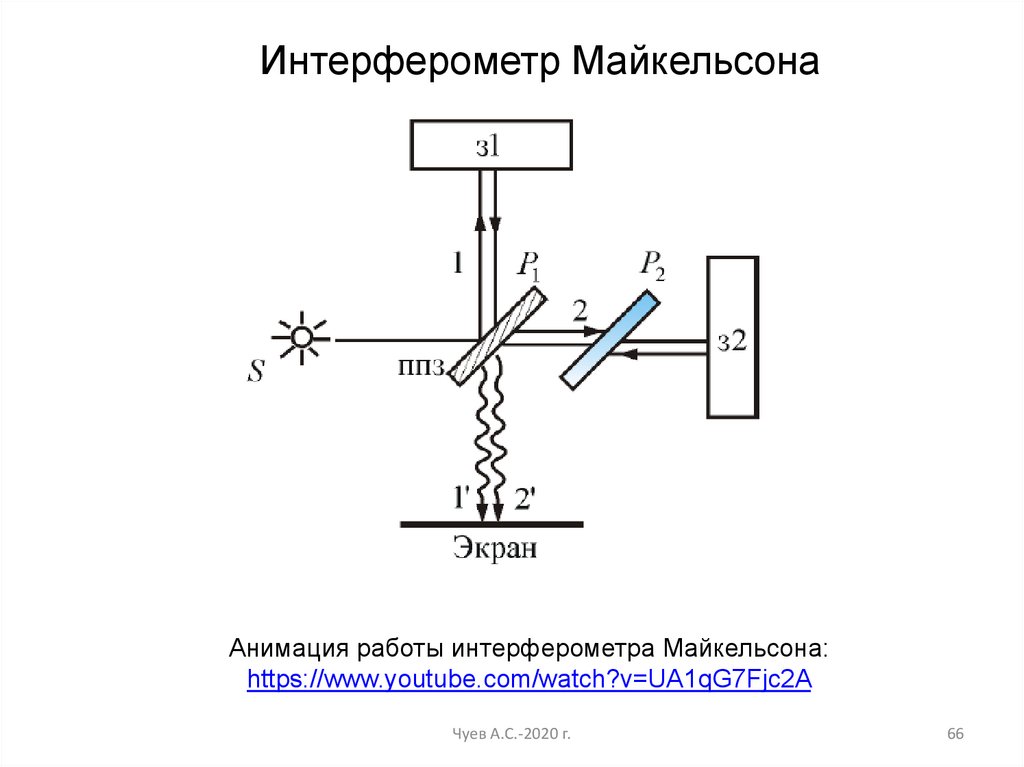
Интерферометр МайкельсонаАнимация работы интерферометра Майкельсона:
https://www.youtube.com/watch?v=UA1qG7Fjc2A
Чуев А.С.-2020 г.
66
67. Кольца Ньютона
Чуев А.С.-2020 г.67
68.
Чуев А.С.-2020 г.68
69.
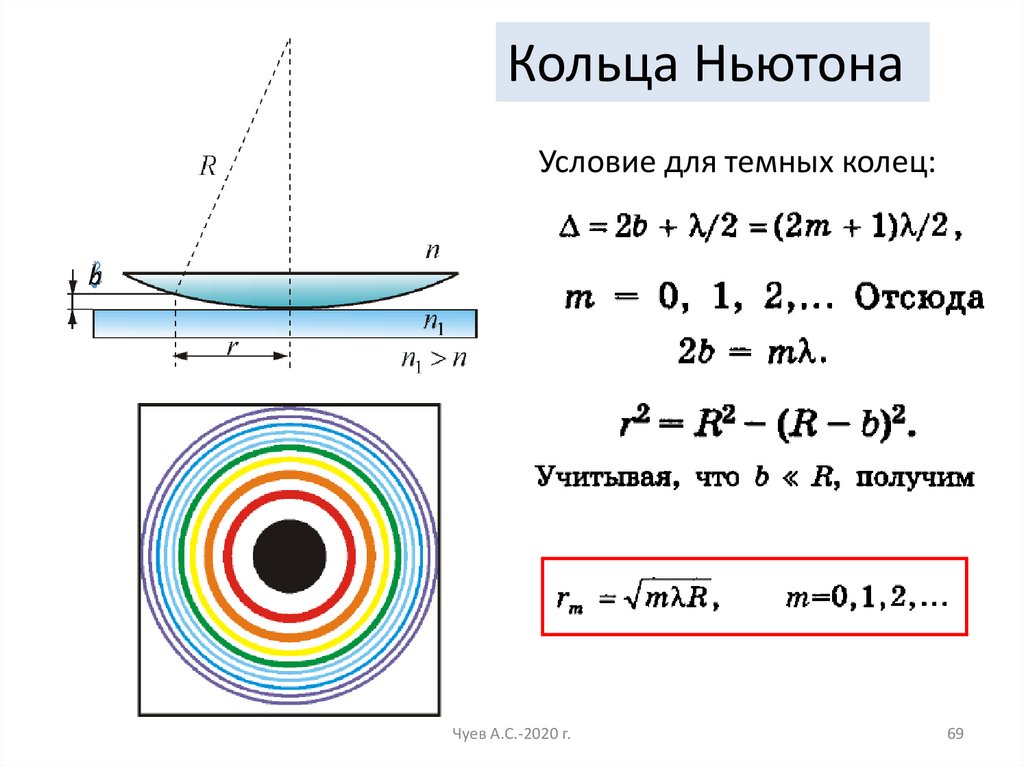
Кольца НьютонаУсловие для темных колец:
b
Чуев А.С.-2020 г.
69
70.
Задача из Иродова: Волновые процессы. Осн. законыЧуев А.С.-2020 г.
70
71.
Задача из Иродова. Определить радиус линзы, если известнырадиусы колец
Чуев А.С.-2020 г.
71
72.
Влияние зазора на радиус колецУсловие без зазора:
Оптическая разность хода лучей: 2(b b)
2
Для темных колец: 2(b b) (2m 1)
2
2
Отсюда: (b b) m
2
Радиус колец при зазоре b : r 2bR 2 R(m
Чуев А.С.-2020 г.
2
b)
72
73.
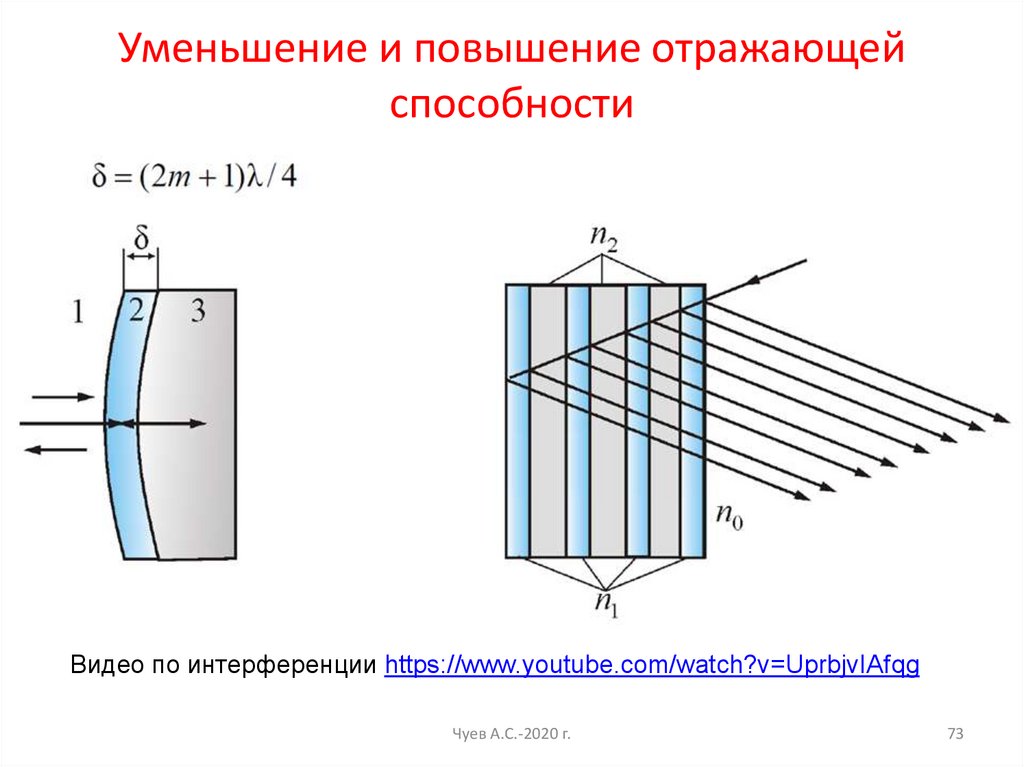
Уменьшение и повышение отражающейспособности
Видео по интерференции https://www.youtube.com/watch?v=UprbjvIAfqg
Чуев А.С.-2020 г.
73
74.
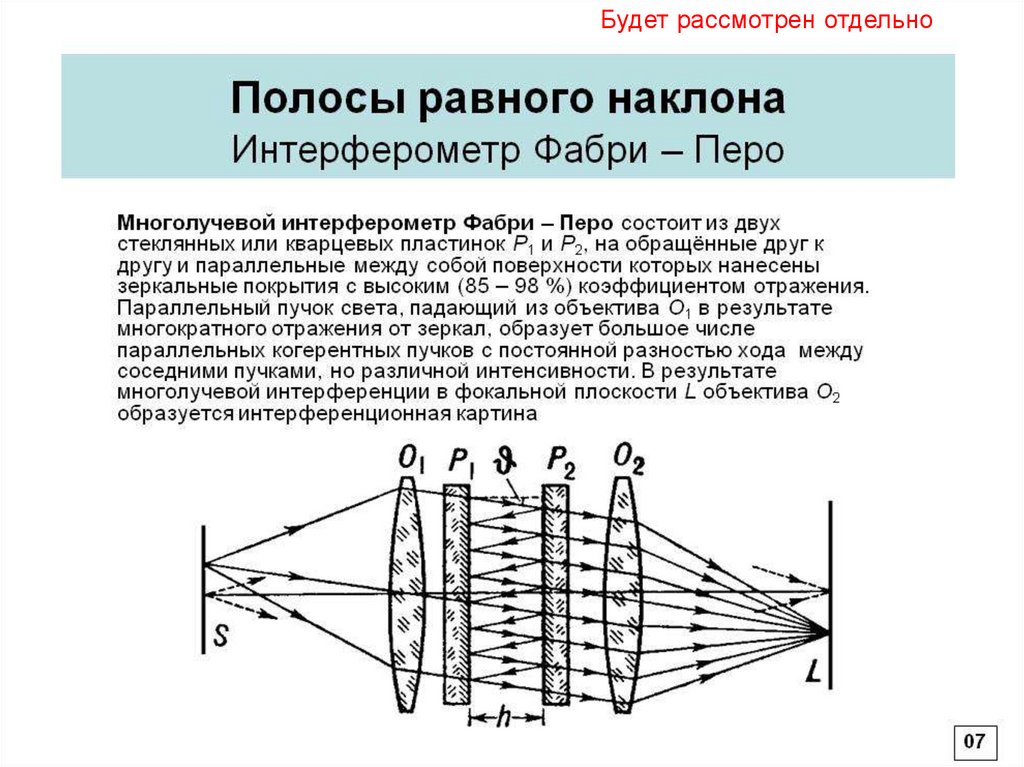
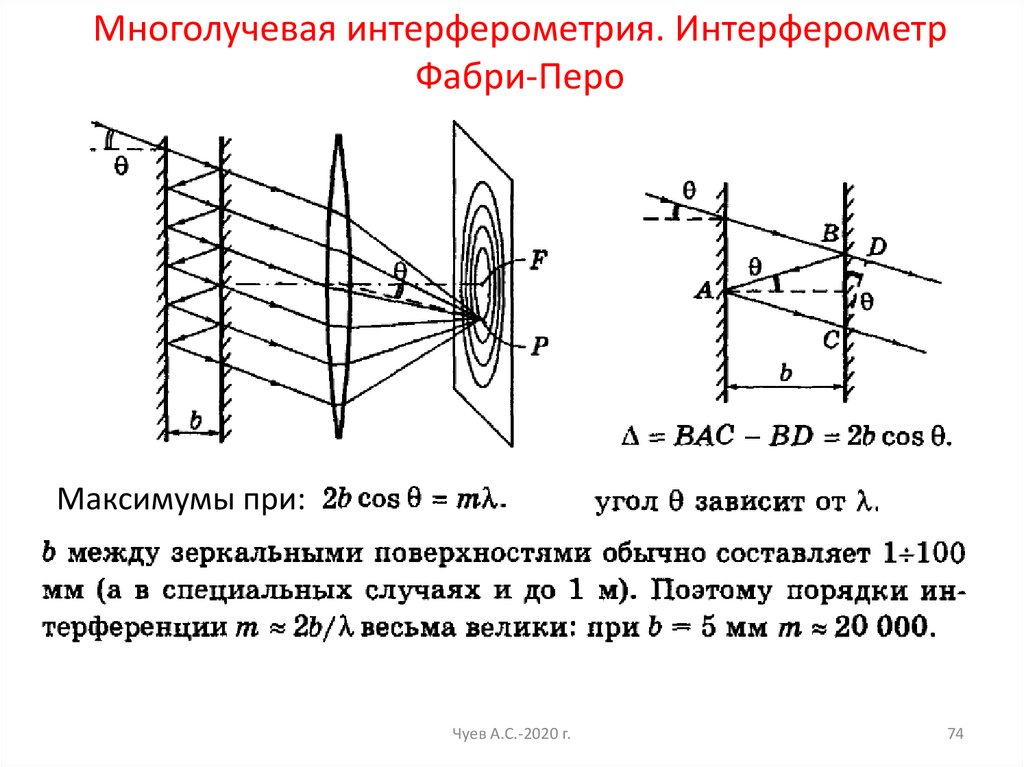
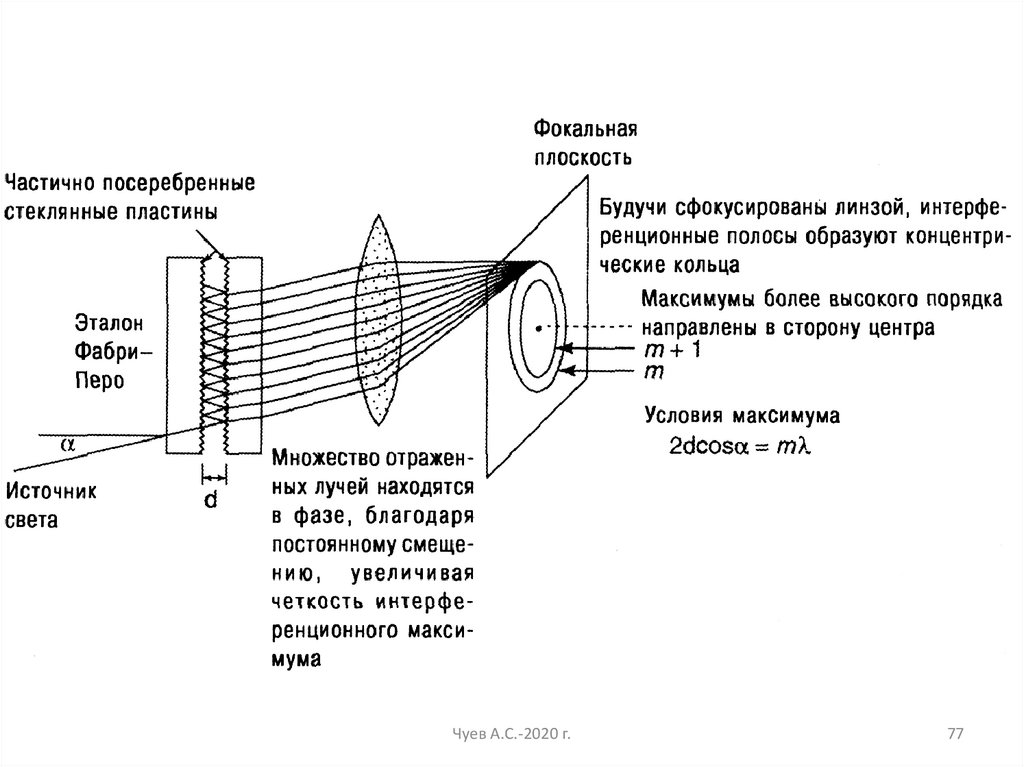
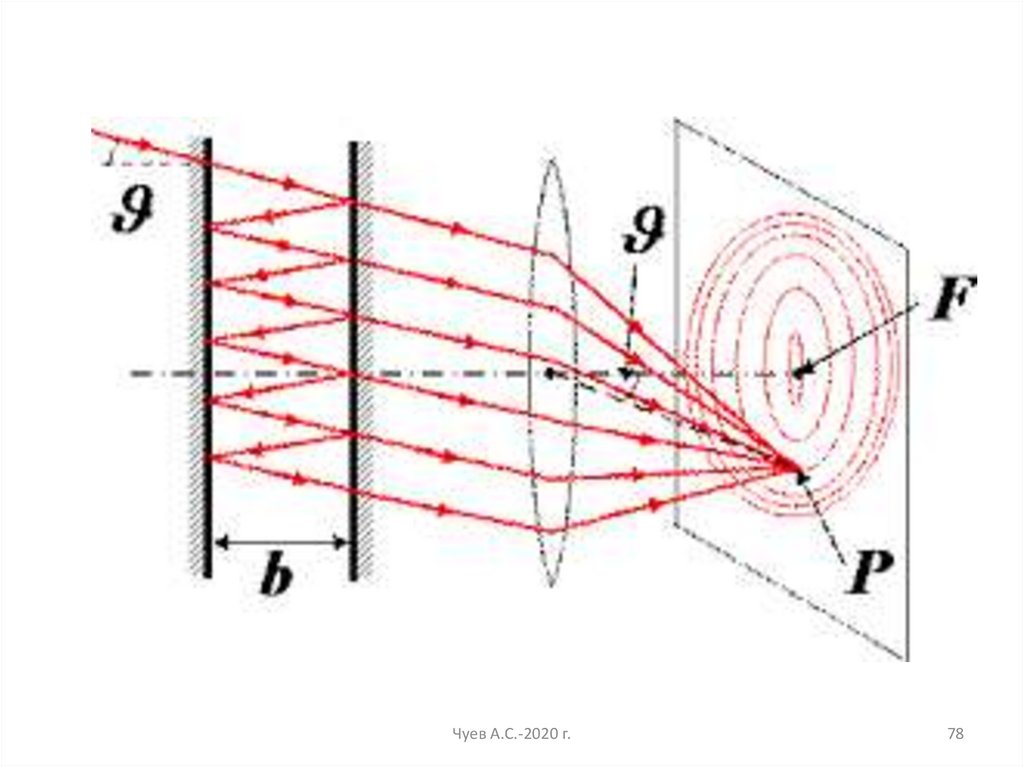
Многолучевая интерферометрия. ИнтерферометрФабри-Перо
Максимумы при:
Чуев А.С.-2020 г.
74
75.
Угловая дисперсия интерферометра Ф-П:Из
Чуев А.С.-2020 г.
75
76.
То есть, мы хорошо различаем волны только в очень узком диапазоне.Чуев А.С.-2020 г.
76
77.
Чуев А.С.-2020 г.77
78.
Чуев А.С.-2020 г.78
79.
Чуев А.С.-2020 г.79
80.
Чуев А.С.-2020 г.80
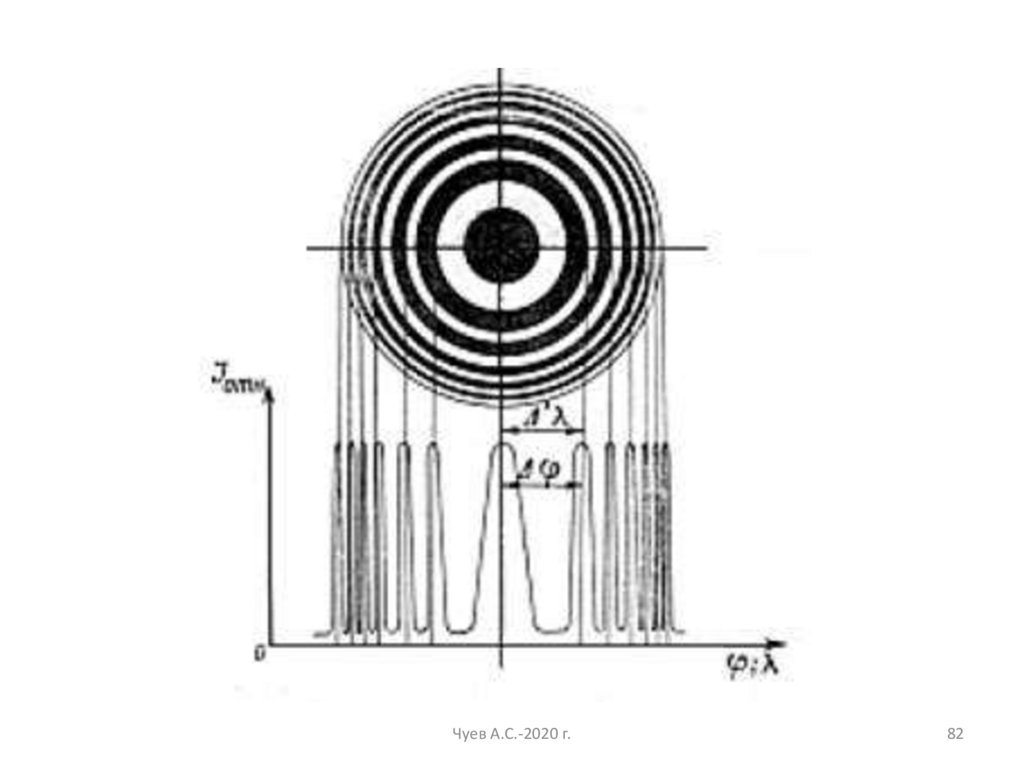
81.
Чуев А.С.-2020 г.81
82.
Чуев А.С.-2020 г.82
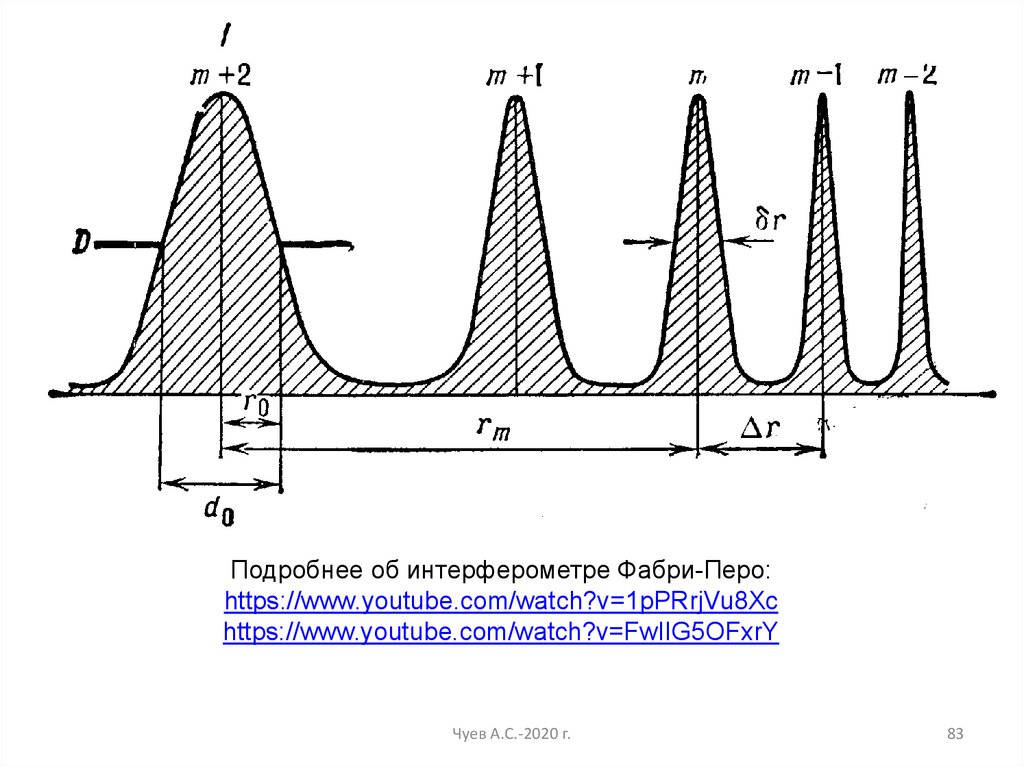
83.
Подробнее об интерферометре Фабри-Перо:https://www.youtube.com/watch?v=1pPRrjVu8Xc
https://www.youtube.com/watch?v=FwIlG5OFxrY
Чуев А.С.-2020 г.
83
84. Интерферометр Маха-Цандера
• https://www.youtube.com/watch?v=YEf6suQgEfwЧуев А.С.-2020 г.
84
85.
Принцип ФермаЧуев А.С.-2020 г.
85
86.
Конец лекции 13Чуев А.С.-2020 г.
86












































 Физика
Физика








