Аналитическая механика. Обобщенные координаты. Уравнения связей. Возможные перемещения

1.

Лекция 13. Аналитическая механика.
Обобщенные координаты. Уравнения
связей. Возможные перемещения.
Идеальные связи. Принцип возможных
перемещений. Примеры использования
принципа возможных перемещений при
определении реакций связей.
Рекомендуемая литература
1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с.
2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.
3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.
.

2.

Лекция 13
■
Аналитическая механика – устанавливает общие, единые методы изучения движения и
равновесия любых самых сложных материальных систем средствами математического
анализа. Для этого вводятся новые понятия и обобщаются старые.
■
Связи – рассматриваются теперь как некоторые условия, налагаемые на систему, которые
должны удовлетворяться в процессе движения системы. Они содержат соотношения (уравнения
или неравенства) между координатами, компонентами скоростей и ускорений и, возможно,
времени.
Классификация связей: По интегрируемости:
Голономные (геометрические) – выражаются конечными уравнениями относительно
координат или интегрируемыми дифференциальными уравнениями относительно координат:
( xk , yk , zk , t ) 0
Неголономные (кинематические) - выражаются неинтегрируемыми дифференциальными
уравнениями относительно координат,
т.е. уравнениями, содержащими не только координаты точек системы, но и их производные по
времени:
( xk , yk , zk , x k , y k , z k , t ) 0
Неинтегрируемость состоит в том, что их нельзя привести к виду уравнений голономной связи.
По зависимости от времени:
Склерономные (стационарные) – не зависящие от времени:
Например, уравнение траектории, полученное для некоторой точки шатуна кривошипношатунного механизма:
( xk , yk , zk )
рассматривается как уравнение cклерономной голономной связи:
x2
y2
a
2
b
2
0
1

3.

Если на систему N точек в пространстве наложено m
голономных связей, то декартовые координаты всегда могут
быть выражены конечными соотношениями:
Реономные (нестационарные) – зависящие от времени. Например, кинематическое
возбуждение колебаний.
x1 x1 (q1, q2 ,..., qn , t );
По освобождаемости:
Число обобщенных координат
x2 x2 (q1, q2 ,..., qn , t );
равно n =
3N – m.
Неосвобождающие (удерживающие или двухсторонние) – описываются
уравнением,
..................................;
исключающим возможность покидания точкой траектории
xN xN (q1Этому
, q2 ,...,соответствует,
qn , t ).
или поверхности, описываемой уравнением.
например, жесткая связь в
виде шарнирного стержня.
Также по у и z , где i 1, n
i
i
■
Обобщенные координаты – независимые параметры, однозначно определяющее
положение механической системы при ее движении. Обобщенность состоит в том, что они
могут иметь различную природу (линейные или угловые перемещения относительно
некоторого начального положения или какие-либо другие величины). Общее обозначение –
qi (i = 1,…,n).
■
Число степеней свободы – число независимых обобщенных координат, через которые
можно выразить декартовые координаты всех точек системы. Например:
Здесь положение любой точки стержня (например, А) однозначно определяется значением
всего одной величины – угла , который является обобщенной координатой (q = ). Число
степеней свободы равно n = 1.
2
2
2
Уравнение связи для рассматриваемой точки A:
x y l
y
xA
x A l cos ;
A
l
O
yA
y A l sin
x

4.

Лекция 13 (продолжение – 13.2)
■
Возможные перемещения – бесконечно малые перемещения, допускаемые наложенными
на систему связями (при фиксированном времени).
С точностью до бесконечно малых приращения радиуса-вектора лежат в касательной
плоскости к поверхности связи и представляют собой возможные перемещения. В случае
нестационарной голономной связи f(x,y,z,t) = 0 возможные перемещения r
рассматриваются для положения и формы поверхности связи, соответствующих данному
моменту времени. Возможные перемещения не зависят от приложенных к системе сил.
r
r
f ( x, y , z ) 0
s
s
T
■
Действительные перемещения – бесконечно малые
(элементарные) перемещения dr , действительно (фактически)
происходящие за время dt, допускаемые наложенными на
систему связями. Действительные перемещения зависят от
сил, приложенных к системе, от вида связей (стационарных,
нестационарных, голономных, неголономных) и начальных
условий. Таким образом, возможные перемещения являются более
общим понятием, чем действительные перемещения.
Поскольку вектор положения точки системы можно выразить через
обобщенные координаты
,
то возможные перемещения выражаются через приращения
обобщенных координат как полный дифференциал:
r
r
r
rk k q1 k q2 ... k qn
q1
q2
qn
n
или
rk
i 1
k 1,..., N
rk
qi .
qi

5.

■
Вычисление возможных перемещений:
Геометрический способ - в силу малости возможных перемещений при повороте твердого
тела любая его точка может рассматриваться движущейся не по дуге, а по
перпендикуляру к радиусу вращения в сторону угла поворота:
x A l l cos ; Для малых углов cos ≈ 1, sin ≈ , тогда: x A 0;
y A l sin .
y A s A l .
xA
O
l
A
x
yA= sA
Например, для наклонного стержня:
sA
y
A
l
O
x
s A l .
x A s A sin l sin ;
y A s A cos l cos .

6.

Аналитический способ – вычисляется вариация от координат:
y
xA
l
O
A
x A l cos ;
yA
y A l sin
x
(l cos ) l sin ;
y A
(l sin ) l cos .
x A
В отличие от геометрического способа знаки возможного
приращения координат получаются автоматически. При
использовании геометрического способа в дальнейших
вычислениях, например, работы, необходимо учитывать
направление полученного приращения (перемещения).
■
Возможная работа силы – элементарная работа силы на том или ином
возможном перемещении:
A F r .
В координатном виде:
A X x Y y Z z.
В естественном виде:
A F s cos( F , r ).

7.

Лекция 13 (продолжение – 13.3)
■
Идеальные связи – связи, при которых сумма элементарных работ сил реакций
связи на любом возможном перемещении равна нулю:
n
A R Rk rk 0.
k 1
Примеры идеальных связей: абсолютно гладкая поверхность (при скольжении), абсолютно
твердая поверхность (при качении без скольжения). Любую неидеальную связь можно
рассматривать как идеальную, если соответствующие реакции связи (совершающие
работу на возможных перемещения) причислить к задаваемым (активным) силам.
■
Принцип возможных перемещений – Для равновесия материальной системы,
подчиненной голономным, стационарным, двухсторонним и идеальным
связям, необходимо и достаточно, чтобы сумма элементарных работ всех
активных сил на любом возможном перемещении из предполагаемого
положения равновесия равнялось нулю:
n
F
Доказательство необходимости: Система находится
A Fk rk 0.
в равновесии и для каждой точки удовлетворяется
k 1
уравнение равновесия:
Умножим скалярно на вектор возможного перемещения
точки и сложим:
F r R r
k
k
k
=0
k
0.
n
A Fk rk 0.
F
k 1

8.

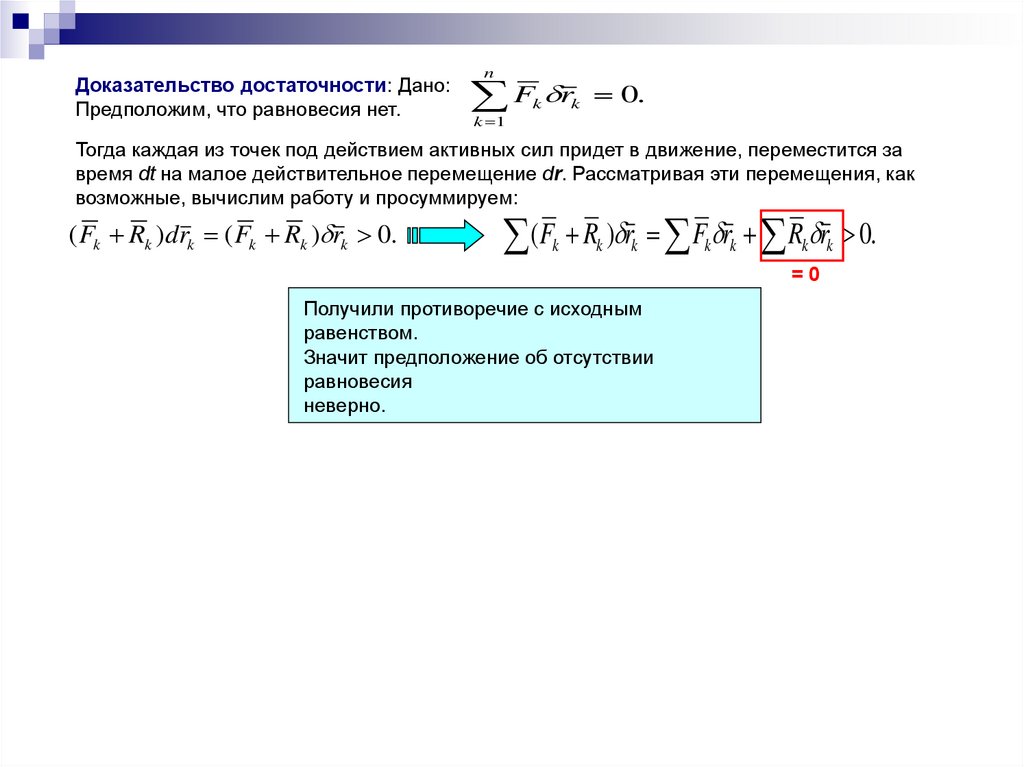
Доказательство достаточности: Дано:
Предположим, что равновесия нет.
n
F r
k 1
k
k
0.
Тогда каждая из точек под действием активных сил придет в движение, переместится за
время dt на малое действительное перемещение dr. Рассматривая эти перемещения, как
возможные, вычислим работу и просуммируем:
( Fk Rk )drk ( Fk Rk ) rk 0.
(F R ) r F r R r 0.
k
k
k
k
k
k
=0
Получили противоречие с исходным
равенством.
Значит предположение об отсутствии
равновесия
неверно.
k

9.

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР С ПОМОЩЬЮ
ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ.
■
Примеры использования принципа возможных перемещений для определения
реакций связей:
Пример 1. Определить реакцию балки в правой опоре:
P
A
RB
B
sP
a
l
sB
Балка неподвижна и не имеет ни возможных, ни действительных
перемещений. Отбросим связь, реакция
которой отыскивается, и заменим ее реакцией:
Без правой опоры балка может поворачиваться под действием
активных сил, реакцию RB причисляем к активным силам. Зададим
малое возможное перемещение:
Вычислим возможные перемещения: sP a ; sB l .
Запишем сумму работ:
AP R P sP RB sB 0.
Pa RBl 0.
RB
Pa Pa
.
l
l

10.

Пример 2. Определить опорный момент многопролетной составной балке в левой опоре:
Отбросим в жесткой заделке связь, препятствующую повороту балки, и заменим ее парой
сил MA:
Вычислим возможные перемещения:
A
F
M
D
C
B
E
A
sD
sB
b
l
b
a
l
s B l ;
s D s B l ;
s F
Запишем сумму работ:
A M A F sF 0.
M A F
a
l 0.
l a
M A F
a
l.
l a
a
a
s D
l .
l a
l a
Заметим, что
1. для нахождения опорного момента MA
из уравнений статики потребовалось бы решить как
минимум три уравнения равновесия;
2. эпюра возможных перемещений пропорциональна
линии влияния усилия;
3. если задать возможное перемещение для искомой
реакции равным 1, например, =1, то эпюра
перемещений будет полностью тождественна линии
влияния поскольку
A M A 1 1 s F ( z) 0; M A s F ( z).

11.

ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР С ПОМОЩЬЮ
ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Пример 4. На составную балку АВ
действует распределенная нагрузка
интенсивности q = 2 кН/м, наклонная
сила F = 4 кН и пара сил с моментом М =
5 кН м. а = 2 м.
Наложены связи: в точке В – неподвижная шарнирная опора,
в точке Е – горизонтальная скользящая заделка.
О п р е д е л и т ь: XВ, УВ, УЕ, МЕ.
Примечание. Скользящая заделка - это заделка, которая
«запрещает» поворот, но не ограничивает
поступательное перемещение вдоль направляющих, по
которым заделка
может скользить. Реакции скользящей
заделки: RA реакция, перпендикулярная
направляющим, и реактивный момент – МА.

12.

А) Определим горизонтальную реакцию в шарнире В
1. Заменим неподвижный шарнир В
подвижным шарниром и реакцией X В .
2. Сообщим балке АВ возможное
перемещение.
rC rC
r C rC rCrC r C rC
rВ
rВ
Часть балки АС может поступательно перемещаться влево
или вправо по горизонтали на rС . Обозначим | rC | s.
Шарнир В может перемещаться влево или вправо на rB .
Перемещения rС и rВ направлены
по соответствующим
возможным скоростям VС и VВ . М.ц.с. для ВС лежит в .
Т.е. VС VВ V и rС rВ r . Или | rС | | rВ | | r | s.
Возможное перемещение балки будет поступательным на s.
3. Сумма возможных работ всех сил и пар сил, действующих
на балку, по принципу Лагранжа должна быть равна нулю.
ΣδАk = XВ δs + F cos (600) δs = 0,

13.

Поделим уравнение (1) на δs ≠ 0 и получим
XВ + F cos (600) = 0.
Откуда находим XВ = – F cos (600) = – F / 2 = – 2 (кН).
Знак минус указывает на то, что реакция направлена влево.
В) Определим вертикальную реакцию в шарнире В.
1. Заменим неподвижный шарнир В
подвижным шарниром и реакцией У В .
2. Сообщим балке АВ возможное
перемещение.
Часть балки АС может перемещаться
только поступательно влево или
вправо, так как в точке Е скользящая
заделка.
r C rC r C rC rCrC r C rC

14.

Шарнир В может перемещаться
только
(| rB | sB ).
вертикально на rB ,
δφ
rC
rC
rC Р rC
rВ
rВ
М. ц. с. для части балки СВ будет в точке С.
Следовательно, | rC | s 0, т.е., связи, наложенные на
балку, у ее части АС не допускают возможных перемещений.
Часть балки ВС может поворачиваться вокруг м. ц. с. (т. С)
на угол δφ.
3. Сумма возможных работ всех сил и пар сил, действующих
на балку, по принципу Лагранжа должна быть равна нулю.
Примечание. Применим выражение
для работы силы,
ΣδАk = М δφ – F cos (300) 2 а δφ + УВ 4 а δφ = 0.
приложенной к вращающемуся телу: А = М0Z(F) · φ .
Откуда находим УВ = F cos (300) / 2 – М / (4а) = 1,12 (кН).

15.

С) Найдем момент пары сил, возникающей в скользящей
заделки, наложенной в точке Е.
1. Заменим скользящую заделку
шарнирно подвижной опорой и
неизвестным реактивным моментом МЕ.
2. Сообщим балке АВ возможное
перемещение.
Связи допускают только поворот части балки ВС вокруг
шарнира В на угловое перемещение δφ1.
М.ц.с. для части балки АС будет в точке Е.
Обозначим угол поворота АС вокруг м. ц. c. через δφ2 .
3. Составим уравнение возможных работ (1).
ΣδА k = – М δφ1 – F cos (300) 2 а δφ1 + МЕ δφ2 + Q 3а δφ2 = 0. (3)
Выразим δφ2 через δφ1.
δsc = 4 a δφ1 = 2 a δφ2,
т. е. δφ2 = 2 δφ1.

16.

Подставляя последнее соотношение в уравнение (3) и
разделив на δφ1, получим:
– М – F cos (300) 2 а + 2 МЕ + Q 3 а 2 = 0,
Откуда найдем: МЕ =М / 2 + F cos (300) а – Q 3а = – 38,57 (кНм).
D) Определим вертикальную реакцию в скользящей заделке,
наложенной на точку Е балки.
1. Заменим скользящую заделку
двойной скользящей заделкой,
и
вертикальной реакцией У Е .
Двойная скользящая заделка – связь которая допускает любое
2.
Сообщим балке
АВ возможное
поступательное
перемещение
в плоскости действия сил, но
перемещение.
исключает возможность поворота.
Часть балки ВС может повернуться вокруг шарнира В.
Обозначим это угловое перемещение δφ.
Тогда другая часть балки АС переместится поступательно на
величину δs вверх.

17.

3. Составим уравнение возможных
работ (1).
ΣδАk = – М δφ – F cos (300) 2а δφ – Q δs + УЕ δs = 0.
(4)
Учитывая, что δ s = 4а δφ, из уравнения (4) найдем
УЕ = М /4а + F cos (300) / 2 + Q = 10,36 (кН).
Е) Сделаем проверку.
Заменим все внешние опоры
их реакциями.
Используем уравнения равновесия в основной
форме:
ΣFkX = 0, ΣFkУ = 0, М С(Fκ ) 0.
ΣFkX = ХВ + F cos600 = 0,
ΣFkУ = УВ + УЕ – Q – F cos300 = 0,
(1)
(2)
М С(Fk ) = Q 5а –УЕ 2а + МЕ + М – F cos (300) 2а + УВ 4а = 0. (3)

18.

Примечание 1. В тех вариантах, где нет жесткой заделки или
скользящей заделки, уравнение (3) (ΣМС = 0) можно не
составлять.
Примечание 2. В качестве моментной точки в уравнении (3)
необходимо всегда выбирать точку С, что позволит проверить
все вертикальные реакции и реактивный момент.
Подставляя в уравнение (1) найденную реакцию ХВ , получим:
ΣFkX = XВ + F cos (600) = – 2 + 4/2 ≡ 0.
Подставляя в уравнение (2) реакции УВ и УЕ , найдем:
ΣFkУ = УВ + УЕ – Q – F cos300 = 1,12 + 10,36 – 8 – 3,48 ≡ 0.
Подставляя в уравнение (3) реакции УВ ,УЕ и момент МЕ,
найдем:
М С(Fk )= 8 .5 . 2 – 10,36 . 2 . 2 – 38,57 + 5 – 4 . 2 . 2 / 2 +1,12 . 4 .2=
= 93,96 – 93,88 = 0,08 ≈ 0.
Ответ: УВ = 1,12кН, XВ = – 2кН, УЕ =10,36кН, МЕ = – 38,57кНм.

19.

Применение принципа возможных
перемещений к простейшим системам
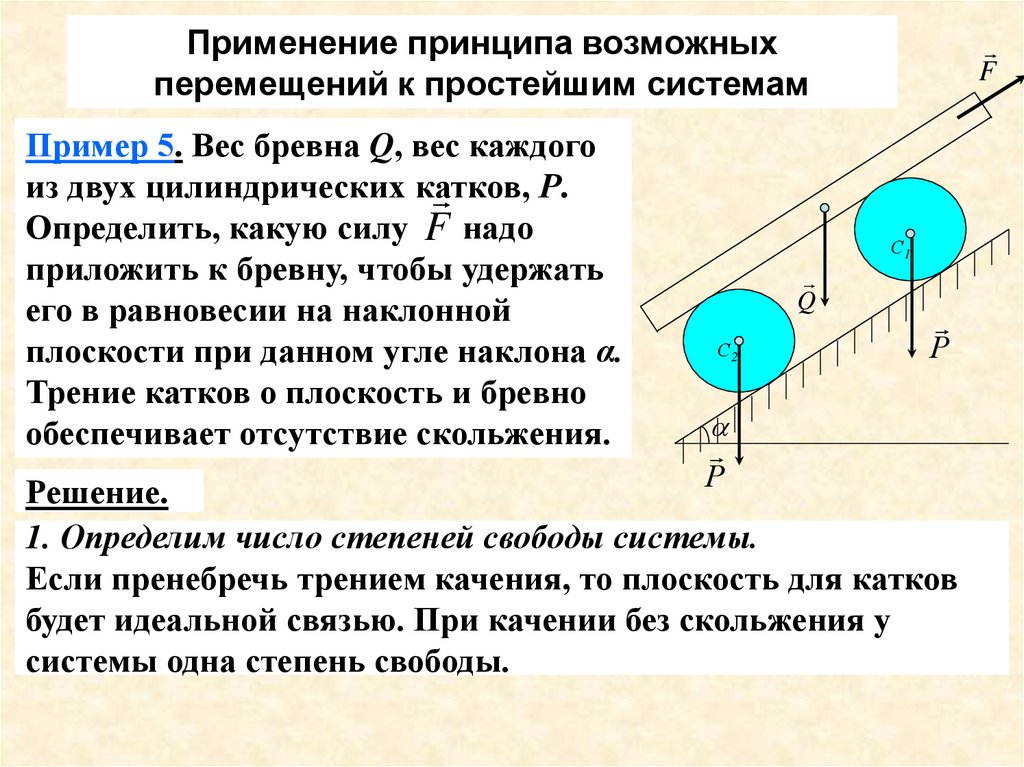
Пример 5. Вес бревна Q, вес каждого
из двух цилиндрических катков,
Р.
Определить, какую силу F надо
приложить к бревну, чтобы удержать
его в равновесии на наклонной
плоскости при данном угле наклона α.
Трение катков о плоскость и бревно
обеспечивает отсутствие скольжения.
F
С1
Q
С2
Р
Р
Решение.
1. Определим число степеней свободы системы.
Если пренебречь трением качения, то плоскость для катков
будет идеальной связью. При качении без скольжения у
системы одна степень свободы.

20.

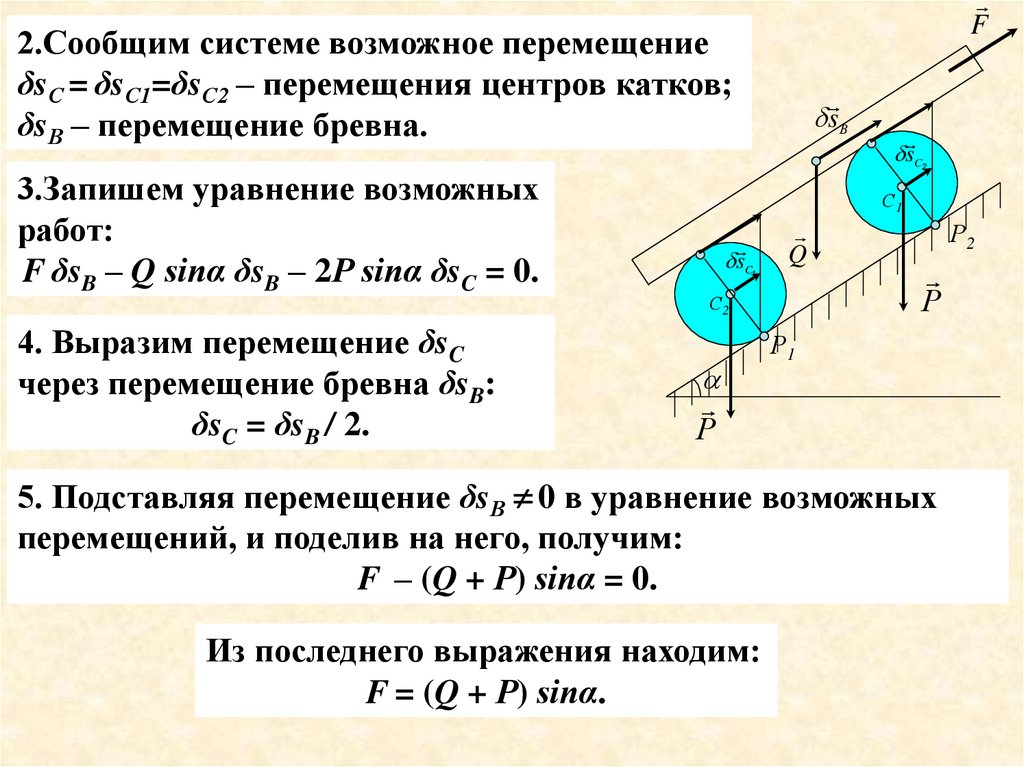
F
2.Сообщим системе возможное перемещение
δsС = δsС1=δsС2 – перемещения центров катков;
δsВ – перемещение бревна.
3.Запишем уравнение возможных
работ:
F δsB – Q sinα δsB – 2Р sinα δsC = 0.
4. Выразим перемещение δsC
через перемещение бревна δsB:
δsC = δsB / 2.
s В
sC
2
С1
sC
Q
1
С2
Р2
Р
Р1
Р
5. Подставляя перемещение δsВ 0 в уравнение возможных
перемещений, и поделив на него, получим:
F – (Q + Р) sinα = 0.
Из последнего выражения находим:
F = (Q + Р) sinα.