Похожие презентации:
Объемы тел
1.
Объемы телГеометрия, 11 класс
2. ВНИМАНИЕ!
• Сделать качественный конспект втетради, опираясь на презентацию и
учебник!
3. Понятие объема
За единицу измеренияобъемов принимают куб,
ребро которого равно
единице измерения отрезков.
Единицы измерения объемов:
мм3;см3;дм3;м3;км3.
1 литр = 1 дм3
4. Основные свойства объемов
1о. Равные теларавные объемы.
имеют
2о.Если тело составлено из
нескольких тел, то объем
равен сумме объемов этих
тел.
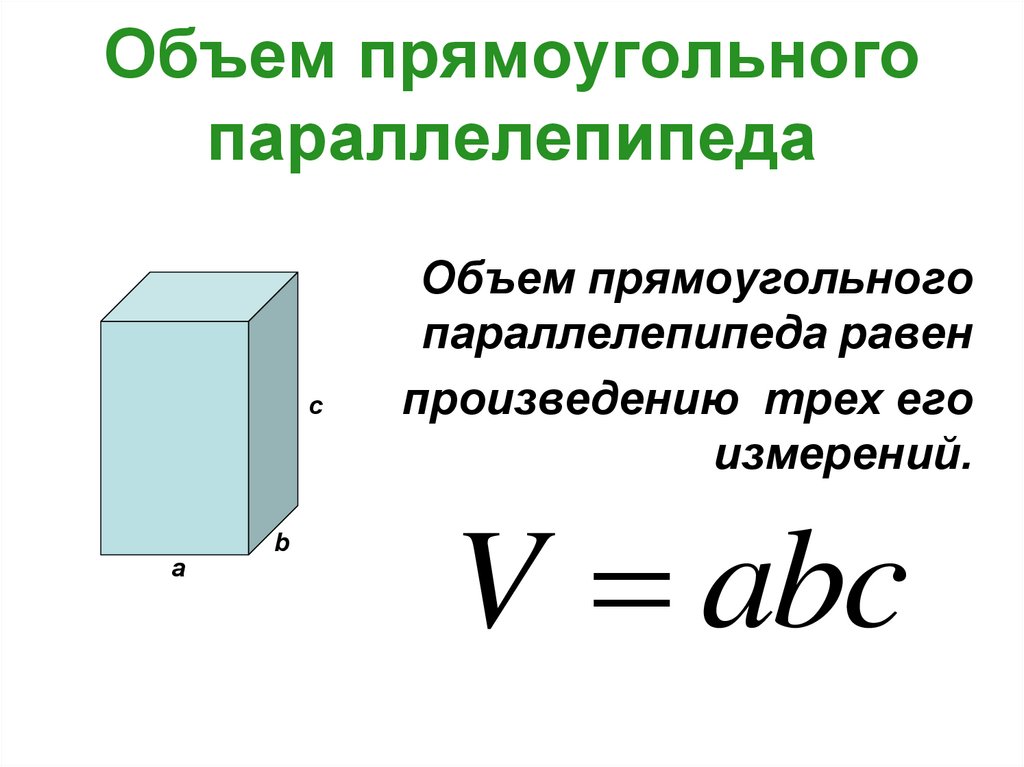
5. Объем прямоугольного параллелепипеда
cb
a
Объем прямоугольного
параллелепипеда равен
произведению трех его
измерений.
V abc
6. Следствие 1
Sоснh
Объем прямоугольного
параллелепипеда
равен произведению
основания на высоту.
V Sосн h
7. Следствие 2
Объем прямой призмы,основанием которой является
прямоугольный треугольник,
равен произведению
основания на высоту.
V Sосн h
8. Объем прямой призмы
Объем прямой призмыравен произведению
основания на высоту.
V Sосн h
9. Объем цилиндра
Объем цилиндра равенпроизведению
основания на высоту.
V Sосн h
V R h
2
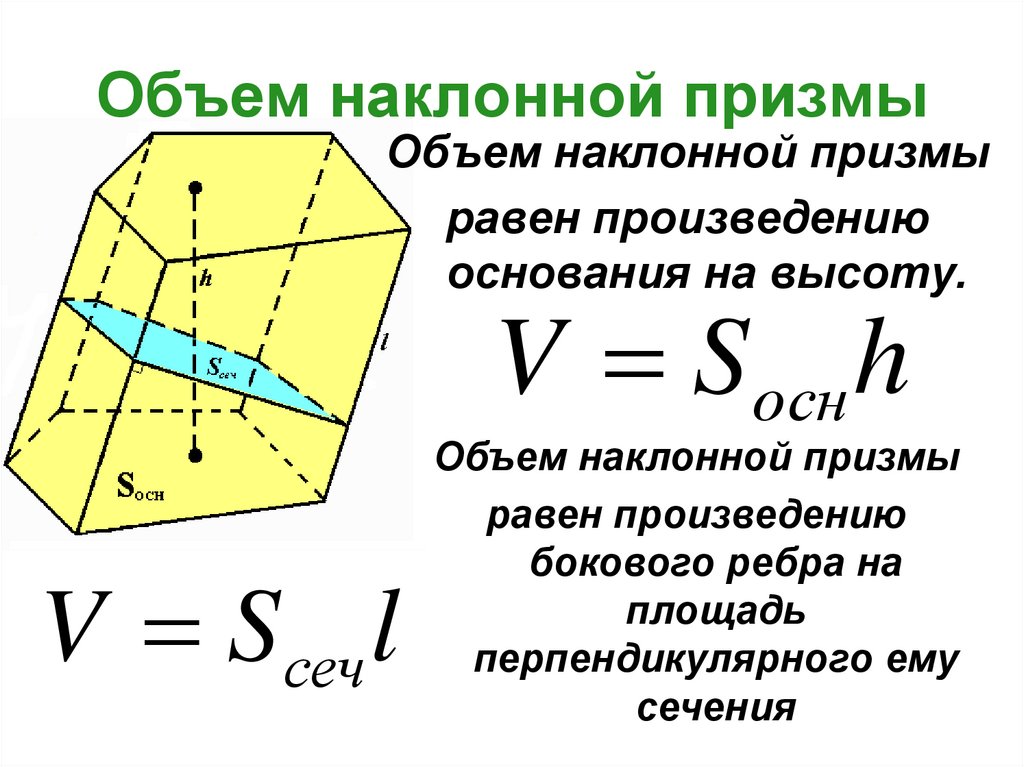
10. Объем наклонной призмы
Объем наклонной призмыравен произведению
основания на высоту.
V Sосн h
V Sсеч l
Объем наклонной призмы
равен произведению
бокового ребра на
площадь
перпендикулярного ему
сечения
11. Объем пирамиды
Объем пирамиды равенодной трети произведения
площади основания на
высоту.
1
V S осн h
3
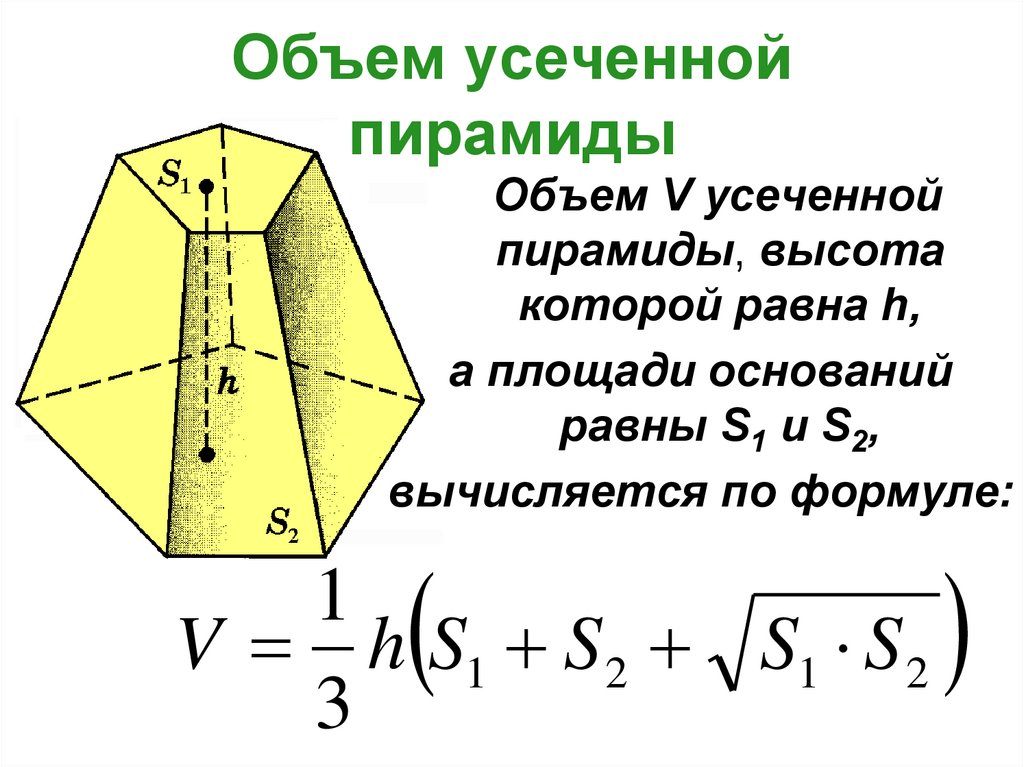
12. Объем усеченной пирамиды
Объем V усеченнойпирамиды, высота
которой равна h,
а площади оснований
равны S1 и S2,
вычисляется по формуле:
1
V h S1 S 2 S1 S 2
3
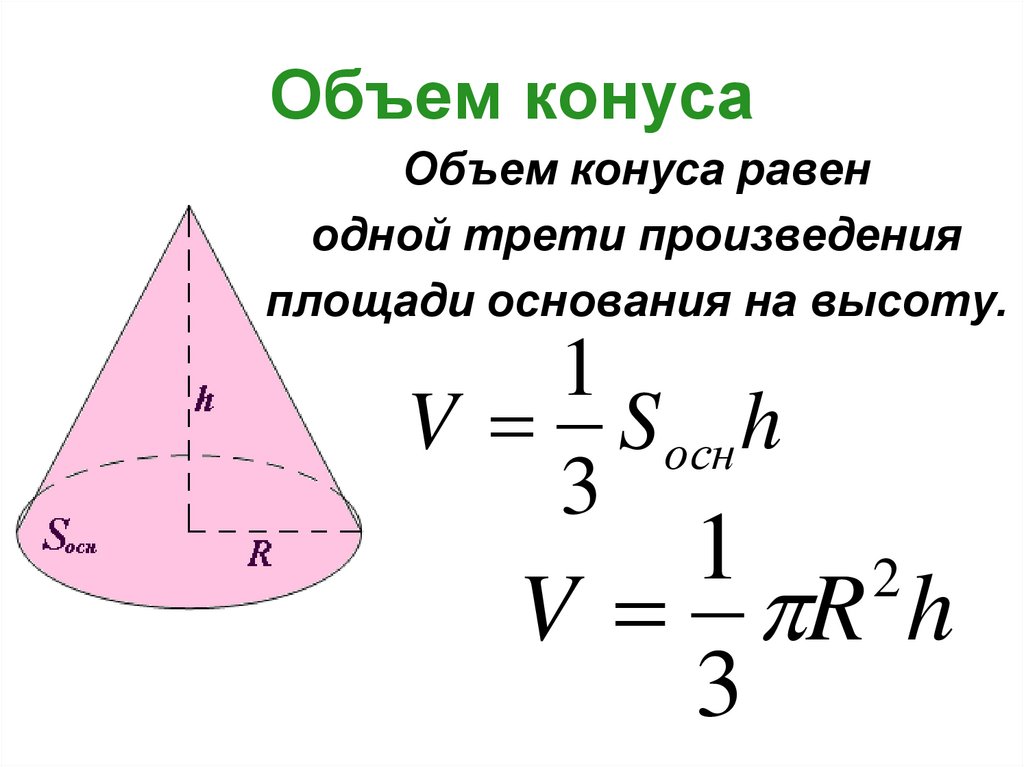
13. Объем конуса
Объем конуса равенодной трети произведения
площади основания на высоту.
1
V S осн h
3
1 2
V R h
3
14. Объем усеченного конуса
Объем V усеченного конуса,высота которого равна h,
а площади оснований равны S1
и S2,
вычисляется по формуле:
1
V h S1 S 2 S1 S 2
3
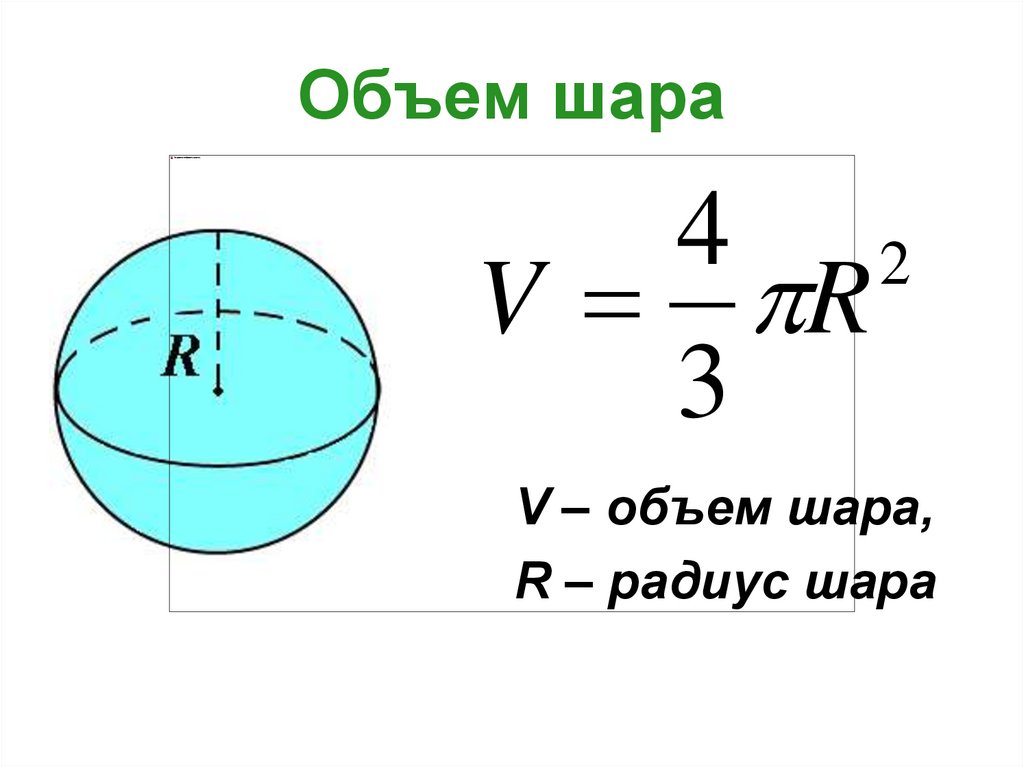
15. Объем шара
4 2V R
3
V – объем шара,
R – радиус шара
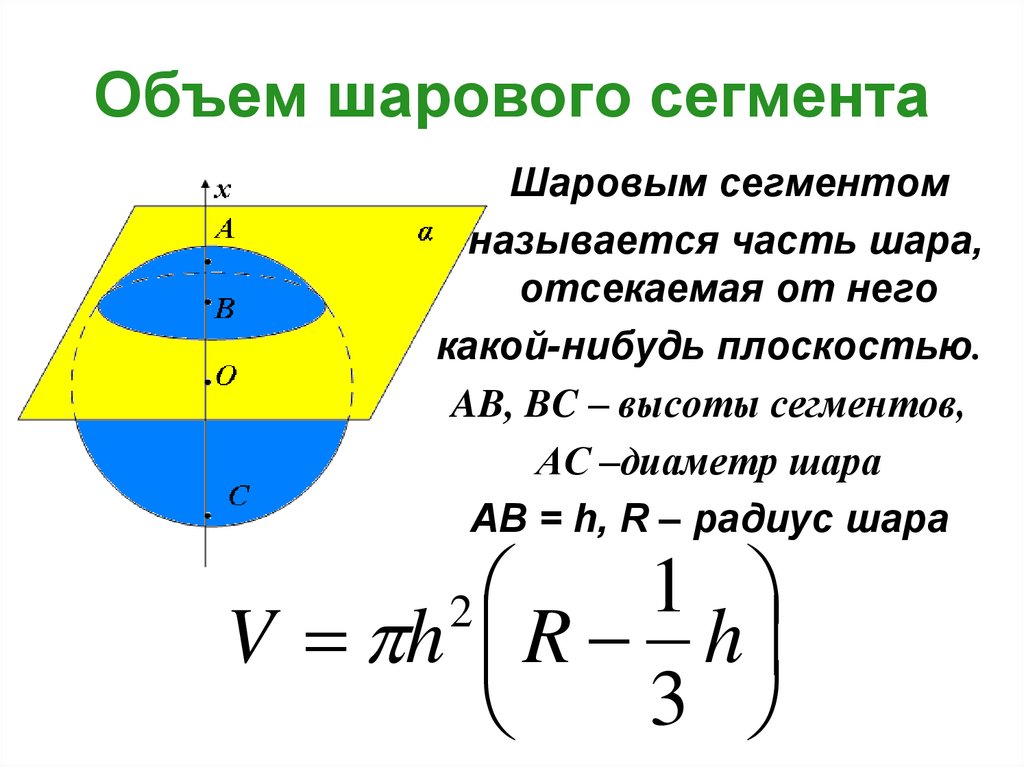
16. Объем шарового сегмента
Шаровым сегментомназывается часть шара,
отсекаемая от него
какой-нибудь плоскостью.
AB, BC – высоты сегментов,
АС –диаметр шара
AB = h, R – радиус шара
1
V h R h
3
2
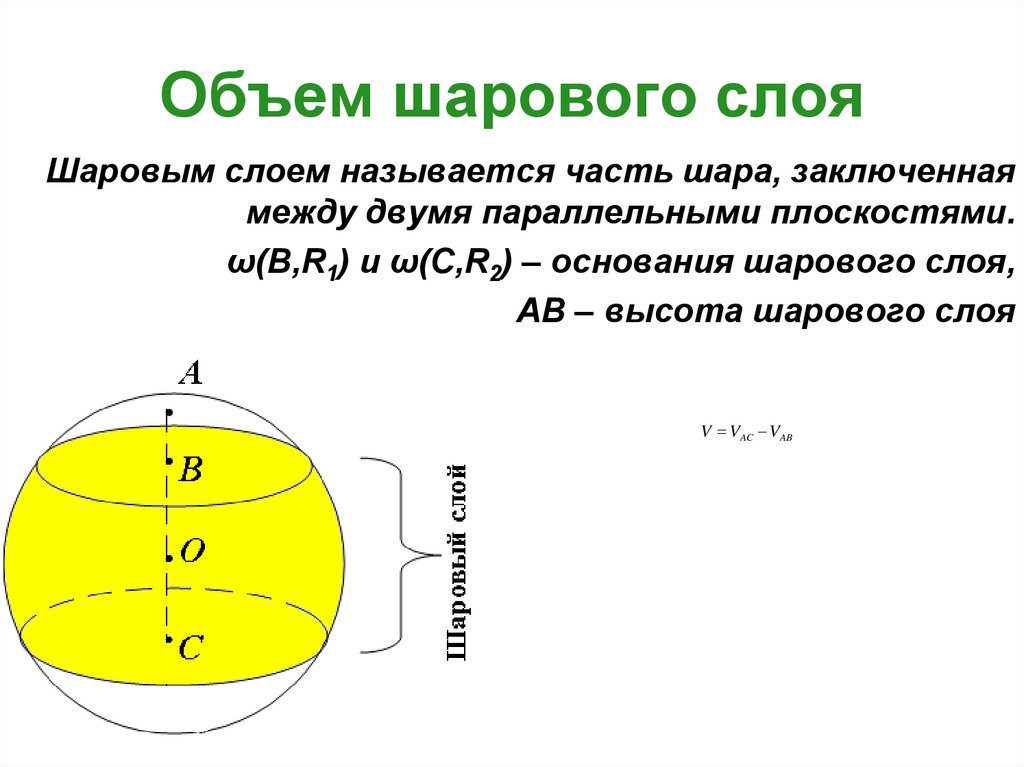
17. Объем шарового слоя
Шаровым слоем называется часть шара, заключеннаямежду двумя параллельными плоскостями.
ω(В,R1) и ω(С,R2) – основания шарового слоя,
АВ – высота шарового слоя
V VAC VAB
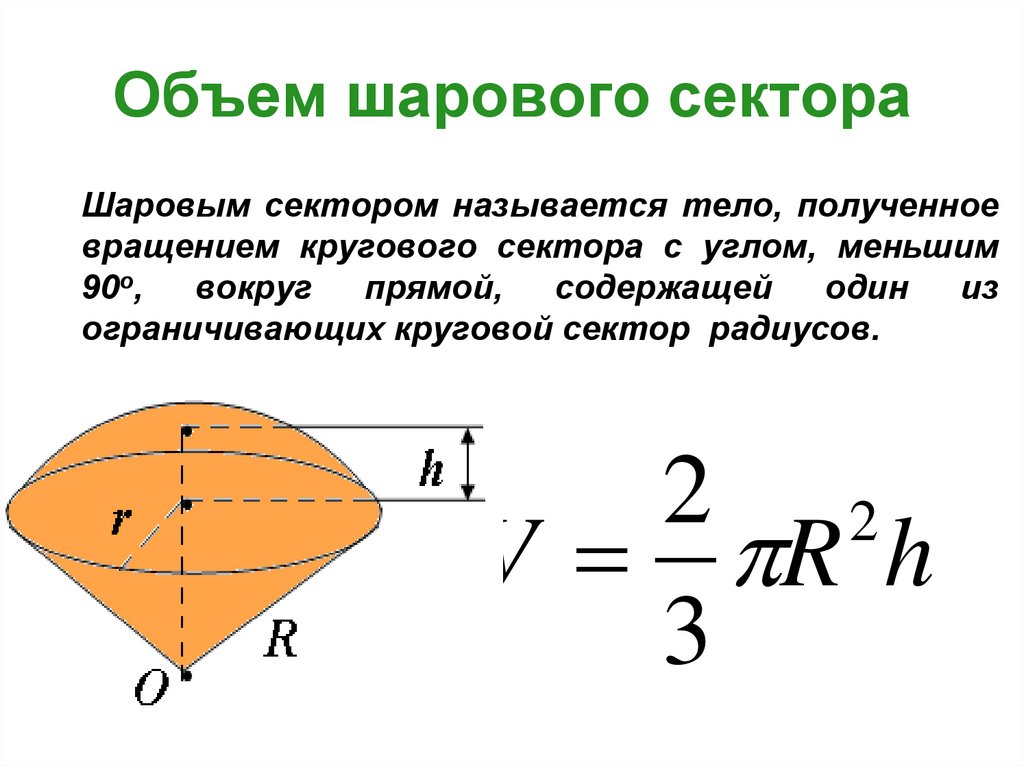
18. Объем шарового сектора
Шаровым сектором называется тело, полученноевращением кругового сектора с углом, меньшим
90о,
вокруг
прямой,
содержащей
один
из
ограничивающих круговой сектор радиусов.
2 2
V R h
3










 Математика
Математика








