Похожие презентации:
Объёмы тел. Общие свойства объемов тел
1. Объёмы тел
Понятие объёмаСвойства объёмов
Объём прямоугольного параллелепипеда
Объём прямой призмы
Объём наклонной призмы
Объём пирамиды
Объём цилиндра
Объём конуса
Объём шара
Объём шарового сегмента
Объём шарового сектора
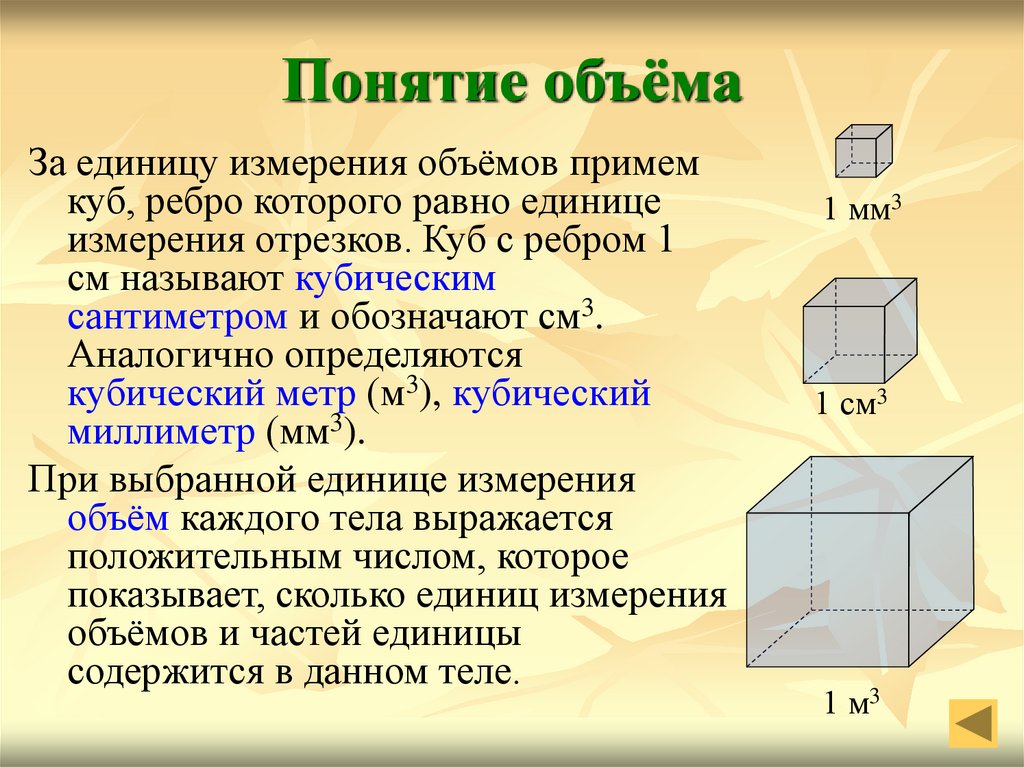
2. Понятие объёма
За единицу измерения объёмов примемкуб, ребро которого равно единице
измерения отрезков. Куб с ребром 1
см называют кубическим
сантиметром и обозначают см3.
Аналогично определяются
кубический метр (м3), кубический
миллиметр (мм3).
При выбранной единице измерения
объём каждого тела выражается
положительным числом, которое
показывает, сколько единиц измерения
объёмов и частей единицы
содержится в данном теле.
1 мм3
1 см3
1 м3
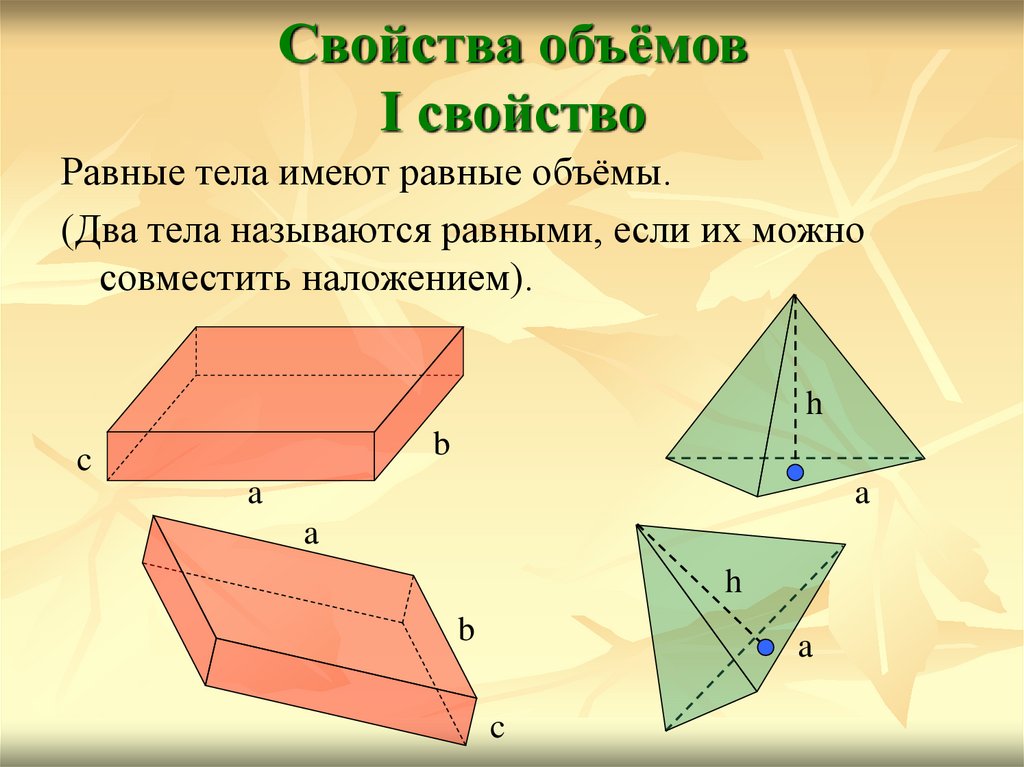
3. Свойства объёмов I свойство
Равные тела имеют равные объёмы.(Два тела называются равными, если их можно
совместить наложением).
h
b
c
a
a
a
h
b
a
c
4.
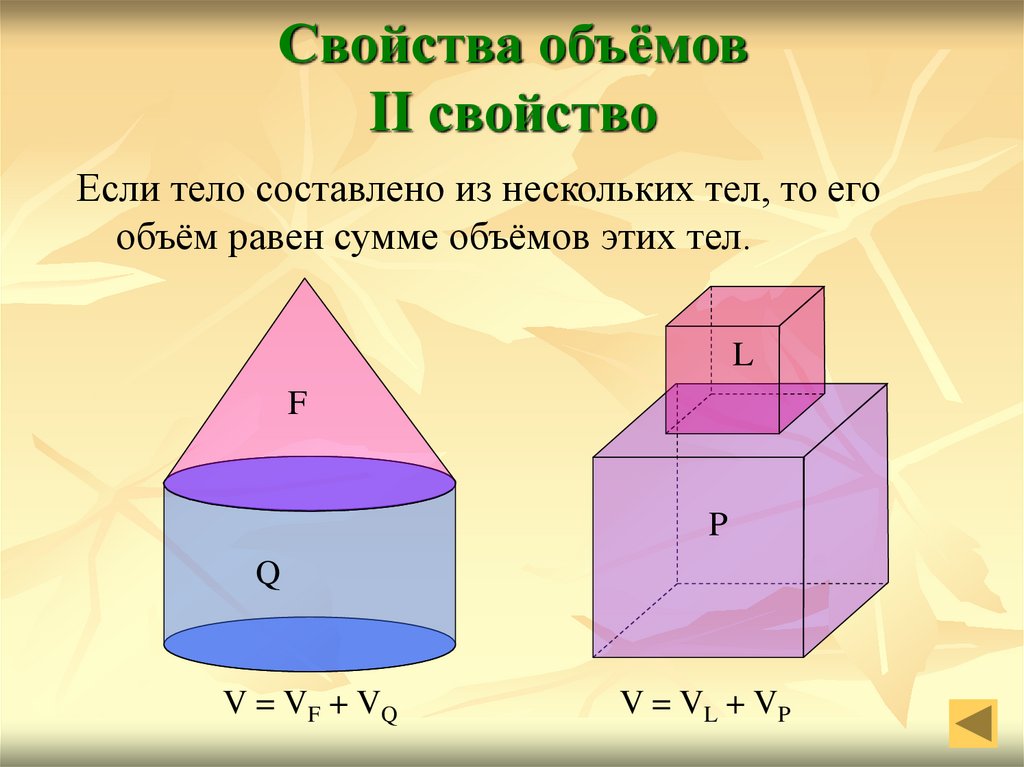
Свойства объёмовII свойство
Если тело составлено из нескольких тел, то его
объём равен сумме объёмов этих тел.
L
F
P
Q
V = VF + VQ
V = VL + VP
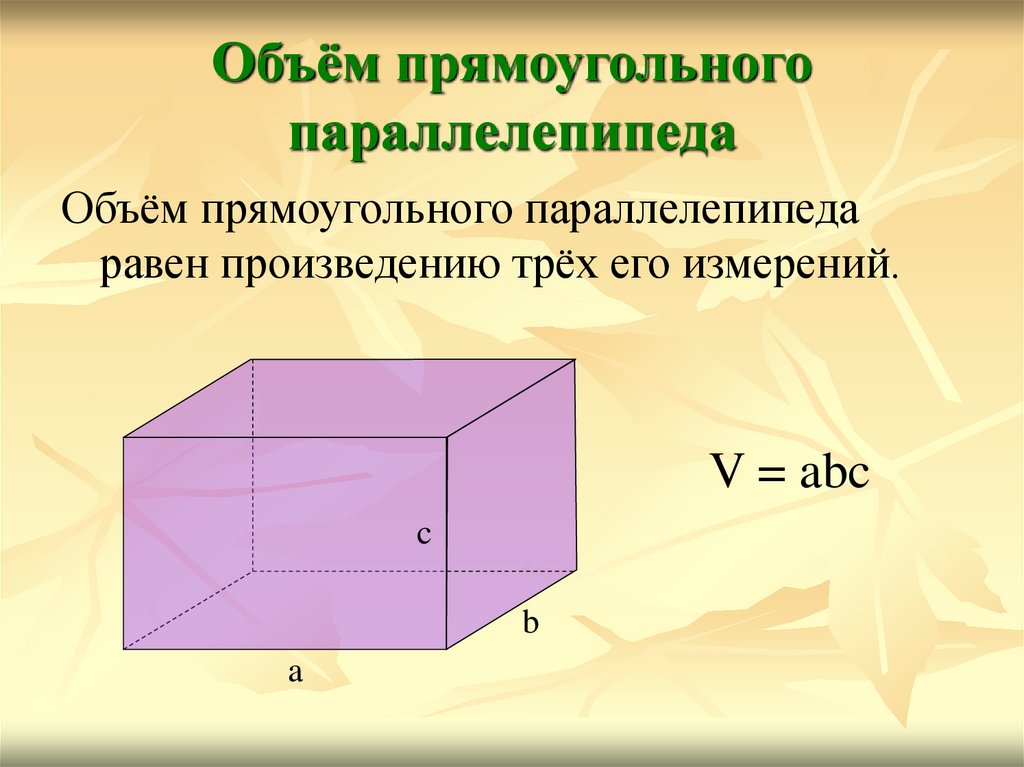
5. Объём прямоугольного параллелепипеда
Объём прямоугольного параллелепипедаравен произведению трёх его измерений.
V = abc
c
b
a
6.
Объём прямоугольногопараллелепипеда
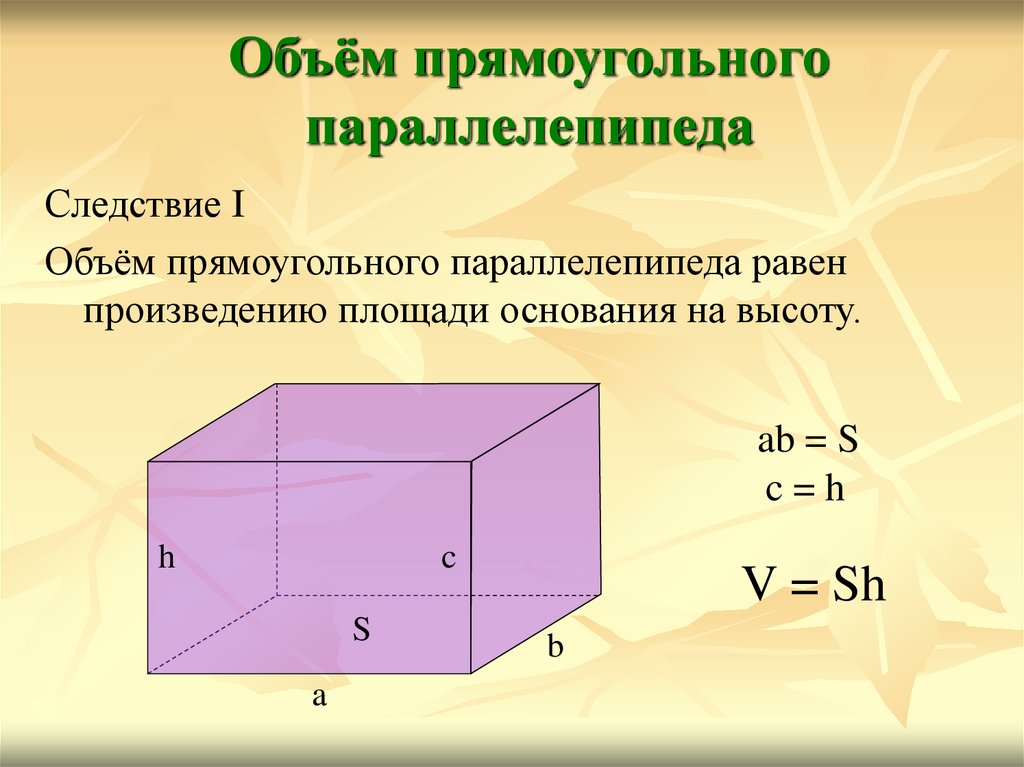
Следствие I
Объём прямоугольного параллелепипеда равен
произведению площади основания на высоту.
ab = S
c=h
h
c
S
a
V = Sh
b
7.
Объём прямоугольногопараллелепипеда
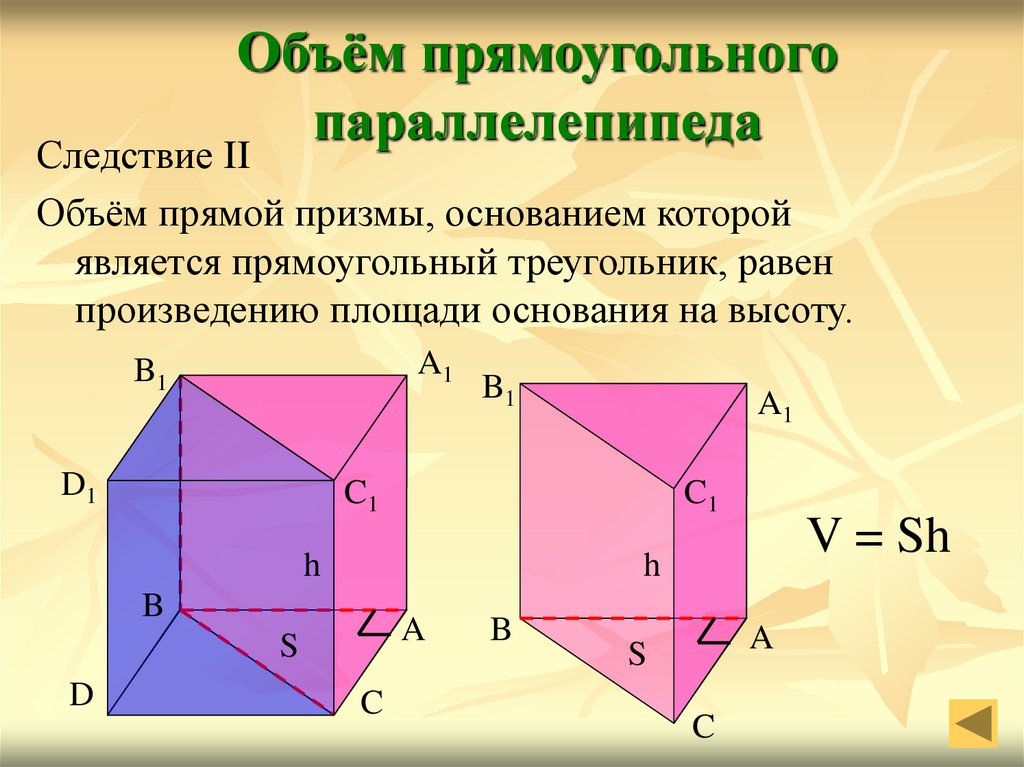
Следствие II
Объём прямой призмы, основанием которой
является прямоугольный треугольник, равен
произведению площади основания на высоту.
A1
B1
D1
B1
C1
C1
h
V = Sh
h
B
A
S
D
A1
C
B
A
S
C
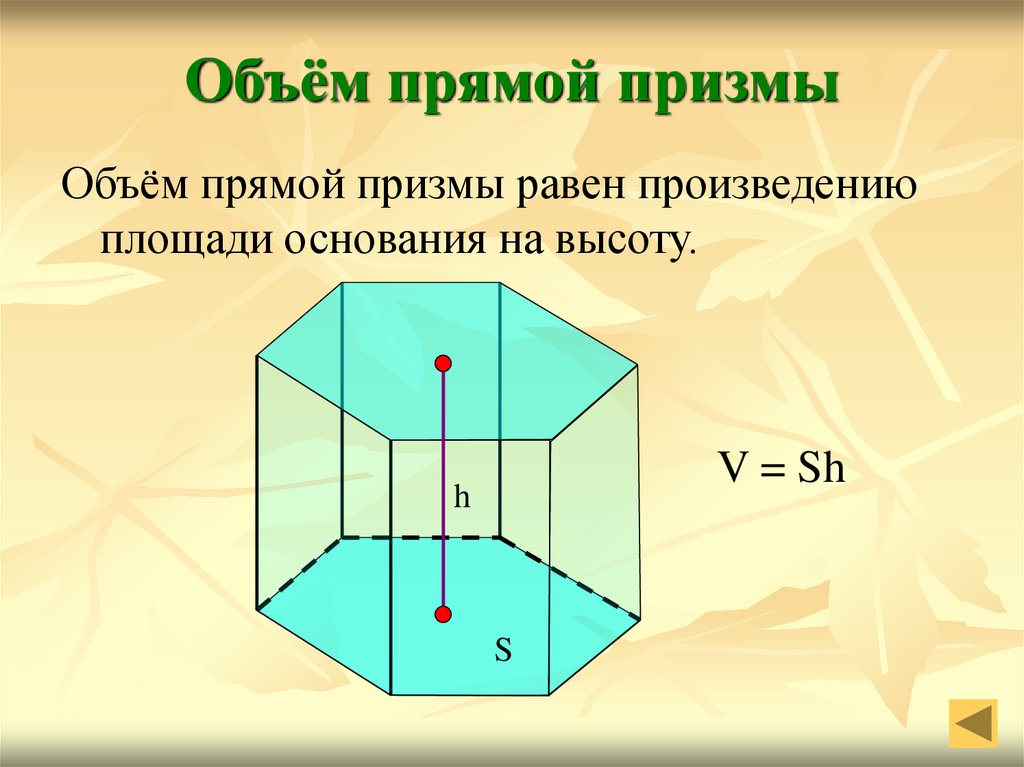
8. Объём прямой призмы
Объём прямой призмы равен произведениюплощади основания на высоту.
V = Sh
h
S
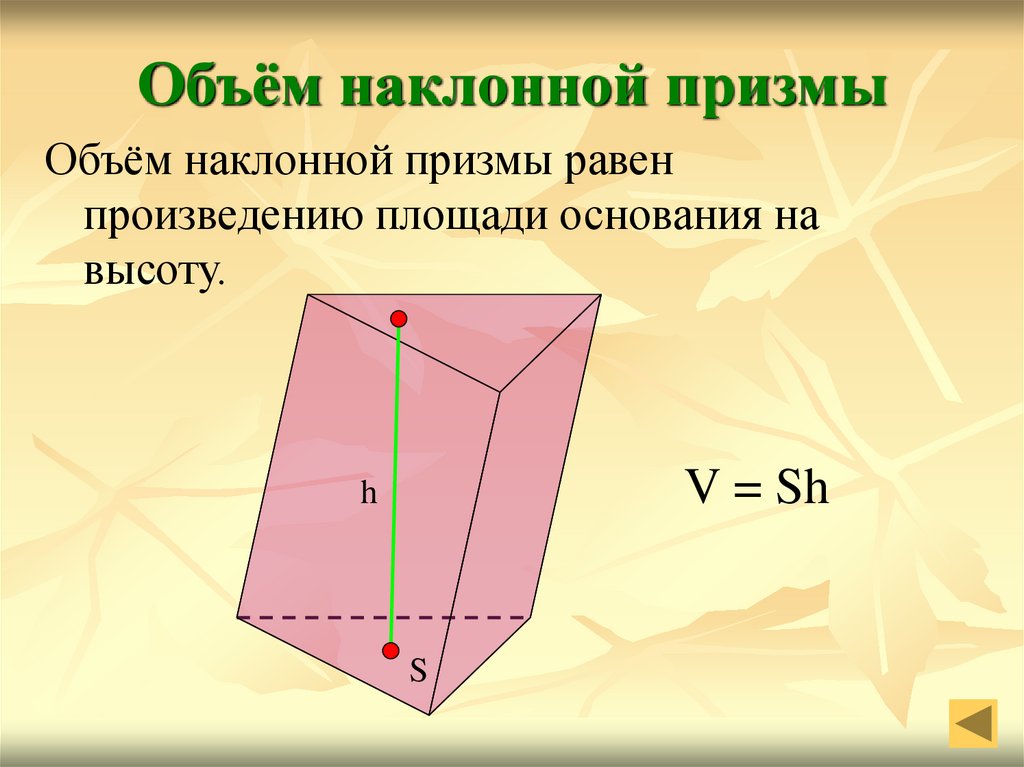
9. Объём наклонной призмы
Объём наклонной призмы равенпроизведению площади основания на
высоту.
V = Sh
h
S
10.
№ 25579.3
4
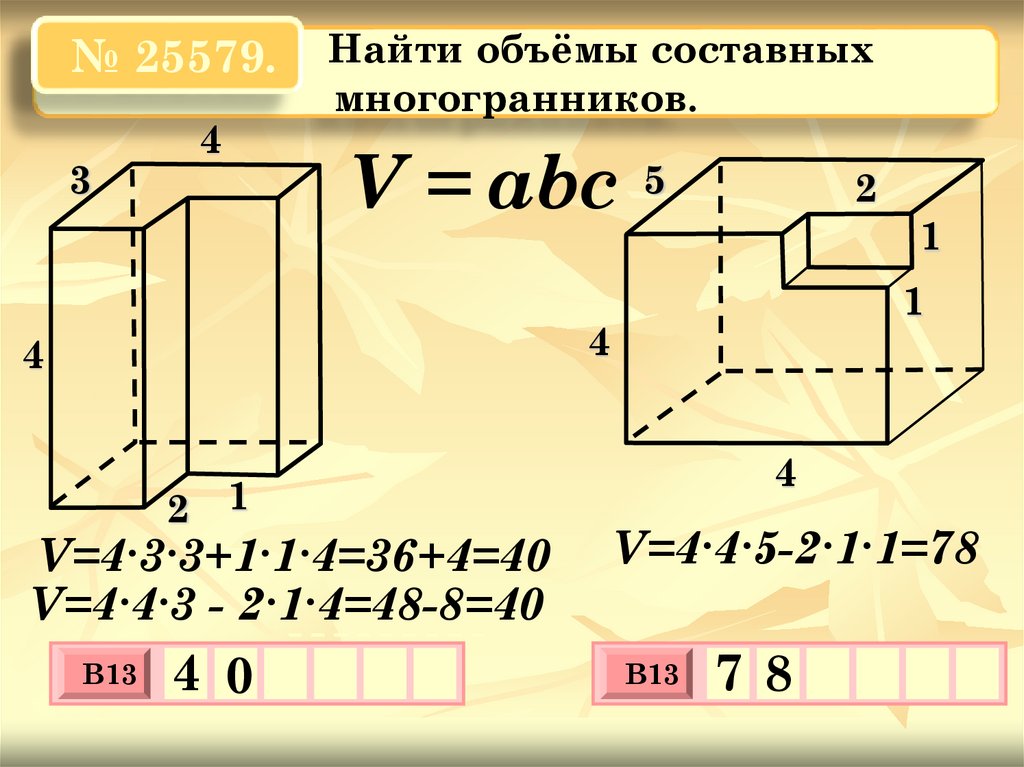
Найти объёмы составных
многогранников.
V = abc
5
2
1
1
4
4
4
2 1
V=4∙3∙3+1∙1∙4=36+4=40
V=4∙4∙3 - 2∙1∙4=48-8=40
В13
4 0
3
10 х
х
V=4∙4∙5-2∙1∙1=78
В13
7 8
3
10 х
х
11.
Термин “пирамида” заимствованиз греческого “пирамис” или “пирамидос”. Греки в
свою очередь позаимствовали это слово, как
полагают, из египетского языка. В папирусе
Ахмеса встречается слово “пирамус” в смысле
ребра правильной пирамиды. Другие считают,
что термин берет свое начало от форм хлебцев в
Древней Греции “пирос” - рожь). В связи с тем,
что форма пламени иногда напоминает образ
пирамиды, некоторые средневековые ученые
считали, что термин происходит от греческого
слова “пир” - огонь. Вот почему в некоторых
учебниках геометрии XVI в. пирамида названа
“огнеформное тело”.
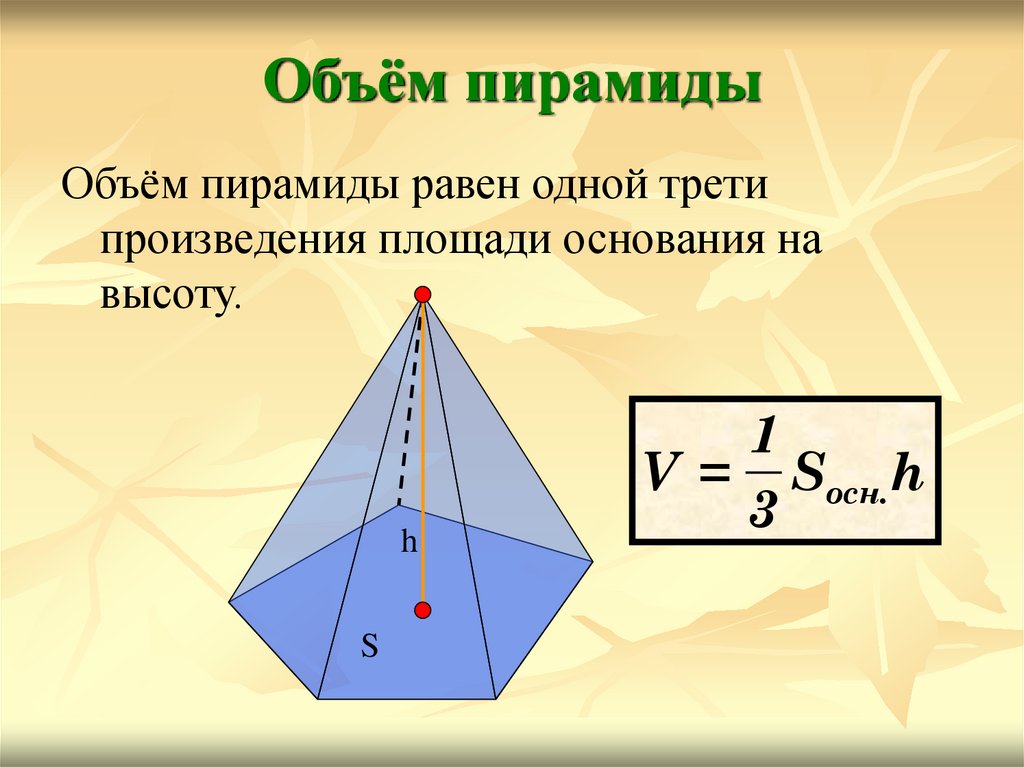
12. Объём пирамиды
Объём пирамиды равен одной третипроизведения площади основания на
высоту.
h
S
11
VV= SSh
осн. h
33
13.
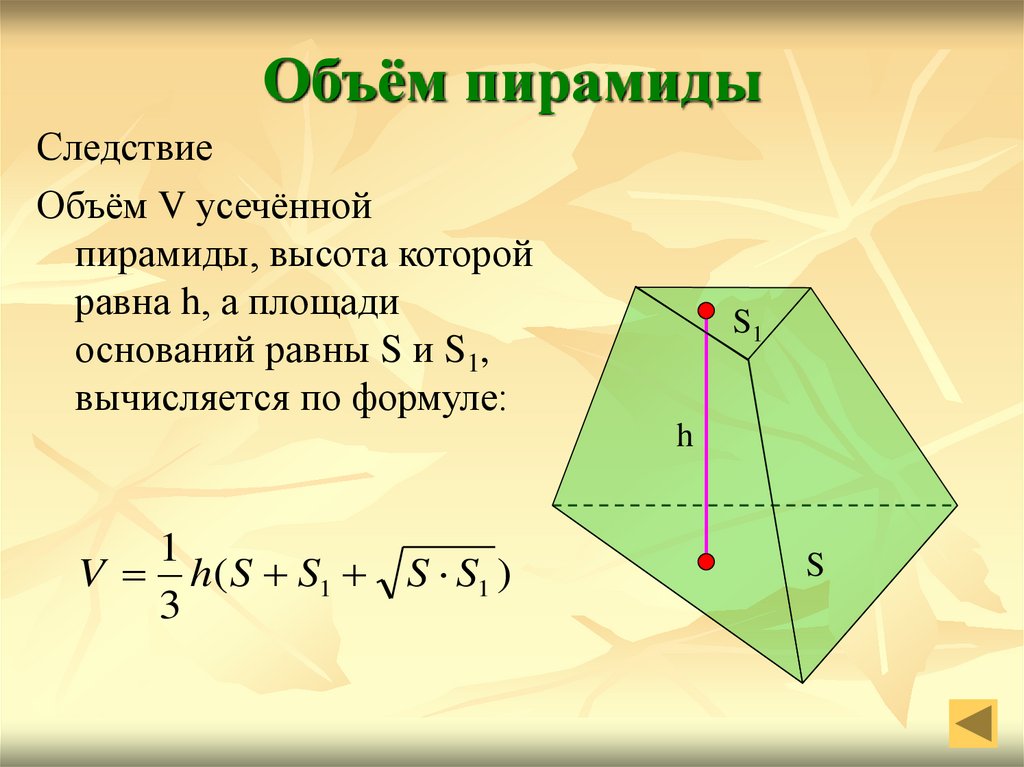
Объём пирамидыСледствие
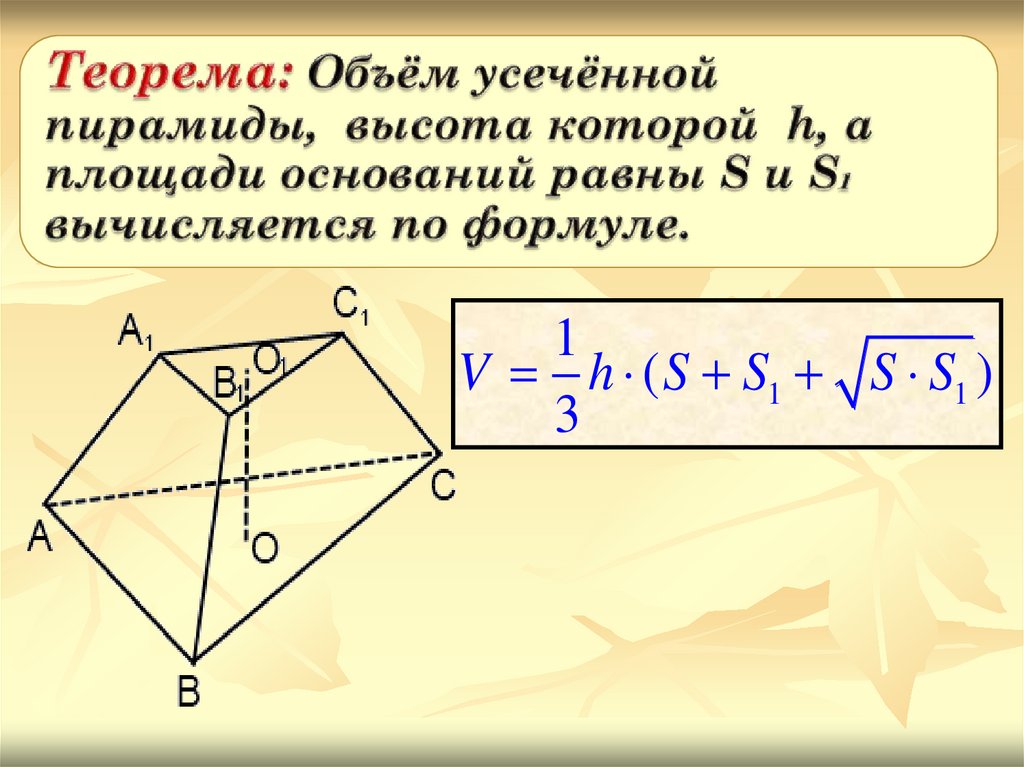
Объём V усечённой
пирамиды, высота которой
равна h, а площади
оснований равны S и S1,
вычисляется по формуле:
S1
h
1
V h( S S1 S S1 )
3
S
14.
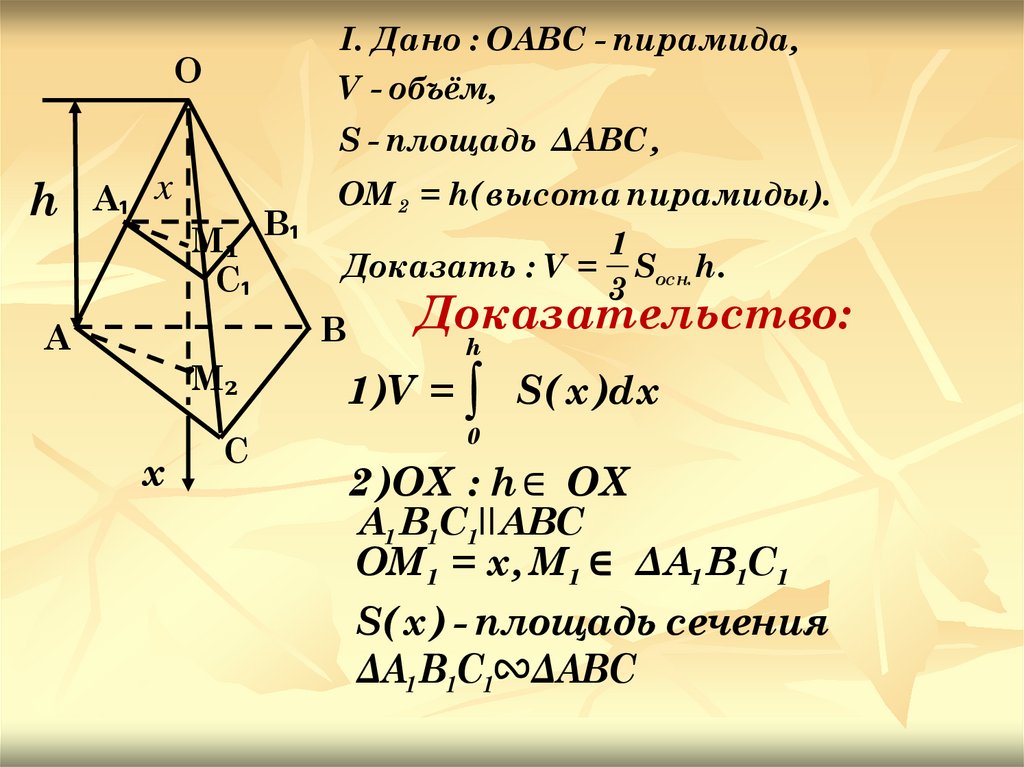
I. Дано : ОАВС - пирамида,O
V - объём,
S - площадь ΔАВС ,
h
А₁ x
М₁ В₁
С₁
ОМ 2 = h( высота пирамиды).
1
Доказать : V = Sосн. h.
3
В
А
М₂
х
С
Доказательство:
h
1 )V = ∫ S( x )dx
0
2 )OX : h ∈ OX
А1 В1С1IIАВС
ОМ 1 = х , М1 ∈ ΔА1 В1С1
S( x ) - площадь сечения
ΔА1 В1С1 ΔАВС
15.
Oh
А₁
А
х
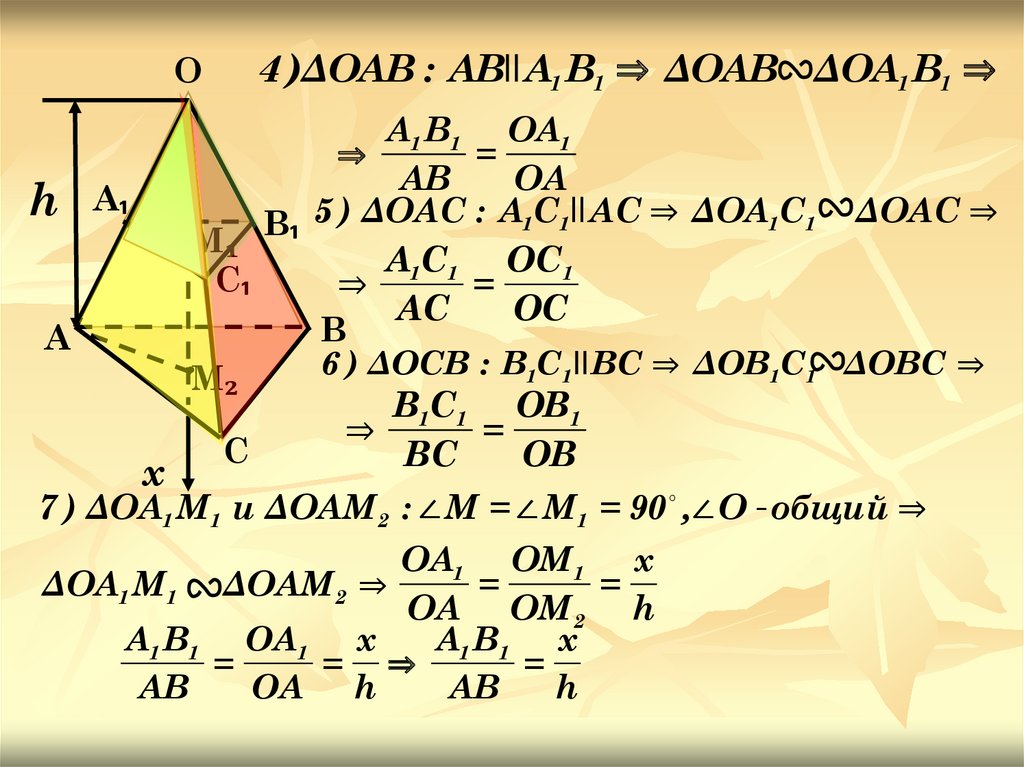
4 )ΔОАВ : АВIIА1 В1 ⇒ ΔОАВ ΔОА1 В1 ⇒
А1 В1 ОА1
⇒
=
АВ
ОА
5 ) ΔОАС : А1С1II АС ⇒ ΔОА1С1 ΔОАС ⇒
В₁
М₁
А1С1 ОС1
С₁
⇒
=
АС
ОС
В
6 ) ΔОСВ : В1С1II ВС ⇒ ΔОВ1С1 ΔОВС ⇒
М₂
В1С1 ОВ1
⇒
=
С
ВС
ОВ
7 ) ΔОА1 М 1 и ΔОAМ 2 : ∠ М = ∠ М 1 = 90 ,∠ О - общий ⇒
ОА1 ОМ 1 х
ΔОА1 М 1 ΔОAМ 2 ⇒
=
=
ОА ОМ 2 h
А1 В1 ОА1 х
А1 В1 х
=
= ⇒
=
АВ
ОА h
АВ
h
16.
Oh
А1С1 х В1С1 х
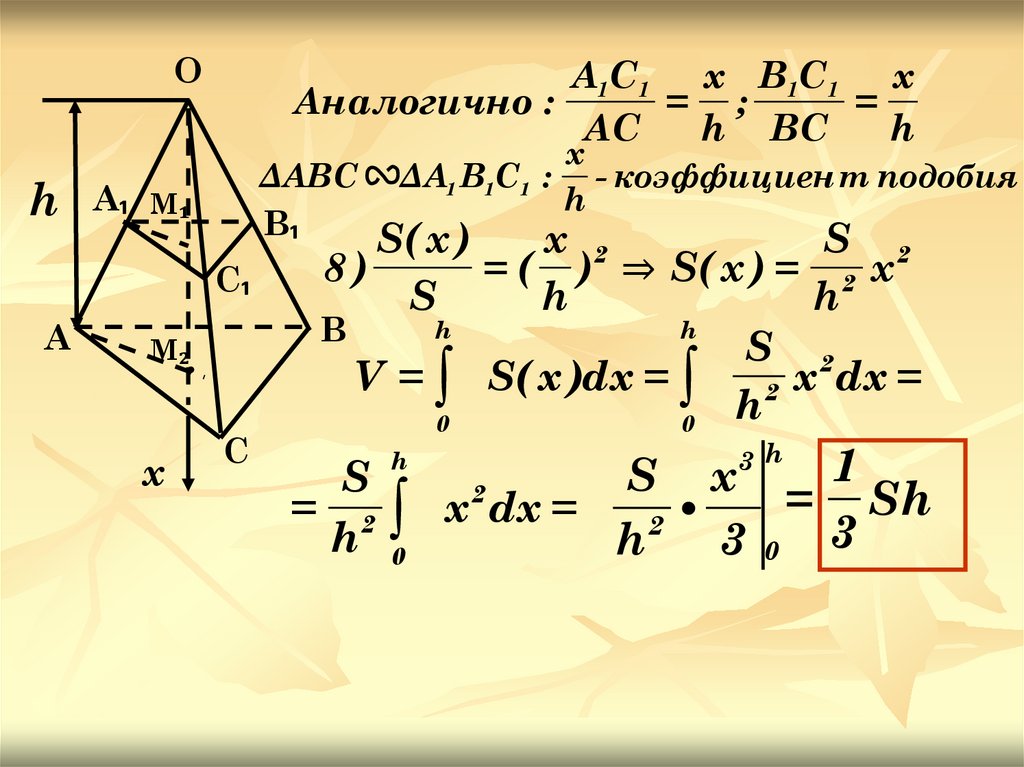
Аналогично :
= ;
=
АС
h ВС
h
ΔАВС
В₁
А₁ М₁
С₁
А
М₂
х
С
х
ΔА1 В1С1 : - коэффициен т подобия
h
S( x )
x 2
S 2
8)
= ( ) ⇒ S( x ) = 2 x
S
h
h
h
h
В
S 2
V = ∫ S( x )dx = ∫
2 x dx =
h
0
0
S
= 2
h
h
∫
0
1
S
x
= Sh
x 2 dx =
2
h
30 3
3 h
17.
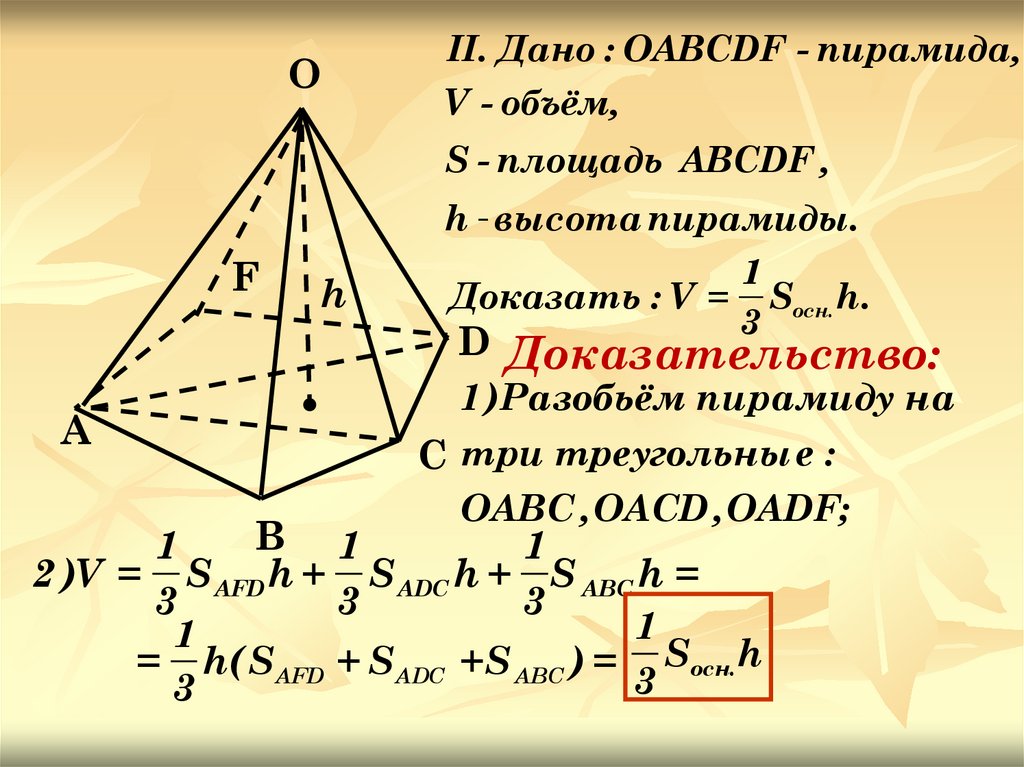
ОII. Дано : ОАВСDF - пирамида,
V - объём,
S - площадь АВСDF ,
h - высота пирамиды.
F
h
1
Доказать : V = Sосн. h.
3
D Доказательство:
А
1 )Разобьём пирамиду на
С три треугольны е :
ОАВС , ОАСD , ОАDF;
В 1
1
1
2 )V = S AFD h + S ADC h + S ABC h =
3
3
3
1
1
= h( SAFD + S ADC +S ABC ) = Sосн. h
3
3
18.
1V h ( S S1 S S1 )
3
19.
Объем усеченной пирамиды будемрассматривать как разность
объемов полной пирамиды и той,
что отсечена от нее плоскостью,
параллельной основанию
20.
Объем полнойпирамиды
1
V Sh
3
x
S1
h
S
1
1
1
1
1
V Sh Sx S1 x Sh x( S S1 )
3
3
3
3
3
S (h x) 2
S1
x2
h S1
x
S S1
(1)
S x S1 h S1 x
S x S1 x S1 h
Подставляем в уравнение 1
h S1
1
1
V Sh ( S S1 )
3
3
S S1
h S1
1
1
Sh ( S S1 )( S S1 )
3
3
S S1
1
1
1
1
Sh S1h h SS1 h( S S1 SS1 )
3
3
3
3
21.
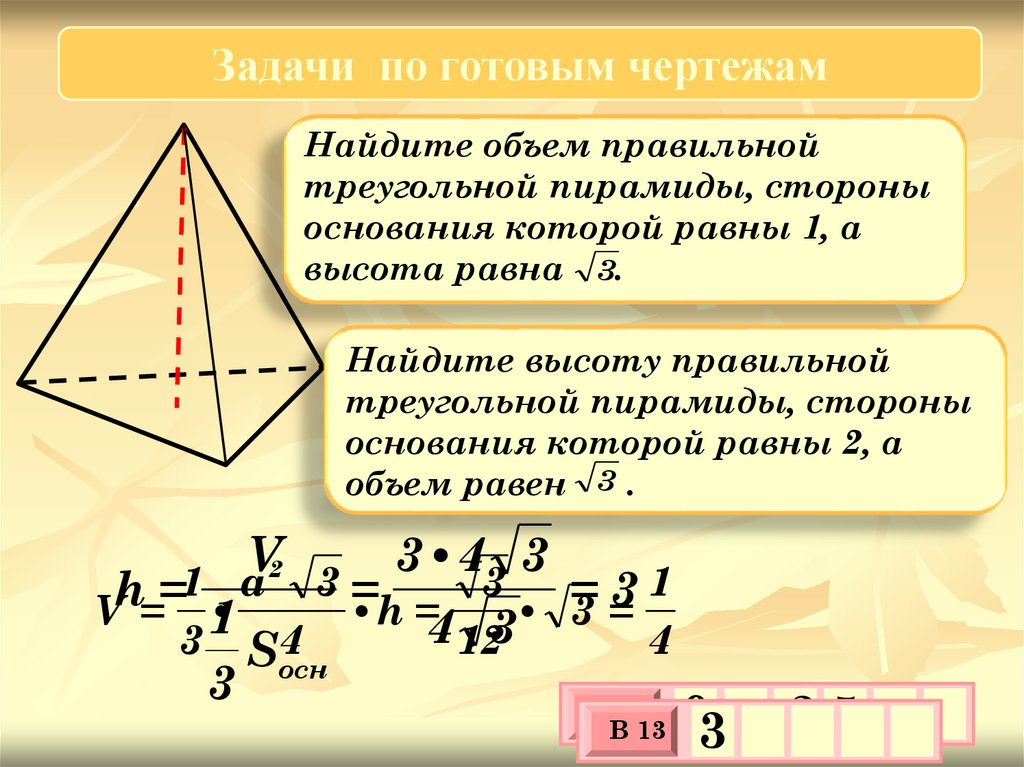
Задачи по готовым чертежамНайдите объем правильной
треугольной пирамиды, стороны
основания которой равны 1, а
высота равна 3.
Найдите высоту правильной
треугольной пирамиды, стороны
основания которой равны 2, а
объем равен 3 .
V2
3 •4 3
1 a 3=
3
1
h
=
=
3
V= 1
• h =4 3• 3 =
3 S4
12
4
3 осн
В 13
25
В 13 03 ,
3
1 03 х
10 х
х
х
22.
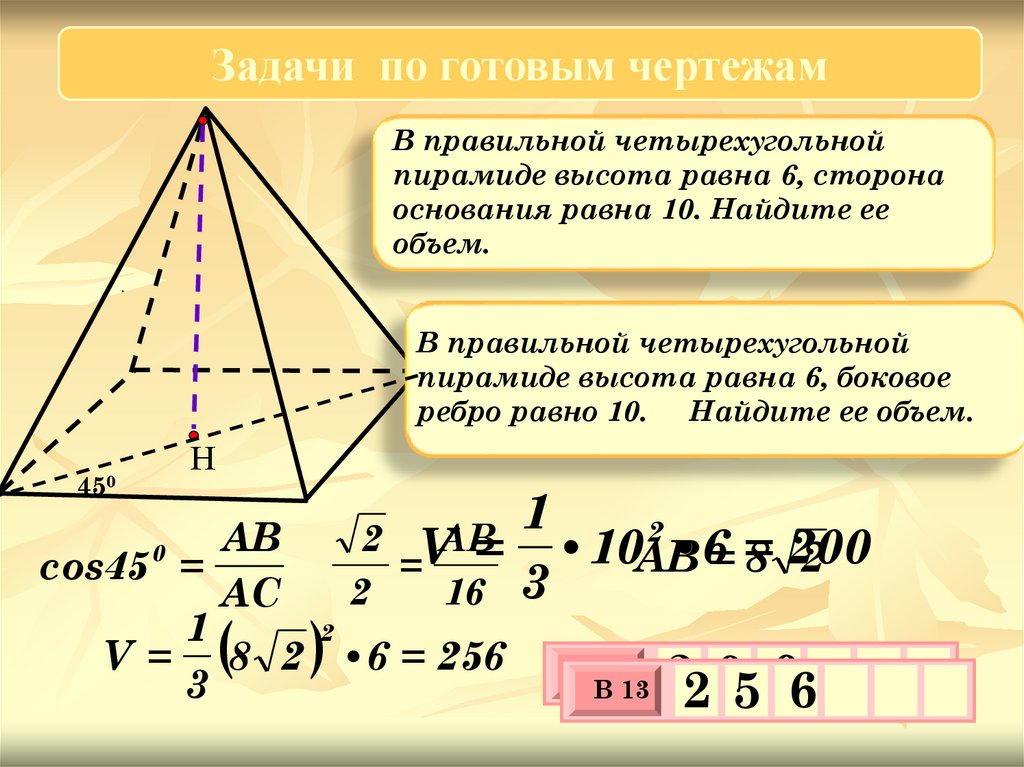
Задачи по готовым чертежамВ правильной четырехугольной
пирамиде высота равна 6, сторона
основания равна 10. Найдите ее
объем.
.
В правильной четырехугольной
пирамиде высота равна 6, боковое
ребро равно 10. Найдите ее объем.
Н
450
1
2
AB
•6= 8
= 200
2
=V = •10AB
16 3
2
AB
сos45 =
2
AC
1
2
V = 8 2 •6 = 256
3
0
(
)
В 13
В 13
22 05 06
3
1 03 х
10 х
х
х
23.
Задачи (база)Сторона основания правильной
треугольной пирамиды равна 6, а
V =18 с плоскостью
боковое ребро образует
основания угол 450. Найдите объем
пирамиды.
Высота правильной треугольной
пирамиды равна 4 3 , а боковая грань
V = 192 основания угол
образует с плоскостью
600. Найдите объем пирамиды.
24.
Задачи (профиль)Объем треугольной пирамиды SABC,
являющейся частью правильной
V = 48
шестиугольной пирамиды SABCDEF, равен 8.
Найдите объем шестиугольной пирамиды.
От треугольной пирамиды, объем которой
равен 12, отсечена треугольная пирамида
плоскостью, проходящей через вершину
=3 основания.
пирамиды и среднююV
линию
Найдите объем отсеченной треугольной
пирамиды.
25. Объём цилиндра
Объём цилиндра равен произведениюплощади основания на высоту.
V r h
2
h
r
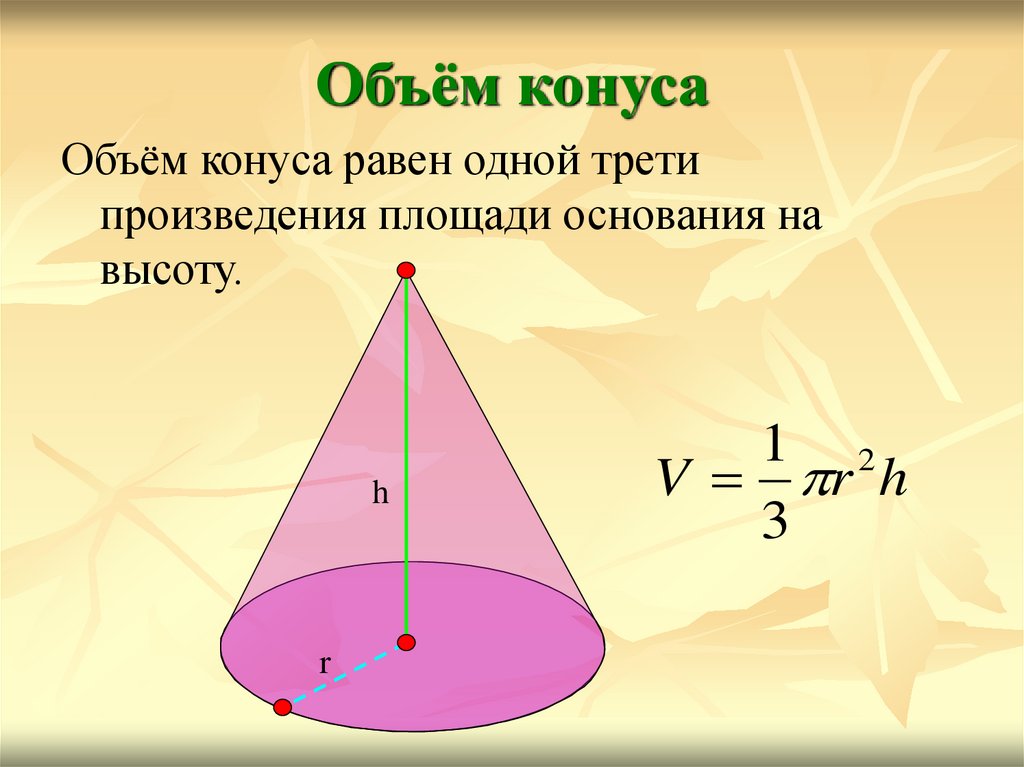
26. Объём конуса
Объём конуса равен одной третипроизведения площади основания на
высоту.
h
r
1 2
V r h
3
27.
Объём конусаСледствие
Объём V усечённого конуса,
высота которого равна h, а
площади оснований равны S
и S1, вычисляется по
формуле:
1
V h( S S1
3
S S1 )
r1
S1
h
r
S
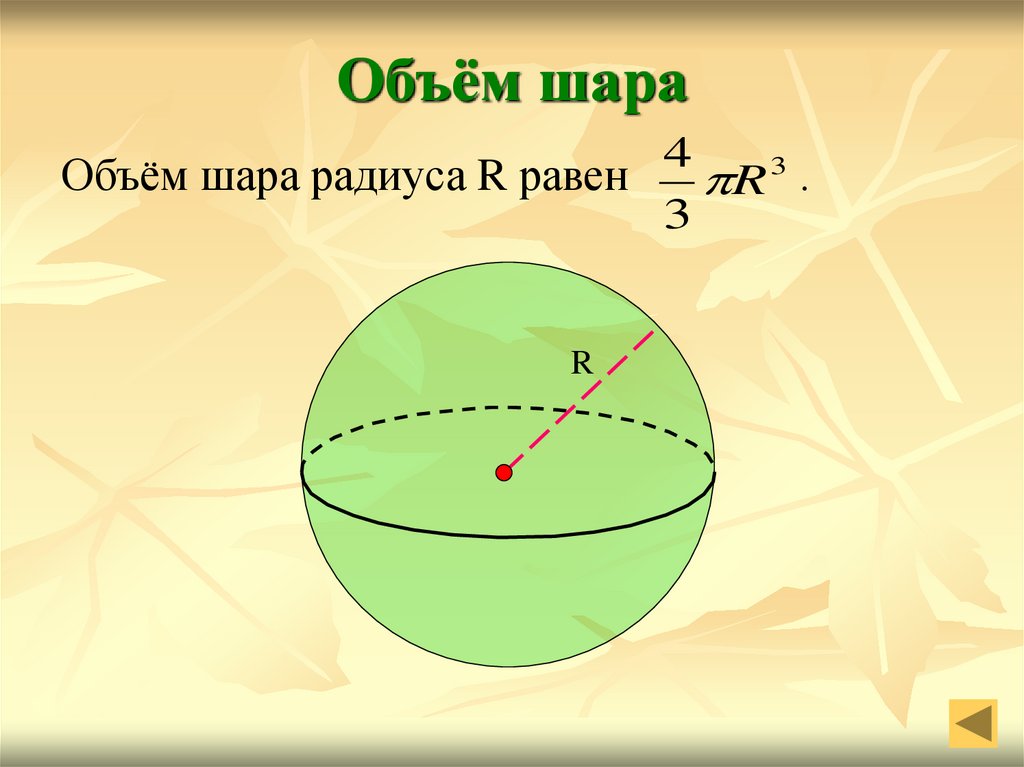
28. Объём шара
43
Объём шара радиуса R равен
R .
3
R
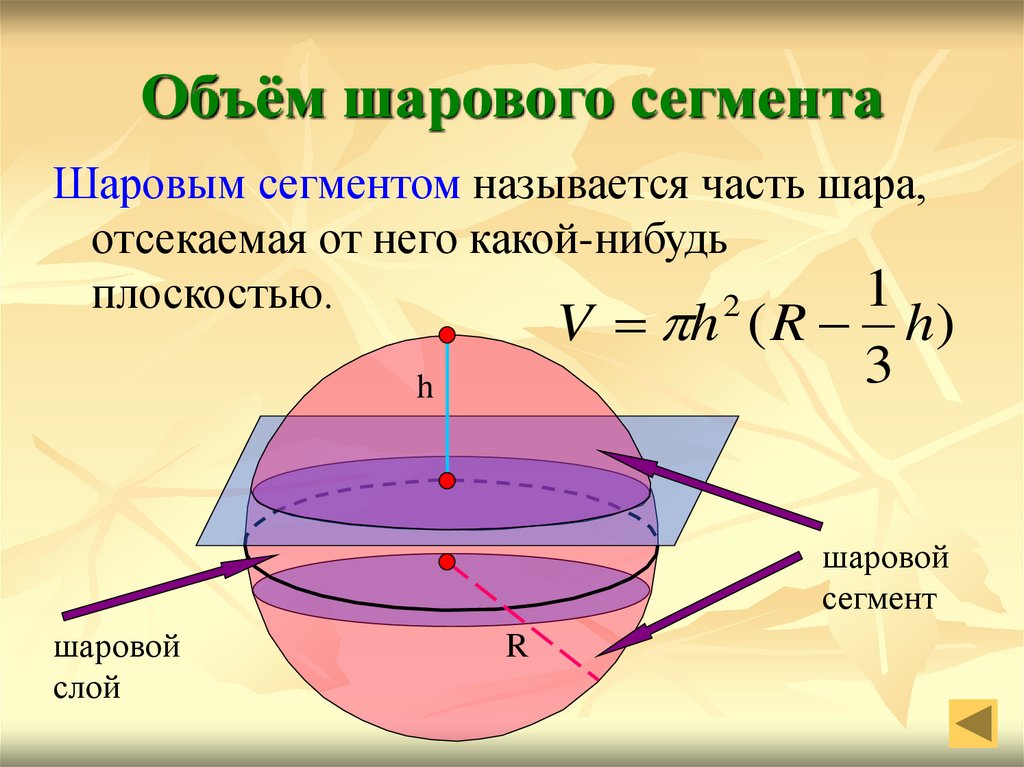
29. Объём шарового сегмента
Шаровым сегментом называется часть шара,отсекаемая от него какой-нибудь
1
плоскостью.
2
V h ( R h)
3
h
шаровой
сегмент
шаровой
слой
R
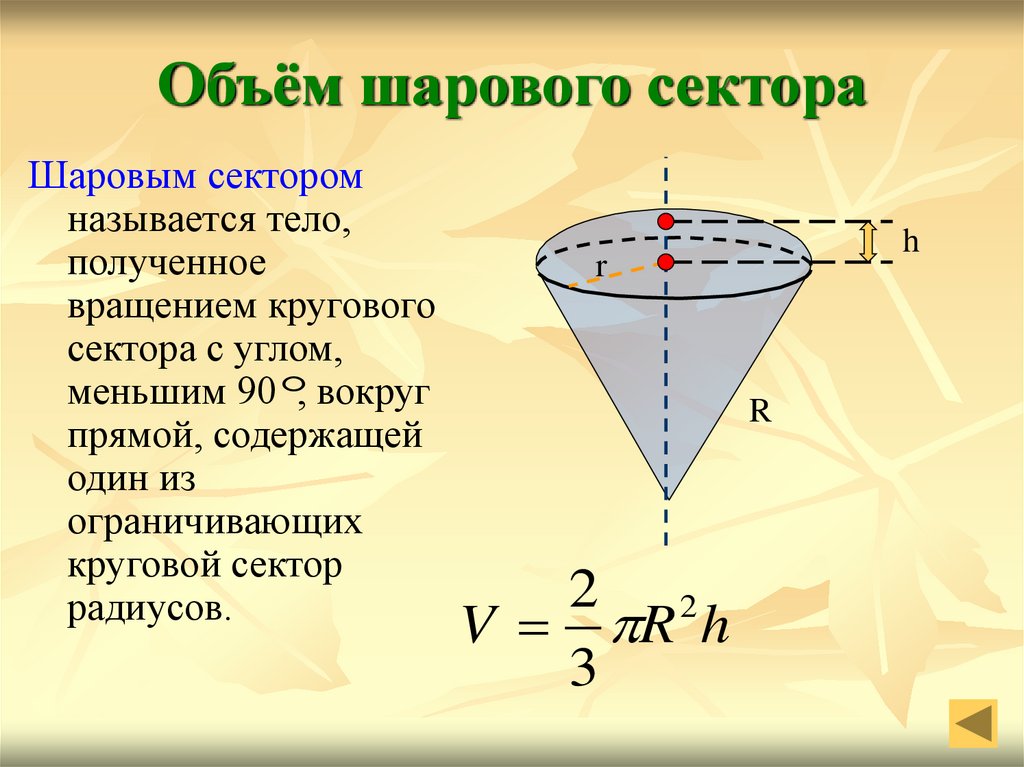
30. Объём шарового сектора
Шаровым секторомназывается тело,
полученное
вращением кругового
сектора с углом,
меньшим 90 , вокруг
прямой, содержащей
один из
ограничивающих
круговой сектор
радиусов.
h
r
R
2 2
V R h
3







 Математика
Математика








