Похожие презентации:
Асимптоты графика функции
1.
Асимптоты графика функции.Опр. Асимптотой графика функции y=f(x)
называется прямая, к которой неограниченно
приближается точка графика функции при
неограниченном удалении от начала координат.
2.
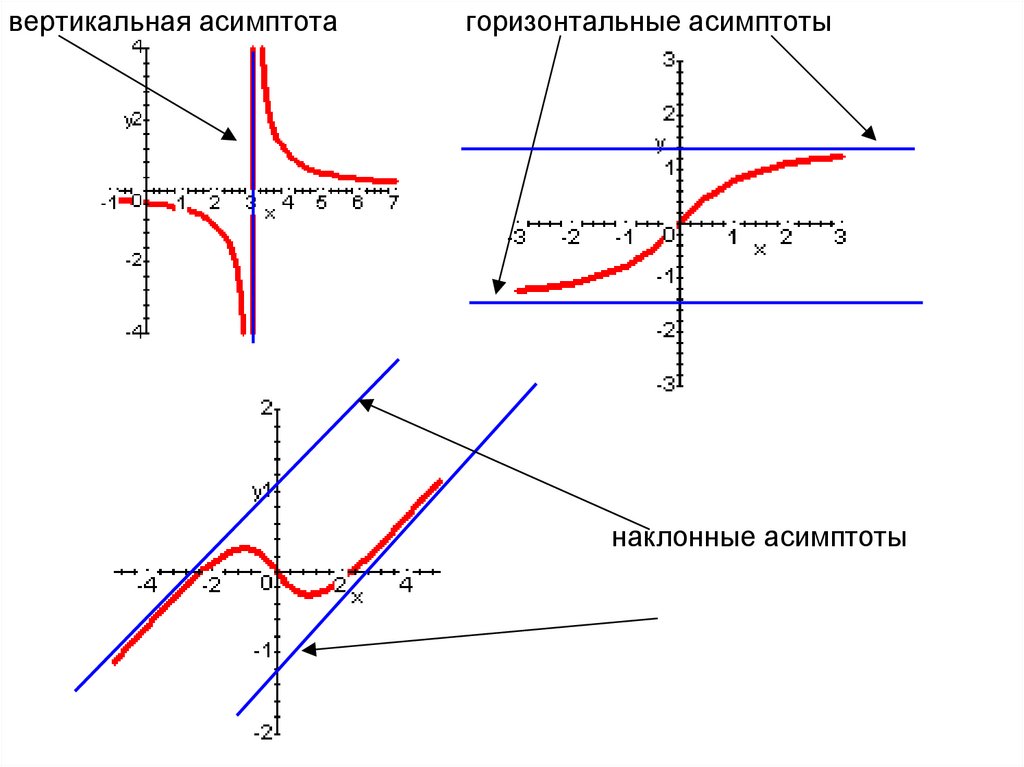
вертикальная асимптотагоризонтальные асимптоты
наклонные асимптоты
3.
Асимптоты графика функции.Теорема 1. Если
то прямая x=a является вертикальной асимптотой
графика функции y=f(x).
4.
Асимптоты графика функции.Cледствие. Вертикальные асимптоты следует
искать в точках разрыва области определения и
на концах ее области определения (если
область определения имеет вид
(a,b), (a,+∞), (-∞,b)).
5.
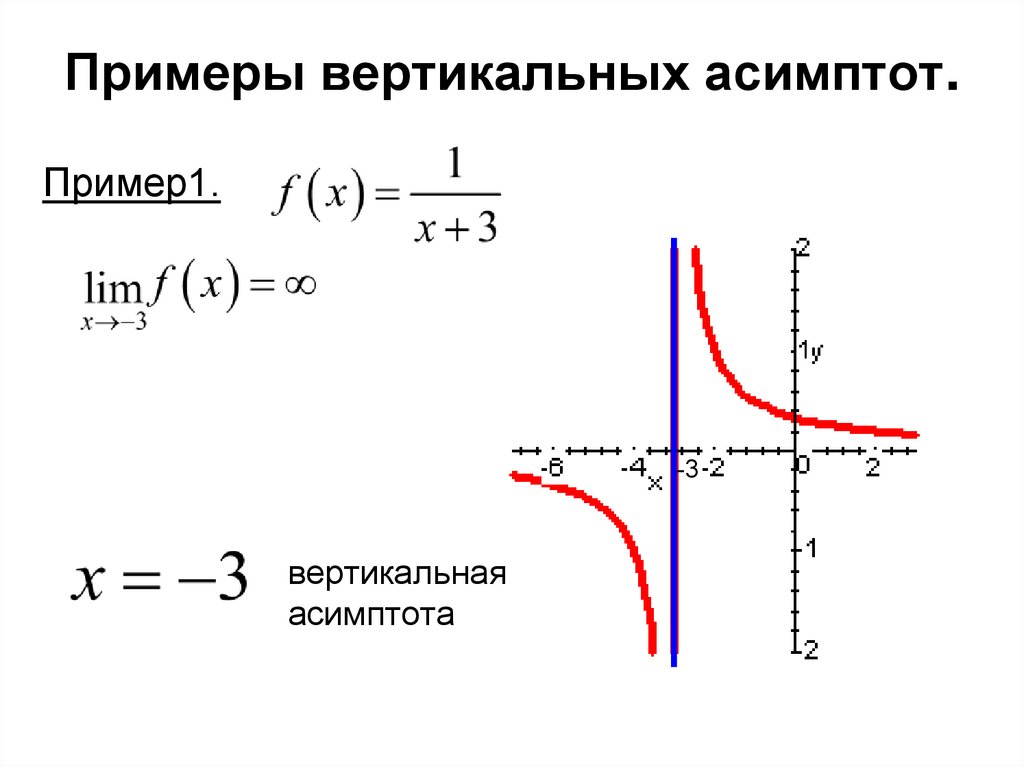
Примеры вертикальных асимптот.Пример1.
6.
Примеры вертикальных асимптот.Пример1.
-3
вертикальная
асимптота
7.
Примеры вертикальных асимптот.Пример 2.
8.
Асимптоты графика функции.Теорема 2. Если
, то прямая y=a
является горизонтальной асимптотой.
9.
Примеры горизонтальных асимптот.Пример1.
10.
Примеры горизонтальных асимптот.Пример1.
горизонтальная
асимптота
-3
11.
Асимптоты графика функции.Теорема 3. Если
,
то прямая y=ax+b является наклонной асимптотой.
12.
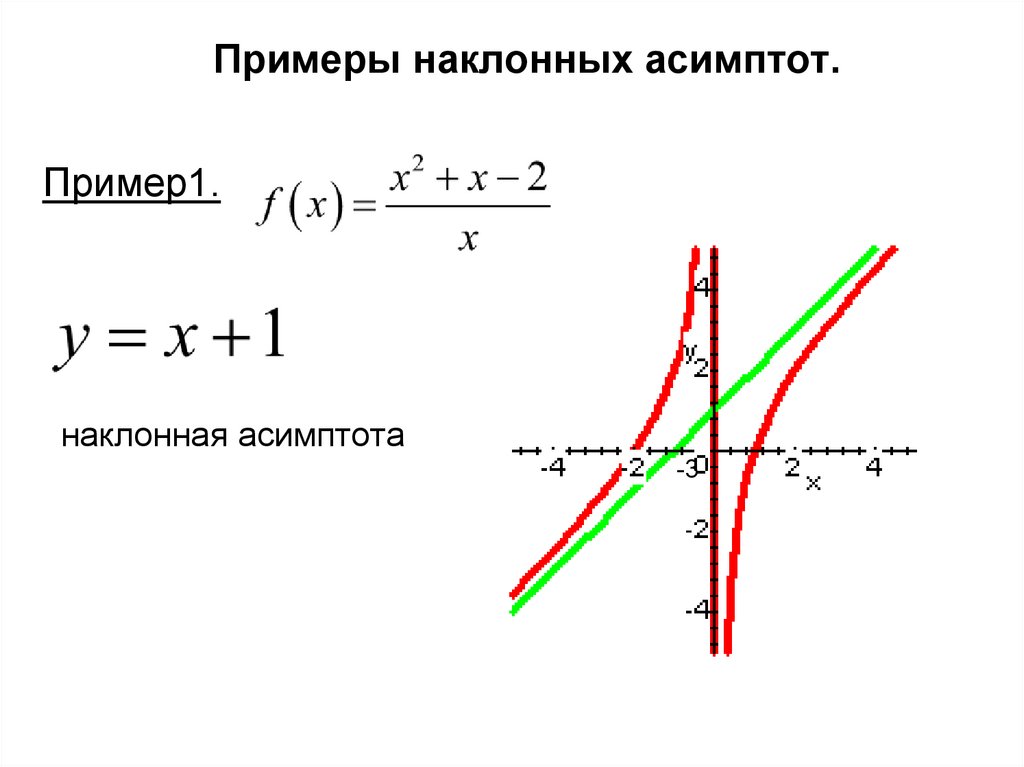
Примеры наклонных асимптот.Пример1.
13.
Примеры наклонных асимптот.Пример1.
14.
Примеры наклонных асимптот.Пример1.
наклонная асимптота
-3
15.
Замечание. Горизонтальная асимптота является частным случаемнаклонной асимптоты
y=ax+b
Если а=0, то наклонная асимптота становится горизонтальной.
Поэтому горизонтальные асимптоты можно не искать,
сразу искать наклонные.
16.
Общая схема исследованияфункций.
1. Область определения.
2. Исследование на четность-нечетность.
3. Асимптоты.
4. Экстремумы и интервалы монотонности.
5. Точки перегиба и интервалы выпуклости.
6. Точки пресечения с осями координат.
7. График функции.
17.
Пример1. Область определения
18.
Пример1. Область определения
19.
Пример2. Исследование на четность-нечетность.
f(-x)=……
20.
Пример2. Исследование на четность-нечетность.
Функция общего вида
21.
Пример3. Асимптоты
А) вертикальные
x=3 – точка разрыва
22.
Пример3. Асимптоты
А) вертикальные
x=3 – точка разрыва
x=3 – вертикальная асимптота
23.
Пример3. Асимптоты
б) горизонтальные и наклонные y=ax+b
24.
Пример3. Асимптоты
в) наклонные y=ax+b
25.
Пример3. Асимптоты
в) наклонные y=ax+b
26.
Пример3. Асимптоты
в) наклонные y=ax+b
y=x-3 – наклонная асимптота,
горизонтальных асимптот нет
27.
Пример4. Экстремумы и интервалы монотонности
28.
Пример4. Экстремумы и интервалы монотонности
29.
Пример4. Экстремумы и интервалы монотонности
30.
Пример4. Экстремумы и интервалы монотонности
+
1
т. max
+
3
5
т. min
31.
Пример4. Экстремумы и интервалы монотонности
+
1
т. max
+
3
5
т. min
32.
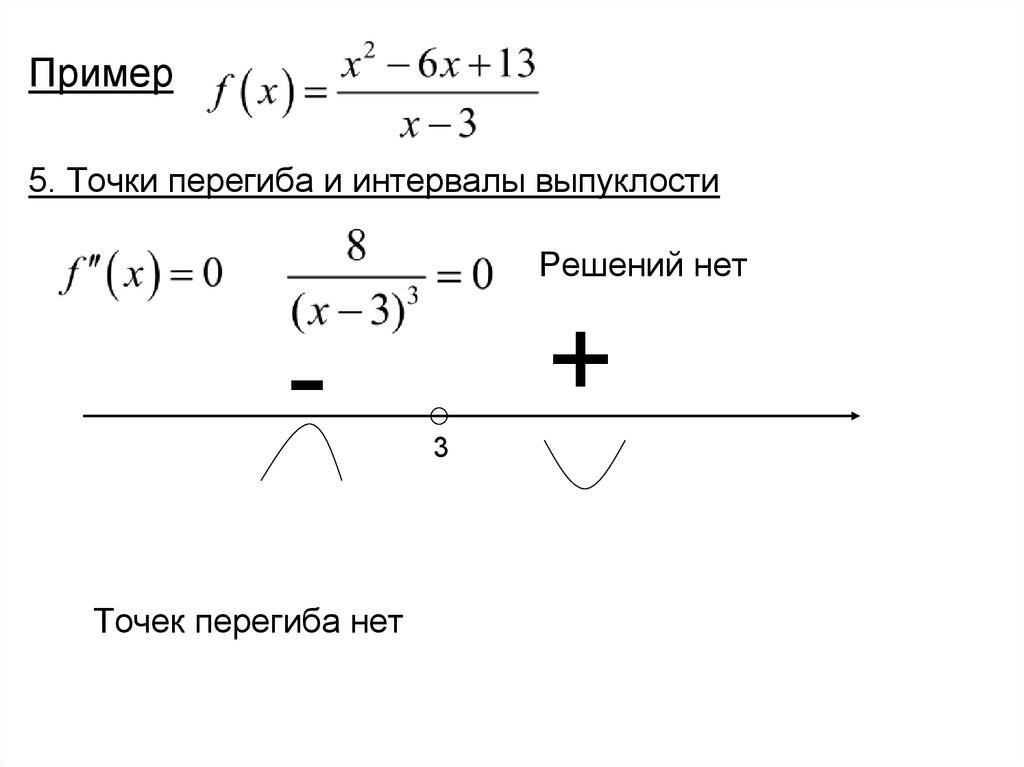
Пример5. Точки перегиба и интервалы выпуклости
33.
Пример5. Точки перегиба и интервалы выпуклости
34.
Пример5. Точки перегиба и интервалы выпуклости
Решений нет
Точек перегиба нет
+
3
35.
Пример6. Точки пересечения с осями координат.
С осью OX y=0
36.
Пример6. Точки пересечения с осями координат.
С осью OX y=0
Точек пересечения с OX нет
37.
Пример6. Точки пересечения с осями координат.
С осью OY x=0
38.
Пример6. Точки пересечения с осями координат.
С осью OY x=0
39.
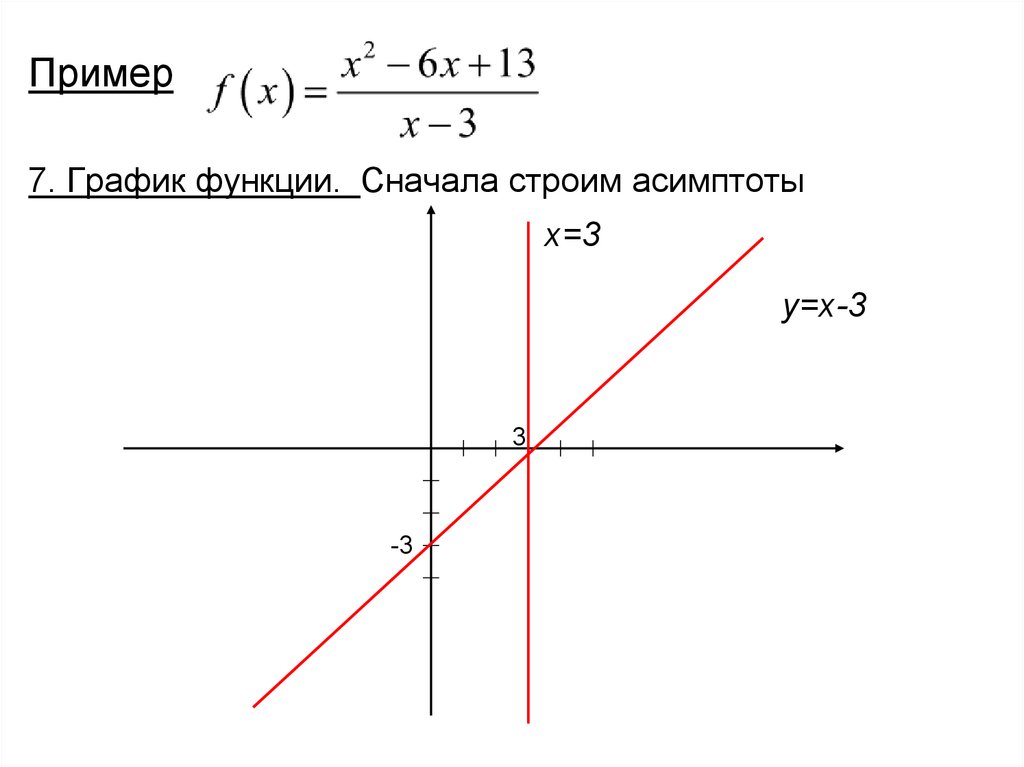
Пример7. График функции. Сначала строим асимптоты
x=3
y=x-3
3
-3
40.
Пример7. График функции. Отмечаем точки экстремума
x=3
y=x-3
4
1
-3
-4
3
5
41.
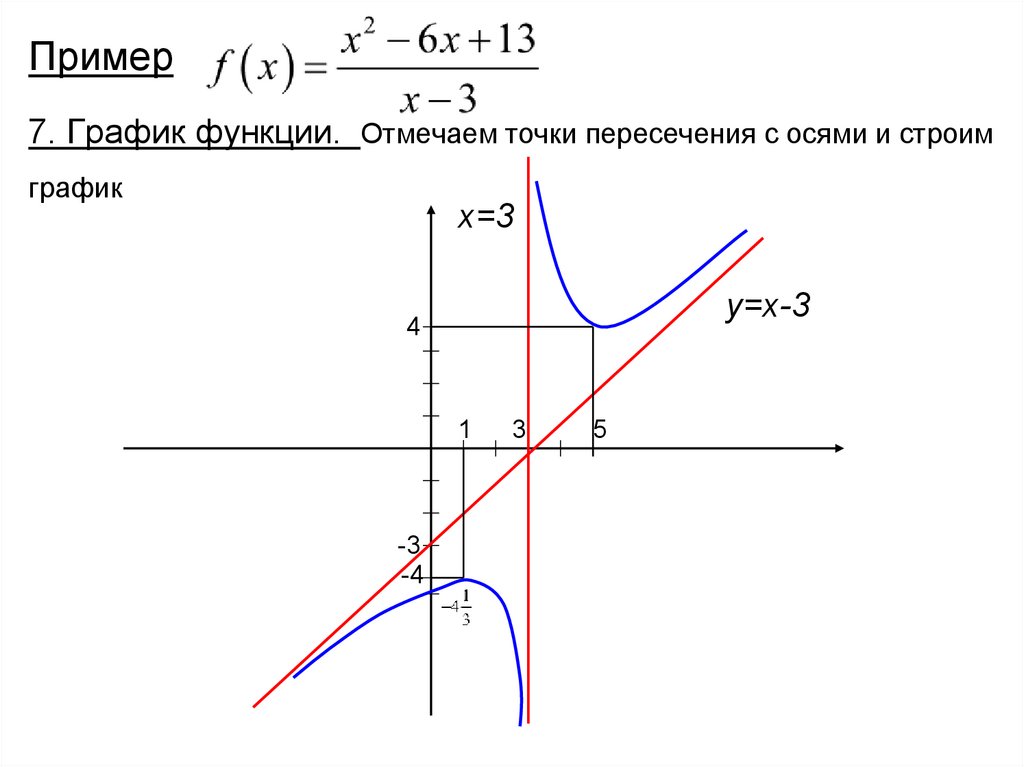
Пример7. График функции. Отмечаем точки пересечения с осями и строим
график
x=3
y=x-3
4
1
-3
-4
3
5



































 Математика
Математика








