Асимптоты графика функции

1.

Асимптотой графика функции y=f(x)
называется прямая, такая что
расстояние от точки (x,f(x)) до этой
прямой стремиться к нулю при
неограниченном удалении точек графика
от начала координат.

2.

y
y f (x)
x

3.

y
y f (x)
x

4.

y
y f (x)
x

5.

Пусть функция y=f(x) определена в
некоторой окрестности точки х0
(исключая, может быть, саму эту
точку) и хотя бы один из пределов
функции при
x x0 0
или
x x0 0
(слева )
(справа )
равен бесконечности, т.е.

6.

lim f ( x)
x x0 0
или
lim f ( x)
x x0 0
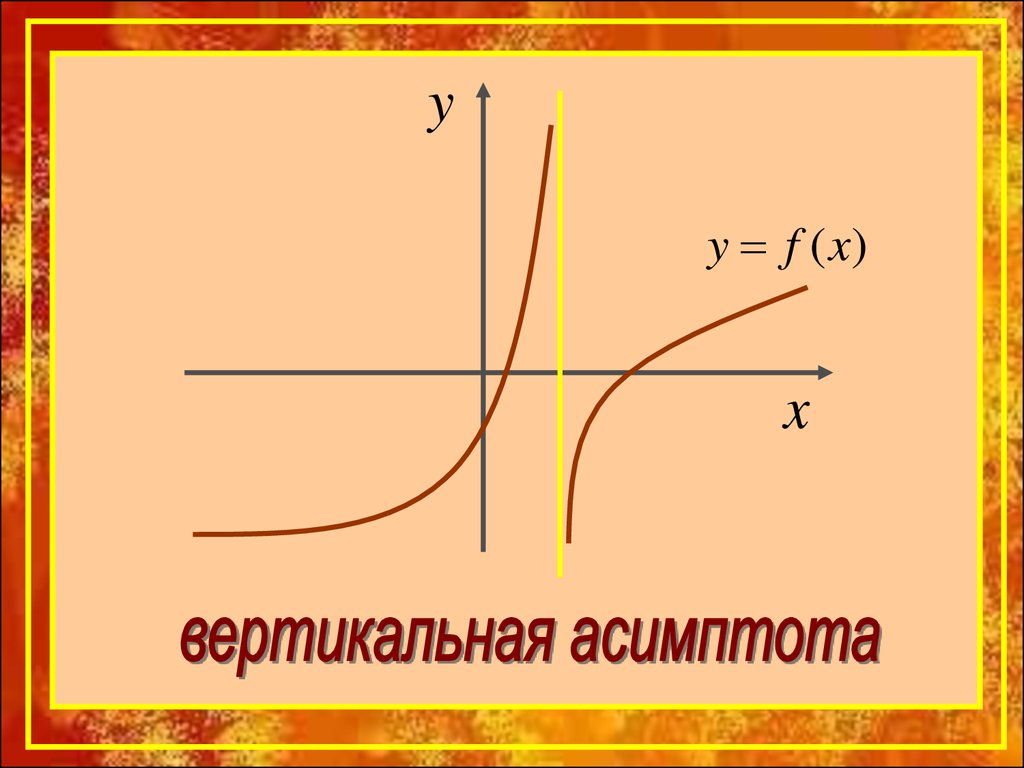
Тогда прямая х=х0 является
вертикальной асимптотой графика
функции y=f(x).

7.

Очевидно, что прямая х=х0 не может быть
вертикальной
асимптотой,
если
функция
непрерывна в точке х0, т.к. в этом случае
lim f ( x) f ( x0 )
x x0
Следовательно, вертикальные асимптоты х=х0
следует искать в точках разрыва функции y=f(x)
или на концах ее области определения (a,b),
если a и b – конечные числа.

8.

Пусть функция y=f(x) определена при
достаточно больших х и существует
конечный предел функции
lim f ( x) b
x
Тогда прямая y=b является
горизонтальной асимптотой
графика функции y=f(x).

9.

Пусть функция y=f(x) определена при
достаточно больших х и
существуют конечные пределы
f ( x)
lim
k
x
x
lim f ( x) k x b
x
Тогда прямая y=kx+b является
наклонной асимптотой графика
функции y=f(x).

10.

Найти асимптоты графика функции
3
x
y 2
x 1

11.

1
2
Функция
не
имеет
точек
разрыва,
следовательно вертикальных асимптот у нее
нет.
Найдем горизонтальные асимптоты:
3
x
lim 2
x
x 1
Предел равен бесконечности,
горизонтальных асимптот нет.
3
следовательно
Найдем наклонные асимптоты:

12.

f ( x)
x3
x2
lim
lim 2 : x lim 2
1
x
x
x
x
x 1
x 1
k 1
x3
lim f ( x) kx lim 2
x
x
x x 1
x x x
x
lim
lim
0
2
2
x
x
x 1
x 1
3
3
b 0
y x
Следовательно, прямая
является наклонной асимптотой.