Похожие презентации:
Логарифмы. От простого к сложному
1.
Государственное автономное профессиональноеобразовательное учреждение
Краснодарского края
«Брюховецкий многопрофильный техникум»
от простого к сложному
Логарифмы
10 занятий
выполнено студентами 807 группы Донченко А. и Мостовым В., обучающимися по профессии
«Мастер отделочных строительных работ»
2.
ВведениеУважаемый друг!
Перед тобой тренажер по теме «Логарифмы».
Для его прохождения тебе понадобятся базовые знания 7-9
классов: умение выполнять арифметические действия с
целыми числами и десятичными дробями, умение вычислять
несложные степени, умение вычислять корни квадратные,
умение решать квадратные уравнения.
Если что-то из этого вызовет затруднения, на страницах есть
подсказки. Тренажер состоит из 10 занятий, каждое занятие
необходимо постараться выполнить за 20 минут. Эти занятия
помогут тебе справится с заданиями 5 и 9 первой части ЕГЭ,
содержащими логарифмы.
Хочется сказать, что этот тренажер – всего лишь первый шаг
в освоении темы «Логарифмы». Он придаст тебе уверенности,
что логарифмы – посильная задача для тебя.
3.
Занятие 1. Вычисление логарифма по определениюЕсли ты не помнишь степени:
20= 21=
22=
23=
24=
1
2
4
8
16
30=1
31=3
32=9
33=
27
34=
81
5
6
2=
32
2=
64
35=
243
36=
729
7
8
2=
128
2=
256
9
2=
512
Отрицательные степени
и
2-1=
2-3=
2-2=
т.д.
3-1=
3-2=
3-3=
и
т.д.
40=1 41=4
42=16
43=64 44=256
4-1=
4-2=
4-3=
и
т.д.
50=1 51=5
52=25
53=125 54=625
5-1=
5-2=
5-3=
и
т.д.
60=1 61=6
62=36
63=216
6-1=
6-2=
6-3=
и
т.д.
70=1 71=7
72=49
73=343
7-1=
7-2=
7-3=
и
т.д.
80=1 81=8
82=64
83=512
8-1=
8-2=
8-3=
и
т.д.
90=1 91=9
92=81
93=729
9-1=
9-2=
9-3=
и
т.д.
10-1=
10-2=
10-3=
0,1
=0,01
=0,001
и
т.д.
100=1 101=10 102=100
112
121
122
144
132
169
142
196
152
225
162
256
172
289
182
324
192
361
202
400
!!Пользуйся этой таблицей для вычисления логарифмов
И еще выучи дробные степени:
,
,
,
и т.д
,
(допиши сам)
Определение логарифма:
Изучаем:
степень
Логарифм = степень
степень
23
аргумент
основание
основание
Обрати внимание:
в степени двойка
находится внизу под
тройкой
и в логарифме двойка
находится внизу!!
!!Потрать на осознание этого пару минут, иначе ничего не получится
2
(два в пятой степени 32)
Закрепляем:
пользуемся таблицей степеней
1
4.
Отрабатываем:смотрим в таблицу степени 3-ки,
видим, что 81 это четвертая степень 3-ки, значит
1. Заполни клеточки:
34 = 81
25 = 32
62 = 36
6-2 =
7-3 =
9-1 =
2. Вычисли логарифмы:
52 = 25
10-2 =
= 0,01
пользуемся таблицей степеней
Последний логарифм
записывается по другому:
= lg 1000 и называется десятичный логарифм
Отрабатываем:
lg 1000 = ⬚
например lg 10 = 1
lg 100 = ⬚
1. Вычисли логарифмы:
пользуемся таблицей степеней 10-и
lg 10000 = ⬚
lg 0,1 = ⬚
пользуемся таблицей отрицательных степеней
5.
Занятие 2. Как из числа сделать логарифм.или
Изучаем:
Закрепляем:
,
, lg 10 = 1
,
тут стоит невидимая 10-ка
Изучаем:
научимся переводить числа в логарифмы с любыми основаниями
Представим число 2 с логарифмами по основаниям 6, 7, .
Для этого выполним следующие действия:
,
,
одинаковые
одинаковые
.
одинаковые
Осталось их только посчитать
,
,
Придумаем логарифмы для 3-ки:
3
3 = lg 10 ,
,
Закрепляем:
, и т.д.
(помним где одинаковые числа)
!!И еще про степени:
Из-за минуса
Из-за минуса
Из-за минуса
Из-за минуса
переворачиваем
переворачиваем
переворачиваем
переворачиваем
и получаем 3
и получаем 4
и получаем 10
и получаем
возводим в 4-ую степень и 1 и 3
6.
Отрабатываем:1. Заполни клеточки:
Решение простейших логарифмических уравнений без определения
Изучаем:
, х
уравнения вида
и
у
разные
одинаковые
числа
решается просто:
х=у
, т.е. отбрасываем логарифмы.
Закрепляем:
х–3=7
х=7⬚3
х=⬚
Ответ: ⬚
Отрабатываем:
2. Заполни клеточки:
х+⬚=⬚
⬚ – ⬚ = 11
15 – ⬚ = ⬚
х=⬚–⬚
⬚ = 11 ⬚ ⬚
–⬚ = ⬚ – 15
х=⬚
⬚=⬚
х=⬚
Ответ: ⬚
Ответ: ⬚
Ответ: ⬚
7.
Занятие 3. Решение простейших уравнений по определению.Изучаем:
если ты видишь уравнение такого вида:
логарифм = число
например
и если в основании логарифма (внизу) стоит число, а иксы только в аргументе,
то решаем по определению логарифма:
Формула:
x=
Закрепляем:
, и всѐ.
(пользуемся таблицей степеней из Занятия 1)
–х =
х =
х=
2х =
х=⬚
⬚=
х=⬚:2
–х =
Ответ: ⬚
Ответ:
х=⬚
х=–
Ответ: ⬚
Ответ: –
=⬚
Отрабатываем:
1. Заполни клеточки:
4–х =
=⬚
х+7 =
–х=⬚–4
⬚=
х=–⬚
Ответ: ⬚
х+4 =
=⬚
х–4 =
=⬚
х=⬚–4
х=
х = –⬚
х=⬚
х=⬚
Ответ:
Ответ: ⬚
Ответ: ⬚
–7
+4
8.
2. Реши уравнения:–⬚х+⬚ =
=⬚
–⬚х–⬚ =
=⬚
⬚–⬚=
=⬚
–⬚х = ⬚ – ⬚=⬚
–⬚х =⬚ + 14=⬚
–4х = ⬚ – 12
х = ⬚:(– ⬚)
х =⬚:(– ⬚)
х = ⬚:(–4)
х=–⬚
х =–⬚
х =–⬚
Ответ: – ⬚
Ответ:
Ответ: –⬚
–⬚+⬚х = =⬚
⬚х = ⬚ + ⬚=⬚
⬚х+⬚ =
⬚х =⬚ – ⬚=⬚
⬚ + ⬚ х=
=⬚
2х = ⬚ – 10=⬚
х = ⬚: ⬚
х =⬚ : ⬚
х = ⬚:2
х= ⬚
х =⬚
х =⬚
Ответ:
Ответ: ⬚
Ответ:
⬚
=⬚
lg (х+11) = 1
х2–15х =
=⬚
х2–15х–⬚=0
с помощью дискриминанта
или по теореме Виета
находим два корня
х1 = –1,
Ответ:
х2 =16
⬚, ⬚
х+⬚ =
=⬚
lg (–5х+2) = –1
–⬚х+2=
= =0,1
х =⬚ – ⬚= –⬚
–⬚х = 0,1 – 2= –⬚
х=–⬚
х = – ⬚:(–⬚)
Ответ: –
х =⬚
Ответ: ⬚
9.
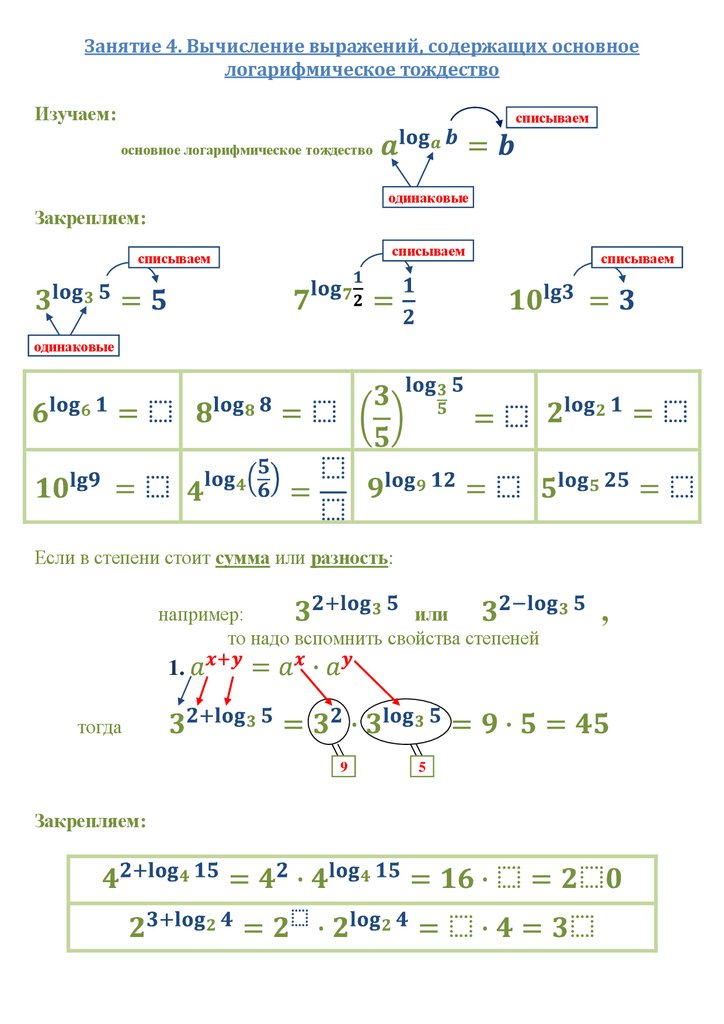
Занятие 4. Вычисление выражений, содержащих основноелогарифмическое тождество
Изучаем:
списываем
основное логарифмическое тождество
одинаковые
Закрепляем:
списываем
списываем
списываем
одинаковые
Если в степени стоит сумма или разность:
например:
или
то надо вспомнить свойства степеней
1.
тогда
9
Закрепляем:
5
,
10.
2.тогда
9
Закрепляем:
Отрабатываем:
1. Заполни клеточки:
5
11.
Занятие 5. Два свойства логарифмовпри вычислении выражений
замечание: далее мы будем рассматривать логарифмы в которых
аргумент и основание – положительные числа
Изучаем:
1-е свойство:
одинаковые
Например:
Закрепляем:
2-е свойство:
–
одинаковые
Например:
смотрим в таблицу
степеней
Закрепляем:
12.
Отрабатываем:1. Заполни клеточки:
(можешь посчитать с помощью калькулятора, но лучше в столбик на черновике )
13.
Занятие 6. Два свойства логарифмовпри решении простейших логарифмических уравнений
Изучаем:
БУДЕТ 2 ТИПА УРАВНЕНИЙ
1. Если х стоит только с одной стороны уравнения:
справа по формуле
делаем деление
дальше как в Занятии 3
решаем простейшее уравнение
2. Если х есть с двух сторон уравнения:
справа по формуле
делаем умножение
дальше как в Занятии 3
решаем простейшее уравнение
и вот здесь надо сделать или проверку или найти ОДЗ
в таких простых уравнениях легче сделать проверку:
там, где есть
х должно быть положительное число:
1. –2+6=4
2. –2+3=1
Оба выражения положительные, значит
–
является корнем.
14.
Отрабатываем:1. Заполни клеточки:
х= ⬚
х =⬚
х =⬚
Ответ: ⬚
Ответ:
Ответ: ⬚
–
–
=
проверка:
1)
проверка:
2)
-7
Ответ:
2)
Ответ:
х= ⬚
х =3
Ответ: ⬚
Ответ:
Ответ: ⬚
15.
Занятие 7. Переход к новому основанию логарифмаИзучаем:
вверху
Эту формулу
используют как
слева направо,
так и справа
налево
логарифмы в числителе и
знаменателе имеют
одинаковые основания
внизу
Закрепляем:
(используй дробные степени под таблицей
степеней в Занятии 1)
Ещѐ:
смотрим по
таблице 2-ки
Закрепляем:
16.
Отрабатываем:1. Заполни клеточки:
2. Заполни клеточки:
(здесь нужно сначала упростить дробь, а затем выполнить сложение, как в Занятии 5)
17.
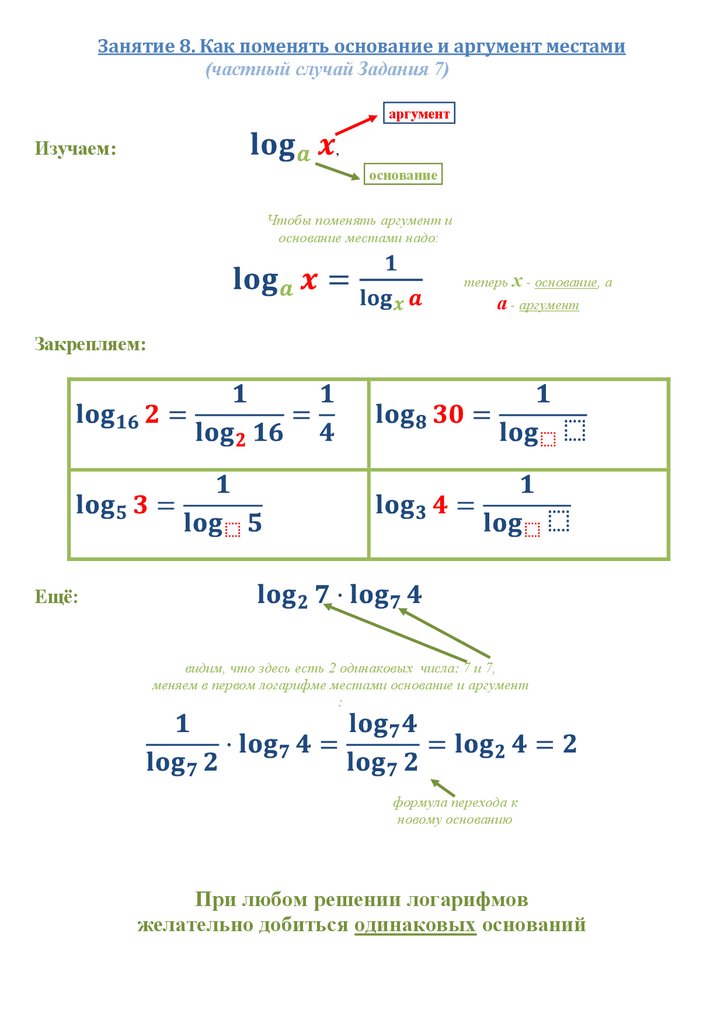
Занятие 8. Как поменять основание и аргумент местами(частный случай Задания 7)
аргумент
Изучаем:
,
основание
Чтобы поменять аргумент и
основание местами надо:
теперь х - основание, а
а - аргумент
Закрепляем:
Ещѐ:
видим, что здесь есть 2 одинаковых числа: 7 и 7,
меняем в первом логарифме местами основание и аргумент
:
формула перехода к
новому основанию
При любом решении логарифмов
желательно добиться одинаковых оснований
18.
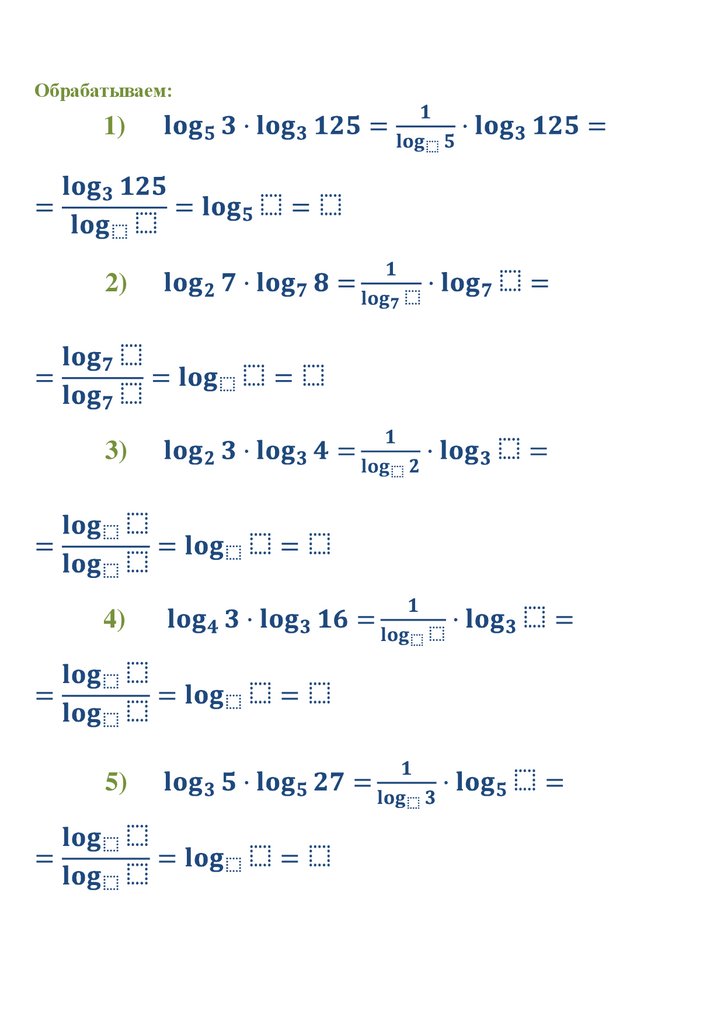
Обрабатываем:1)
2)
3)
4)
5)
19.
Занятие 9. Степени в логарифмеИзучаем:
1. Степень стоит в аргументе
,
степень выносим перед
логарифмом
Усложним: если
– четное, то
Можно использовать и в обратную сторону:
2. Степень стоит в основании
,
степень выносим перед
логарифмом
Закрепляем:
Занести число в логарифм:
Вынести число из логарифма:
Изучаем:
20.
Закрепляем:Заполни клеточки:
Обрабатываем:
!! Если х стоит только с одной стороны уравнения,
то проверку делать не надо
1. Решить уравнения:
Используем Занятие 6.
=⬚
–⬚x = ⬚–⬚
=⬚:(–⬚)=–⬚
Ответ: –⬚
=⬚:(–⬚)=–⬚
Ответ:–
Ответ: –⬚
Ответ:
Ответ: ⬚
2. Решить уравнения:
выносим
перед логарифмом, а
27 представляем степенью 3-ки
выносим
перед логарифмом
равно 1
=⬚
=⬚
Ответ: ⬚
21.
Занятие 10. «Фишечки»Изучаем:
Есть свойства, которых нет в учебнике, но они очень упрощают решение.
1-е свойство:
Например:
Закрепляем:
решим примеры из Занятия 8 по этому свойству
Как видно, по этому свойству решать намного проще
2-е свойство:
Например:
Закрепляем:
решим примеры из Занятия 9 по этому свойству
=
=⬚
=
Рассмотрим некоторые примеры на вид сложные, но они решаются очень просто











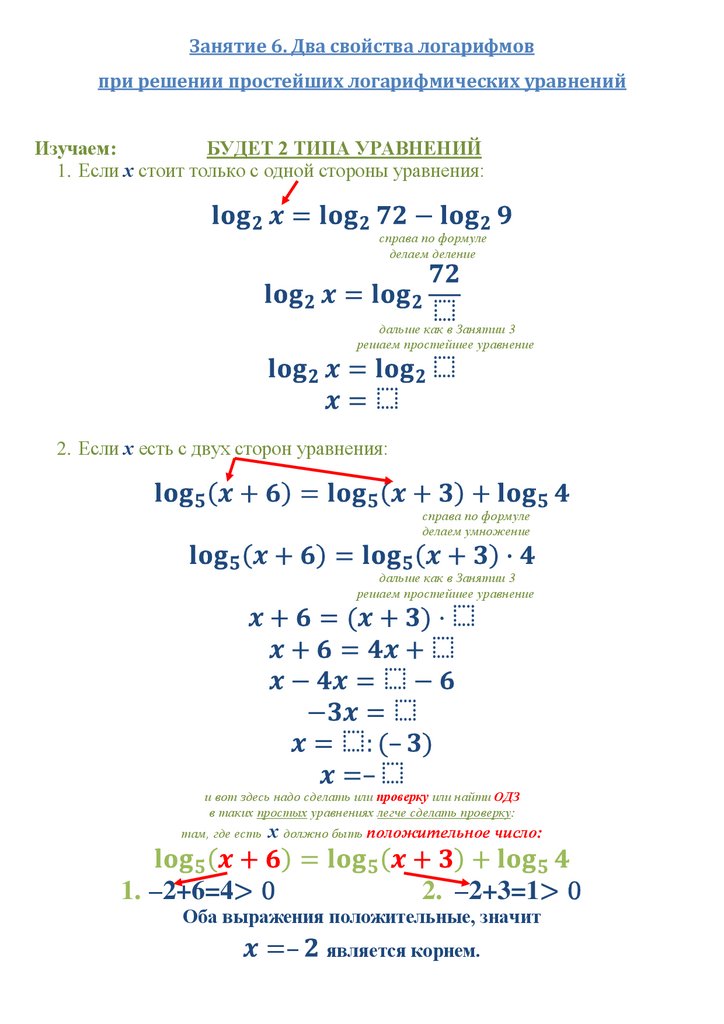






 Математика
Математика








