Площадь трапеции (От простого к сложному)

1.

(От простого к сложному)
Петухова Ирина Валентиновна, учитель МБОУ СОШ №4,
Г. Полярные Зори Мурманской области.

2.

Цели и задачи урока:
Повторить свойства площадей фигур; свойство
медианы треугольника; свойство площадей
треугольников, имеющих одинаковую высоту;
Свойство площадей подобных фигур.
Развивать умения анализировать, сопоставлять,
логически
мыслить,
обобщать;
развивать
внимание,
память,
активность
и
самостоятельность.
Воспитывать
ответственное
отношение
к
учебному труду, настойчивость для достижения
конечного результата, умение работать в
коллективе.

3.

Отношение площадей подобных треугольников
равно квадрату коэффициента подобия.
B
F
A
ABC подобен FBK .
K
BA k BF .
S ABC
1
BA BC sin B.
2
S FBK
1
BF BK sin B.
2
C
S ABC
BA BC
S FBK
BF BK
k k
k
2

4.

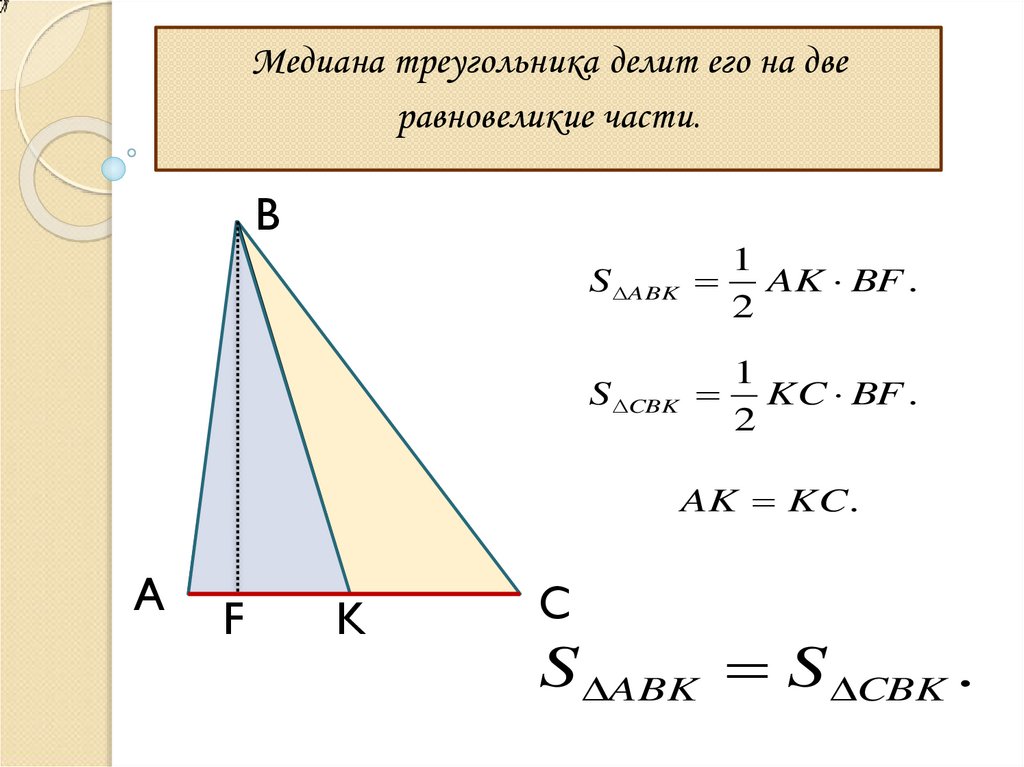
Медиана треугольника делит его на две
равновеликие части.
B
S ABK
1
AK BF .
2
S CBK
1
KC BF .
2
AK KC.
A
F
K
C
S ABK S CBK .

5.

Задачка : В прямоугольном треугольнике АВС точка О –
середина медианы СН, проведенной к гипотенузе АВ, АС = 6см,
ВС = 8см. Найдите площадь треугольника ОВС.
Т .к. АН ВН , то S CBH
А
Т .к. OН OC , то S CBO
Н
S CBO
О
С
В
1
S ABC .
2
1
S HBC .
2
1
S ABC .
4
1
1
S ABC ab 6 8 24(см 2 ).
2
2
1
S CBO 24 6(см 2 ).
4
Ответ : 6см 2 .

6.

Если два треугольника имеют одинаковые высоты, то отношение
их площадей равно отношению длин оснований (сторон, на
которые опущены эти высоты).
B
S CBK
S ABK
1
KC BF .
2
1
AK BF .
2
S CBK
KC
AK
S ABK
A F K
C

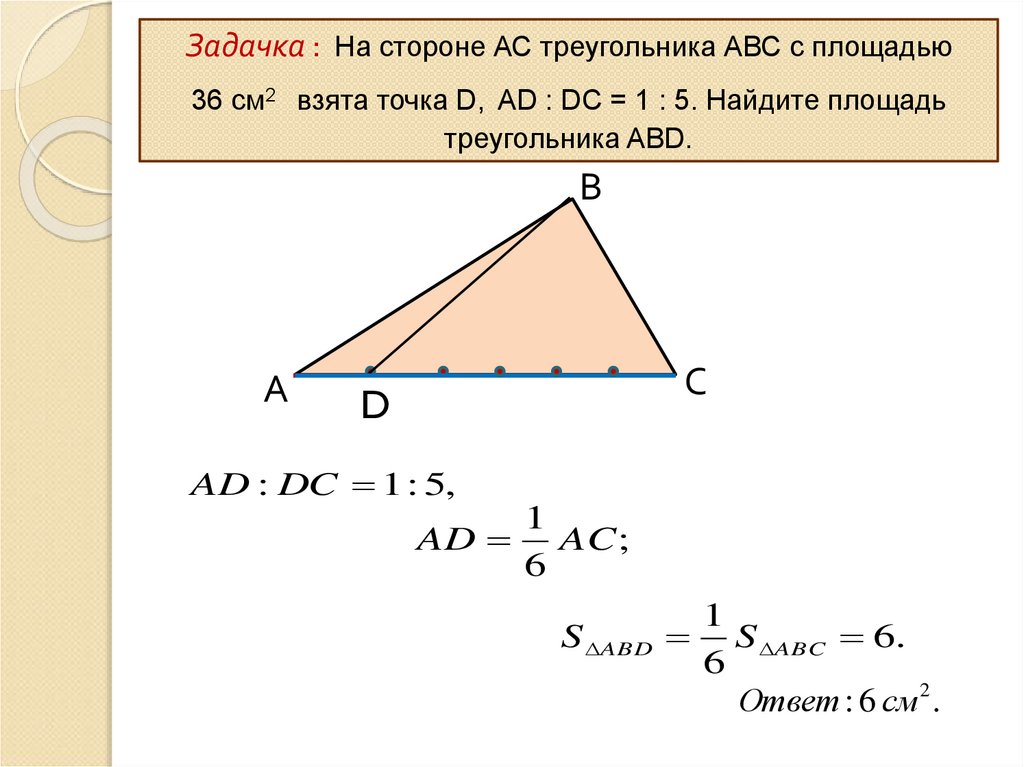
7.

Задачка : На стороне АС треугольника АВС с площадью
36 см2 взята точка D, AD : DC = 1 : 5. Найдите площадь
треугольника ABD.
В
А
С
D
AD : DC 1 : 5,
1
AD AC ;
6
S ABD
1
S ABC 6.
6
Ответ : 6 см2 .

8.

Задачка :В ромбе ABCD диагонали равны 5 см и 12 см.
На диагонали АС взята точка М так, что АМ : МС = 4 : 1.
Найдите площадь треугольника AMD.
D
S CDA
S MDA
С
1
S ABCD
2
4
S CDA
5
4 1
2
S ABCD S ABCD ,
5 2
5
1
1
S ABCD d1d 2 5 12 30,
2
2
2
S MDA 30 12.
5
А S MDA
M
В
Ответ : 12см 2 .

9.

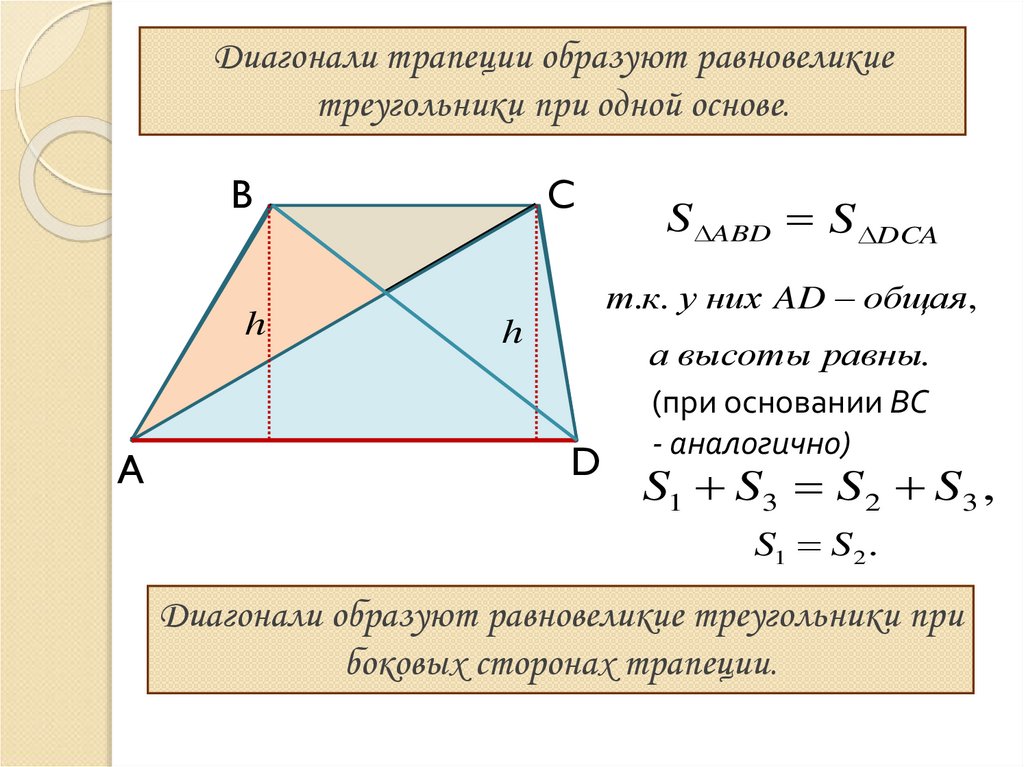
Диагонали трапеции образуют равновеликие
треугольники при одной основе.
B
C
S1
S2
h
т.к. у них AD общая,
h
S3
A
S ABD S DCA
D
а высоты равны.
(при основании ВС
- аналогично)
S1 S3 S 2 S3 ,
S1 S2 .
Диагонали образуют равновеликие треугольники при
боковых сторонах трапеции.

10.

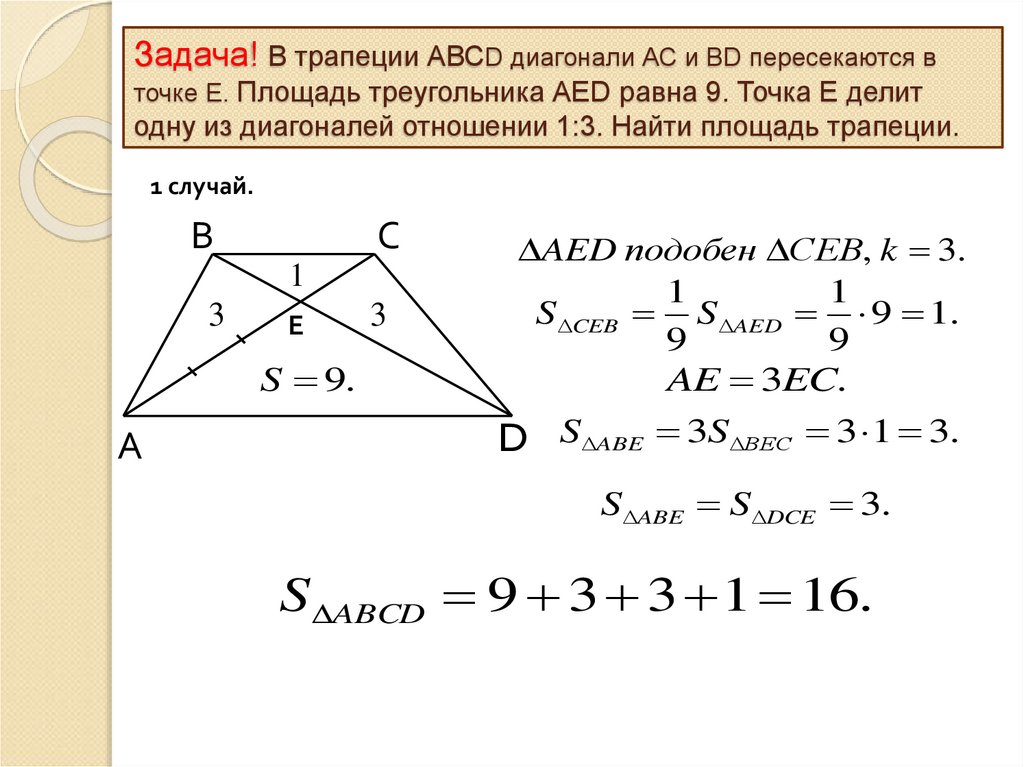
Задача! В трапеции АВСD диагонали АС и ВD пересекаются в
точке Е. Площадь треугольника АЕD равна 9. Точка Е делит
одну из диагоналей отношении 1:3. Найти площадь трапеции.
1 случай.
В
С
1
3
Е
S 9.
А
3
AED подобен СЕВ, k 3.
1
1
S CEB S AED 9 1.
9
9
AE 3EC.
D S ABE 3S ВЕС 3 1 3.
S ABE S DCE 3.
S ABCD 9 3 3 1 16.

11.

Задача! В трапеции АВСD диагонали АС и ВD пересекаются в
точке Е. Площадь треугольника АЕD равна 9. Точка Е делит
одну из диагоналей отношении 1:3. Найти площадь трапеции.
S AED S BEC 9.
2 случай.
А
В
3
S 9. Е
DE 3BE.
9
27
D
S AEB
С
1
1
S AED 9 3.
3
3
DEC подобен AЕВ, k 3.
S DEC 9S AEB 9 3 27.
S ABCD 9 9 3 27 48.

12.

Задача! В трапеции АВСD диагонали АС и ВD пересекаются в
точке Е. Площадь треугольника АЕD равна 9. Точка Е делит
одну из диагоналей отношении 1:3. Найти площадь трапеции.
3 случай.
D
S 9.
27
Е
А
BEC подобен DЕA, k 3.
27
S CEB 9S AED 9 9 81.
81
С
В
S CED 3S AED 3 9 27.
S CED S BEA 27.
S ABCD 9 81 27 27 144.
Ответ : 16; 48; 144.

13. Литература :

1. Корянов А.Г. Математика ЕГЭ.- Г.Брянск, 2010.
2. Гордин Р.К. ЕГЭ 2011. Математика. Задача С4.М.Издательство МЦНМО, 2011.
3. Атанасян Л.С. Геометрия 7-9.-М.Просвещение,
2006.
4. Гаврилова Н.Ф. Поурочные разработки по
геометрии (дифференцированный подход).-М.
ВАКО, 2005