Похожие презентации:
Диференціальне числення. Похідна функції (лекція 1.2)
1. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
Лекція 1.22. Похідна функції
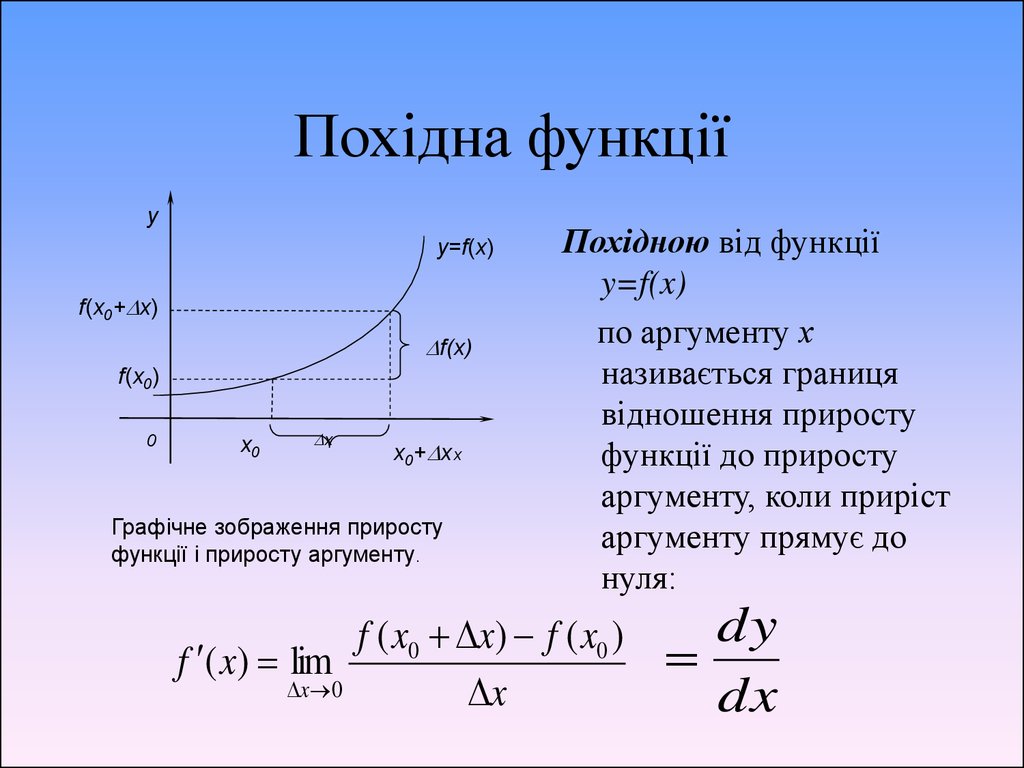
yy=f(x)
f(x0+ x)
f(x)
f(x0)
0
x0
x
x0+ x x
Графічне зображення приросту
функції і приросту аргументу.
Похідною від функції
y=f(x)
по аргументу х
називається границя
відношення приросту
функції до приросту
аргументу, коли приріст
аргументу прямує до
нуля:
f ( x0 x) f ( x0 )
f ( x) lim
x 0
x
dy
dx
3. Алгоритм знаходження похідної
1) y f ( x) f ( x0 x) f ( x0 )у
2)
х
у
3) y lim
x 0 х
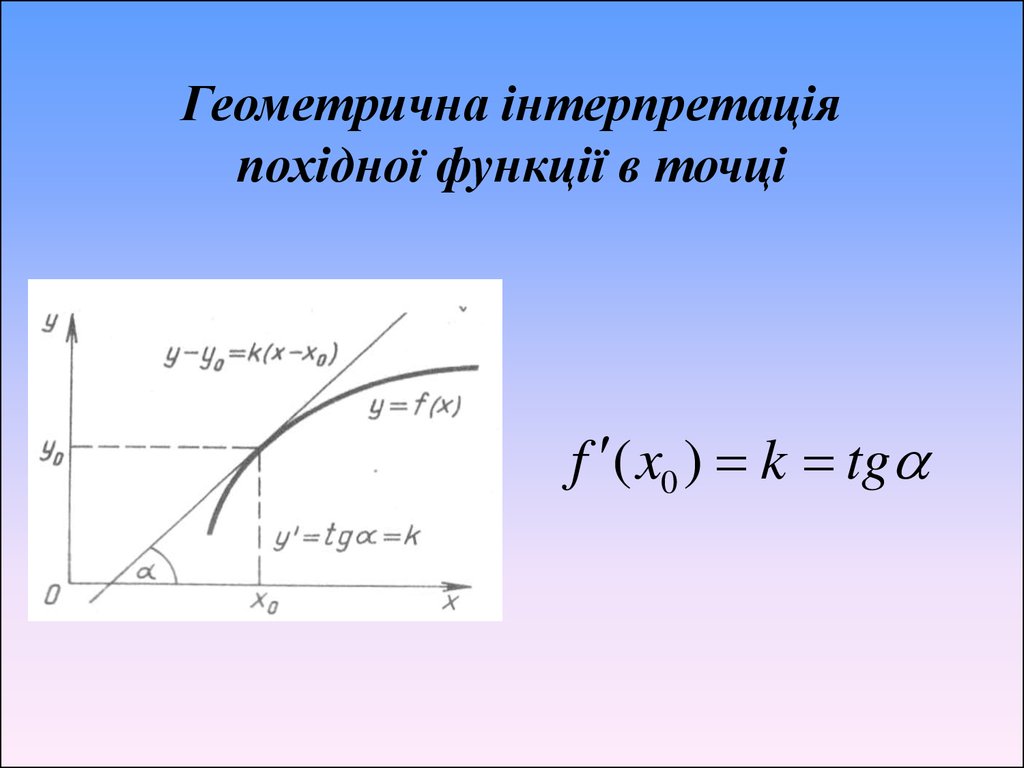
4. Геометрична інтерпретація похідної функції в точці
f ( x0 ) k tg5.
f ( x0 ) k tg• Геометричний зміст похідної
полягає у тому, що значення похідної
функції y=f(x) у точці x0 дорівнює
кутовому коефіцієнту дотичної до
графіка функції у точці з абсцисою
x 0:
6. Фізичний зміст похідної функції
y f ( x) S (t )S (t0 ) (t0 ) lim
t 0
S
t
-
миттєва швидкість
S (t0 ) (t0 ) a(t0 ) - прискорення
•Миттєва швидкість прямолінійного руху
дорівнює похідній шляху за часом руху
•Похідна від швидкості по часу(або друга
похідна від шляху) є прискоренням
7. Правила диференціювання
(u ) u- похідна алгебраїчної
суми функції;
(u ) u u
- похідна добутку функції;
u u u - похідна від частки
2
функцій.
8. Таблиця знаходження похідних елементарних функцій
9. Таблиця знаходження похідних елементарних функцій
10. Приклади визначення похідної функції
№1( y) ( x 2 sin x) ( x 2 ) (sin x) 2 x cos x
№2
1
1
( y ) ( x ln x) ( x ) ln x (ln x) x
ln x x
x
2 x
№3
( y) (
x
( x) cos x (cos x) x 1 cos x ( sin x) x cos x x sin x
)
2
2
cos x
cos x
cos x
cos2 x
11. Диференціювання складених функцій
12. Диференціювання складених функцій
y sin 2 x,- складена функція
y sin u ( x), u ( x) 2 x,
y f (u ( x))
- загальний вигляд
складеної функції, де
- проміжний аргумент
u (x)
Похідна складеної функції
( y ) x f (u ( x)) f (u ) u ( x)
13. Таблиця похідних складених функцій
14. Таблиця похідних складених функцій
15. Приклади знаходження похідних складених функцій
№1(cos 4 x) sin 4 x (4 x) 4 sin 4 x
№2
2
2
(cos 4 x) 3 cos 4 x (cos4 x) 12 cos 4 x sin 4 x
3
16. Функція багатьох змінних
S ab• площа прямокутника: (де a і
b- довжини сторін),
V abc
• об’єм паралелепіпеда: (де a і
b - довжини сторін основи, а
c - висота).
S S ( a , b)
• Дані формули задають
функції двох і трьох змінних
V V (a, b, c)
z f ( x, y)
• Функція двох змінних,
представлена у загальному
вигляді
17. Частинні похідні функції багатьох змінних
• Частинна похідна першого порядку функції поаргументу x:
x f
f ( x x; y) f ( x; y) f
lim
lim
f x
x 0 x
x 0
x
x
• Частинна похідна першого порядку функції по
аргументу у:
y f
f ( x; y y ) f ( x; y ) f
lim
lim
f y
y 0 y
y 0
y
y
18. Приклад знаходження частинних похідних
Знайти частинні похідні функції по x i по yz ( x, y ) x 2 4 y 3
z
z x ( x 2 4 y 3 ) x ( x 2 ) x (4 y 3 ) x 2 x 0 2 x
x
z
z y ( x 2 4 y 3 ) y ( x 2 ) y (4 y 3 ) y 0 12 y 2 12 y 2
y
19. ДИФЕРЕНЦІАЛ ФУНКЦІЇ
df f ( x) dxdf d x f d y f , або
f
f
df dx dy
x
y
• Диференціал
функції однієї
змінної
• Повний
диференціал
функції двох
змінних
20. Приклади знаходження диференціала функції
• Знайти диференціал функціїу ln 4 x при x 1, x 0,1
Рішення :
( 4 x)
dy (ln 4 x ) dx
x
4x
4
1
1
x x 0,1 0,1
4x
x
1



















 Математика
Математика








