Похожие презентации:
Комбинации многогранников и тел вращения
1.
«Решение задач на комбинациимногогранников и тел
вращения»
2.
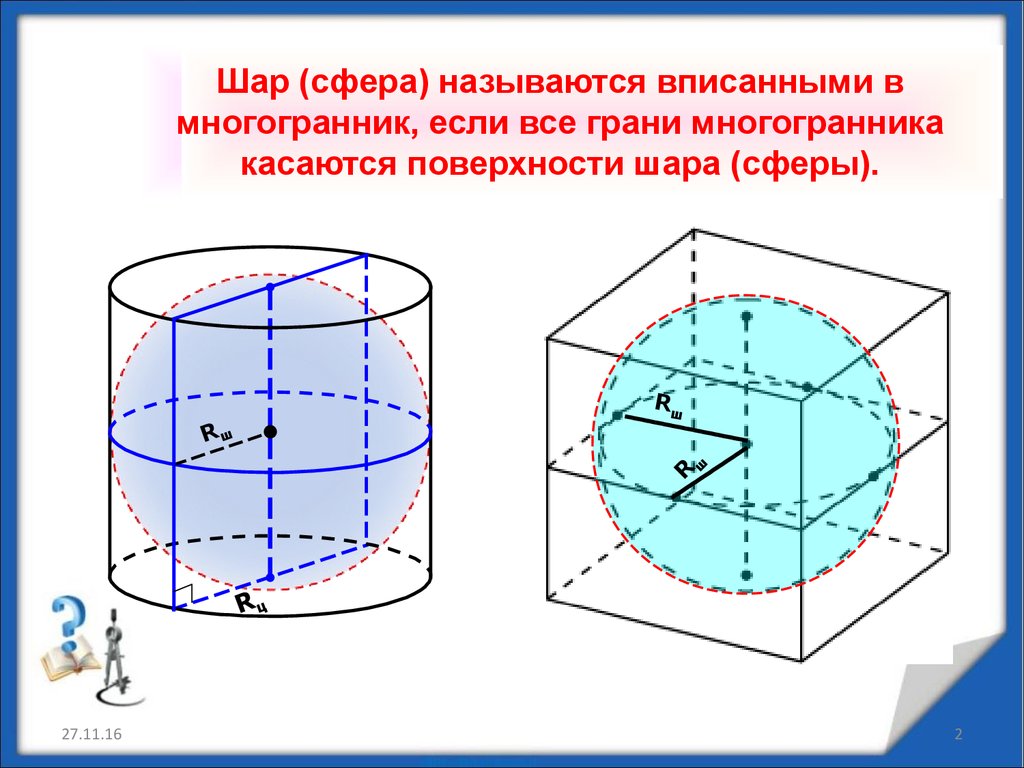
Шар (сфера) называются вписанными вмногогранник, если все грани многогранника
касаются поверхности шара (сферы).
Rш
Rш
Rш
Rц
27.11.16
2
3.
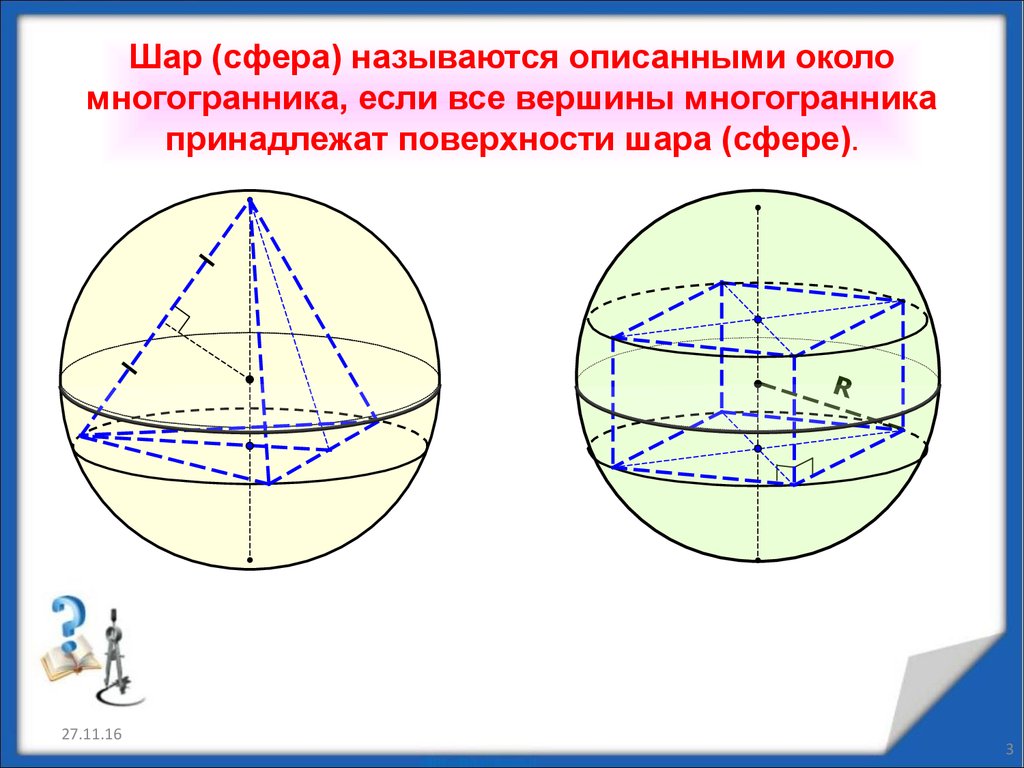
Шар (сфера) называются описанными околомногогранника, если все вершины многогранника
принадлежат поверхности шара (сфере).
R
27.11.16
3
4.
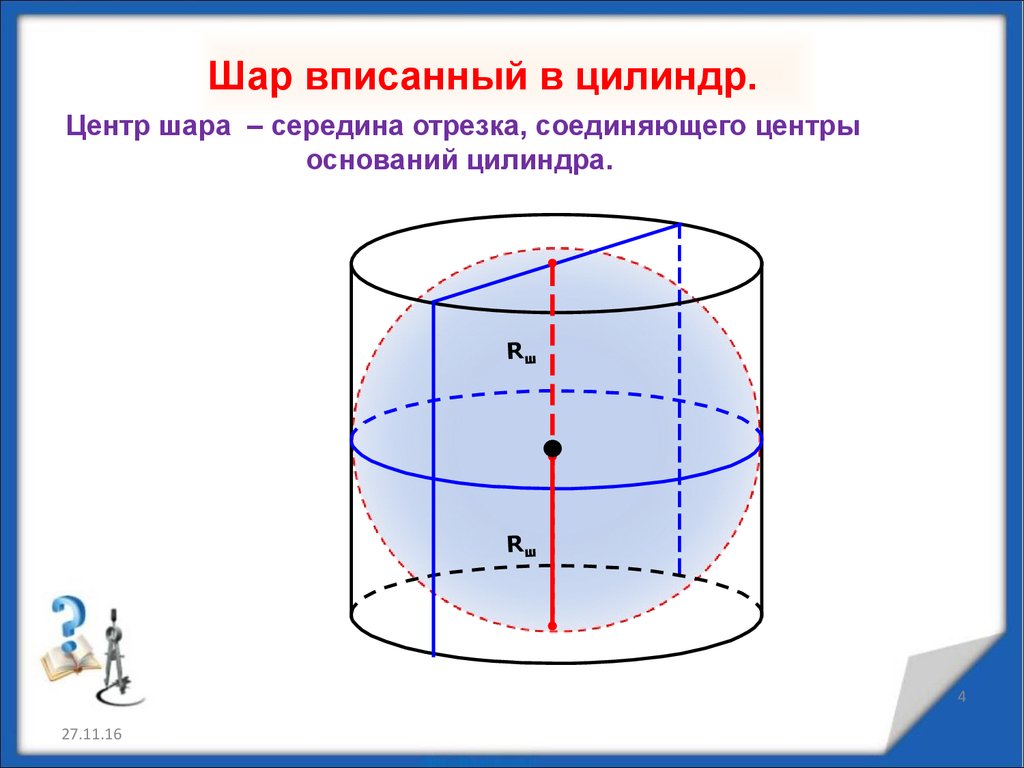
Шар вписанный в цилиндр.Центр шара – середина отрезка, соединяющего центры
оснований цилиндра.
Rш
Rш
4
27.11.16
5.
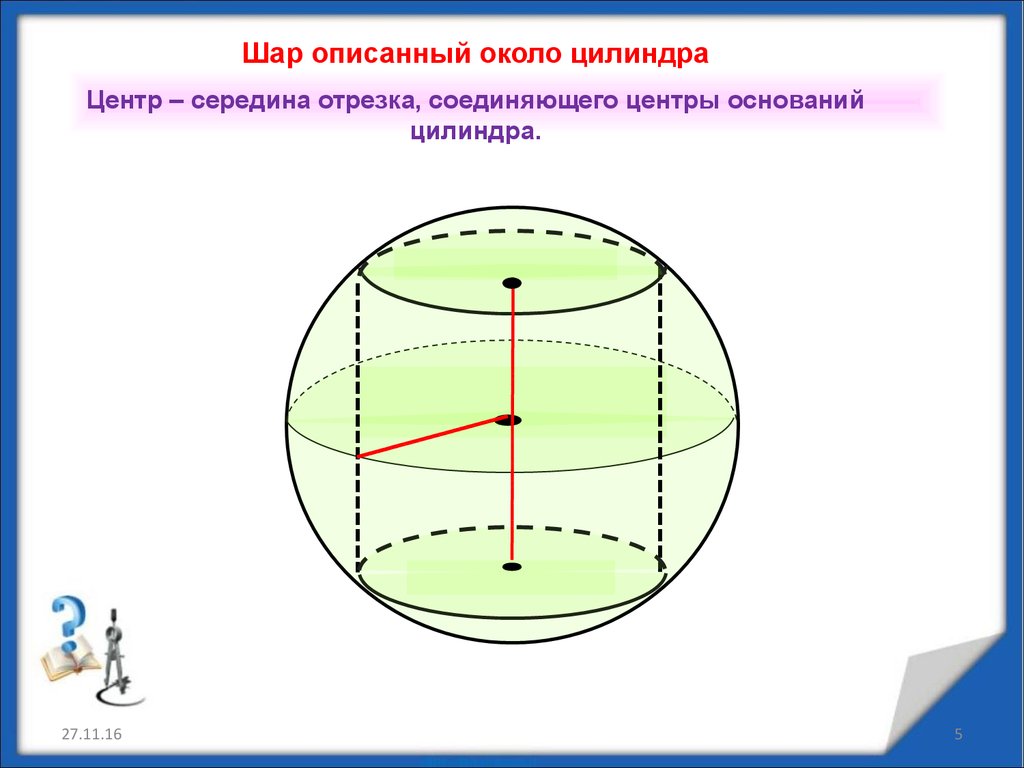
Шар описанный около цилиндраЦентр – середина отрезка, соединяющего центры оснований
цилиндра.
27.11.16
5
6.
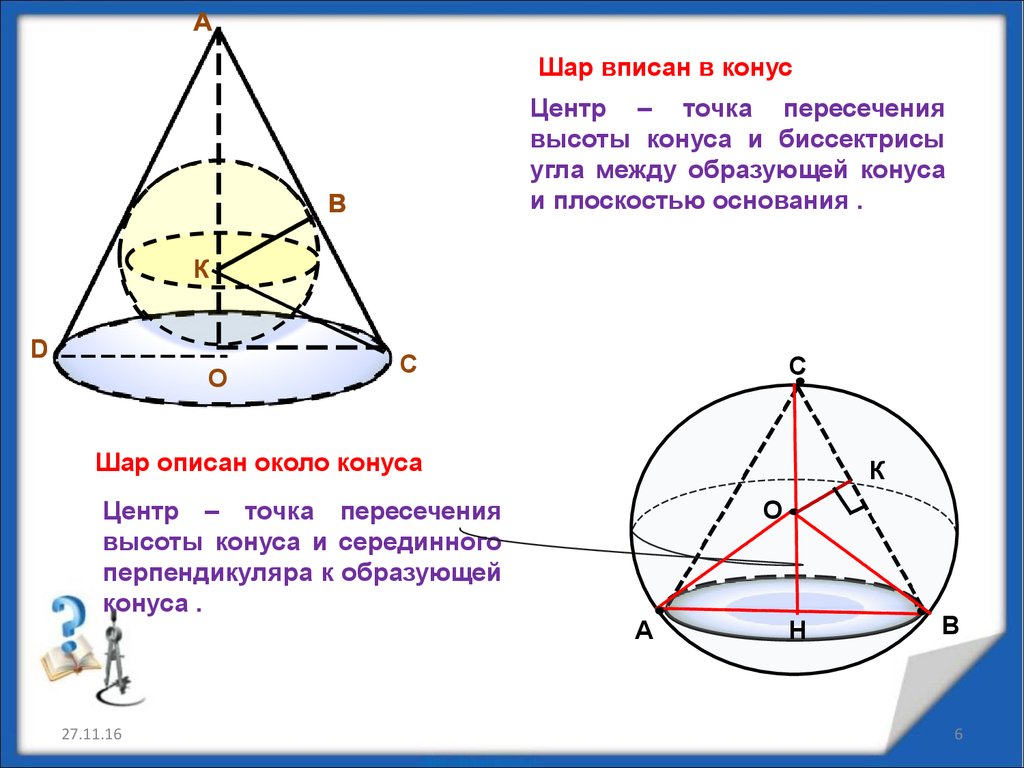
АШар вписан в конус
Центр – точка пересечения
высоты конуса и биссектрисы
угла между образующей конуса
и плоскостью основания .
В
К
D
О
С
С
Шар описан около конуса
Центр – точка пересечения
высоты конуса и серединного
перпендикуляра к образующей
конуса .
27.11.16
К
О
А
Н
В
6
7.
Задачи27.11.16
1
Шар вписанный в конус
2
Шар описанный около конуса
3
Конус вписанный в шар
4
Шар вписанный в цилиндр
5
Шар вписанный в куб
7
8.
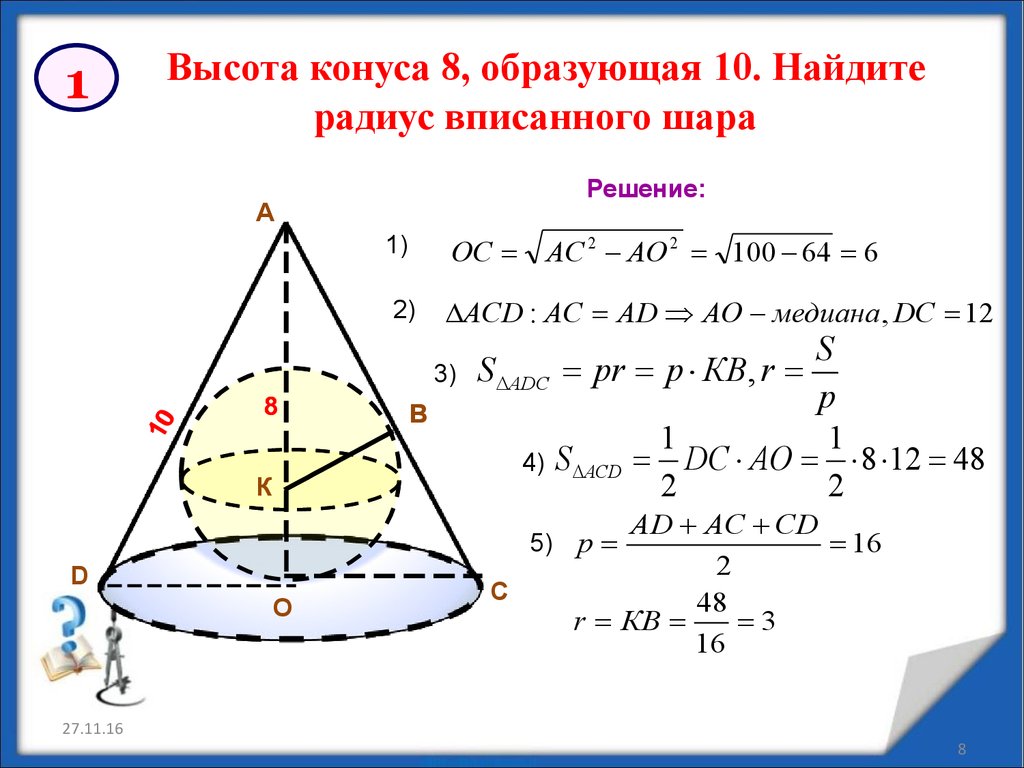
1Высота конуса 8, образующая 10. Найдите
радиус вписанного шара
Решение:
А
1)
ОС
2)
АСD : АС АD АО медиана , DС 12
10
3)
8
К
D
О
27.11.16
В
АС 2 АО 2 100 64 6
S
S ADC рr р КВ, r
р
1
1
4) S ACD DС AO 8 12 48
2
2
AD AC CD
5) p
16
2
С
48
r КВ
3
16
8
9.
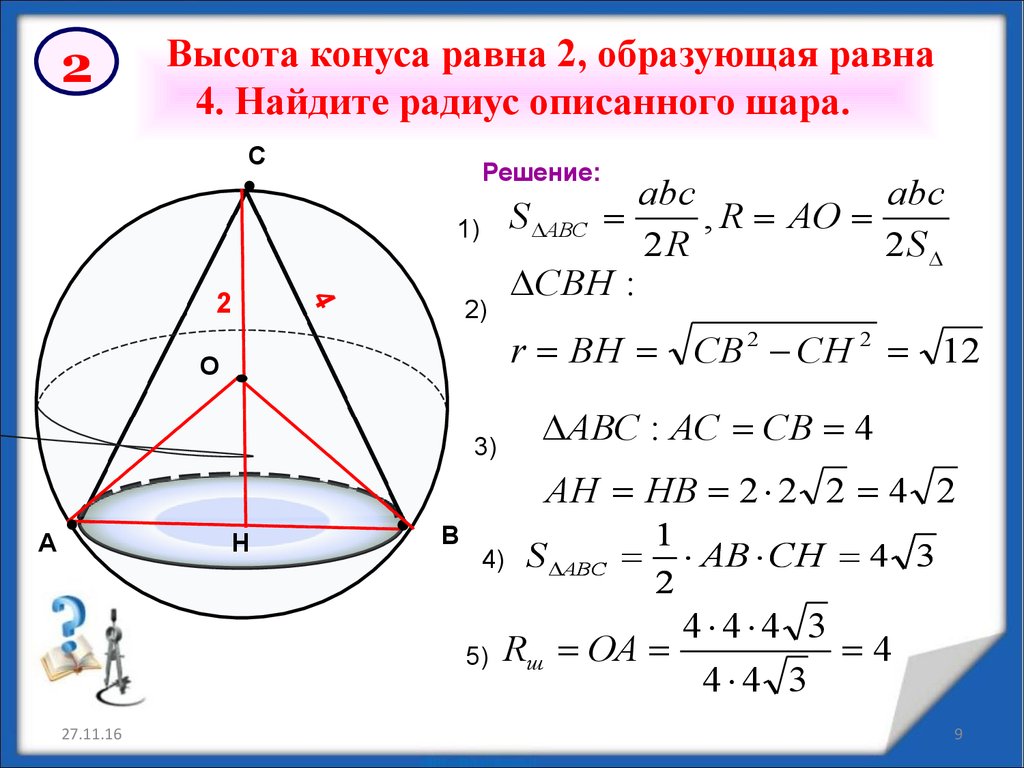
2Высота конуса равна 2, образующая равна
4. Найдите радиус описанного шара.
С
Решение:
abc
abc
S АВС
, R AO
2R
2S
СВН :
1)
2)
4
2
r ВН СВ 2 СН 2 12
О
АВС : АС СВ 4
3)
АН НВ 2 2 2 4 2
А
Н
В
4)
5)
27.11.16
S ABC
1
AB CH 4 3
2
4 4 4 3
Rш ОА
4
4 4 3
9
10.
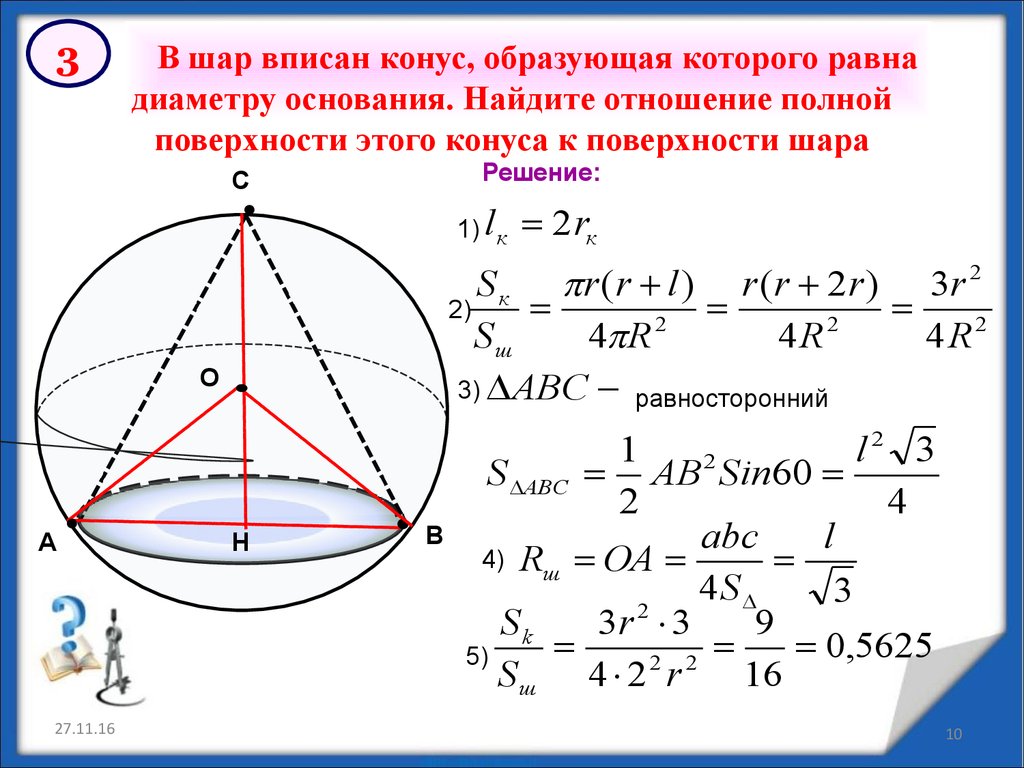
3В шар вписан конус, образующая которого равна
диаметру основания. Найдите отношение полной
поверхности этого конуса к поверхности шара
Решение:
С
1) l к
S к r (r l ) r (r 2r ) 3r 2
2)
2
2
Sш
4 R
4R
4R 2
3) ABC равносторонний
О
А
27.11.16
2rк
Н
В
2
1
l
3
2
S ABC AB Sin60
2
4
abc
l
4) Rш ОА
4S
3
2
Sk
3r 3
9
0,5625
5)
2 2
Sш 4 2 r
16
10
11.
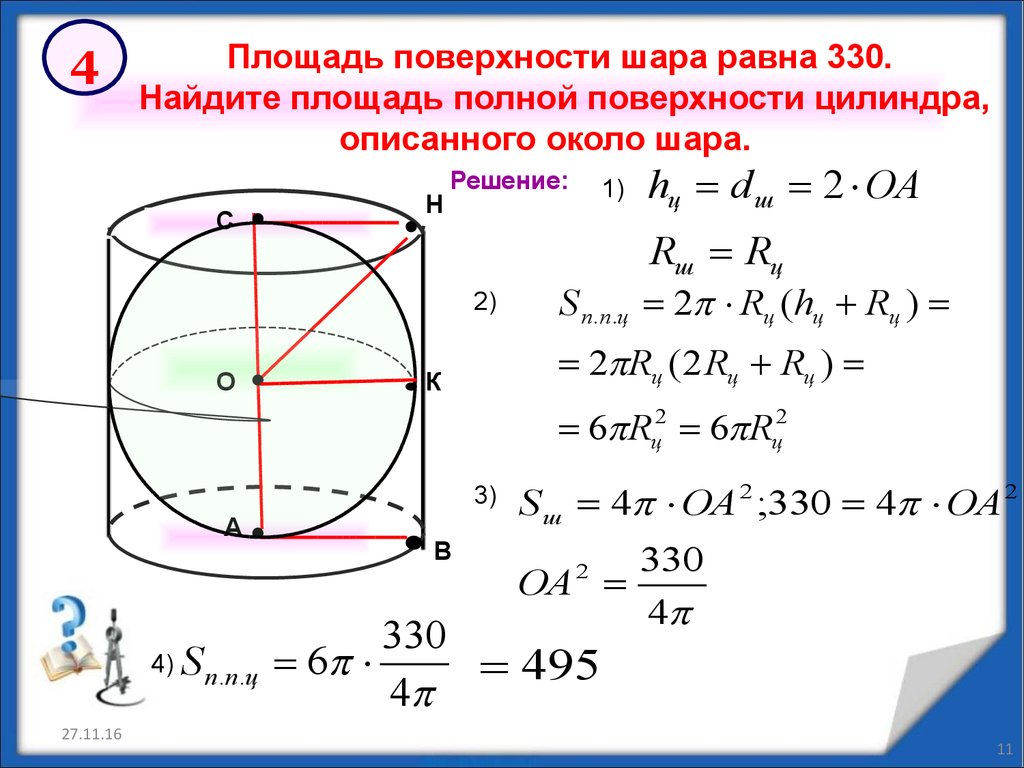
4Площадь поверхности шара равна 330.
Найдите площадь полной поверхности цилиндра,
описанного около шара.
С
Н
Решение:
hц d ш 2 ОА
Rш Rц
2)
О
1)
S п.п.ц 2 Rц (hц Rц )
2 Rц (2 Rц Rц )
К
6 Rц2 6 Rц2
3)
А
4) S п.п.ц
27.11.16
В
S ш 4 ОА 2 ;330 4 ОА 2
330
ОА
4
2
330
6
495
4
11
12.
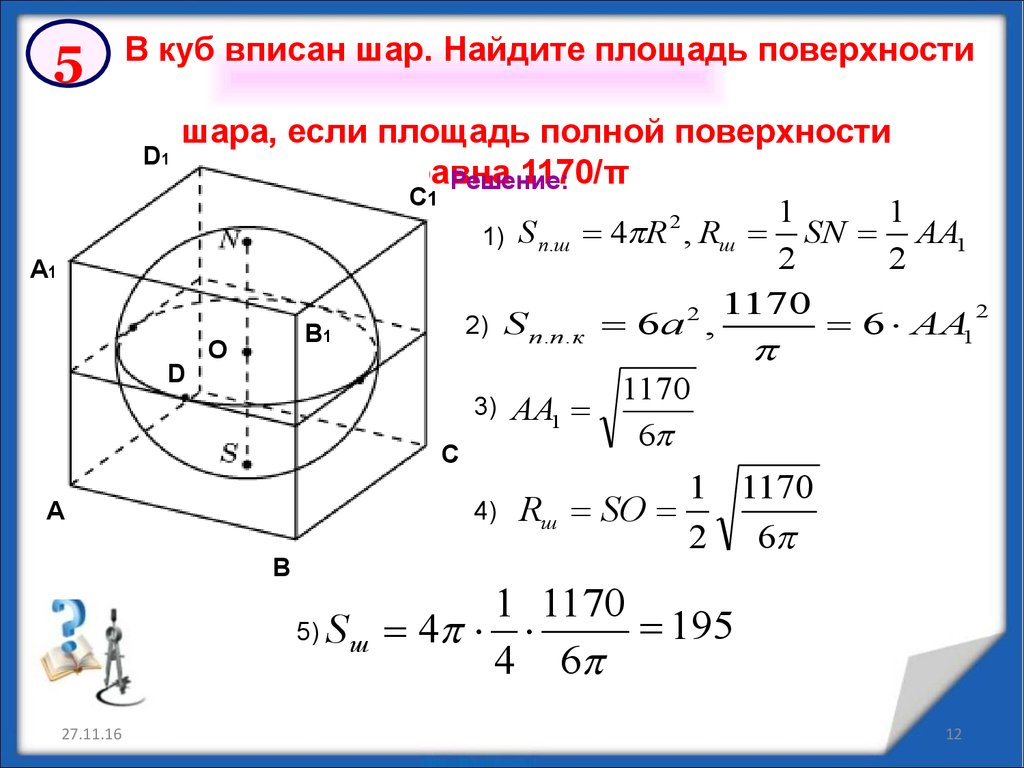
5В куб вписан шар. Найдите площадь поверхности
шара, если площадь полной поверхности
куба равна
1170/π
Решение:
С1
1
1
2
S
4
R
,
R
SN
AA1
1) п.ш
ш
2
2
2
2 1170
2)
S
6
а
,
6
АА
B1
п.п.к
1
О
D
1170
3) АА
1
6
D1
А1
С
А
4)
В
27.11.16
1 1170
Rш SO
2 6
1 1170
195
5) S ш 4
4 6
12
13.
Задачи для самостоятельного решенияНайдите площадь поверхности шара, описанного
около конуса, у которого радиус основания
, а высота
равна
1В. 1
Ответ: 25
Радиус шара, описанного около куба, равен 3.
Найдите площадь поверхности куба.
Ответ:24
1В.2
В шар, площадь поверхности которого равна 100π,
вписан цилиндр. Найдите высоту цилиндра, если радиус
его основания равен 4.
Ответ: 8
2В.2
В шар вписан конус. Найдите высоту конус, если
радиус шара равен 5, а радиус основания конуса равен 4.
2В.1
Ответ: 6
27.11.16
13



 Математика
Математика






