Похожие презентации:
Динамика идеальной жидкости
1. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
2. Уравнение движения невязкой (идеальной) жидкости- уравнение Эйлера
Уравнение движения невязкой (идеальной) жидкостиуравнение Эйлераu
p
(u )u F
t
ui
p
(u j
)ui Fi
t
x j
xi
Уравнение движения идеальной жидкости в поле потенциальных
сил :
F U
С учетом соотношения:
1
(u )u (u 2 ) [u rot u ]
2
u
u2
p
( U ) [u rot (u)]
t
2
3. Интегралы уравнений движения идеальной жидкости
I. Потенциальное (безвихревое) нестационарное движениеu
u2
p
( U ) [u rot u ]
t
2
u 2
p
( U ) 0
t
2
u
rot u 0
u 2
p
U C (t )
t
2
Интеграл Лагранжа
Iа. Установившееся потенциальное движение
u2
p
U C
2
C постоянно во всем объеме и во
времени – интеграл Эйлера.
4. Уравнение Бернулли.
II. Установившееся вихревое движениеu2
p
( U ) [u rot u]
2
u2
p
d ( U ) 0
2
2
u
p
U Cl
2
Движение в поле силы
тяжести
dr
Умножаем скалярно на
элемент линии тока, dr // u
Сохранение энергии вдоль
линий тока
Сl – константа, постоянная вдоль
линии тока
U gz
u2
p
gz Cl
2
5. Уравнение Бернулли
Работа сил давления:Трубка тока
dA p1S1u1dt p2 S2u2dt
u2dt
z
p2
p
u
u1dt
p1
S2‘
S2
S1
S1 ‘
Изменение энергии жидкости в трубке тока
при ее перемещении на udt (разность
энергий на участках u1dt и u2dt):
u22
dE gz2 S 2u2 dt S 2u2 dt
2
u12
( gz1S1u1dt S1u1dt )
2
z2
z1
Уравнение сохранения массы
S1u1dt S2u2dt
x
dE dA
u22
u12
p2 gz2
p1 gz1
const
2
2
6. Поток энергии течений идеальной жидкости
up
(u )u F
t
u
u2
p
( U ) [u rot (u)]
t
2
u
u
u2
p
u
u ( U ) u [u rot (u )]
t
2
Учитывая, что:
u2
u2
p
p u2
p
u ( U ) div u( U ) ( U )divu
2
2
2
0
1 u 2
u2
div[u ( U p)] 0
2 t
2
u [u rot (u )] 0
7.
По теореме Гауссаu 2
u2
u2
dV div[u (
U p)]dV [ u ( U p / )]d S
t V 2
2
2
V
S
Изменение
энергии в
объеме V в ед.
времени
Вектор плотности потока
энергии
Количество энергии, вытекающей
из объема V через поверхность S –
поток энергии
u2
Пэ u( U p / )
2
Изменение энергии жидкости в объеме V определяется энергией
переносимой жидкостью через поверхность этого объема + работа сил
давления над жидкостью внутри объема V
8.
Стационарное течение : изменение энергии во времени =0.Пусть V – объем жидкости в трубке тока
Поток энергии через поверхность
трубки тока = 0
u2
S [ u ( 2 U p / )]d S 0
Sбок
2
2
П
э d S П э dS П э dS A1 u1 (u1 / 2 U1 p1 / ) A2 u 2 (u 2 / 2 U 2 p2 / ) 0
S
A1
A2
u1 A1 t u2 A2 t
Уравнение неразрывности – сохранение вещества
u 2 / 2 U p / const
Вдоль линии тока
9. Сохранение циркуляции в идеальной жидкости
Циркуляция скорости вдоль жидкого контура lГ ud l
u
r(t)
dl
d
d
du
d r
u
d
l
u
r
r
u
dt
dt
dt
dt
d r
dr
u2
u
u
u u ( )
dt
dt
2
u
d r
(u 2 / 2) 0
dt
d
du
du
ud l
r rot ( ) S rot[ ( p / U )] S 0
dt
dt
dt
S
по формуле
Стокса
Из ур-ния
Эйлера
Г ud l const
Теорема Томсона: циркуляция скорости вдоль произвольного жидкого контура
в идеальной однородной жидкости неизменна во времени
10.
Следствие теоремы Томсонаud l const
u
Если rot
u=0 в какой-то точке линии тока, то
Г=rot(u)dS=const=0 при движении вдоль
Г
этой линии тока (при стационарном течении).
Если rot u=0 при t=0 в любой точке, то движение
остается безвихревым (потенциальным) в любой
момент времени.
u
u2
p
( U ) [u rot (u)]
t
2
rot[u ]
t
rot
rot u
Если (x,y,z, t=0)=0, то (x,y,z, t)=0
11. Потенциальное движение
urot u 0
0
div u div ( ) 0
divu 0
2 2 2
2 2 0
2
x
y
z
Уравнение Лапласа
Граничные условия: при обтекании тела
un
n
0
S
Для движущегося тела: жидкость на
неподвижна, поэтому
При движении тела:
(r) 0
при r
un
n
uтn
S
u т n нормальная
составляющая
скорости точек на
поверхности тела
12.
Решения уравнения Лапласа – гармонические функции, производныелюбого порядка от гармонических функций – также гармонические
функции.
Сумма гармонических функций =∑ m также решение уравнения
Лапласа - Принцип суперпозиции
m 0
( m ) 0
Циркуляция скорости в потенциальном потоке, в котором потенциал –
однозначная функция координат во всем пространстве, равна нулю (время t
рассматривается как параметр).
Г ud l u x dx u y dy
dx
dy d ( B A ) B A 0
x
y
Циркуляция Г в потенциальном потоке по контуру, содержащему внутри области
вихревого течения, Г 0, тогда вводят многозначный потенциал, соответствующие
течения называются циркуляционными потенциальными течениями
Г ud l d ( B A ) B A 0
13. Двумерные течения. Функция тока
Плоское ( двумерное) течение:u=(ux, uy)=u(x,y,t)
u x u y
div u
0
x
y
Функция тока =
div u
В двумерном случае
ux
(x,y,t)
y
uy
x
(
) (
) 0
x y
y
x
Полный дифференциал от
d
(время t рассматривается как
параметр)
Уравнение линий тока
dx dy
ux u y
d вдоль линии тока
d
dx
dy
x
y
u y dx u x dy 0
dx
dy u y dx u x dy 0
x
y
14. Функция тока
yВдоль линии тока =const=C
x
Поток жидкости через площадку dl·1
dQ u n dl 1 dl [u x cos( n, x) u y cos( n, y )]
u x dy u y dx d
Расход жидкости через
поверхность AB= не зависит от
формы поверхности и =разности
функции в точках А и В
B
B
A
A
QAB dQ d B A
15. Функция тока ( осесимметричный случай)
Цилиндрические координаты x, r, θПусть u=u(r,
x
x) (θ)
u x ur ur u
div u
0
x
r
r r
θ
r
Функция тока = (r,
Уравнение линий тока
x)
1
ux
r r
ur dx u x dr 0
d
dx
dr ru r dx ru x dr 0
x
r
1
ur
r x
*r
=С вдоль линий
(поверхностей) тока
осесимметиричного
течения
16. Двумерные потенциальные течения. Комплексный потенциал
uxx
ux
y
x
y
uy
y
uy
x
2 2
2 0
2
x
y
div u=0
rot u i0 j 0 k (
y
x
w i
u y
x
u x
) 0
y
2 2
2 0
2
x
y
Условия Коши-Римана в т.ф.к.п.- условия
аналитичности (регулярности) ф.к.п.
Функции и можно рассматривать
как действительную и мнимую части
функции комп. переменного
w - комплексный потенциал
z=x+iy
17.
Для аналитических функции к.п.dw w
( i ) u x iu y
dz x x
dw w
w
dz x (iy )
Комплексная скорость
Вектор действительной скорости на
комплексной плоскости м.б. представлен как
y
z
u u x iu y
u=ux+iuy
iuy
В полярных координатах r, θ
ux
dw/dz
z x iy r (cos i sin ) rei
-iuy
x
ur
r
1
u
l r
Комплексная и действительная скорости имеют равные модули и
действительные части, а мнимые различаются знаком
18. Простейшие двумерные потенциальные течения
Любая аналитическая функция w(z) может характеризовать некоторыйпотенциальный поток
1. Однородный поток.
w u e i z u (cos i sin ) z
dw
u x iu y u (cos i sin )
dz
Действительная скорость
u u x iu y u (cos i sin )
Уравнение линий тока =u (-xsin +ycos )=Сonst
xtg =y+C
19.
2. Плоский точечный источник (сток).i
w a ln z a ln( re ) a(ln r i )
w a ln z
a ln r
a
a C1
Уравнение линий тока
a
ur
r r
1
u
0
r
Полный поток жидкости,
вытекающей из центра (в угле 2 )
Q= B - A =a(θA+2 -θA)= 2 a
Источник
Сток
a=Q/2 - расход жидкости из
источника
20.
3. Плоский циркуляционный потокb
w ln z
i
b
b
w ln( re i ) b ib ln r
i
b ln r
Уравнение линий тока
y
b ln r b ln C
ur
0
r
=С
r C
1 b
u
r r
Циркуляция по контуру охватывающему центр
(по углу 2 )
x
=С
Г= B - A =b(θA+2 -θA)= 2 b
b=Г/2
r=0 – особая точка потока
21.
4. Плоский дипольM 1
w
2 z
M cos
2 r
M 1 i M 1
w
e
(cos i sin )
2 r
2 r
M sin
2 r
Уравнение линий тока →
М – момент диполя
M sin
M y
M
2 r
2 rr
4 C
y
Уравнение линий тока
x 2 ( y C )2 C 2
М
x
22.
Обтекание кругового цилиндраОбтекание кругового цилиндра : диполь + постоянный поток ?
23.
Обтекание кругового цилиндра невязкойжидкостью
Решение уравнения Лапласа по
принципу суперпозиции
y
x
M 1 Г
w u z
ln z
2 z 2 i
z x iy r (cos i sin ) rei постоянный
поток // x
M
Г
u r
cos
2 r
2
диполь
M
ur
u
cos
2
r
2 r
Граничное условие:
M
Г
u r
ln r
sin
2 r
2
циркуляционный
поток
M
u
0
2
2 r0
ur=0 r=r0
M 2 r02u
24.
Т.о. если момент диполя M=2u r 02
, то получаем обтекание цилиндра r0
r02
ur
u 1 2 cos
r
r
r02
Г
u r cos
r
2
r
u r
r
2
0
Г
sin
ln r
2
r02
1
Г
u
u 1 2 sin
r
2 r
r
При r>r0 скорости конечны, особых точек нет
На поверхности цилиндра при r=r0
ur 0
Г
u 2u sin
2 r0
θ>0 против час. стрелки
25.
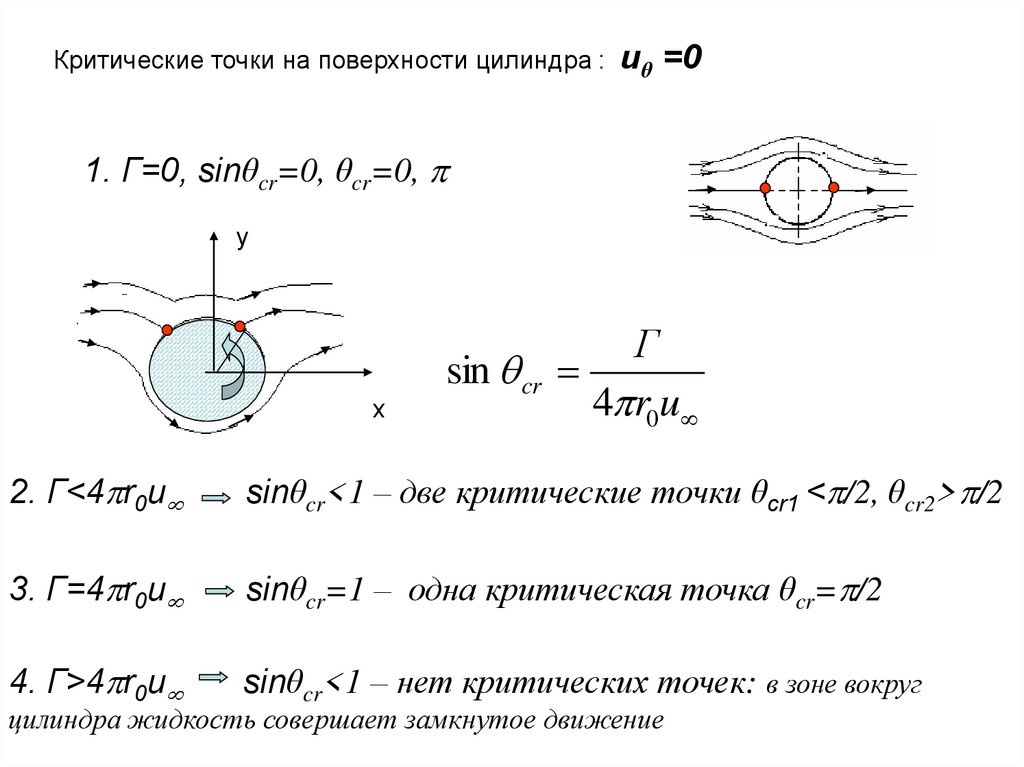
Критические точки на поверхности цилиндра :uθ =0
1. Г=0, sinθcr=0, θcr=0,
y
x
Г
sin cr
4 r0u
2. Г<4 r0u
sinθcr<1 – две критические точки θcr1 < /2, θcr2> /2
3. Г=4 r0u
sinθcr=1 – одна критическая точка θcr= /2
4. Г>4 r0u
sinθcr<1 – нет критических точек: в зоне вокруг
цилиндра жидкость совершает замкнутое движение
26.
Случай Г<4 r0ur02
1
Г
u
u 1 2 sin
r
2 r
r
Скорость на верхней части цилиндра
меньше, чем
скорость на нижней части цилиндра
По теореме Бернулли вдоль линии тока
(здесь pгд=pполн- gz – избыточное, г/д,
давление)
Г
u (r r0 ) 2u sin
2 r 0
Г
u (r r0 ) 2u sin
2 r 0
u / 2 pгд / u / 2 pгд /
2
2
Гидродинамическое давление на нижнюю часть цилиндра < чем на
верхнюю часть : возникает подъемная сила
Объяснение в “https://ru.wikipedia.org/wiki/Подъёмная_сила” и http://masteraero.ru/lp-2.php без циркуляции неверное!, лучше в
http://www.fizportal.ru/qualitative-302
27. Расчет гидродинамических сил при обтекании цилиндра идеальной жидкостью
yR
θ
2
2
0
0
P p ndS p nR d
x
здесь и далее p pгд
I. Расчет горизонтальной компоненты силы г/д давления:
Из Т. Бернулли
2
2
Px p cos 1 Rd (
2
0
0
0
u 2
R 2
2
R cos d
2
u 2
2
u 2
2
( 2u sin
0
p ) R cos d
Г 2
) cos d 0
2 R
Px =0 !!!
28.
Результирующая сил горизонтального давления приобтекании цилиндра в безграничной идеальной
жидкостью потоком с постоянной скоростью =0 .
Парадокс Даламбера: при поступательном
равномерном движении тела в идеальной
жидкости сила сопротивления =0
Нарушается при :
А) наличии вязкости (несимметрия обтекания - след)
Б) непостоянстве скорости потока (присоединенная масса)
В) наличии свободной поверхности (волнообразование)
29.
Влияние вязкости30. II. Расчет вертикальной компоненты силы давления:
22
Py p sin 1 Rd (
2
0
0
0
u 2
R 2
u 2
2
u 2
2
p ) R sin d
Г 2
R sin d
( 2u sin
) sin d
2
2 0
2 R
R 2
Г
Г 2
[4u sin 2
2u sin (
) ] sin d
2 0
2 R
2 R
2
R 2
2
2
0
2
Г
2u sin sin d u Г
2 R
Py u Г
31.
Вертикальная сила при обтекании тел идеальной жидкостью~плотности, скорости набегающего потока и циркуляции вокруг тела.
Направление силы ┴ скорости и повернуто на 90 град относительно u
против направления циркуляции.
Pz u Г lцилиндра
Частный случай теоремы Жуковского о
подъемной силе
“Эффект Магнуса”
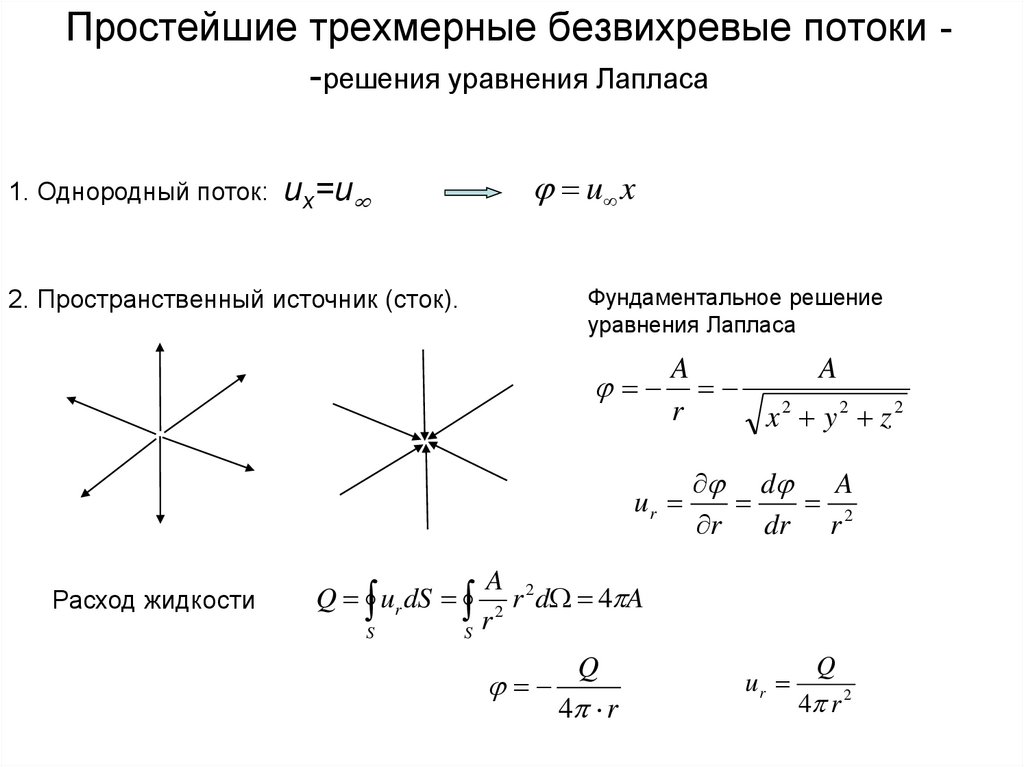
32. Простейшие трехмерные безвихревые потоки - -решения уравнения Лапласа
Простейшие трехмерные безвихревые потоки -решения уравнения Лапласа1. Однородный поток:
u x
ux=u
2. Пространственный источник (сток).
Фундаментальное решение
уравнения Лапласа
A
A
r
x2 y2 z 2
ur
Расход жидкости
Q ur dS
S
S
d A
2
r dr r
A 2
r d 4 A
2
r
Q
4 r
ur
Q
4 r 2
33.
3. Пространственный дипольИсточник
Сток
dn
М
r
r’
lim Qdn 1
Q 1 Q 1
dn 0
lim (
)
( )
r ' r
4 r 4 r '
4
n r
M
1 r
M cos( n, r )
( 2 )
4 r n
4
r2
4. Потенциал простого слоя : источники с интенсивностью q
распределены по поверхности
1
4
S (x1, y1, z1)
q( x1 , y1 , z1 )dS
S
r
r ( x x1 ) 2 ( y y1 ) 2 ( z z1 ) 2
Потенциал простого слоя непрерывен в точках
поверхности, а его нормальная производная ( нормальная
скорость) на поверхности терпит разрыв
q
n 1 n 2
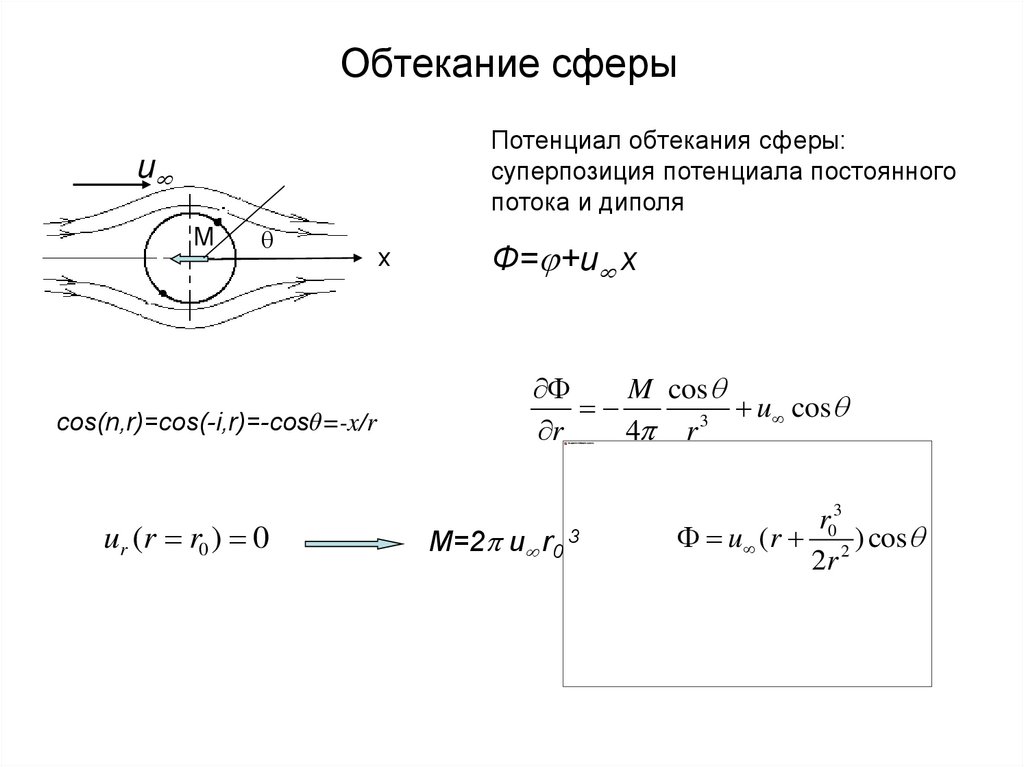
34. Обтекание сферы
Потенциал обтекания сферы:суперпозиция потенциала постоянного
потока и диполя
u
M
θ
cos(n,r)=cos(-i,r)=-cosθ=-x/r
ur (r r0 ) 0
x
Ф= +u x
M cos
u cos
3
r
4 r
M=2 u r0 3
r03
u (r 2 ) cos
2r
35. Формулы Чаплыгина для гидродинамической реакции при обтекании контура
yu
l1
2
gy
2
l
g
u
ux
u
u
2
2
p
pи _ гд
const
u
2
2
pи _ гд
( gy
Const
uy
n
R
x
1. Гидродинамическая реакция
u 2
u 2
n dl
R iRx jRy p n dl 1 Const
n dl
2
2
l
l
l
pст
)
36.
Rxl
u 2
2
cos( n, x) dl
l
u 2
2
Ry
sin dl
Комплексная реакция
l
Rx iR y
u 2
2
cos( n, y ) dl
На линии тока
2
w= +i
dn
dl un dn ul dl udl
n
l
dw
u x iu y u (cos i sin )
dz
i dw
i dw
Rx iR y
dw
dz
2 l dz
2 l dz
2
cos dl
i
u (cos i sin ) u dl
2 l
Рассмотрим безвихревое движение, комплексный потенциал
dw d id d
l
u 2
Формула Чаплыгина для
комплексной г/д реакции
37.
2. Момент гидродинамической реакции МЭлементарная комплексная гидродинамическая реакция
dR y idR x
i dw 2
( ) dz
2 dz
Элементарный момент dM относительно начала координат
dw
dM xdRy ydRx Re i ( x iy )( dRx idR y ) Re iz (dRx idR y ) Re z ( ) 2 dz
2 dz
Гидродинамический момент
dw
M Re z ( ) 2 dz
2
dz
l
Вторая формула
Чаплыгина – для
момента сил
давления на контур
Для расчета R и М требуется знание комплексной скорости. Интегралы можно
брать не только по контуру тела l, но по любому контуру l1 в плоскости z
охватывающему тело, если между l и l1 нет полюсов.
38. Обтекание контура безвихревым потоком
Комплексную скорость м. записать в виде ряда Лорана, znотсутствуют, т.к. u конечна на ∞.
Обтекание потоком с постоянной на ∞ скоростью
Г u x dx u y dy
dw
A A
A0 1 22 ...
dz
z z
dw
A0 u e i
dz z
dw
A A
dx
dy d d id dw
dz A0 1 22 ... dz 2 iA1
x
y
dz
z z
l
d =0
Г 2 iA1
dz 2 i, n 1
z n 0, n 1
теорема о вычетах
Комплексная реакция из формулы Чаплыгина
i
A A
i 2 A A
i
Rx iR y A0 1 22 ... dz 0 1 dz 2 i(2 A0 A1 ) i u e i
2 l
z z
2 l z
2
2
39.
Rx u sinR y u cos
R u
Теорема Жуковского о подъемной силе
Комплексный момент из II формулы Чаплыгина
A12 2 A0 A2
du 2
M Re z ( ) dz Re (
)dz Re i ( ) 2 i 2u e i A2
2
dz
2
z
2
l
l
2 Re i 2u e i A2
Для определения силы и момента достаточно знание коэффициентов Аn,
n=0,1,2.
40. Гидродинамические реакции при неустановившемся движении в жидкости. Присоединенная масса.
Поле скоростей в жидкости, связанное сдвижением тела u(x,y,z,t)
u0(t)
x
Tж
Vж Vт
u 2
u02
dV
2
2
Кинетическая энергия жидкости
u 2
( ) dV
Vж Vт u0
Tж
xu02
2
x
(
Vж Vт
u 2
) dV
u0
Присоединенная масса - фиктивная масса жидкости при ее движении со скоростью тела.
Λ зависит от формы тела и направления движения и не зависит от скорости тела и ускорения.
Изменение кинетической энергии жидкости за dt
=работе силы со стороны тела
ж т
x
R
dTж Rxт ж u0 dt Rxж т u0 dt
du
1 dTж
1 d u02
x x 0
u0 dt
u0 dt 2
dt
Уравнение движения тела
( mт x )
du0
Fдв Rxсопр
dt
mт
du0
du
Fдв Rxсопр Rxж т Fдв Rxсопр x 0
dt
dt
41. Вихревые движения жидкости
1. Уравнение неразрывности для вихря Ω=rot uud l rot u ndS
Ω
L
S
Если контур (неподвижный) стягивается в точку, то
L→0, а поверхность S становится замкнутой
n
S
S u
L L
rot u ndS rot u ndS 0
ud l 0
S
L
По теореме Гаусса
S
rot u ndS div (rot u)dV
S
V
Интегральное и дифференциальное уравнения неразрывности для вихря
div (rot u)dV 0
V
div (rot u ) 0
42.
2. Теоремы Гельмгольца для вихревого движения2.1. Кинематическая теорема Гельмгольца
Уравнение неразрывности для вихря
Ω2
Вихревая линия
nб
Ω1
n1
rot u ndS 0
n2
rot u
S2
Sб
Уравнение неразрывности для вихревой трубки
Sб
rot u ndS (..) (..) (..) 0
S
S1
S1
Вихревая трубка
S2
Sб
1n dS 2 n dS 0
S1
Интенсивность вихревой трубки
I n dS
S
S2
I1 I 2 const
Интенсивность вихревой трубки постоянна по ее длине
0
43.
Следствие кинематической теоремы Гельмгольца: вихревая трубкане может заканчиваться в жидкости
1n dS1 2 n dS2
Если бы трубка заканчивалась в жидкости
, то dS→0, тогда бы Ω→∞.
Ω→∞
Вихревые трубки могут начинаться на поверхности тела, жидкости, границе раздела.
Вихри либо распространяются в ∞, либо заканчиваются на поверхности, либо
существуют как вихревые кольца.
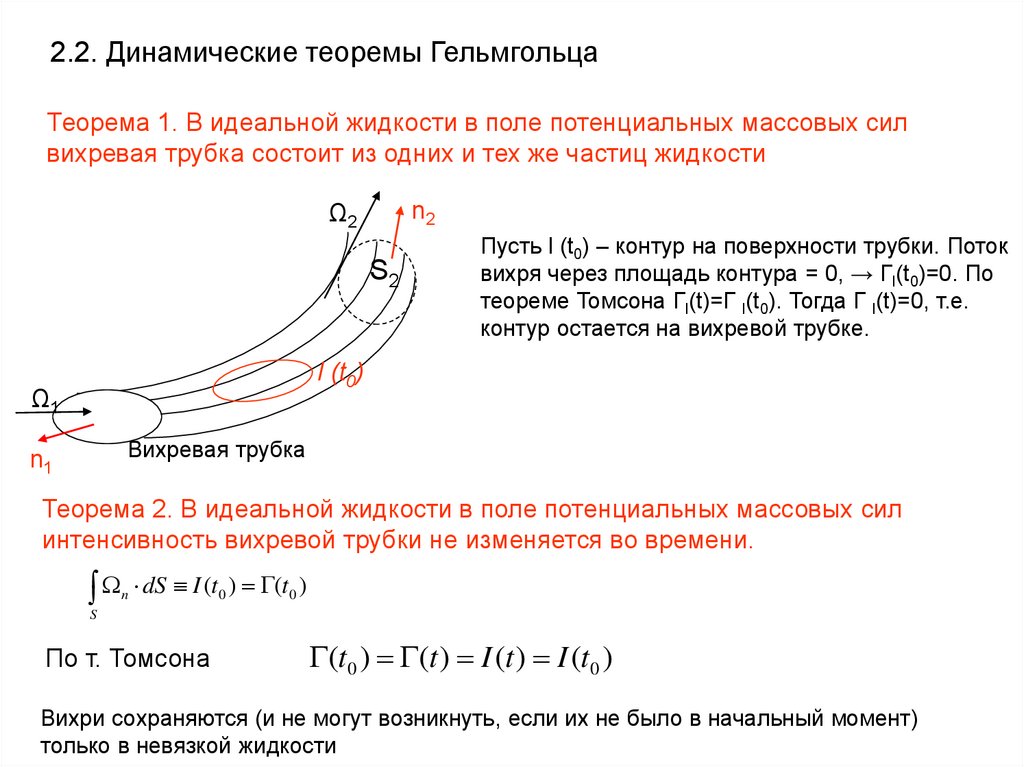
44.
2.2. Динамические теоремы ГельмгольцаТеорема 1. В идеальной жидкости в поле потенциальных массовых сил
вихревая трубка состоит из одних и тех же частиц жидкости
Ω2
n2
S2
Пусть l (t0) – контур на поверхности трубки. Поток
вихря через площадь контура = 0, → Гl(t0)=0. По
теореме Томсона Гl(t)=Г l(t0). Тогда Г l(t)=0, т.е.
контур остается на вихревой трубке.
l (t0)
Ω1
Вихревая трубка
n1
Теорема 2. В идеальной жидкости в поле потенциальных массовых сил
интенсивность вихревой трубки не изменяется во времени.
n
dS I (t0 ) (t0 )
S
По т. Томсона
(t0 ) (t ) I (t ) I (t0 )
Вихри сохраняются (и не могут возникнуть, если их не было в начальный момент)
только в невязкой жидкости
45. Поле скоростей, вызываемых вихревым источником
z(r1) вихревой источник в объеме V
(r1)
u rot A
V
A- векторный потенциал
y
div A 0
Наложим условие
x
rotrot A div A A A
Решение уравнения Пуассона
A
1
4
A
V
Уравнение
Пуассона
( x1 , y1 , z1 )
( x x1 ) ( y y1 ) ( z z1 )
2
2
2
dV
46.
dV dSdlПоле от вихревой трубки
1
Ax
4
dSdl 1
S l x r 4
1
dx1
dS
l r 4
4 S
dSdl 1
cos(
,
x
)
S l
r
4
dy1
Ay
4 l r
dl
dx1 dSdl
S l dl r
dx1
l r
h
l0
r
r0
dS
Az
4
dz1
l r
dy1
dz1
y y1
z1 z
[r 0 l 0 ]x
u x (rot A) x
(
)
( 3 dz1 3 dy1 )
dl
2
4 l z r
y r
4 l r
r
4 l
r
l
Формула Био-Савара
[r 0 l 0 ]
u
dl
2
4 l r
Прямолинейная вихревая трубка
dl ·sin =r·d , h=rsin
2
u
sin
d
(cos 2 cos 1 )
4 h 1
4 h
dl
d
h
r










































 Физика
Физика








