Динамика идеальной жидкости

1.

Динамика идеальной
жидкости
Касабеков М.И.
для студентов специальности В056-5403
«Механика-прикладная математика»
»
Лекции 5, 6
1
03.10.2023

2.

Введение
Идеализация жидкости дает хорошее
соответствие результатов при описании
реальных течений капельных
жидкостей и газов на достаточном
удалении от омываемых твердых
поверхностей и поверхностей раздела с
неподвижной средой.

3.

План лекции
Уравнение движения идеальной
жидкости и его решения
Уравнение Бернулли для несжимаемой
жидкости и примеры его применения
– Истечение жидкости через отверстия
– Определение геометрических
характеристик карбюратора
Лекции 5, 6
3
03.10.2023

4.

Словарь терминов
Идеальной называют воображаемую жидкость,
лишенную вязкости и теплопроводности.
В ней отсутствует внутреннее трение, она
непрерывна и не имеет структуры.

5.

Уравнение движения идеальной
жидкости (уравнение Эйлера)
Уравнение движения идеальной жидкости
получают путем исключения из уравнения
Навье-Стокса слагаемых, в которых в
качестве сомножителя имеется коэффициент
динамической вязкости
dV
2
F grad p divV Div 2
dt
3
0
dV
F grad p
dt

6.

Полная производная вектора скорости по
времени математически эквивалентна сумме
слагаемых, в которые входят удельная
кинетическая энергия жидкой частицы (V2/2)
и вектор угловой скорости (w)
V 2
dV V
2w V
grad
dt
t
2
Подстановка этого выражения в уравнение
Эйлера преобразует последнее в уравнение
движения идеальной жидкости в форме
Громеки-Ламба
V 2
V
1
2w V F grad p
grad
t
2

7.

В гидравлике широко используют понятие потенциала,
который выступает в качестве характеристики
векторного поля
Словарь терминов
Векторное поле a(r) называют
потенциальным, если существует такая
скалярная функция j(r) , называемая
потенциалом векторного поля, градиент
которой в рассматриваемой точке равен
вектору в этой же точке
a r gradj r
Лекции 5, 6
7
03.10.2023

8.

Объемные силы, под действием
которых возможно равновесие
жидкости, имеют потенциал. Например,
сила тяжести имеет потенциал F(r) и
выражается через него
F gradF

9.

В уравнение движения входит плотность
жидкости, зависящая в общем случае от
температуры и давления. Однако в
природе происходит множество
процессов в которых плотность
однозначно определяется только
давлением
p

10.

Словарь терминов
Жидкость, у которой плотность является
функцией только давления, называют
баротропной.
Функцией давления баротропной жидкости
называют интеграл следующего вида
P p
Лекции 5, 6
dp
10
03.10.2023

11.

Поскольку
d
dp
d p
1
dp
dp
то путем следующих формальных
преобразований получаем
dp
gradp
n
gradp grad
dn
d
dp
d
grad
n
dn
d
1
grad
gradp gradp
dp

12.

Величина
1
gradp
представляет собой главный вектор сил
давлений в данной точке, отнесенный к
единице массы, т.е. вектор объемного
действия сил давления.
Следовательно, функция давления Р,
градиент которой равен вектору
объемного действия сил давления,
представляет собой потенциал объемного
действия сил давления.

13.

Заменив в уравнении движения
идеальной жидкости в форме ГромекиЛамба массовые силы и силы давления
на выражения через их потенциалы,
получим векторную форму уравнения
Эйлера-Громеки:
V
V
2w V grad F
t
2
2

14.

Интеграл Эйлера
Интеграл Эйлера является решением
уравнения Эйлера-Громеки в случае
потенциального установившегося
движения.

15.

Словарь терминов
Потенциальным называют движение
жидкости, поле скоростей которой
имеет потенциал j x, y, z
V grad j
Потенциальное течение всегда безвихревое, т.е.
в нем отсутствует вращение жидкости
rotV 0 или w 0
Установившимся называют движение, у
которого скорость не изменяется с
V
течением времени.
0
15
Лекции 5, 6
03.10.2023
t

16.

Для потенциального установившегося
течения уравнение Эйлера-Громеки
примет вид
V2
0
grad F
2
Равенство нулю градиента функции
означает, что
2
V
F
const
2
Это выражение называют интегралом
Эйлера

17.

В случае действия на жидкость только
сил тяжести F g , потенциал
массовых сил определяется следующим
выражением:
F
Fz
g,
z
откуда
F gdz,
или
F gz const

18.

Заменяя в интеграле Эйлера потенциал
массовых сил и функцию давления их
выражениями, получим уравнение Эйлера
2
dp V
gz
const
2
gz
– потенциальная энергия положения частицы
dp
– потенциальная энергия объемного действия
V
2
жидкости единичной массы в поле сил тяжести;
сил давления;
2 – кинетическая энергия частицы жидкости
единичной массы.

19.

С точки зрения механики уравнение
Эйлера представляет собой закон
сохранения энергии для потенциального
установившегося течения жидкости –
сумма всех видов энергии, отнесенных
к единице массы жидкости, во всех
точках потока имеет одно и то же
значение.

20.

Интеграл Бернулли
Интеграл Бернулли представляет собой
решение уравнения Эйлера-Громеки в
случае установившегося не
потенциального движения.

21.

При установившемся не потенциальном
(вихревом) течении справедливы
следующие выражения:
V
0 и w 0
t
т.е. не происходит изменения скорости
жидкости во времени, а ее частицы
имеют возможность участвовать во
вращательном движении. Для таких
потоков уравнение Эйлера-Громеки
примет вид
2
V
2w V grad F
2

22.

В условиях установившегося движения
линии тока и траектории совпадают.
Элемент dL пути, пройденного частицей
жидкости вдоль траектории в
направлении течения, определяют по
формуле
dL Vdt
V
dL

23.

Найдем скалярное произведение
уравнения Эйлера-Громеки и
полученного выражения
V 2
2w V Vdt grad F dL
2
Левая часть данного уравнения равна
нулю, так как является скалярным
произведением двух взаимноперпендикулярных векторов
w V и V

24.

Следствием этого является равенство
нулю первого сомножителя, стоящего в
правой части уравнения, поскольку
элемент пути dL отличен от нуля.
2
V
0
grad F
2
Равенство нулю градиента функции в
условиях установившегося потока
означает, что
2
V
F
const
2
Это выражение называют интегралом
Бернулли.

25.

Из него следует, что в установившемся
не потенциальном потоке сумма всех
видов энергии постоянна лишь вдоль
одной и той же траектории (линии
тока).
Выделенная фраза подчеркивает отличие
интеграла Бернулли от интеграла Эйлера,
справедливого для любых точек
установившегося потенциального потока.

26.

Уравнение Бернулли для
несжимаемой жидкости и
примеры его применения
При течении капельных жидкостей и
газов, когда скорость движения
последних значительно меньше скорости
распространения в них звуковых
колебаний [V<(100-150) м/с],
сжимаемостью среды можно пренебречь
и считать ее плотность постоянной.

27.

В этом случае функция давления становится
равной
Ρ
dp
p
const
Рассматривая в качестве массовых сил только
силы тяжести, обладающие потенциалом
F gz
преобразуем интеграл Бернулли к виду
p
2
V
gz
const
2
который получил название уравнения
Бернулли.

28.

Для двух точек, расположенных на одной
и той же линии тока в разных сечениях
потока идеальной несжимаемой
жидкости, это уравнение записывают в
одной из следующих форм:
p1
2
2
V1
p 2 V2
gz1
gz 2
;
2
2
2
2
p1 V1
p 2 V2
z1
z2
;
g 2 g
g 2 g
2
2
V1
V2
gz1 p1
gz 2 p 2
2
2

29.

При движении реальной жидкости имеет место
неравномерное распределение скорости частиц в
поперечном сечении потока. Для учета этой
неравномерности в уравнение Бернулли вводят
коэффициент кинетической энергии a, который
равен отношению действительной кинетической
энергии весового секундного расхода потока к его
средней кинетической энергии, вычисленной по
средней скорости в данном сечении.
V dS
3
a
S
3
ср
V S
Величину коэффициента a обычно определяют
опытным путем (для установившегося слабо
деформированного потока a 1,1, а для развитого
ламинарного движения a 2).

30.

Вследствие наличия гидравлических
сопротивлений при движении реальной
жидкости, часть энергии потока
расходуется на их преодоление.
Поэтому в последующем (во втором)
сечении энергия потока меньше, чем в
начальном (первом) на величину
p w
hw
g
равную некоторой доли энергии,
необратимо превращенной в тепловую.

31.

Учитывая вышеизложенное, получим для
любых двух рассматриваемых сечений
потока уравнение Бернулли для реальной
несжимаемой жидкости
p1 a V
z1
g
2g
2
1 1ср
p 2 a 2V
z2
g
2g
2
2 ср
hw
Все слагаемые данного уравнения имеют размерность
длины. Их принято называть высотами или напорами:
z
– геометрический (нивелирный) напор;
p g – пьезометрический напор;
V
2
ср
2 g – скоростной напор,
hw
– потеря напора.

32.

Истечение жидкости через
отверстия
В технике большое практическое
значение имеют вопросы истечения
жидкости через отверстия и короткие
патрубки, называемые насадками. В
одних случаях отверстие служит для
пропуска и измерения расхода
жидкости. В других – для создания
компактных и дальнобойных струй.
Отверстия форсунок обеспечивают
распыливание жидкостей.
Лекции 5, 6
32
03.10.2023

33.

В теории истечения различают:
малые отверстия – отверстия, размеры
которых значительно меньше глубины
погружения их центров тяжести под
свободной поверхностью жидкости.
Напоры для всех точек таких отверстий
считают одинаковыми, равными
напорам в центрах тяжести отверстий;
Лекции 5, 6
33
03.10.2023

34.

отверстия в тонких стенках – отверстия
с фасками или заостренными кромками
в стенках, толщины которых не влияют
на условия истечений и формы струй;
отверстия в толстых стенках –
отверстия в стенках, толщины которых
превышают утроенный линейный
размер отверстия. При истечении
жидкости через них струи сначала
сужаются, а затем, расширяясь в
пределах самих отверстий, заполняют
полностью их поперечные сечения.
Лекции 5, 6
34
03.10.2023

35.

отверстия с совершенным и полным сжатием
– отверстия, к которым жидкость движется со
всех сторон по плавно изменяющимся
траекториям. Крайние струйки придают
вытекающей струе коноидальную форму, в
результате чего происходит сжатие ее со всех
сторон и деформация под действием сил
поверхностного натяжения. Отверстие при
этом должно располагаться на расстоянии
большем утроенного его диаметра от стенки,
расположенной перпендикулярно плоскости
отверстия. Наибольшее сжатие струи
наблюдается на расстоянии, приблизительно
равном половине диаметра отверстия;
Лекции 5, 6
35
03.10.2023

36.

Словарь терминов
Струи, которые при истечении не
смешиваются с окружающей средой,
называют свободными.
Струи, которые при истечении
смешиваются с окружающей средой,
называют затопленными.
Лекции 5, 6
36
03.10.2023

37.

Истечение жидкости через
малое отверстие в тонкой стенке
при постоянном напоре
p0
A
hw
A
C
с
O
hс
Sc
H=const
0
pс
O
Sо
l=0,5d
C

38.

Для определения скорости
установившегося истечения жидкости
под постоянным напором через малое
отверстие в тонкой стенке
воспользуемся уравнением Бернулли
для точек «0» и «с», находящихся на
одной траектории
p 0 a 0V
p с a сV
H
hw
g
2g
g
2g
2
0
2
с

39.

Последнее слагаемое в правой части уравнения
представляет собой потерянную часть напора
вследствие трения жидкости о стенки
отверстия и ее деформации. Его значение
определяют по формуле
2
с
V
hw o
2g
Вследствие потери напора при прохождении
жидкости через отверстие напор hc в сечении
струи С-С, измеренный при помощи трубки
Пито, окажется меньше геометрического
напора H. Он равен скоростному напору
жидкости в рассматриваемом сечении
Vс2
hс
2g

40.

Отношение потерянного напора hw к
напору, превращенному в скоростную
энергию hc, представляет собой
коэффициент сопротивления z0,
учитывающий местные потери энергии
в пределах отверстия.

41.

Представим приведенное выше
уравнение Бернулли в следующем виде
p 0 p с a 0V
V
H
H 0 a с о
g
2g
2g
2
0
где H0 – полный напор.
2
с

42.

При постоянном напоре H в резервуаре
скорость V0 на свободной поверхности
жидкости равна нулю. Тогда из
последнего уравнения найдем скорость
в сжатом сечении струи
Vс
p0 pc
2 g H
g
aс о
где j 1
скорости.
p0 pc
или Vс j 2 g H
g
aс о
– коэффициент

43.

При истечении идеальной жидкости,
для которой о 0
и aс 1 ,
скорость движения в струе
максимальная, равная
p0 pc
Vи 2 g H
g

44.

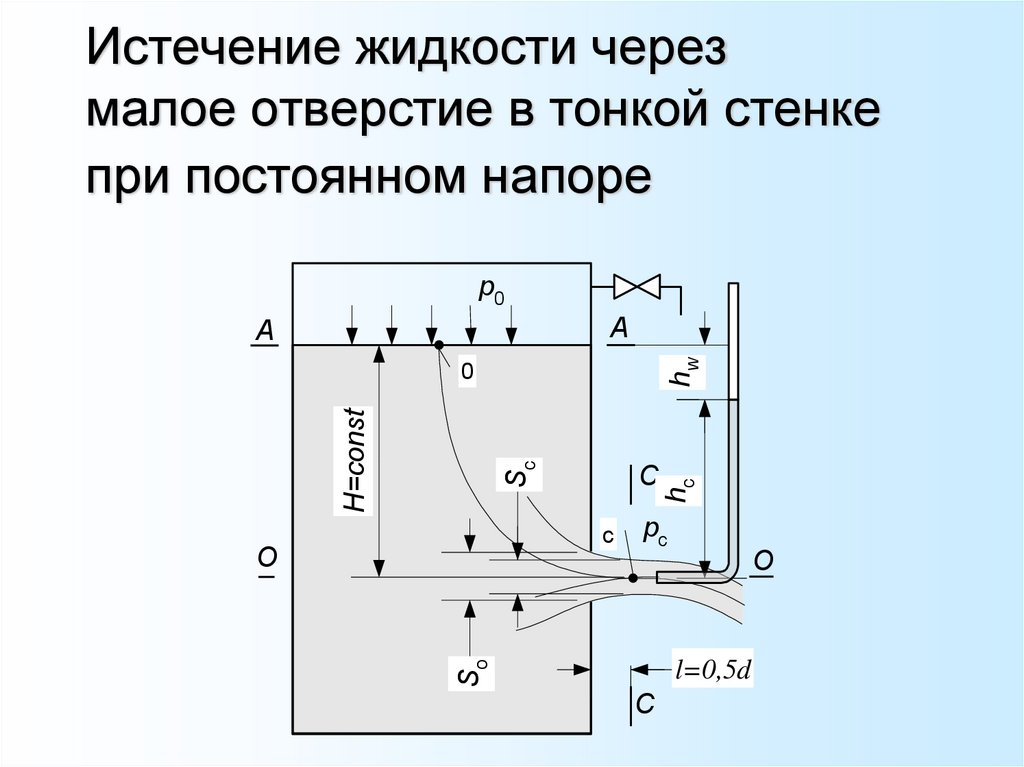
Словарь терминов
Отношение скоростей истечения
реальной и идеальной жидкостей
называют коэффициентом скорости
Vc
j
1
Vи
Он учитывает местные гидравлические
сопротивления в отверстии и
неравномерность распределения
скоростей в сжатом сечении.
Лекции 5, 6
44
03.10.2023

45.

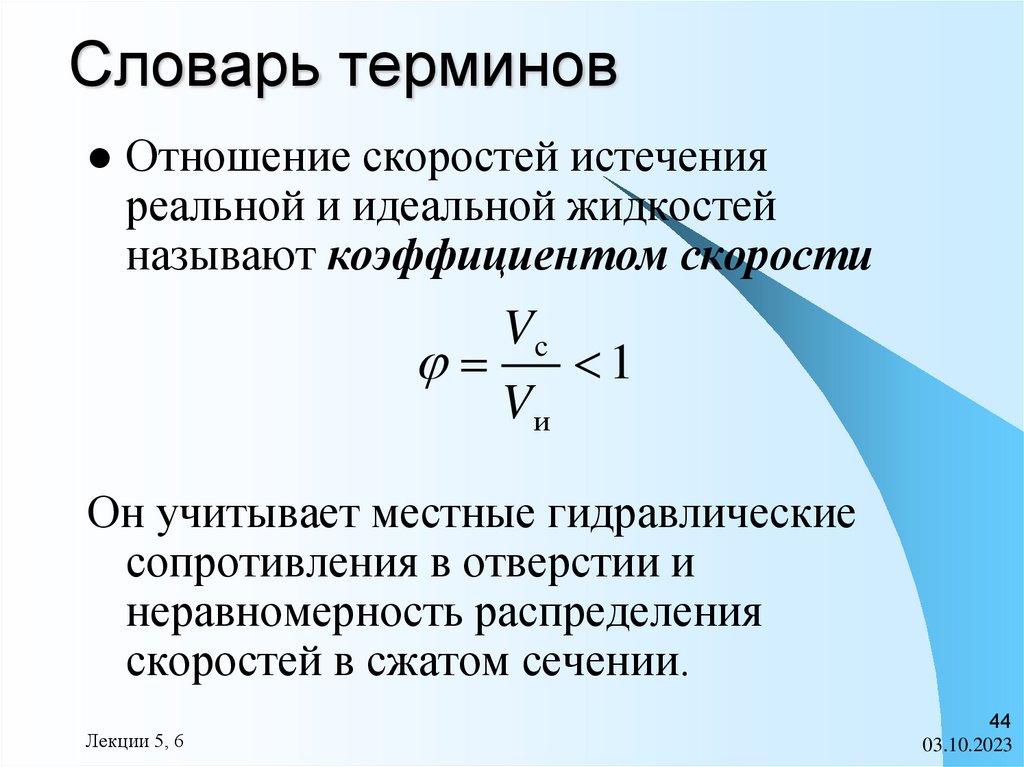
Словарь терминов
Сжатие струи, вытекающей из отверстия,
учитывают при помощи коэффициента
сжатия
Sс
Sо
который равен отношению площади струи Sс
в узкой ее части к площади отверстия Sо
Лекции 5, 6
45
03.10.2023

46.

Объемный расход жидкости, протекающей
через узкое сечение струи
p0 pc
p0 pc
S о 2 g H
Q S сVс S о j 2 g H
g
g
Теоретический расход определяют по
формуле
Q т S оV и S о
p0 pc
2 g H
g

47.

Словарь терминов
Отношение действительного расхода
жидкости к теоретическому называют
коэффициентом расхода
Q
j 1
Qт
Лекции 5, 6
47
03.10.2023

48.

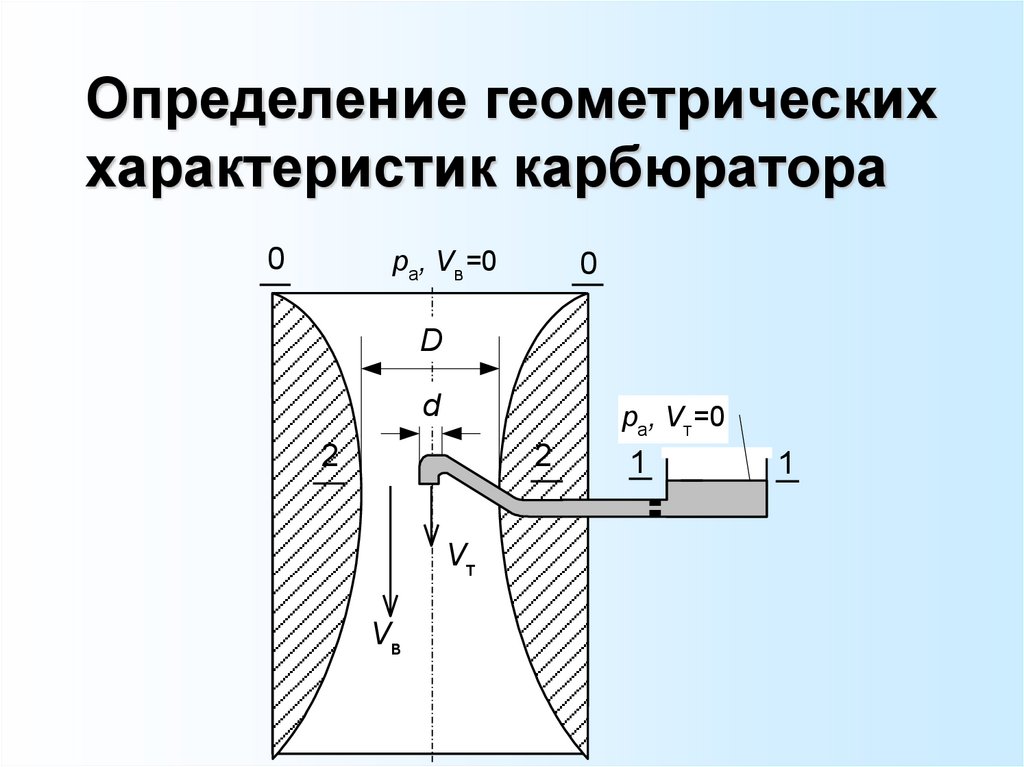
Определение геометрических
характеристик карбюратора
0
pа, Vв=0
0
D
d
pа, Vт=0
2
2
Vт
Vв
1
1

49.

Карбюратор поршневых двигателей внутреннего
сгорания предназначен для создания топливновоздушной смеси определенного состава. Поток воздуха,
засасываемого в рабочие цилиндры, проходит через
сужающийся воздушный канал карбюратора, в узком
месте которого расположено отверстие для подачи
топлива, соединенное с поплавковой камерой.
Повышение скорости потока воздуха за счет уменьшения
площади проходного сечения карбюратора вызывает, в
соответствии с уравнением Бернулли, снижение
давления. Понижение давления в месте окончания
топливного канала приводит к истечению топлива в
воздушный поток.

50.

Задача расчета карбюратора сводится к
определению таких его геометрических
параметров, которые обеспечат
необходимое соотношение топлива и
воздуха в смеси.

51.

Известны:
соотношение между массовыми
расходами топлива и воздуха G т G в
соответствующие условию полного
сгорания;
плотности топлива т и воздуха в ;
диаметр D узкого сечения воздушного
канала карбюратора;
суммарный коэффициент сопротивления
воздушного канала в и топливного т
с расположенным в нем жиклером.

52.

Определить:
диаметр отверстия топливного канала d,
обеспечивающий заданное соотношение
расходов компонентов топливновоздушной смеси.

53.

Запишем уравнение Бернулли для потока
воздуха между сечениями 0-0 и 2-2
(параметры в сечении 2-2 обозначим
индексом 2). Из-за невысокой плотности
воздуха геометрическим напором,
обусловленным разностью уровней
рассматриваемых сечений, пренебрегаем.
pa
в g
2
2в
2
2в
2
2в
p2 V
p2 V
V
hwв
в
в g 2 g
в g 2 g
2g
pa p2 1 в
V
2
в 2в
2
.

54.

Уравнение Бернулли для потока
топлива между сечениями 1-1 и 2-2 при
z1=z2 имеет вид:
pa
т g
2
2т
2
2т
2
2т
p2 V
p2 V
V
hwт
т
т g 2 g
т g 2 g
2g
pa p2 1 т
V
2
т 2т
2
.

55.

Из представленных уравнений следует,
что
1 т
тV
2
2т
2
1 в
вV
2
2в
2
V2 т
1 в в
1 т т
V2в
2
Выразим скорости воздуха и топлива
через их массовые расходы, плотности
и площади проходных сечений каналов,
по которым они движутся.
Gв в
V2 в
2
D 4
Gт т
и V2 т
2
d 4

56.

Подстановка данных выражений в
предыдущую зависимость приводит к
следующему итоговому уравнению
Gт
d D
Gв
1 т в
1 в т
12

57.

Выводы

58.

Источники дополнительных
сведений