Похожие презентации:
Потенциальные течения
1. Потенциальные течения
Для наглядности будем рассматривать двумерный случай движения частиц жидкости.В общем случае элементарная частица жидкости перемещается с поступательной
скоростью, деформируется и вращается вокруг оси, проходящей через частицу.
В плоском случае, вращение может происходить только вокруг оси, перпендикулярной
плоскости течения. Угловая скорость вращения частицы:
1 v u
Обозначим величину ω – местной завихренностью.
2 x y
Безвихревым называется движение жидкости при ω = 0 во всей рассматриваемой
области. В противном случае течение называется вихревым. v u
0
Условием безвихревого течения является: x y
Введем понятие циркуляция скорости Г по замкнутому контуру l :
Где l - проекция скорости на касательную к контуру,
Г l dl
dl – элемент дуги контура.
l
2.
Интеграл по замкнутому криволинейному контуру можно записать вдекартовых координатах и применить формулу Стокса:
Введя местную завихренность получим теорему Стокса: Г 2 ds
S
где ds – элемент площади внутри контура.
Следовательно, если течение безвихревое, то циркуляция скорости по
любому замкнутому контуру равна нулю: Г = 0.
Если циркуляция скорости по данному контуру равна нулю,
то нельзя утверждать, что течение безвихревое. Равна нулю
лишь суммарная завихренность внутри контура.
3. Уравнение Эйлера
Для плоского установившегосядвижения идеальной жидкости:
Введя обозначение
модуля скорости: ω2 = u2 + v2
преобразуем уравнение
в вид Громека – Лэмба:
Для безвихревого движения
уравнения преобразуются в одно
уравнение в полных дифференциалах:
dp
d
0
4. Уравнение Бернулли
Проинтегрировав уравнение при ρ = const,получим уравнение для несжимаемой жидкости:
2 p p0
const
2
Бернулли получил это уравнение в 1738г.,
2 p
gh const
причем с учетом силы тяжести жидкости:
2
где h – высота столба жидкости.
Для изэнтропического течения сжимаемой жидкости в пространственном
течении уравнение Бернулли принимает вид:
2
k p0 p
2 k 1 0 p
0
k 1
k
k p0
const
k 1 0
5. Рассмотрим плоское установившееся безвихревое движение
Для безвихревого движения можно ввести потенциал скорости u xявляющийся функцией φ(x, y), удовлетворяющей условиям:
v
Так как потенциал скорости можно ввести только для
y
безвихревого движения, то такие течения называют потенциальными.
Для выполнения уравнения сохранения массы
2
2
потенциал скорости для несжимаемой жидкости
2 0
2
x y
должен удовлетворять уравнению Лапласа:
Удобно ввести еще функцию тока: ψ(x, y), удовлетворяющую условиям:
, также удовлетворяющую
2
2
уравнению
Лапласа:
u
2 0
v
2
y
x y
x
6.
Линия в жидкости, касательная к которой в любой ее точкепараллельна направлению скорости, называется линией тока.
На линиях тока функция тока принимает
постоянное значение, т.е. уравнение
семейства линий тока: ψ = const.
Производная потенциала скорости
на любое направление : x y
l
x l
y l
Выражение равно
wl
сумме проекций скоростей u и v на направление l:
l
wn 0
Проекция φ на нормаль к линии тока:
n
7.
Рассмотрим сетку, образованную семействомлиний тока ψ = const и линий
равного потенциала φ = const.
Скорости потока касательны к линиям тока
и нормальны к линиям равного потенциала,
следовательно, сетка ортогональна.
Т.к. жидкость не может пересекать линий тока,
то между двумя любыми линиями тока
расход жидкости в любом сечении одинаков.
Расход жидкости через произвольную кривую между точками a и b:
Q w n dl u dy v dx d b a
l
l
l
8.
Жидкость не может пересекать границу твердого тела, а значитпроекция скорости на нормаль к поверхности n 0 , т.е. скорость
должна быть касательная к поверхности тела.
0, const.
На обтекаемой поверхности получаем условия:
n
Они совпадают с определением линии тока, а значит любую линию тока
можно считать твердой поверхностью, и наоборот.
Из основных формул также следует соотношение Коши – Римана:
,
x y
.
y
x
На этом основано применение теории функций комплексного переменного
к расчету плоских потенциальных потоков несжимаемой жидкости:
i F(z), z x iy.
Функция F(z) – комплексный потенциал потока, z – комплексная переменная.
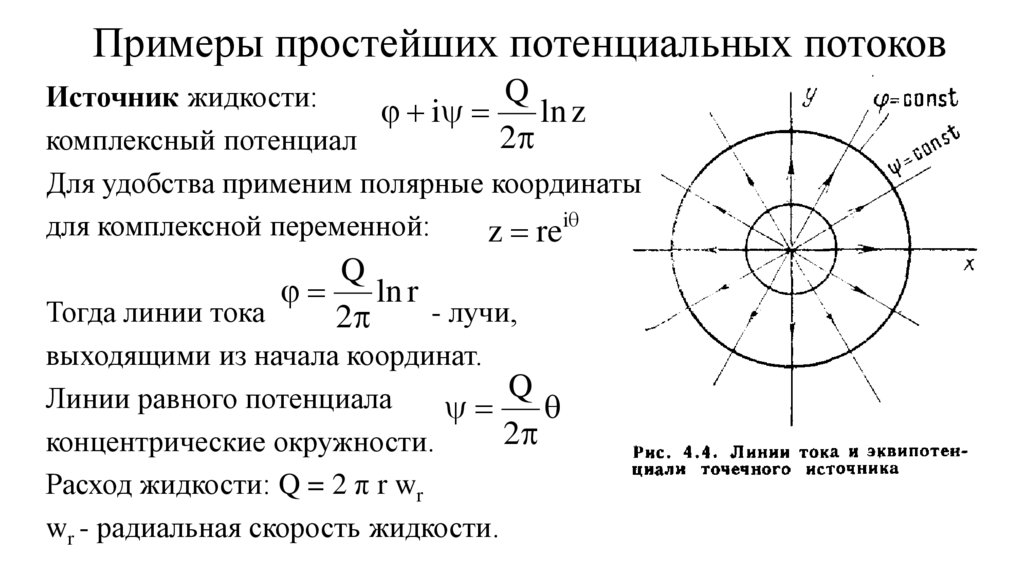
9. Примеры простейших потенциальных потоков
QИсточник жидкости:
i
ln z
2
комплексный потенциал
Для удобства применим полярные координаты
для комплексной переменной:
z rei
Q
ln r
Тогда линии тока
- лучи,
2
выходящими из начала координат.
Q
Линии равного потенциала
2
концентрические окружности.
Расход жидкости: Q = 2 π r wr
wr - радиальная скорость жидкости.
10.
Комплексный потенциал вихря i Г ln z2 i
Г
– окружности,
Линии тока
2
Г
ln r - лучи.
Линии равного потенциала
2
Г 1
Окружная скорость жидкости w
2 r
Величина Г – циркуляция скорости,
характеризует интенсивность вихря,
а знак Г – направление вращения
(положительный – против часовой стрелки)
11.
qКомплексный потенциал диполя i
z
, где q – момент диполя.
Для удобства используем декартову СК:
x
y
2
, 2
.
2
2
x y
x y
Приняв ψ = const, получим семейство
окружностей в центрами на оси ординат.
Линии равного потенциала – семейство
окружностей в центрами на оси абсцисс.
Диполь можно получить в результате слияния источника и стока:
Q
Q
, в пределе h→0 получим диполь, где q=Qh
F(z)
2
ln(z h )
2
ln z
12.
ro2Г
z
Потенциал обтекания окружности: F(z) u (z )
ln
z
2
i
r
o
u z
Состоит из: плоскопараллельного потока
2
z
диполя q = ro ,
вихря Г
ln
В полярной СК функции запишутся
2 i ro
ro2
Г
u (r ) cos
r
2
ro2
Г
r
u (r ) sin ln
r
2 ro
При Г = 0 проекции скорости потока получим:
wr
u (1
r
r
2
ro
Г
w
u (1 2 ) sin
r
2 r
r
2
ro
) cos
2
13. Обтекание плоским потоком произвольного тела
Выделим на контрольной поверхности Sэлементарную площадку ds*l и проведем к ней
внешнюю нормаль п, которая образует с осями
координат углы α и β.
Если проекцию скорости частиц, протекающих
через площадку ds·l, на нормаль п
обозначить через Vn, то очевидно, что масса
жидкости, протекающей в единицу времени
сквозь эту площадку, будет равна Vnds·l.
Количество движения рассматриваемой массы
жидкости, переносимое в единицу времени
сквозь всю контрольную поверхность,
VVn ds
выразится интегралом:
S
14.
Когда скорость невозмущенного потока направлена по оси ОХ и равна V , потенциалскорости можно записать в виде = V x+ '(x, у),
где φ'(x, у) - потенциал добавочных возмущенных скоростей, удовлетворяющих
уравнению Лапласа.
Для проекций скорости Vx, Vy получим соотношения:
Функции φ'(X, у) па бесконечности удовлетворяют
0
x
Vx
V
x
x
Vy
y y
0
y
Выражение
Vn (V
) cos
sin
для скорости Vn принимает вид:
x
y
Полагая, что контур S настолько велик, что в силу граничных условий величинами
условиям:
(д '/дх)г и (д '/ду)2 можно пренебречь, определим произведения VnVХ и VnVv
15.
Для определения силы лобового сопротивления тела X и подъемной силыУ необходимо знать давление и скорость в каждой точке контрольной
поверхности. Подставив в интегралы значение давления, определенное по
формуле Бернулли, получим:
V2
X V Vn ds
cos ds
2 S
Интеграл V ds
S
n
2
V
S
Y
sin ds V Vs ds
представляет собой расход
2 S
S
жидкости сквозь замкнутый контур, для твердого тела он равен нулю.
Из геометрии cos ds 0, получили Х= 0 – парадокс Даламбера–Эйлера.
Проекция скорости на контур: V d V sin cos
s
ds
x
Г Vsds - циркуляция скорости по контуру S.
S
y
Y V Г
16. Теорема Жуковского (1905г.)
Y V ГЕсли поток, имеющий в бесконечности скорость V , обтекает контур, и циркуляция скорости по этому контуру равна Г, то равнодействующую сил давления
жидкости на контур получим, если умножим вектор, представляющий скорость
потока в бесконечности, на циркуляцию скорости и на плотность жидкости.
Если знаки V и Г различны, то сила будет положительна и направлена вверх, при
одинаковых знаках V и Г подъемная сила направлена вниз.
Циркуляция Г может создаваться не реальным, а фиктивным вихрем, Жуковский
назвал его «присоединенным». Циркуляцию можно увеличить различными
способами, например, увеличением кривизны крыла, воздействием на пограничный слой, приведением в движение части поверхности крыла и т.д.
17.
Следует отметить, что вопрос об истиннойвеличине циркуляции скорости, входящей в
формулу Жуковского, является в общем случае
неопределенным. Строго говоря, с точки зрения
теории идеальной жидкости эта величина может
быть произвольной, так что решение задачи об
обтекании профиля получается неоднозначным.
Поэтому любому произвольно выбранному
значению Г соответствует некоторое конкретное
решение.
Постулат Жуковского — Чаплыгина:
При обтекании профиля с острой задней кромкой
физически реализуется такое (единственное)
значение циркуляции, при котором задняя
критическая точка совпадает с задней кромкой.
















 Физика
Физика








