Похожие презентации:
Лекция 4. Преобразование объектов
1.
Лекция 4Преобразование объектов
Нижельский С.С.,
ст. преп. каф. СИУ
Новокузнецк, 2008
2.
Преобразование объектовПусть любая точка, принадлежащая определенному объекту, имеет
координаты (k1, k2, …, kn) в n-мерной системе координат
Тогда преобразование объекта можно определить как изменение положения
точек объекта. Новое положение точки пространства соответствует новым
значениям координат (m1, m2, …, mn)
Соотношение между старыми и новыми координатами для всех точек
объекта
(m1, m2, …, mn) = F(k1, k2, …, kn)
и будет определять преобразование объекта, где F – функция
преобразования
3.
Аффинные преобразования объектов на плоскостиАффинные преобразования объектов на плоскости описывается формулой:
X Ax By C ,
Y Dx Ey F ,
где A, B, …, F – константы; x, y – координаты до преобразования; X, Y –
новые координаты точек объектов.
Рассмотрим частные случаи аффинного преобразования
4.
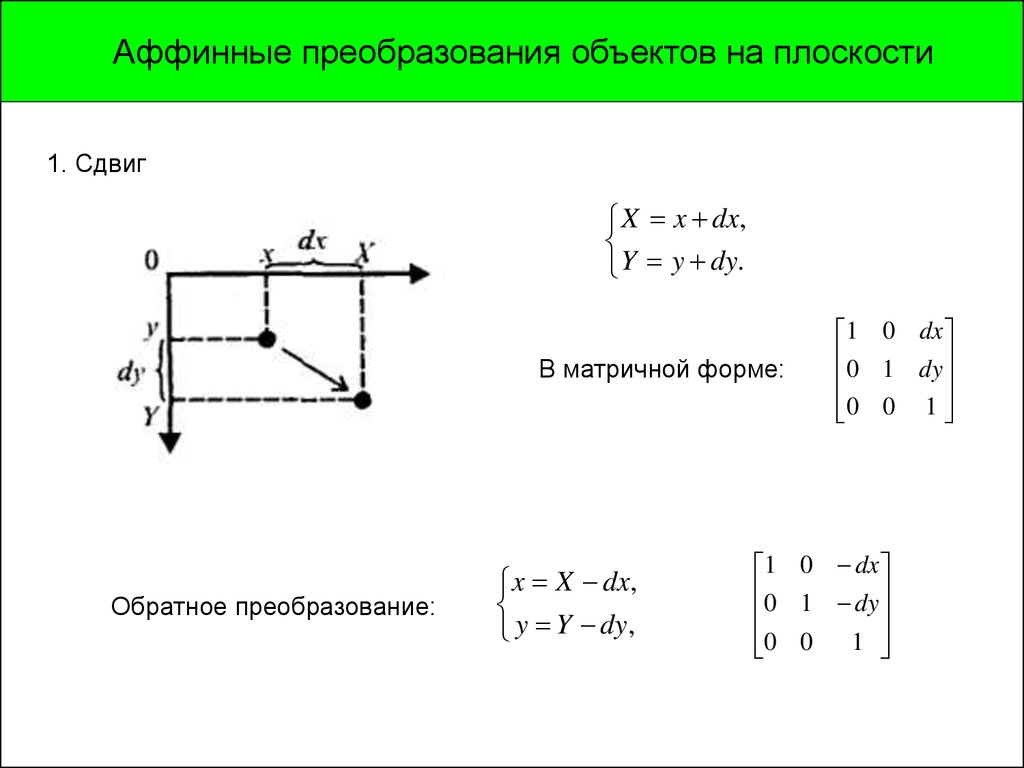
Аффинные преобразования объектов на плоскости1. Сдвиг
X x dx,
Y y dy.
В матричной форме:
Обратное преобразование:
x X dx,
y Y dy,
1 0 dx
0 1 dy
0 0 1
1 0 dx
0 1 dy
0 0
1
5.
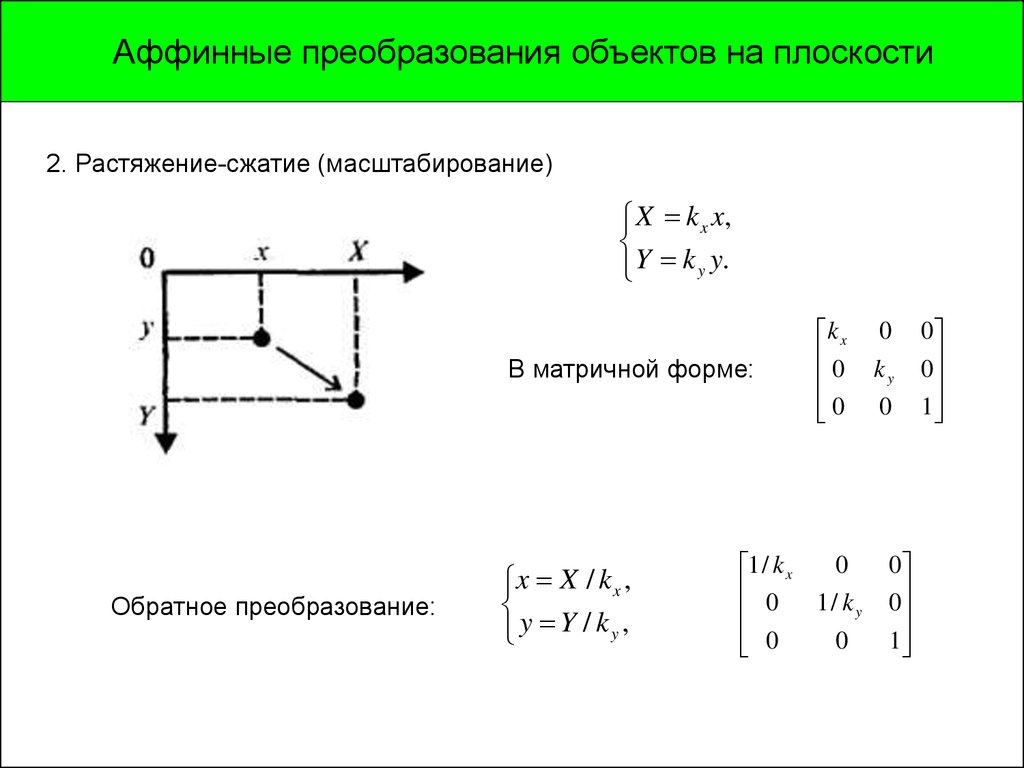
Аффинные преобразования объектов на плоскости2. Растяжение-сжатие (масштабирование)
X k x x,
Y k y y.
В матричной форме:
Обратное преобразование:
x X / k x ,
y Y / ky ,
k x
0
0
0
1 / k x
0 1/ k
y
0
0
0
ky
0
0
0
1
0
0
1
6.
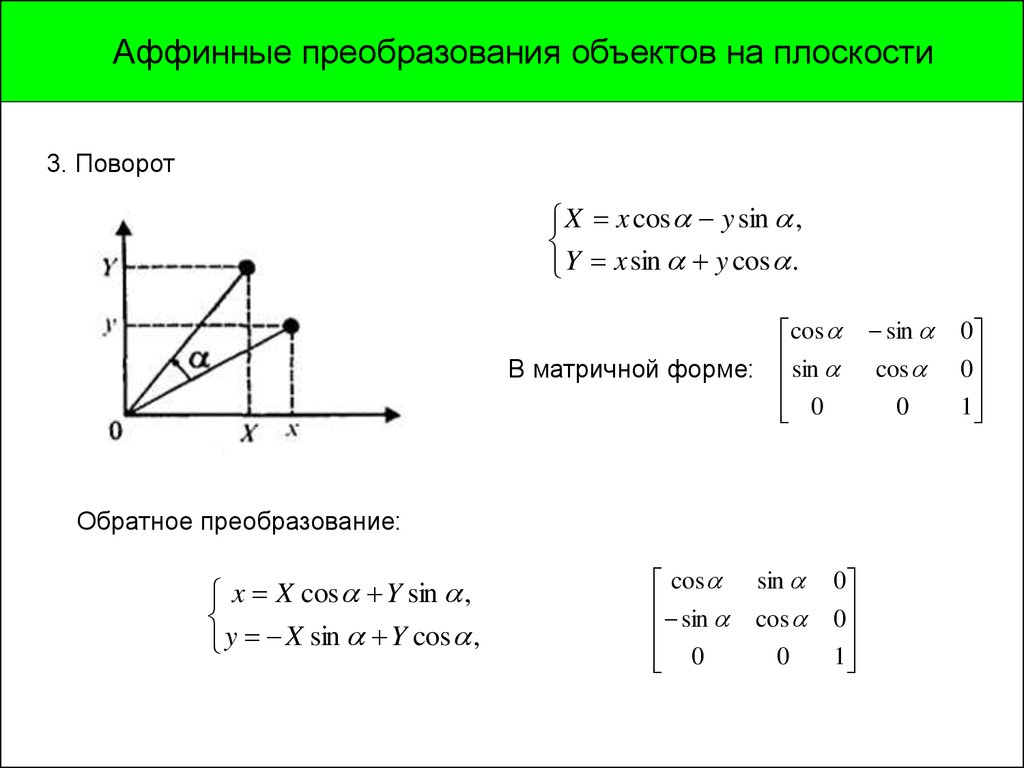
Аффинные преобразования объектов на плоскости3. Поворот
X x cos y sin ,
Y x sin y cos .
В матричной форме:
cos
sin
0
Обратное преобразование:
x X cos Y sin ,
y X sin Y cos ,
cos
sin
0
sin
cos
0
0
0
1
sin
cos
0
0
0
1
7.
Трехмерные аффинные преобразования объектовВ общем виде записываются
X Ax By Cz D,
Y Ex Fy Gz H ,
Z Kx Ly Mz N ,
где A, B, …, N – константы
В матричном виде
X A
Y E
Z K
1 0
B
F
L
C
G
M
0
0
D x
H y
N z
1 1
.
8.
Трехмерные аффинные преобразования объектов1. Сдвиг объектов на dx, dy, dz:
2. Растяжение/сжатие на kx, ky, kz:
.
9.
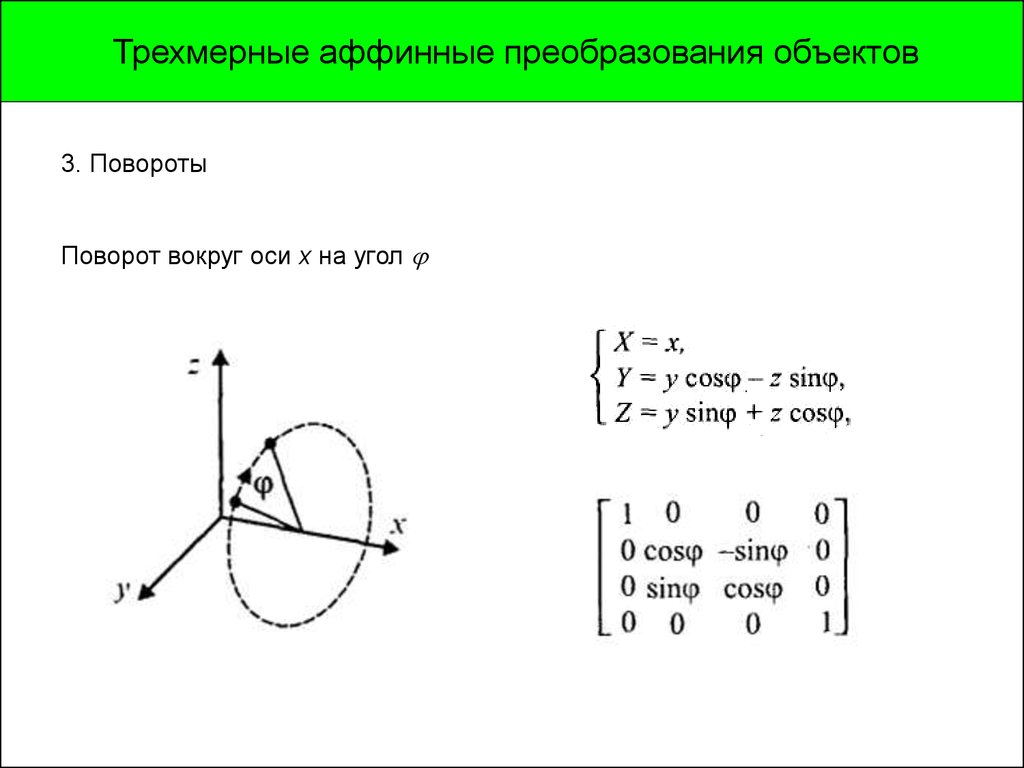
Трехмерные аффинные преобразования объектов3. Повороты
Поворот вокруг оси x на угол
.
10.
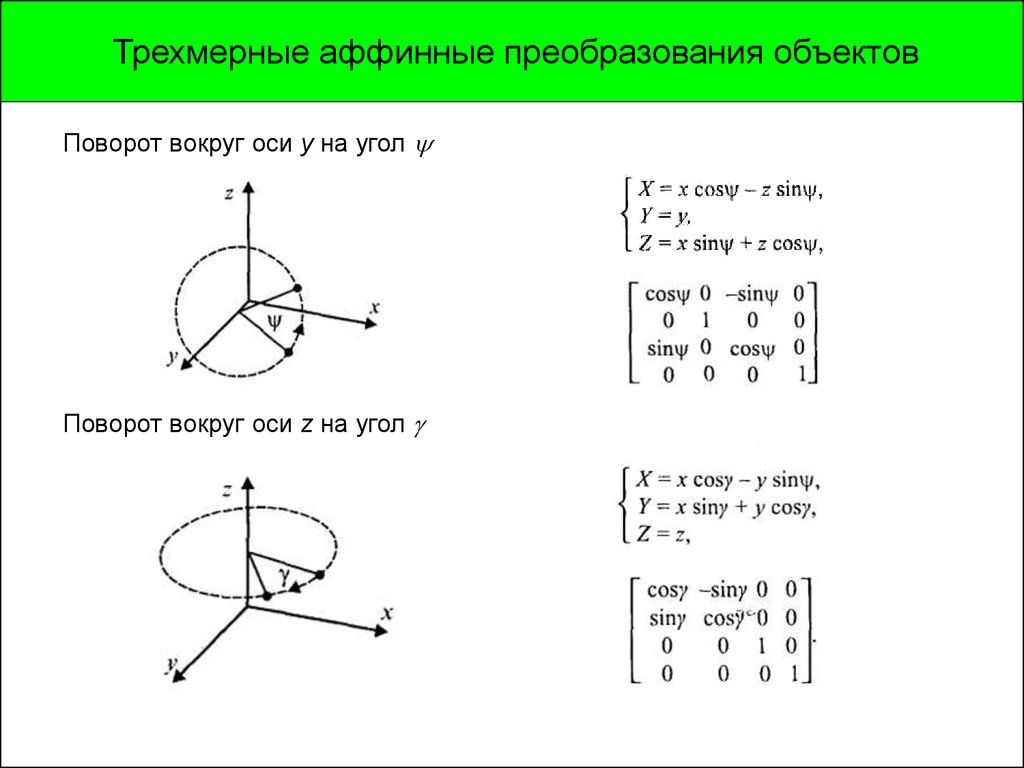
Трехмерные аффинные преобразования объектовПоворот вокруг оси y на угол
Поворот вокруг оси z на угол
.
11.
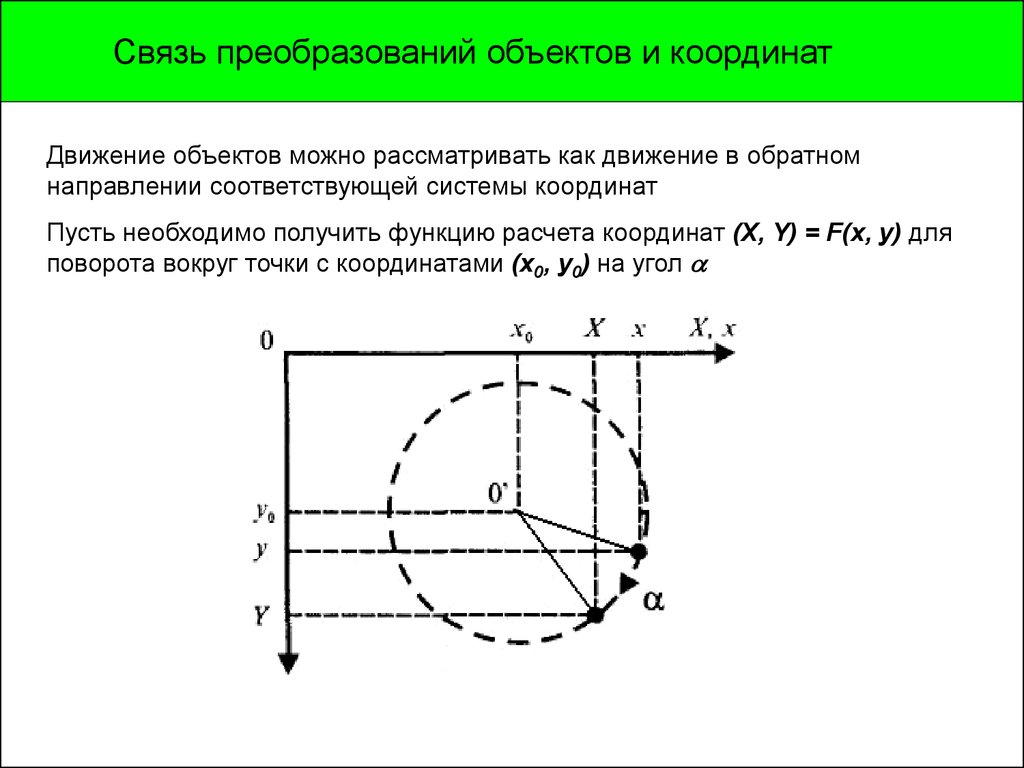
Связь преобразований объектов и координатДвижение объектов можно рассматривать как движение в обратном
направлении соответствующей системы координат
Пусть необходимо получить функцию расчета координат (X, Y) = F(x, y) для
поворота вокруг точки с координатами (x0, y0) на угол
.
12.
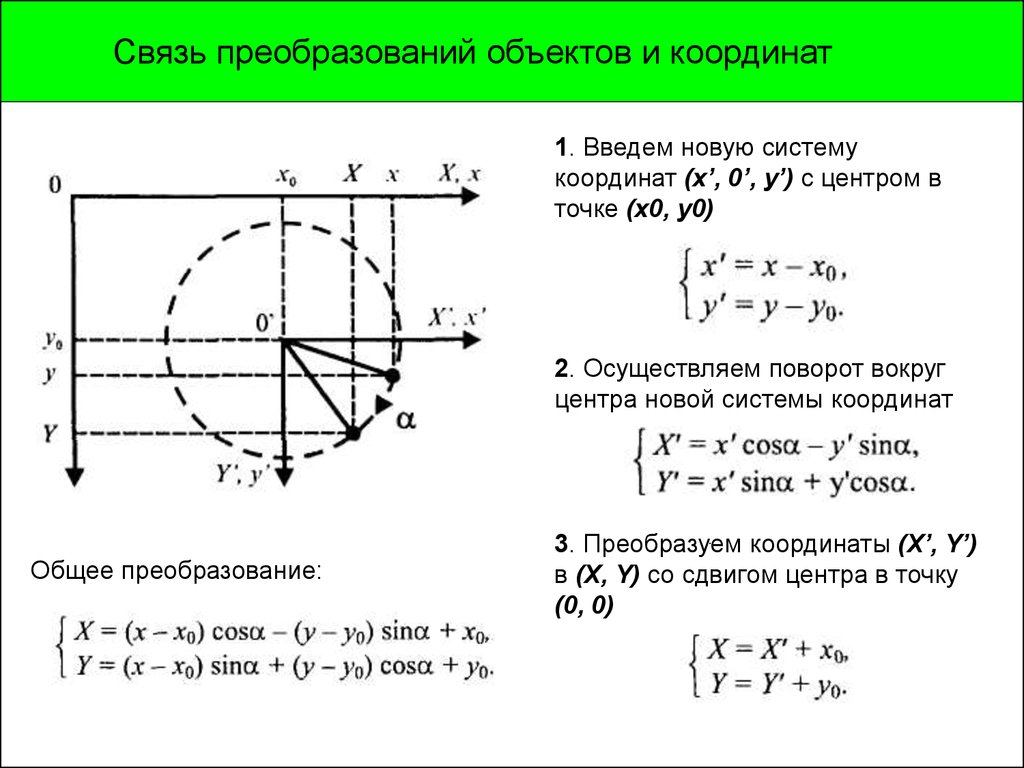
Связь преобразований объектов и координат1. Введем новую систему
координат (х’, 0’, y’) с центром в
точке (x0, y0)
2. Осуществляем поворот вокруг
центра новой системы координат
Общее преобразование:
.
3. Преобразуем
координаты (X’, Y’)
в (X, Y) со сдвигом центра в точку
(0, 0)
13.
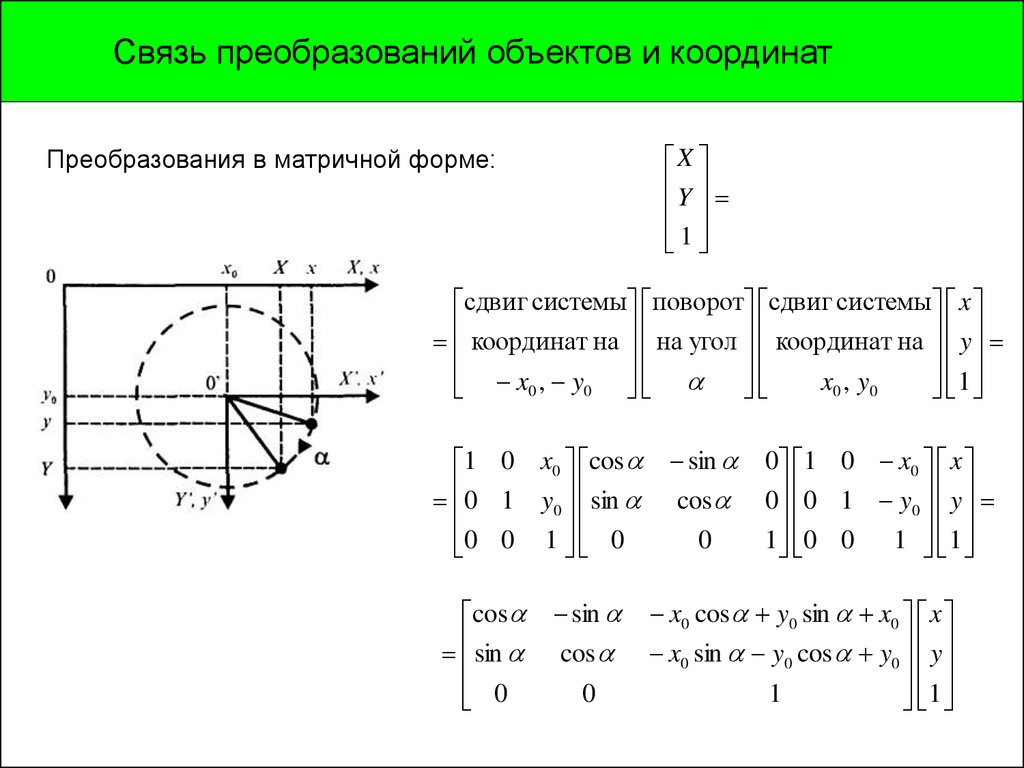
Связь преобразований объектов и координатX
Y
1
Преобразования в матричной форме:
сдвиг системы поворот сдвиг системы x
координат на на угол координат на y
x0 , y0
1
x0 , y0
1 0 x0 cos
0 1 y0 sin
0 0 1 0
cos
sin
0
sin
cos
0
sin
cos
0.
0 1 0 x0 x
0 0 1 y0 y
1 0 0 1 1
x0 cos y0 sin x0 x
x0 sin y0 cos y0 y
1
1





 Информатика
Информатика