Компьютерная графика. Лекция 4. Проекции

1.

КОМПЬЮТЕРНАЯ
ГРАФИКА
Лекция 4
«Проекции»
Лектор, зав. кафедрой, к.т.н.
Степанченко Илья Викторович
Камышин 2009
Кафедра
автоматизированных
систем обработки
информации и
управления

2.

2.7. ПОСТРОЕНИЕ ПРОЕКЦИЙ
Сцена (scene) – двухмерное изображение
трехмерного объекта.
Картинная плоскость (projection plane) –
плоскость, на которой изображается сцена.
Проецирование (projection) (проектирование) –
отображение объекта на картинной плоскости.
картинная
плоскость
Так получают параллельные
проекции
картинная
плоскость
Так получают центральные
проекции

3.

2.7. ПОСТРОЕНИЕ ПРОЕКЦИЙ
a’
картинная
плоскость
b’
c’
а
b
c
a’
картинная
плоскость
b’
c’
а
b
c

4.

2.7.1. КЛАССИФИКАЦИЯ
ПРОЕКЦИЙ
Центральные
проекции
Одноточечная
проекция
Двухточечная
проекция
Трехточечная
проекция

5.

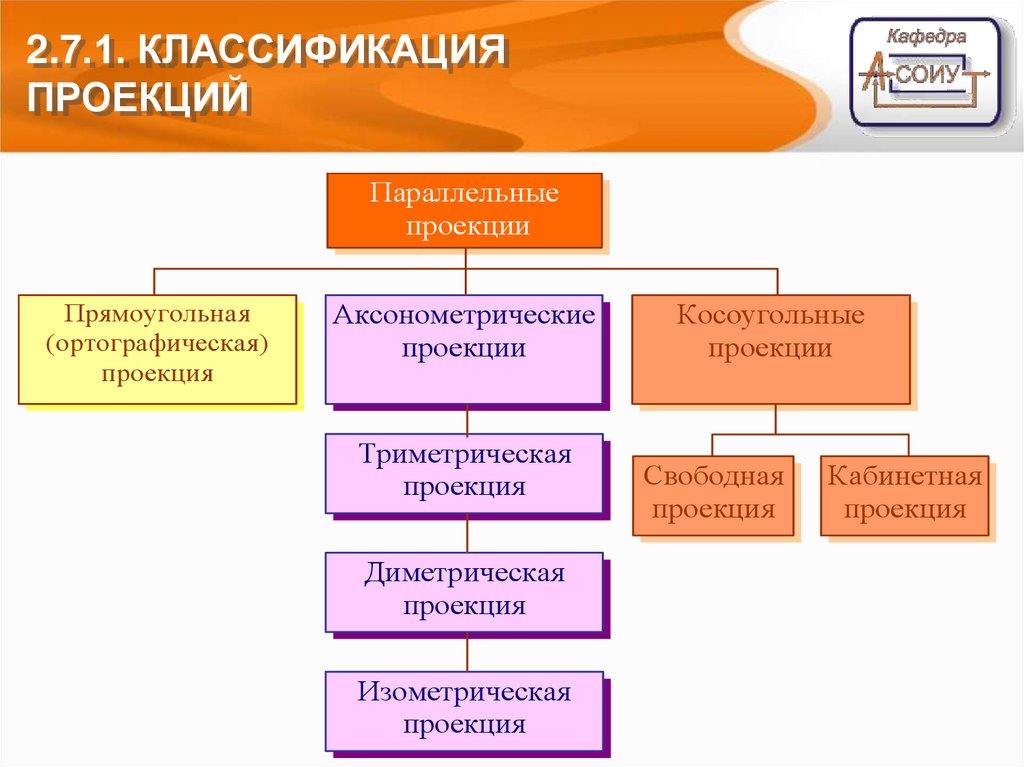
2.7.1. КЛАССИФИКАЦИЯ
ПРОЕКЦИЙ
Параллельные
проекции
Прямоугольная
(ортографическая)
проекция
Аксонометрические
проекции
Триметрическая
проекция
Диметрическая
проекция
Изометрическая
проекция
Косоугольные
проекции
Свободная
проекция
Кабинетная
проекция

6.

2.7.2. ОРТОГРАФИЧЕСКИЕ
ПРОЕКЦИИ
Ортографические проекции (orthographic
view) – это параллельные проекции на
координатные плоскости, линии проецирования у
которых параллельны оси, перпендикулярной к
координатной плоскости, которая выбрана в
качестве картинной, т.е. картинная плоскость
совпадает с одной из координатных плоскостей.
[x y z 1] P(z=0) = [x y 0 1],
1
0
x y z 1
0
0
0
1
0
0
0
0
0
0
0
0
x y 0 1 .
0
1
1
0
P
( z 0) 0
0
0
1
0
0
0
0
0
0
0
0
.
0
1

7.

2.7.3. АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
Аксонометрической проекцией (axonometric
view) называют параллельную проекцию на
картинную плоскость, расположенную под углом к
координатным плоскостям.
Различают три вида аксонометрии:
триметрия (trimetric axonometry) – нормаль к
картинной плоскости образует разные углы с
координатными осями;

8.

2.7.3. АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
диметрия (dimetric axonometry) – нормаль к
картинной плоскости образует два
взаимосвязанных угла с координатными ортами
(длины двух ортов равны);
изометрия (isometric axonometry) – нормаль к
картинной плоскости образует строго
определенные углы со всеми координатными
ортами (длины всех трех ортов равны).
SCEN=ROX( ) ROY( ) P(Z=o)

9.

2.7.3. АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
cos
0
sin sin cos
SCEN
sin cos sin
0
0
0
0
0
0
0
0
.
0
1
Вид орта Оrt’x: [1 0 0 1] SCEN = [cos 0 0 1]
Вид орта Оrt’y: [sin sin cos 0 1]
Вид орта Оrt’z: [sin sin cos 0 1]
Диметрия: орты Оrt’x, Оrt’y искажаются одинаково,
то есть (длина Оrt’x)=(длина Оrt’у).

10.

2.7.3. АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
(длина Оrt’x)2 = cos2 ;
(длина Оrt’y)2 = sin2 sin2 + cos2 .
Из этих уравнений можно найти взаимосвязь между
и :
cos2 = sin2 sin2 + cos2 ;
(1 – sin2 ) = sin2 (1 – cos2 ) + cos2 ;
sin2 = tg2 .
Изометрия: все оси искажаются одинаково, то
есть
(длина Оrt’x) = (длина Оrt’у) = (длина Оrt’z).
(длина Оrt’z)2 = sin2 cos2 + sin2 .

11.

2.7.3. АКСОНОМЕТРИЧЕСКИЕ
ПРОЕКЦИИ
Приравнивания первый и второй орты:
sin2 sin2 + cos2 = cos2 ;
1 – sin2 = sin2 – sin2 cos2 + cos2 ;
sin2 = sin2 cos2 . (*)
первый и третий:
sin2 cos2 + sin2 = cos2 ;
1 – sin2 = sin2 – cos2 cos2 + cos2 ;
sin2 = cos2 cos2 . (**)
Приравнивая последние полученные уравнения (*)
и (**), получим:
cos2 cos2 = sin2 cos2 ; cos2 = sin2 .
1 2
1
sin 1 sin 2
2
2
1
sin
3
2
1
sin
2

12.

2.7.4. КОСОУГОЛЬНЫЕ
ПРОЕКЦИИ
Косоугольная проекция (skew-angle
axonometry) – это параллельная проекция, у
которой проецирующие прямые падают на
картинную плоскость под углом, отличным от
прямого угла, а картинная плоскость параллельна
координатной плоскости.
1
0
M
XOY P
x
0
0
1
P
y
0
0 0
0 0
.
0 0
0 1

13.

2.7.4. КОСОУГОЛЬНЫЕ
ПРОЕКЦИИ
Свободная проекция (free axonometry) – это
параллельная проекция, когда наблюдатель
смотрит на объект под углом 45 , а картинная
плоскость параллельна координатной плоскости.
После проецирования: Оrt’z = [Px Py 0 1]
1
2
2
Px Py
Px Py 1
2

14.

2.7.4. КОСОУГОЛЬНЫЕ
ПРОЕКЦИИ
Кабинетная проекция (cabinet projection) – это
параллельная проекция, когда наблюдатель
смотрит на объект под углом 45 , а картинная
плоскость параллельна координатной плоскости и
длина орта не лежащего в плоскости проекции в
два раза меньше.
1
0
0 0
M
0
1
кабXOY
cos
2
4
0
1
1
cos
2
4
0
0 0
0 0
0 1
.

15.

2.7.5. ПЕРСПЕКТИВНЫЕ
ПРОЕКЦИИ
Центральная проекция (central projection) –
это проекция, проецирующие лучи в которой
выходят из одной точки, не лежащей в
бесконечности.
y
X x1
Y y1
Z z1
,
x 2 x1 y 2 y1 z 2 z1
2
1
C(0,0,с)
z
3 (x’,y’,0)
x
x , 0 y, 0 0 с
x 0
y 0 z c

16.

2.7.5. ПЕРСПЕКТИВНЫЕ
ПРОЕКЦИИ
x
c
y
c
;
;
x z c y z c
c
c
x x
; y y
,
z c
z c
x x
1
z
1
c
; y y
1
z
1
c
;
z ' 0.
z
[x y z 1] [Persp] = [x y 0 1 ]
c

17.

2.7.5. ПЕРСПЕКТИВНЫЕ
ПРОЕКЦИИ
x y z 1
1
0
0
1
0
0
0
0
0
0
0
0
1 0 0
0 1 0
0
0
z
1 x y 0 1 .
c
c
1
0
0
Persp XOY
1.
0 0 0
c
0 0 0 1

18.

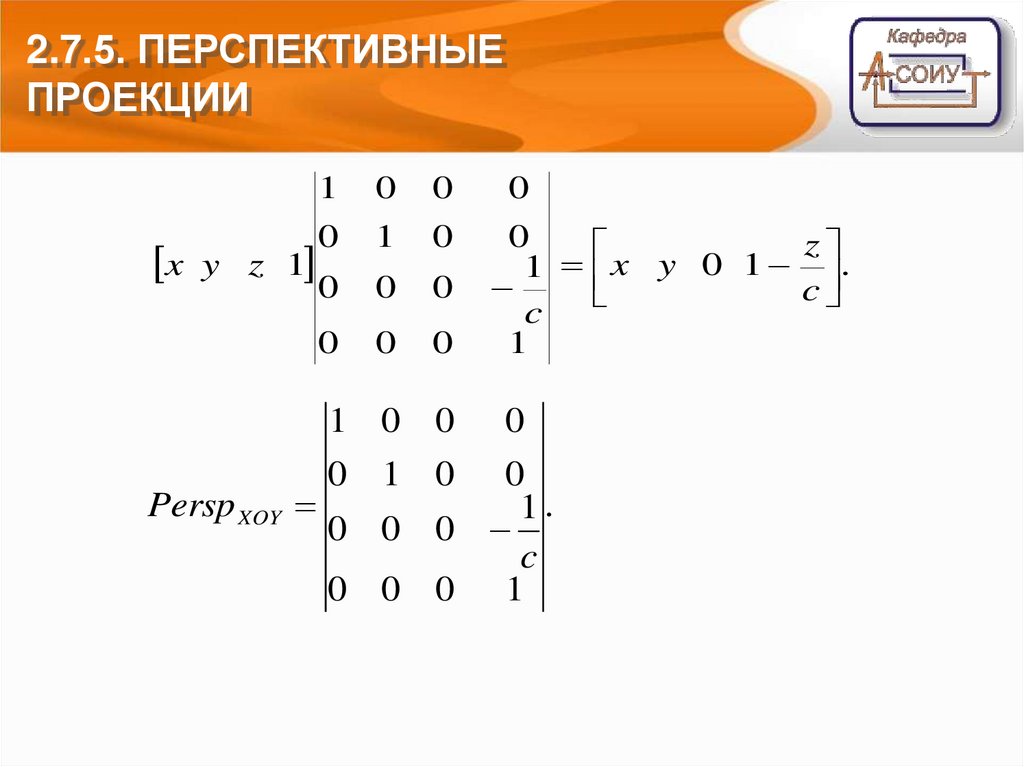
2.7.5. ПЕРСПЕКТИВНЫЕ
ПРОЕКЦИИ
Матрица перспективного преобразования (без
проекции на плоскость XOY)
1 0 0
0 1 0
0
0
PP
1;
0 0 1
c
0 0 0 1
Общая матрица
PP
1
0
0
0
1
0
0
0
1
0
0
0
1
c
x
1
c .
y
1
c
z
1

19.

2.8. ЛАБОРАТОРНАЯ РАБОТА №2
Цель работы: получить навыки работы с аффинными
преобразованиями в пространстве и построения
проекций на экране.
Основная задача работы: Создать программу реализации
демонстрации построения проекций и аффинных
преобразований в пространстве.
Ключевые понятия, которые необходимо знать:
аффинные преобразования, однородные координаты,
взаимооднозначное отображение, преобразование координат,
принцип отделения данных от сценария, пучок проецирующих
прямых, точка схода, однородные координаты, центральные и
параллельные проекции, ортографическая проекция,
аксонометрия, триметрия, диметрия, изометрия, косоугольная
проекция, кабинетная проекция, свободная проекция.

20.

2.8. ЛАБОРАТОРНАЯ РАБОТА №2
Задание на проведение лабораторной работы:
1. Изучить свойства аффинных преобразований.
2. Изучить построение проекций трехмерных тел
на плоскости.
3. Разработать (или усовершенствовать) алгоритм
построения аффинных преобразований в
пространстве.

21.

2.8. ЛАБОРАТОРНАЯ РАБОТА №2
На оценку «удовлетворительно»
4. Разработать программу, демонстрирующую все
частные случаи аффинных преобразований в
пространстве. Программа также должна
демонстрировать каждую проекцию для
тетраэдра, октаэдра, гексаэдра и произвольной
фигуры (не менее 10 вершин) координаты
которых можно задавать в программе.

22.

2.8. ЛАБОРАТОРНАЯ РАБОТА №2
На оценку «хорошо»
4. Разработать программу, демонстрирующую все частные
случаи аффинных преобразований в
мультипликационном сценарии и по отдельности.
Программа должна демонстрировать каждую проекцию
для любой объемной фигуры (предусмотреть
статический режим – без движения). Данные о фигурах
программа должна считывать из текстовых файлов.
Необходимо подготовить данные о платоновых телах и
одной (или более) произвольной объемной фигуре с
количеством вершин не менее 15.

23.

2.8. ЛАБОРАТОРНАЯ РАБОТА №2
На оценку «отлично»
4. Разработать программу, демонстрирующую все
проекции четырехмерного пространства на
плоскость. Предусмотреть демонстрацию
частного случая аффинных преобразований для
фигур – поворота. Данные о фигурах программа
должна считывать из текстового файла.
Необходимо подготовить данные о тессеракте –
четырехмерном кубе.

24.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Задача 1. Создайте сценарий аффинных
преобразований поворота на 45 правильного
треугольника вокруг его центра тяжести и переноса
его в третью координатную четверть из первой
четверти (чтобы одна из его вершин касалась
любой координатной оси). Заданы координаты
одной вершины (10, 10) (ближайшей к началу
координат) и сторона – 10.

25.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
B
Y
10
10
A
C
X
10

26.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
SCEN = T1 R( ) T2
Шаг 1. Перенос точки – центра тяжести в начало
координат (и точек А, B, C).
B
Точка M имеет координаты:
Y
x = 10 + 5, 3 1
10
y = 10 + 10
M
2
3
10
A
Параметры матрицы T1:
5 3
x1 = -15, y1 = 10
3
C
X
10

27.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после переноса:
Точка А: до переноса (10, 10)
5 3
после переноса (-5,
)
3
Точка B: до переноса (15, 10 5 3 )
10 3
после переноса (0,
)
3
Точка C: до переноса (20, 10)
5 3
после переноса (5,
)
3

28.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Шаг 2. Поворот на угол 45°.
Матрица R( ) имеет вид
2
R( ) 2
2
2
2
2 .
2
2

29.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после поворота:
5 3
Точка А: до поворота (-5,
)
3
после поворота
2 5 3 2
2 5 3 2
5
,
5
2
3
2
2
3
2
5 2 5 6 5 2 5 6
,
2
6
2
6

30.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после поворота:
10 3
Точка B: до поворота (0,
)
3
после поворота
10 3 2 10 3 2
,
3
2
3
2
5 6 5 6
,
3
6

31.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после поворота:
5 3
Точка C: до поворота (5,
)
3
после поворота
2 5 3 2
2 5 3 2
5
,
5
2
3
2
2
3
2
5 2 5 6 5 2 5 6
,
2
6
2
6

32.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Шаг 3. Перенос треугольника, так чтобы вершина
С касалась оси OY.
Параметры матрицы T2:
x2 = - (координата х точки С после поворота),
y2 = -20
5 2 5 6
x2
, y2 20
2
6

33.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после переноса:
Точка А: до переноса 5 2
5 6 5 2 5 6
,
2
6
2
6
после переноса
5 2 5 6 5 2 5 6 5 2 5 6
,
20
2
6
2
6
2
6
10 2 5 2 5 6
,
20
2
2
6

34.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после переноса:
Точка B: до переноса
после переноса
5 6 5 6
,
3
6
5 6 5 2 5 6 5 6
,
20
3
2
6
6
5 2 15 6 5 6
,
20
2
6
6

35.

ПОДГОТОВКА К КОНТРОЛЬНОЙ
РАБОТЕ №1
Координаты точек треугольника после переноса:
5 2 5 6 5 2 5 6
Точка C: до переноса
,
2
6
2
6
после переноса
5 2 5 6 5 2 5 6 5 2 5 6
,
20
2
6
2
6
2
6
5 2 5 6
0,
20
2
6