Теория кривых. Эволюта и Эвольвента

1. ТЕОРИЯ КРИВЫХ

Эволюта и эвольвента
плоской кривой

2. Эволюта

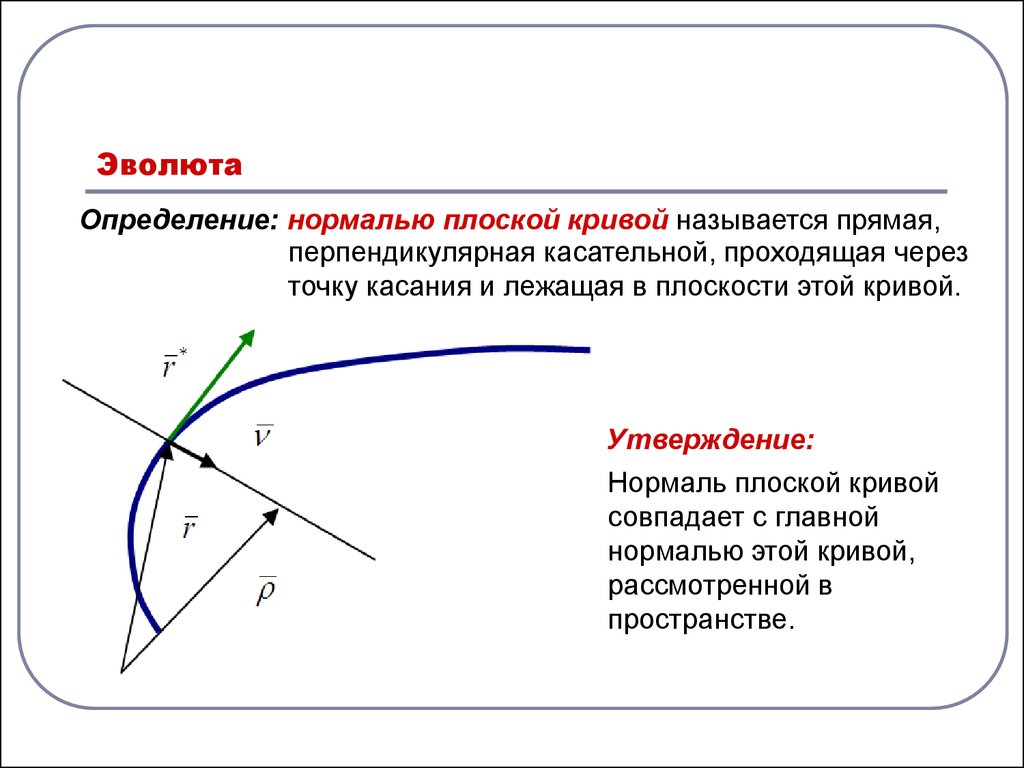
Определение: нормалью плоской кривой называется прямая,
перпендикулярная касательной, проходящая через
точку касания и лежащая в плоскости этой кривой.
Утверждение:
Нормаль плоской кривой
совпадает с главной
нормалью этой кривой,
рассмотренной в
пространстве.

3. Эволюта

Fx ; Fy
-направлен вдоль нормали плоской кривой с неявным
уравнением.
x y
,
(43)
Fx
Fy
(43) – уравнение нормали плоской кривой, где (x; y) – точка,
лежащая на кривой.
x ; y
нормали
x x y y 0
(44) – уравнение нормали плоской кривой, заданной
параметрическими уравнениями.
(44)

4. Уравнение эволюты

Определение: огибающая семейства нормалей плоской кривой
называется эволютой.
( r ) r 0
( 44 )
Уравнения (44) и (44’) можно записать в виде:
Продифференцируем это уравнение по t:
r 2 ( r ) r 0
F ( ; ; t ) 0.
(45)
Распишем уравнения (44’) и (45) по координатам и найдем их
решение:
( x) x ( y ) y 0
| (- y ) | ( x )
2
2
( x) x ( y ) y x y | y | x

5. Уравнение эволюты

( x)( x y x y ) y ( x 2 y 2 )
( y )( x y x y ) x ( x 2 y 2 )
x 2 y 2
x y
x y x y
x 2 y 2
y x
x y x y
(46) – параметрические уравнения эволюты.
(46)

6. Эвольвента

Определение: ортогональной траекторией данного семейства
плоских кривых называется кривая, которая
пересекает каждую кривую данного семейства под
прямым углом.

7. Эвольвента

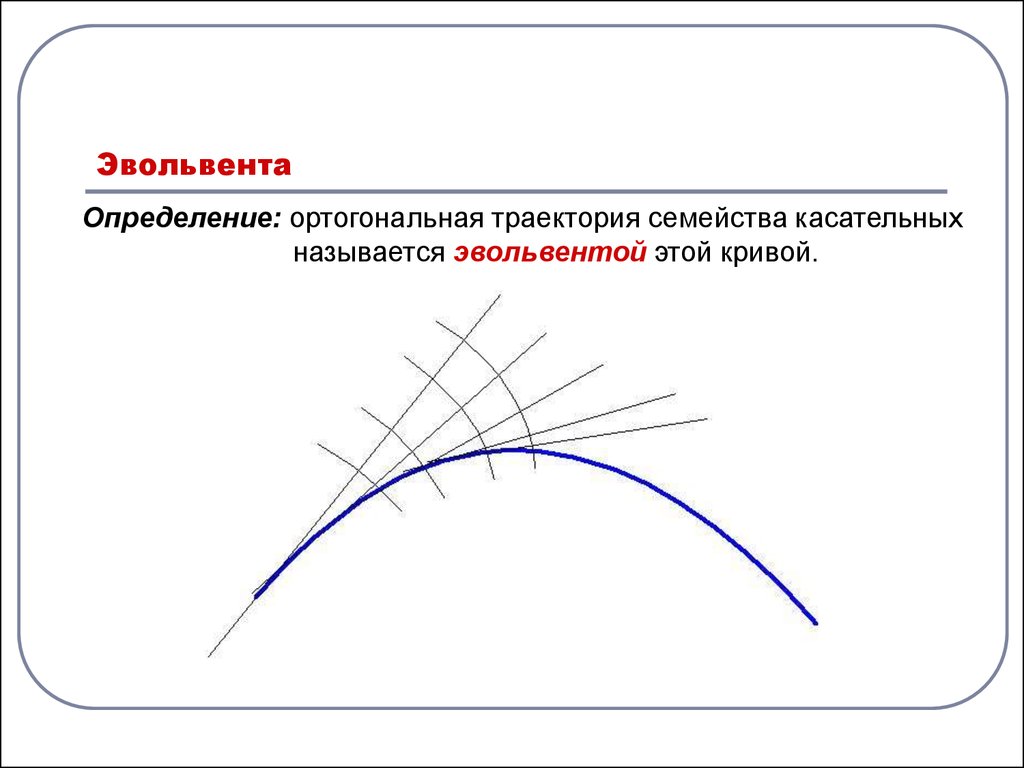
Определение: ортогональная траектория семейства касательных
называется эвольвентой этой кривой.

8. Уравнение эвольвенты

Пусть r r (s ) - уравнение кривой, (s ) - касательный вектор,
- радиус-вектор точек на эвольвенте.
r (s) || r (s)
|
1
1
d ds
s0 s
r (s) (s0 s)
(47) – уравнение эвольвенты.
(47)

9. Натуральные уравнения пространственной кривой

1 r (s) (s1 s)
2 r (s) (s2 s)
2 1 (s2 s1 )
| 2 1 | | s2 s1 |
Утверждение:
2 эвольвенты одной кривой являются эквидистантными линиями.
Натуральные уравнения пространственной кривой.
k k ( s)
( s)
(48) – натуральные уравнения пространственной кривой.
(48)