Похожие презентации:
Тождественные преобразования тригонометрических выражений. 9 класс
1. Тождественные преобразования тригонометрических выражений 9 класс
2.
Тождественные преобразования тригонометрическихвыражений опираются на следующие основные
формулы:
Формулы приведения.
Формулы для тригонометрических функций одного и того
же аргумента.
Формулы сложения аргументов.
Формулы двойного угла.
Формулы половинного аргумента.
Формулы преобразования суммы(разности)
тригонометрических функций в произведение.
Формулы преобразования произведения
тригонометрических функций в сумму( разность).
3.
Формулы понижения степени1 cos 2
cos
2
2
1 cos 2
sin
2
3 cos cos 3
cos 3
4
3 sin sin 3
3
sin
4
2
4.
I способВычислить: 125 (cos8 sin 8 ), åñëè cos 2 0,8.
125 (cos 8 sin 8 ) 125 (cos 4 sin 4 )(cos 4 sin 4 )
125 (cos 2 sin 2 ) (cos 2 sin 2 ) (cos 4 sin 4 )
125 cos 2 (cos 4 sin 4 ) 125 0,8 (cos 4 sin 4 )
1 cos 2 2 1 cos 2 2
1 0.8 2 1 0.8 2
100 [(
) (
) ] 100 [(
) (
) ]
2
2
2
2
100 (0,92 0,12 ) 100 (0,81 0,01) 100 0,82 82
5.
II способВычислить 125 (cos8 sin 8 ) , åñëè cos 2 0,8
:
125 (cos 8 sin 8 ) 125 (cos 4 sin 4 ) (cos 4 sin 4 )
125 (cos 2 sin 2 ) (cos 2 sin 2 ) (cos 4 sin 4 )
125 cos 2 (cos 4 sin 4 ) 125 0,8 (cos 4 sin 4 )
100 (cos 4 sin 4 )
100 [(cos 4 2 sin 2 cos 2 sin 4 ) 2 sin 2 cos 2 ]
100 [(cos 2 sin 2 ) 2 2 sin 2 cos 2 ]
4 sin 2 cos 2
sin 2 2
100 (1
) 100 (1
)
2
2
1 cos 2 2
2 1 0,64
100 (1
) 100 (
) 100 0,82 82
2
2
6.
1sin sin [cos( ) cos( )]
2
1
cos cos [cos( ) cos( )]
2
1
sin cos [sin( ) sin( )]
2
7.
Пример: sin x sin 3x sin 4x sin 8x1
1
[cos( x 3x) cos( x 3x)] [cos( 4 x 8 x) cos( 4 x 8 x)]
2
2
1
1
[cos( 2 x) cos 4 x] [cos( 4 x) cos12 x]
2
2
1
1
(cos 2 x cos 4 x cos 4 x cos 12 x) (cos 2 x cos12 x)
2
2
1
2 x 12 x
2 x 12 x
( 2 sin
sin
) sin( 5 x) sin 7 x
2
2
2
sin 5x sin 7 x
8.
Доказать тождество:sin( ) sin( ) sin 2 sin 2
sin( ) sin( ) (sin cos sin cos )
(sin cos sin cos ) sin 2 cos 2 sin 2 cos 2
sin 2 (1 sin 2 ) sin 2 (1 sin 2 )
sin 2 sin 2 sin 2 sin 2 sin 2 sin 2 sin 2 sin 2
9. 1 способ
2sin (
sin(
2
2 ) sin (
2
2
2
2
sin sin 4
2
2 )
2 ) sin(
2
2
Применили формулу
sin( ) sin( ) sin sin
2
2
2
2 )
10. 2 способ
sin 2 (2
2 ) sin 2 (
2
2 )
)
2
sin(
)
2
sin(
)
2
sin(
)
2
sin(
2
2
2
2
2 sin 2
2 sin 2
2
2
2
2
2
2
2
2
2 sin 2 cos
2
2 sin
cos 2
cos 2
2
2
2
2
2
2
2
2
2
cos 2 sin 4 sin
11.
3 способ2
sin (
2
2 ) sin (
2
2
2 )
2 ) 1 cos 2( 2 )
2
2
2
2
1 cos( 4 ) 1 cos( 4 ) cos( 4 ) cos( 4 )
2
2
4 4
4 4
2 sin
sin
2
2
2
sin sin( 4 ) sin sin 4
1 cos 2(
12.
sin ( ) sin ( )8 2
8 2
2
sin(
8
2
2
8
) sin(
2
8
2
sin sin
sin
4
2
2
8
2
)
13.
Упроститеcos 2 2 sin( 30 ) sin( 30 )
cos 2 sin 2 2(sin 2 sin 2 30 )
1
cos sin 2 sin
2
1
1 1
2
2
cos sin 1
2
2 2
2
2
2
14.
1Доказать тождество: sin sin( 60 ) sin( 60 ) sin 3
4
0
0
sin sin( 600 ) sin( 600 ) sin (sin 2 600 sin 2 )
1
3
1
2
3
sin ( sin ) (3 sin 4 sin ) sin 3
4
4
4
15.
Аналогично доказываются тождества:1
cos cos(60 ) cos(60 ) cos 3
4
tg tg(600 ) tg(600 ) tg3
0
0
ctg ctg(600 ) ctg(600 ) ctg3
Пользуясь этими тождествами легко доказать, что:
1
3
0
sin 20 sin 40 sin 80 sin 60
4
8
0
0
0
1
3
0
cos10 cos 50 cos 70 cos 30
4
8
0
0
0
tg60 tg540 tg660 tg180
16.
Вычислить:tg 200 tg 400 tg600 tg800 (tg 200 tg 400 tg800 ) tg600 tg600 tg600
3 3 3
Второй способ:
0
0
0
sin
20
sin
40
sin
80
tg 200 tg 400 tg600 tg800
3
0
0
0
cos 20 cos 40 cos 80
1
8 3 cos100 sin 200 sin 400 8 3 cos100 (cos 200 cos 600 )
2
1
1
0
0
0
0
0
8 3 cos10 ( cos 20 ) 4 3 cos10 cos 20 2 3 cos10
2
4
3 1
1
0
0
0
cos100 ) 2 3 cos100
4 3 ( (cos 30 cos10 )) 2 3 cos10 4 3 (
4 2
2
3 2 3 cos100 2 3 cos100 3
17.
Вычислить: cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 8401
cos 24 cos 36 cos 84 cos 720
4
1
0
0
0
cos12 cos 48 cos 72 cos 360
4
0
0
0
cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840
1
1
0 1
0
0
0
0 1
cos 72 cos 36 cos 60 cos 72 cos 36
4
4
16
2
cos 720 cos 360 cos 720 2 cos 360 sin 360 cos 720 sin 720
0
0
32
2 32 sin 36
64 sin 36
1
sin 1440
sin 360
sin( 1800 360 )
0
0
0
128
128 sin 36
128 sin 36
128 sin 36
18.
Вычислить: cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840cos 120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840
0
0
2 sin 120 cos120
2
sin
36
cos
36
1
0
0
0
0
0
cos 24
cos 48 cos 72 cos(90 6 )
0
0
2 sin 12
2 sin 36
2
2 sin 240 cos 240 2 sin 720 cos 720 cos 480 sin 60
0
0
4 8 sin 12 sin 36
2 sin 480 cos 480 sin 1440 sin 60 sin 960 sin 360 sin 60
0
0
0
2 32 sin 12 sin 36
64 sin 12 sin 36
sin 120
1
2 cos 60 sin 60
0
0
128 sin 12 128
2 64 sin 12
19.
Примеры преобразований тригонометрических выраженийчасто встречающиеся или имеющие необычный подход в решении
Пример1:
2sin20 0 cos20 0 cos40 0 cos80 0 2 sin 800 cos 800
0
0
0
cos20 сos40 cos80
2sin20 0
2 4 sin 200
sin 1600 sin( 1800 200 ) sin 200 1
0
0
0
8 sin 20
8 sin 20
8 sin 20
8
Способ 2
1
1 1 1
cos20 0 сos40 0 cos80 0 cos 60
4
4 2 8
Применили формулу
cos cos(60 ) cos(60 )
1
cos 3
4
20.
Пример 2:tg10 tg30 tg50...tg890
tg890 tg(900 10 ) сtg10
tg870 tg(900 30 ) сtg30
tg850 tg(900 50 ) сtg50
и т.д., кроме этого:
tg 470 tg(900 430 ) сtg 430
умножим:
tg10 tg890 tg10 сtg10 1
все попарные произведения дают 1, а tg450=1. следовательно все
выражение равно 1.
21.
Вычислить:1 cos 6 1 cos 2 1
cos 3 cos 1 cos 4 cos 2
(cos 6 cos 2)
2
2
2
2
2
1 1
1 1
1
1
cos 6 cos 2 cos 6 cos 2 1
2 2
2 2
2
2
22. Преобразовать в произведение.
35
2 cos ( ) 3 cos( ) 1
2 2
2
2
2 sin
2
2 sin
2
sin
2
2
2
2
3 sin 1
3 sin cos
cos
2
2
2
2
sin
2
2
3 sin
3
1
cos 3 sin 2( sin cos )
2
2
2(sin cos 30 cos sin 30 ) 2 sin( 30 )
23.
34
Вычислить: sin( arctg arcctg ).
4
3
Воспользуемся формулами перехода от одной обратной
тригонометрической функции к другой:
x
1
1
arctg x arcsin
arccos
arcctg
x
1 x2
1 x2
åñëè 0 x ,
3
3
4
тогда arctg arcсtg , получим sin (2arсtg )
4
4
3
3
34
3 5
3
arсtg arcsin
arcsin arcsin
4
4 4
5
1 9 16
3
3
3
4
sin(2 arcsin ), ïóñòü arcsin , òîãäà sin , cos , I ÷åòâ.
5
5
5
5
3
3 4 24
sin(2 arcsin ) sin 2 2 sin cos 2
5
5 5 25



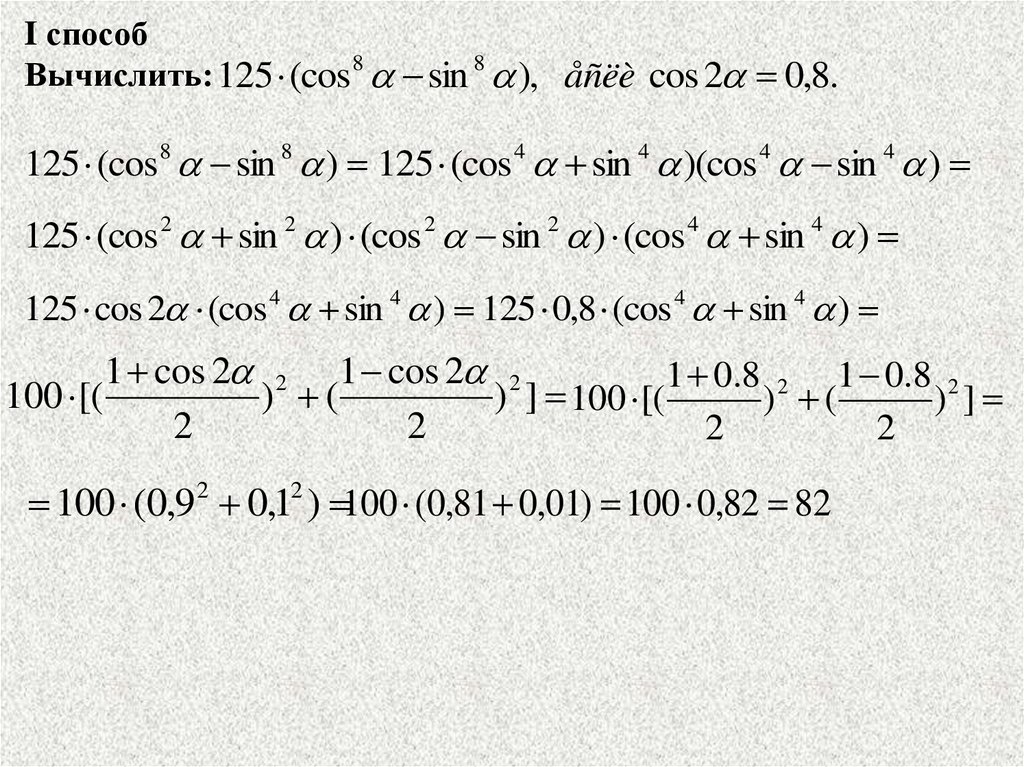




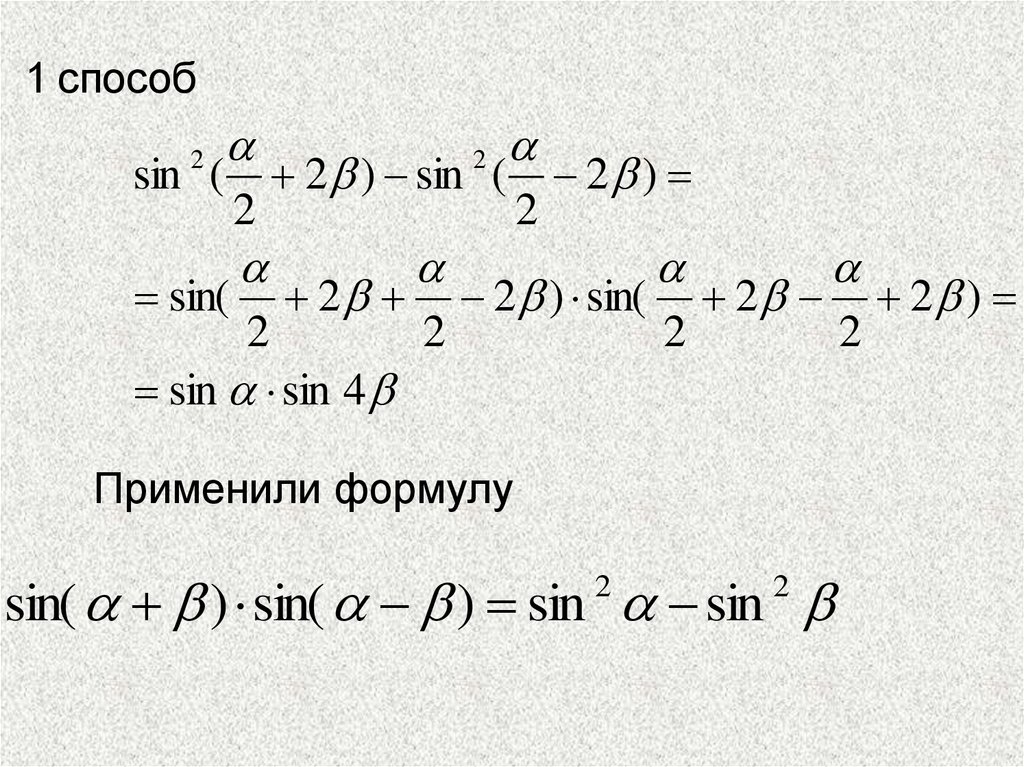

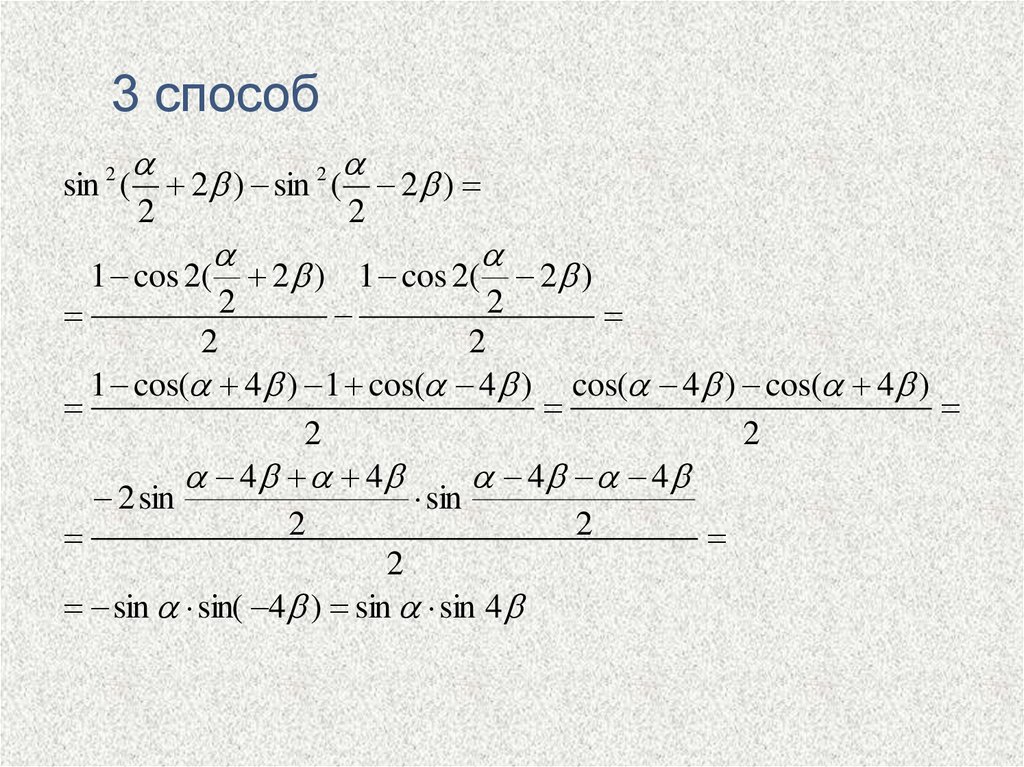


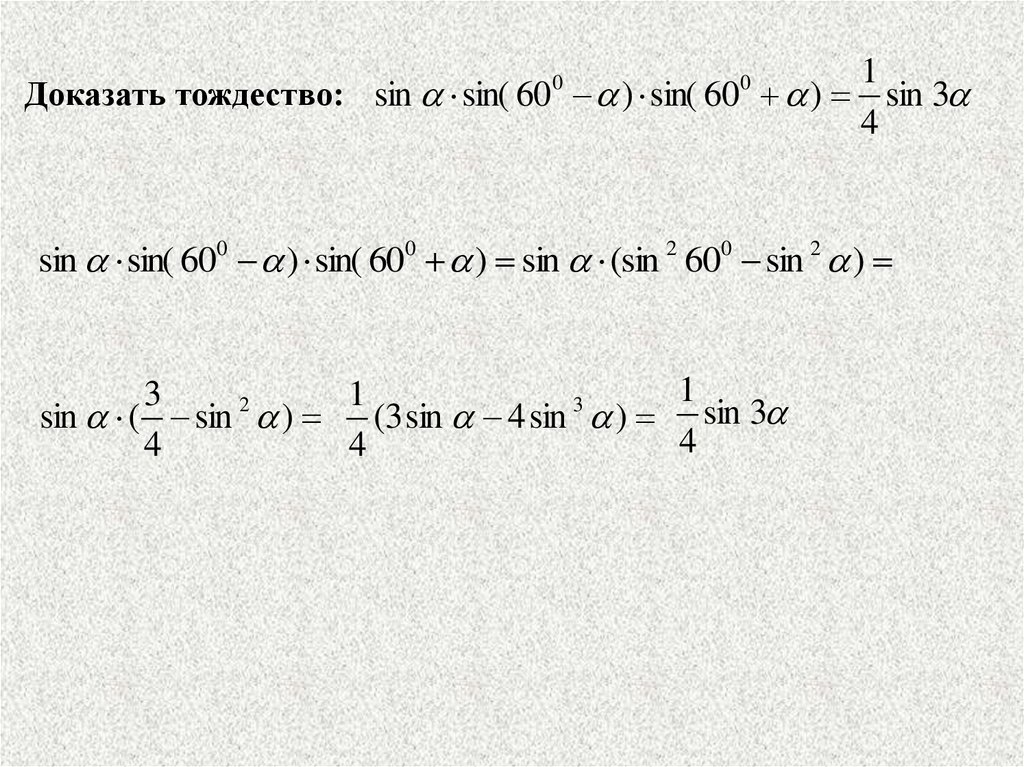

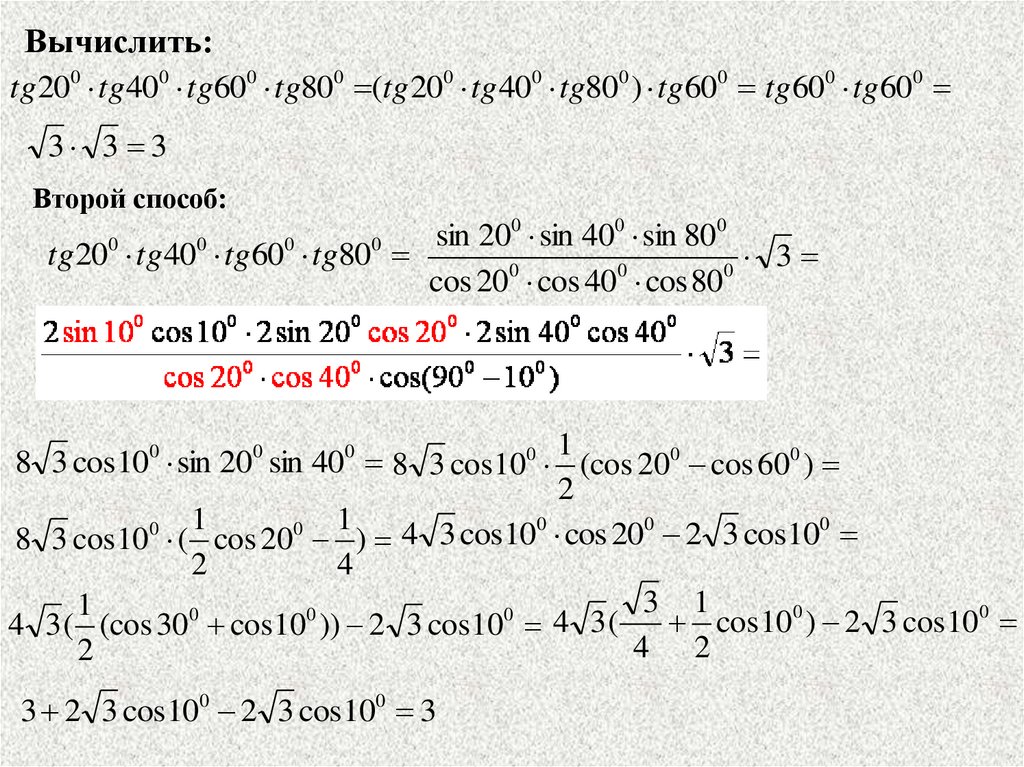

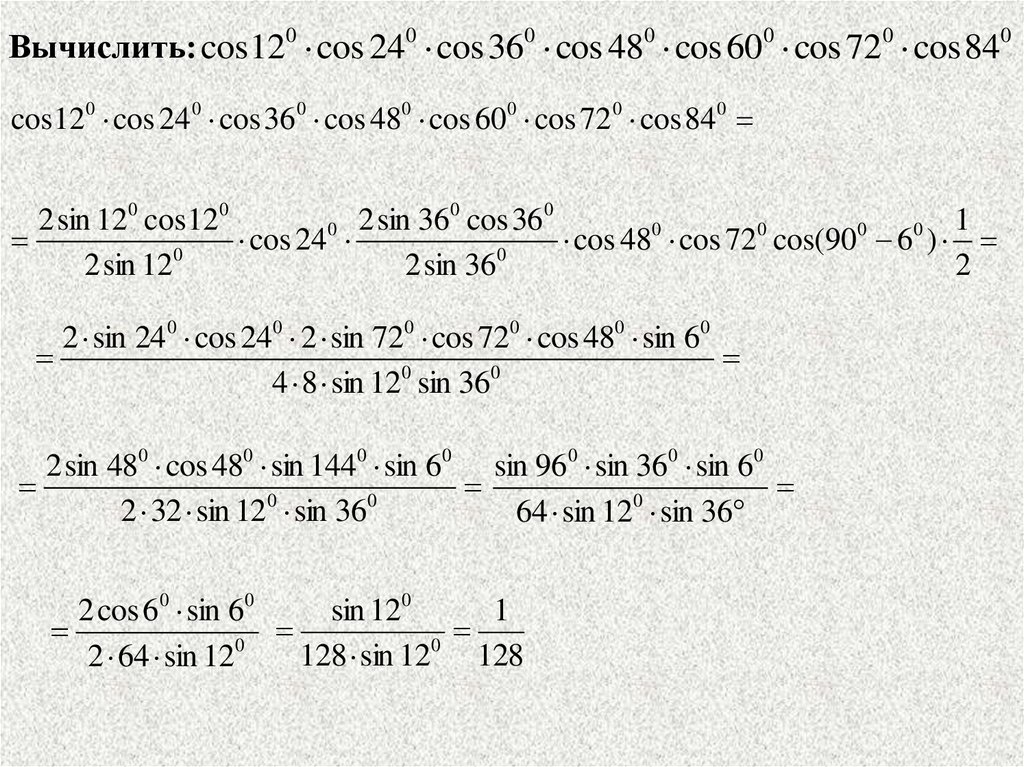






 Математика
Математика








