Свойства касательных к окружности. 7 класс

1.

Касательная к
окружности

2.

Цели урока:
уметь строить касательную к
окружности;
знать понятия касательной, точки
касания, отрезков касательных,
проведённых из одной точки;
понимать свойство касательной и её
признак и показать их применение при
решении задач;

3.

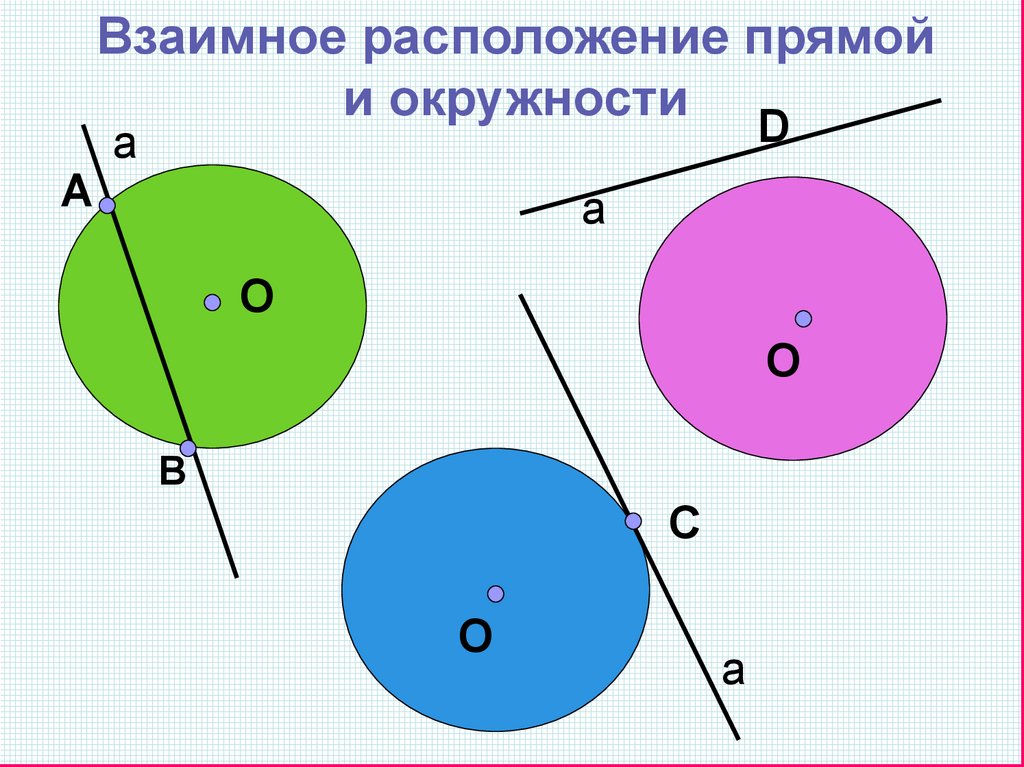
Взаимное расположение прямой
и окружности
А
D
а
а
О
О
В
С
О
а

4.

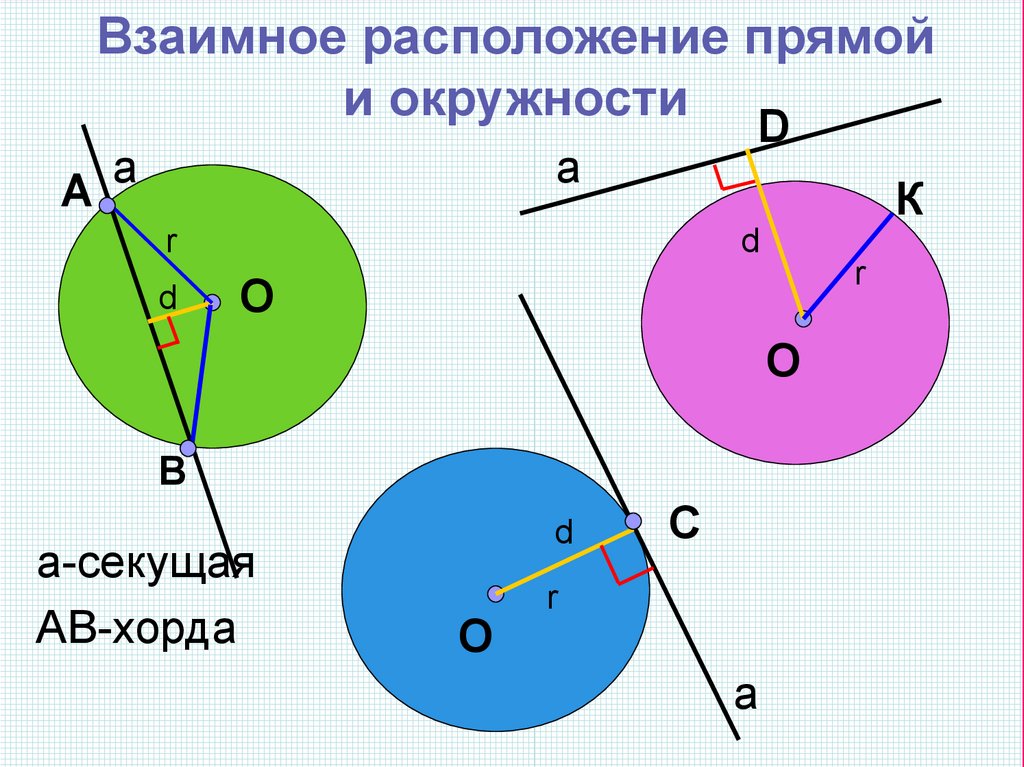
Взаимное расположение прямой
и окружности
А
а
D
а
К
r
d
d
r
О
О
В
а-секущая
АВ-хорда
d
О
С
r
а

5.

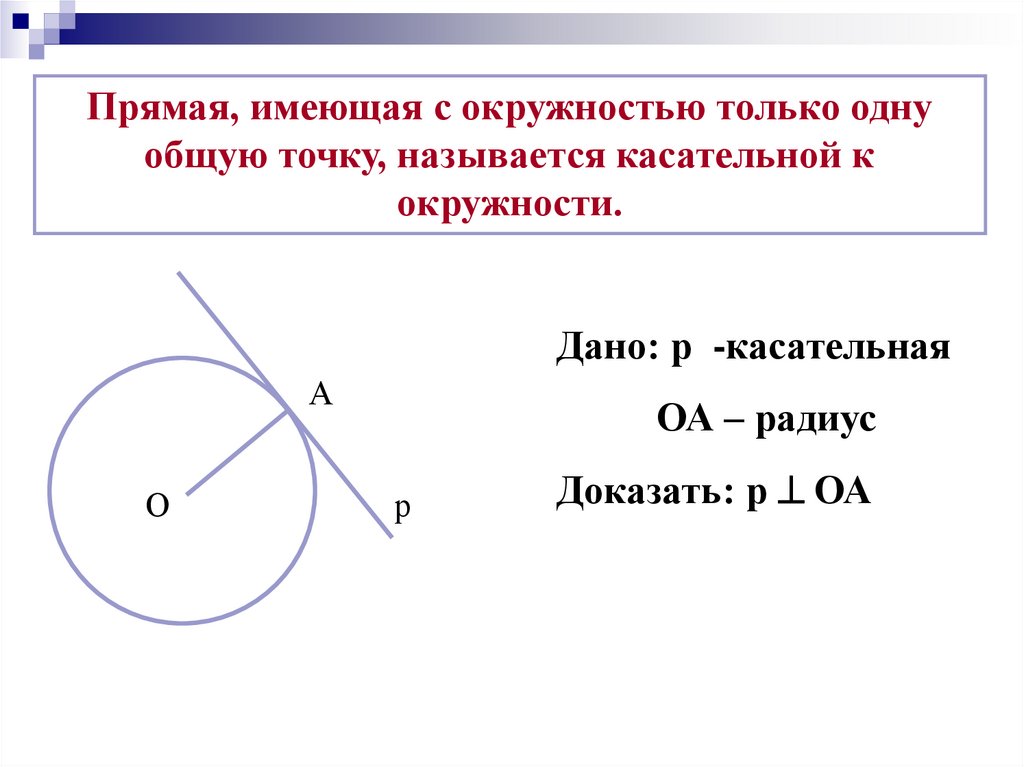
Прямая, имеющая с окружностью только одну
общую точку, называется касательной к
окружности.
Дано: р -касательная
А
О
ОА – радиус
р
Доказать: р ОА

6.

Теорема 1
Если расстояние от центра окружности до прямой
равно радиусу окружности, то эта прямая
является касательной к окружности.
Доказательство. Пусть расстояние
от центра О окружности до прямой
а равно радиусу R окружности.
Опустим из центра О
перпендикуляр ОА на эту прямую.
Тогда ОА = R. Для любой другой
точки B на прямой а наклонная ОB
будет больше перпендикуляра ОА
и, следовательно, больше R. Таким
образом, расстояние от любой
точки прямой а, отличной от А, до
центра О больше R. Значит,
прямая а и окружность имеют одну
общую точку А, т.е. прямая
касается окружности.

7.

Теорема 2
Касательная к окружности перпендикулярна к радиусу,
проведенному в точку касания.
Докажите самостоятельно.

8.

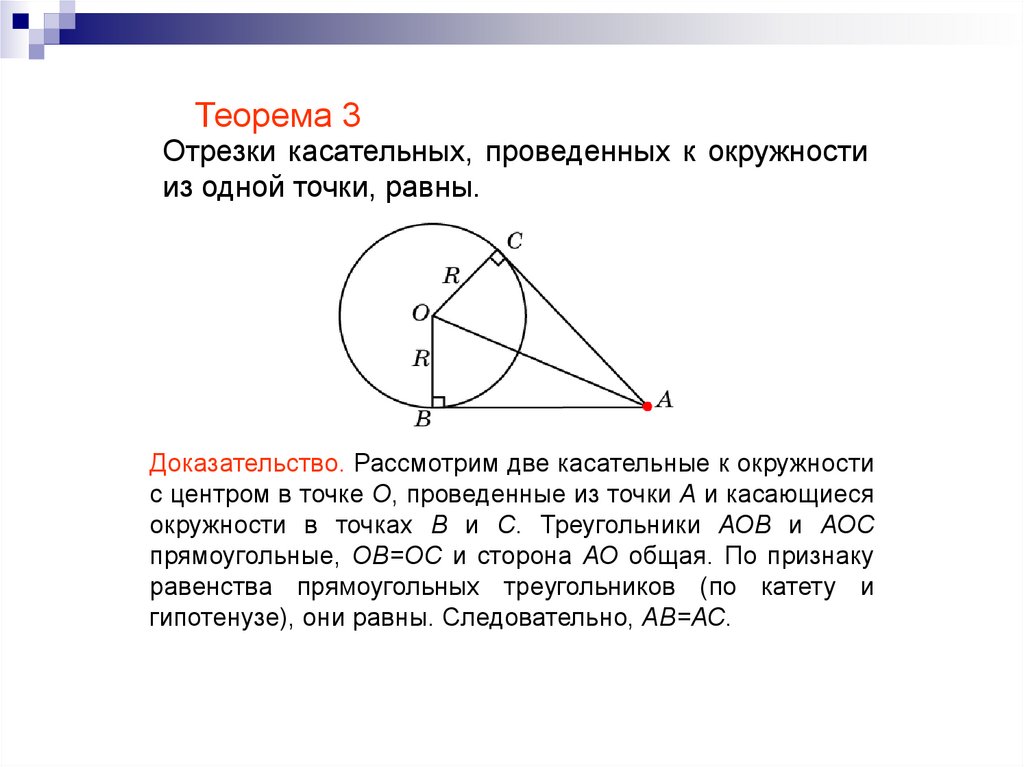
Теорема 3
Отрезки касательных, проведенных к окружности
из одной точки, равны.
Доказательство. Рассмотрим две касательные к окружности
с центром в точке О, проведенные из точки А и касающиеся
окружности в точках В и С. Треугольники АОВ и АОС
прямоугольные, ОВ=ОС и сторона АО общая. По признаку
равенства прямоугольных треугольников (по катету и
гипотенузе), они равны. Следовательно, АВ=АС.

9.

Вопрос 1
Какая прямая называется касательной к
окружности?
Ответ: Касательной к окружности
называется прямая, имеющая с
окружностью только одну общую точку.

10.

Вопрос 2
В
каком
случае
окружности?
прямая
касается
Ответ: Если расстояние от центра
окружности до прямой равно радиусу
окружности.

11.

Вопрос 3
Какой угол образуют касательная к
окружности и радиус, проведенный в точку
касания?
Ответ: 90о.

12.

Вопрос 4
Что
можно
сказать
об
отрезках
касательных к окружности, проведенных из
одной точки?
Ответ: Они равны.

13.

Самостоятельная работа
1. КМ и КN - отрезки
касательных,
проведённых из точки К
к окружности с центром
в точке О. Найдите КМ
и КN, если ОК=12 см, а
<МОN =1200
2. Диагонали ромба
АВСК пересекаются в
точке О. Докажите, что
прямая ВК касается
окружности с центром в
точке А и радиусом ОС.
1. Найдите отрезки
касательных АВ и АС,
проведённых из точки А
к окружности радиуса
r=9 см, <ВАС=1200
2. В равнобедренном
АВС с основанием АС
проведена медиана ВК.
Докажите, что прямая
ВК касается окружности
с центром С и радиусом,
равным АК.