Критерии прочности при изгибе. Распространение критериев прочности на случай циклического нагружения

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Динамика, прочность машин и сопротивление материалов»
Дисциплина «Механика композиционных материалов»
Критерии прочности при изгибе.
Распространение критериев
прочности на случай циклического
нагружения
д.т.н., профессор
Полилов А.Н.
Москва, 2021

2.

Подтемы:
С3.3.1. Критерий расслоения композитных
балок при изгибе.
С3.3.2. Критерий межслойной прочности при
циклическом изгибе.
С3.3.3. Масштабный эффект при изгибе.

3.

Линейный критерий
межслойного разрушения
композитных балок при
изгибе.

4.

Линейное
распределение
нормальных
напряжений
и
параболическое распределение касательных напряжений по
высоте изгибаемого образца при поперечном, трехточечном
изгибе:
max
max
h
max 2 L
3 PL
3P
max
2
2 th
4 th
- отношение показывает, что в коротких
образцах при изгибе касательные напряжения
могут раньше достигнуть предела прочности, чем
нормальные, и при этом происходит межслойное
разрушение от сдвига. Этот вид разрушения
позволяет оценивать межслойную сдвиговую
прочность
(иногда
говорят:
прочность
межслоевого сдвига – interlaminar shear strength).

5.

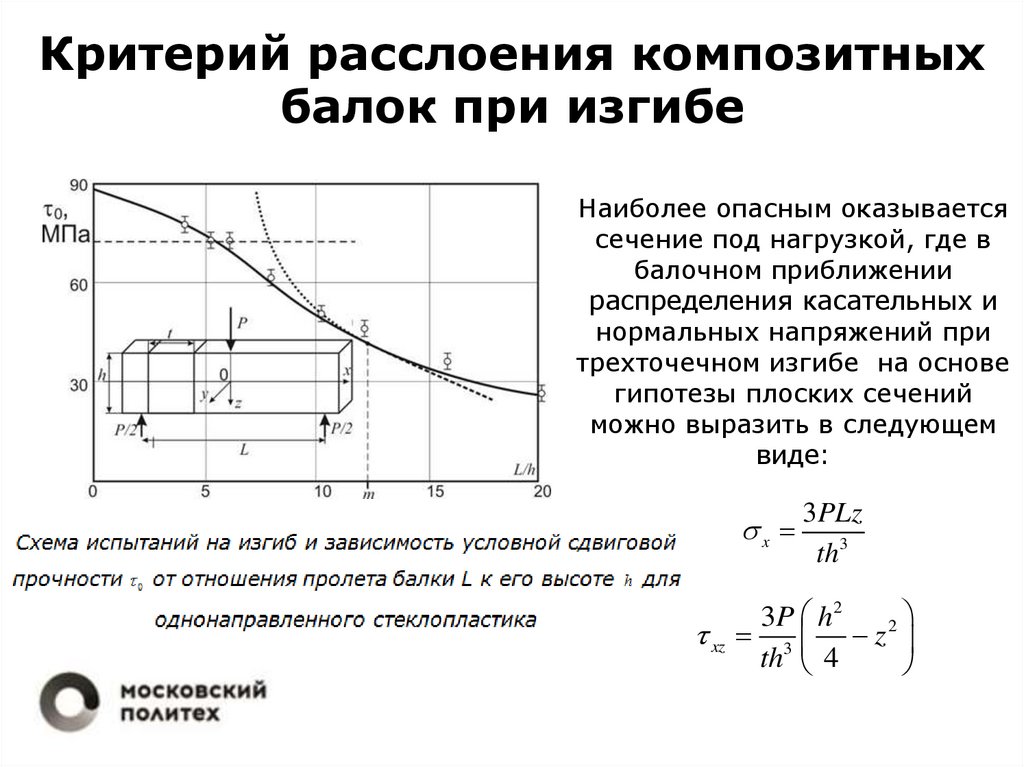
Критерий расслоения композитных
балок при изгибе
Наиболее опасным оказывается
сечение под нагрузкой, где в
балочном приближении
распределения касательных и
нормальных напряжений при
трехточечном изгибе на основе
гипотезы плоских сечений
можно выразить в следующем
виде:
x
3PLz
th3
3P h 2
2
xz 3 z
th 4

6.

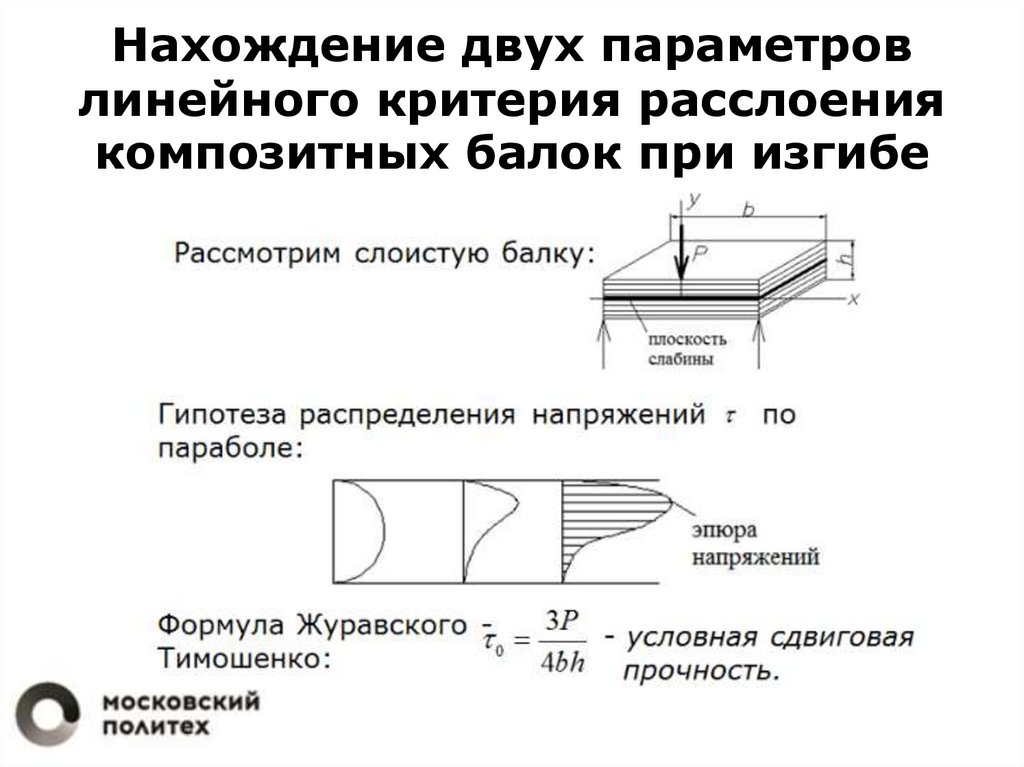
Нахождение двух параметров
линейного критерия расслоения
композитных балок при изгибе

7.

8.

9.

10.

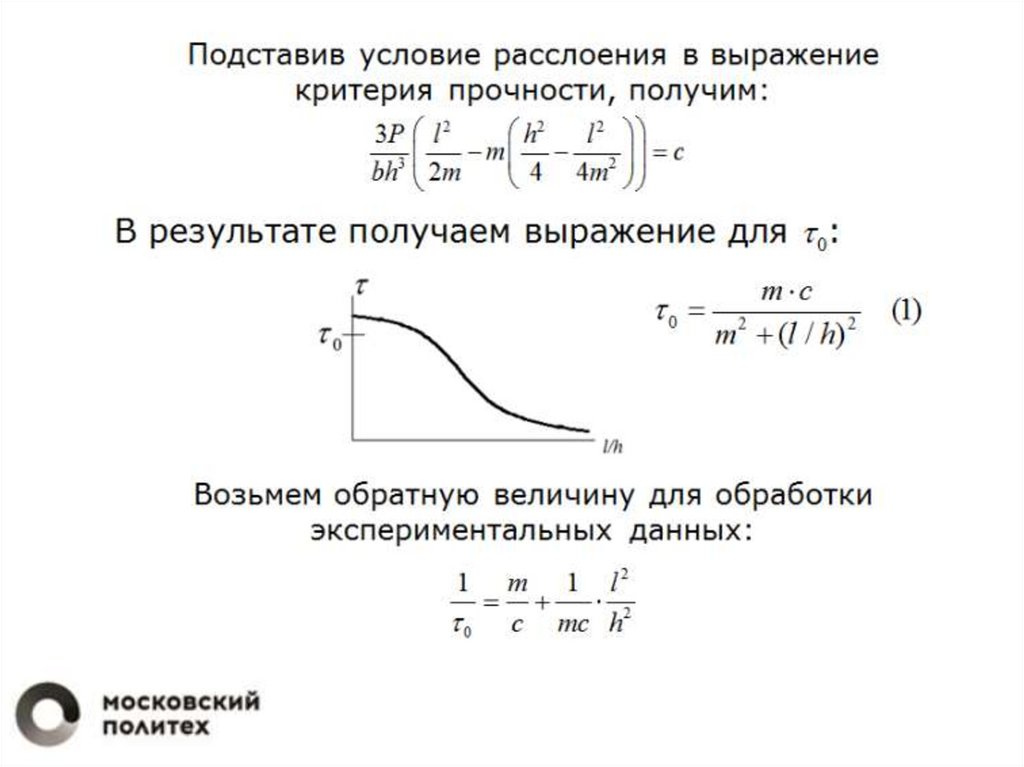
11.

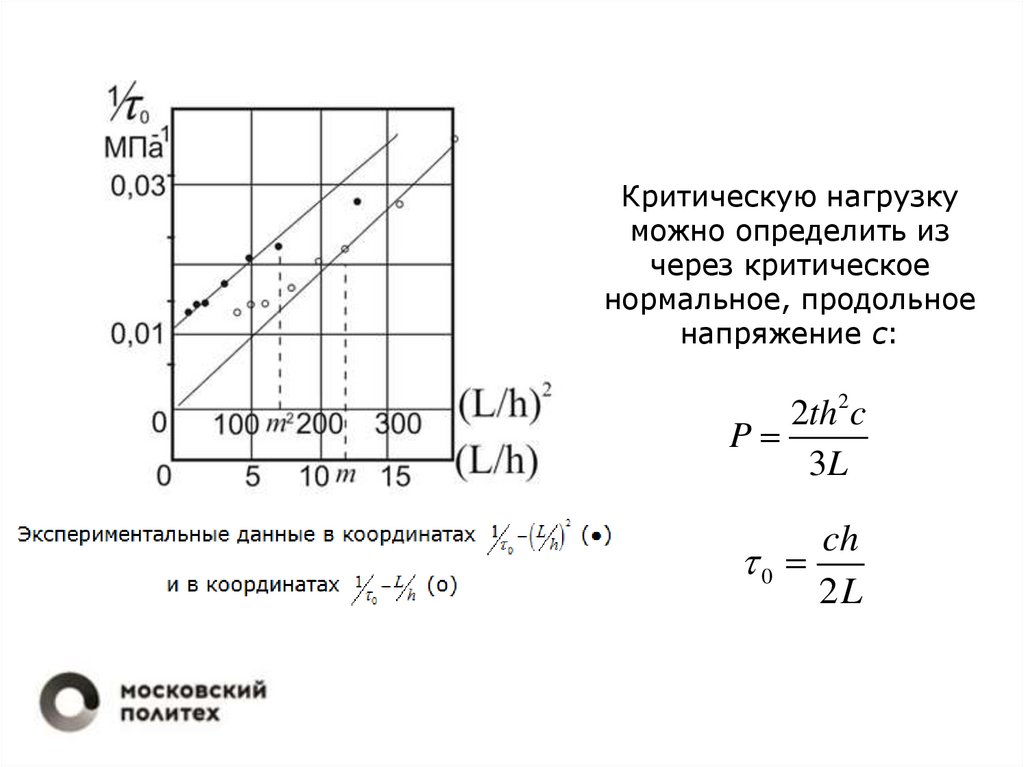
Критическую нагрузку
можно определить из
через критическое
нормальное, продольное
напряжение с:
2th 2c
P
3L
ch
0
2L

12.

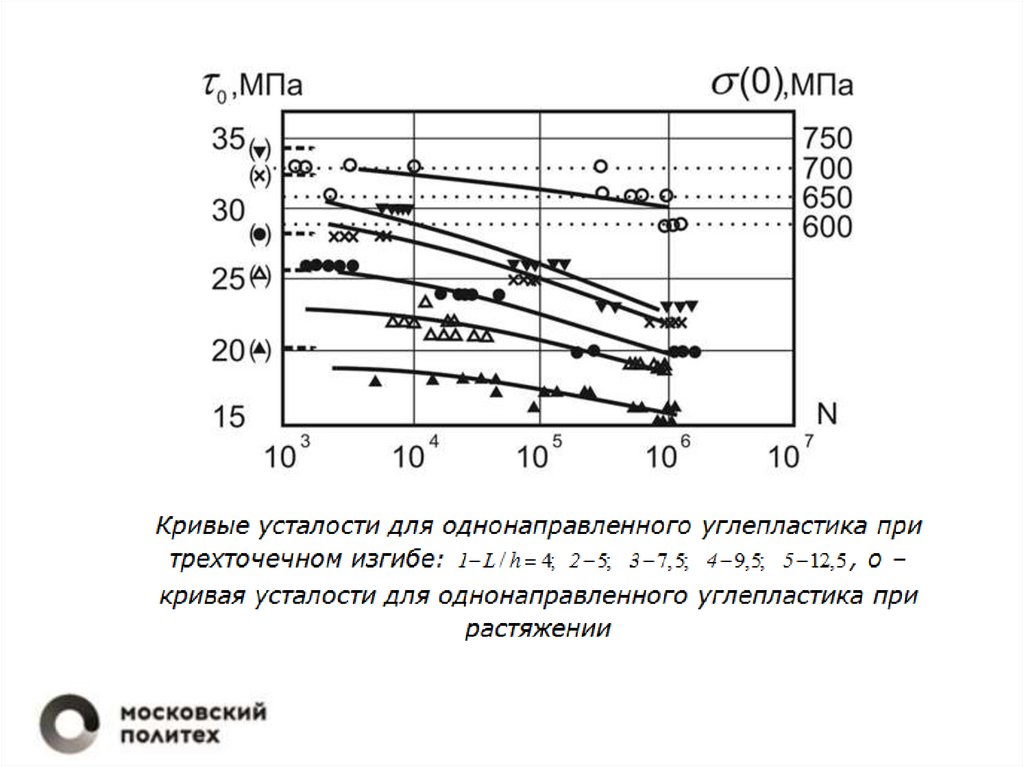
Критерий межслойной прочности при
циклическом изгибе
m N c N m 1 c 1
c N c 1 1 0, 035lg N
0 N , L / h
c 1 m 1
m 1 1 0, 035lg N (L/ h) 2
2
2

13.

14.

Лабораторная работа 8
"Определение параметров
критерия прочности по
результатам испытаний на изгиб
коротких композитных балок".

15.

Исходные данные: h x b = 6 x 6 мм;
Зная зависимость 0
3P
, получим следующие значения:
4 b h
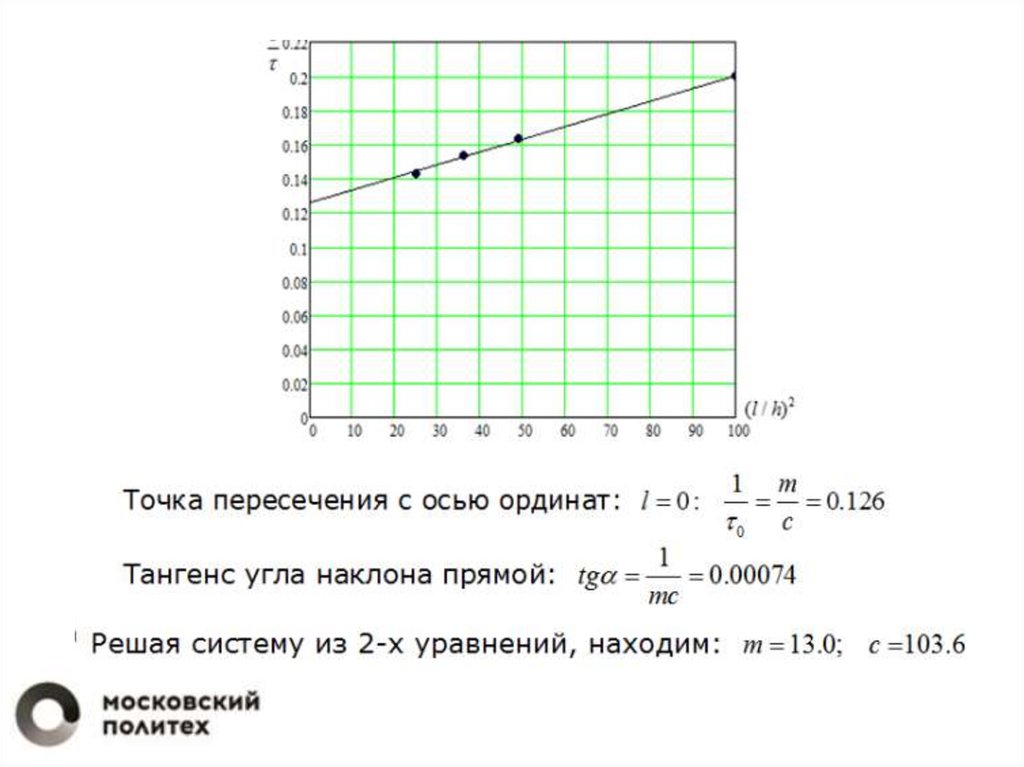
По полученным данным строим методом наименьших квадратов
прямую и проводим её до пересечения с осью ординат.

16.

17.

18.

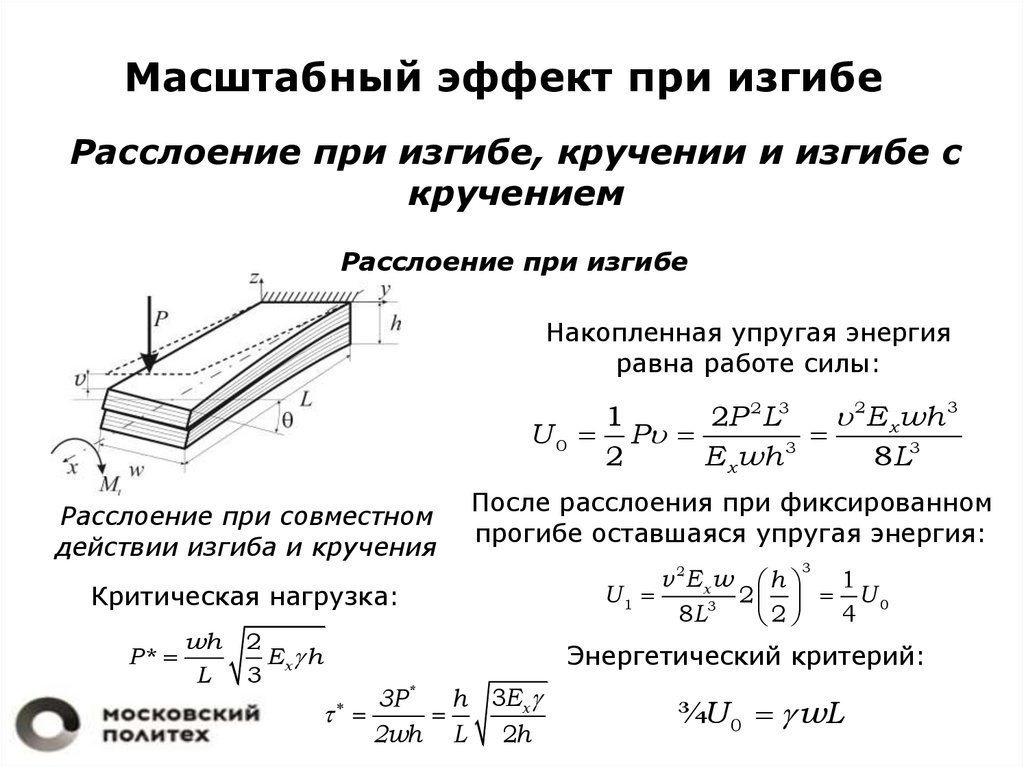
Масштабный эффект при изгибе
Расслоение при изгибе, кручении и изгибе с
кручением
Расслоение при изгибе
Накопленная упругая энергия
равна работе силы:
2E x wh 3
1
2P 2L3
U 0 P
2
E x wh 3
8L3
Расслоение при совместном
действии изгиба и кручения
После расслоения при фиксированном
прогибе оставшаяся упругая энергия:
Критическая нагрузка:
P*
wh
L
2
Ex h
3
3
v 2E x w h
1
U1
2
U0
3
8L
4
2
Энергетический критерий:
3P * h 3E x
2wh L 2h
¾U 0 wL

19.

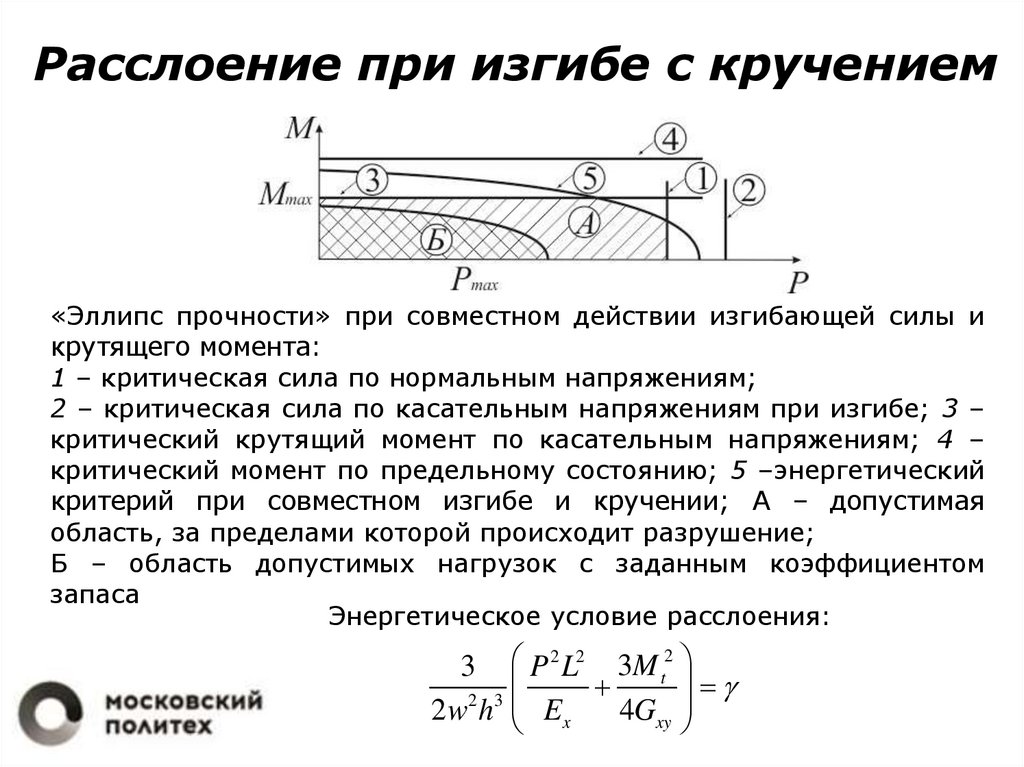
Расслоение при изгибе с кручением
«Эллипс прочности» при совместном действии изгибающей силы и
крутящего момента:
1 – критическая сила по нормальным напряжениям;
2 – критическая сила по касательным напряжениям при изгибе; 3 –
критический крутящий момент по касательным напряжениям; 4 –
критический момент по предельному состоянию; 5 –энергетический
критерий при совместном изгибе и кручении; А – допустимая
область, за пределами которой происходит разрушение;
Б – область допустимых нагрузок с заданным коэффициентом
запаса
Энергетическое условие расслоения:
3 P 2 L2 3M t2
2 3
2w h Ex
4Gxy

20.

Заключение
Предлагаем студентам просмотреть
дополнительные материалы, размещенные в
LMS Политеха (https://lms.mospolytech.ru)

21.

СПАСИБО ЗА ВНИМАНИЕ!