Линейная алгебра просто! интерактивное учебное пособие

1.

ЛИНЕЙНАЯ АЛГЕБРА
ПРОСТО!
ИНТЕРАКТИВНОЕ УЧЕБНОЕ ПОСОБИЕ
Коннова Л.П., Степанян И.К

2.

3.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

4.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

5.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

6.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

7.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

8.

В пособии Вы найдете:
Важные правила, на которые
следует обратить внимание:
1.
2.
3.
4.
5.
6.
7.
8.
Векторы
Линейная зависимость
Действия с матрицами
Метод Гаусса. СЛАУ
Определители
Обратная матрица
Собственные векторы
Квадратичные формы
Схема с основным материалом
темы, которую можно скачать по
значку:
Небольшие тесты, позволяющие
проконтролировать себя:
Вернуться на страницу со
схемой:
Проверь себя
Примеры решения задач:
Некоторые доказательства, интересные и
несложные:
Озвученные примеры:

9.

10.

11.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2

12.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2

13.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2

14.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10
4
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2
4
10
4
10 ( 1)1 3 10 10 5 10 ( 1)1 4 10 10
10
4
2
10
4
10
5
5

15.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10
4
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2
4
10
4
10 ( 1)1 3 10 10 5 10 ( 1)1 4 10 10
10
4
2
10
4
10
5
5

16.

Тема 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Формула Лапласа
2. Вычислите определитель матрицы:
10 10 10 10
10 4 10 4
10 10 5 5
10 4 5 2
Решение:
Попробуем вычислить определитель, используя формулу Лапласа.
Разложим, например, по первой строке.
10 10 10 10
10
4 10
4
10 10
5
5
10
5
2
4
4
1 1
10 ( 1)
10
4
10 4
10 10 4
1 2
10
5
5 10 ( 1)
10
5
5
4
5
2
10
5
2
4
10
4
10 ( 1)1 3 10 10 5 10 ( 1)1 4 10 10
10
4
2
10
4
10
5
5
Вычисление определителя подобным образом достаточно
трудоемкий, хотя и понятный, процесс.

17.

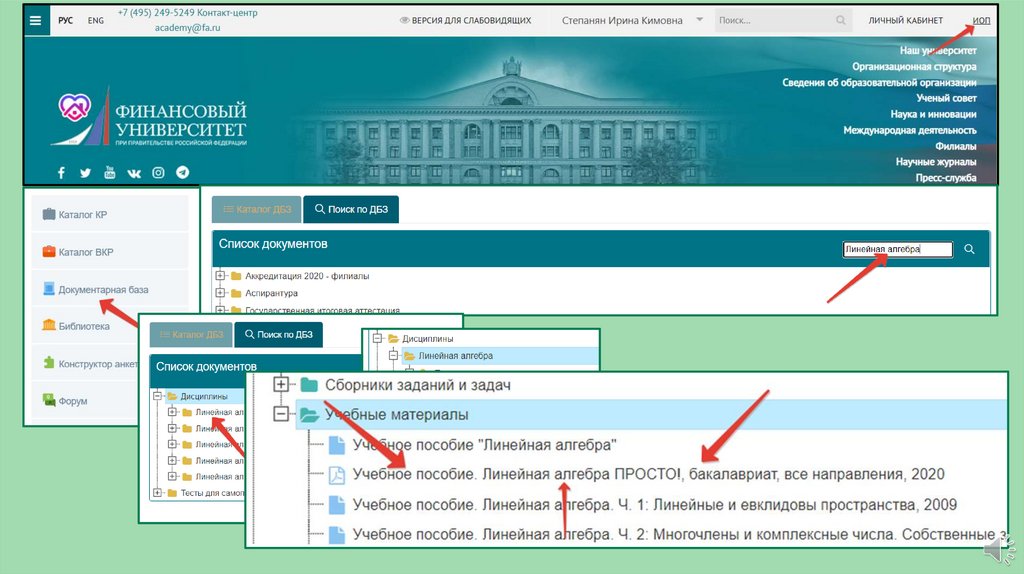
Портал Финуниверситета –Личный кабинет –
Документарная база – Дисциплины –
Учебные материалы – Линейная алгебра –
«Линейная Алгебра ПРОСТО!»
Коннова Л.П., Степанян И.К.