Похожие презентации:
Граничные задачи волноводного распространения
1. Граничные задачи волноводного распространения
1. Поверхностные волны Рэлея (вертикальная поляризация) 1885 гn
y
x
Джон Уильям Сретт (лорд Рэлей)
(1842-1919)
Колебания и волны, оптика, акустика
Рассеяние (голубой цвет неба), закон
Рэлея-Джинса излучения черного тела,
открытие аргона. Нобелевская премия
1904 г.
Особенности формулировки
граничных условий:
1
1) при y 0 Тik nk Тiy n y 0
Т xy y 0 0 Т yy y 0 0
2) при y (виртуальная граница)
упругие смещения отсутствуют
2.
u ul ut2 u l ,t
div ut 0 rotul 0
t 2
Поиск решения в виде
u l ,t U l ,t exp[ i (kx ωt )] f l ,t ( y )
cl2,t 2u l ,t 0
2
2
2 2
x y
2
приводит при подстановке в волновые уравнения к обыкновенному ДУ
для определения функций f :
d 2 f l ,t
dy 2
Проблема выбора решения:
?
2 ω2
k 2 f l ,t 0
cl ,t
k
ω
cl ,t
или
k
ω
cl ,t
Волны бегущие не только вдоль границы: решение для них неопределенно
из-за невозможности формулирования ГУ на виртуальной границе y
3.
Условиеω
k
cl ,t
означает:
1) Медленность распространения
ω
ω
ω
волны Рэлея (только вдоль границы!) k
v R cl ,t
vR
v R cl ,t
по сравнению с обеими
типами волн L и T в безграничной
среде
2) Возможность представления функций f l,t в виде
ω2
f l ,t exp( α l ,t y ) α l ,t k 2
cl ,t
2
Теперь отбор решения в области y<0 можно осуществить,
руководствуясь требованием ограниченности (|u|<M отбору
положительного корня), не вступая в противоречие с удовлетворением
ГУ на виртуальной границе: |u| 0 при y
4.
u [U l exp( α l y ) U t exp( α t y )]e i ( kx ωt )Решение образовано суперпозицией продольной и поперечной
неоднородных волн
Общее решение требует конкретизации:
1) Установление связи между вектор-амплитудами Ul и Ut
с возможностью выделения общего амплитудного
коэффициента
2) Установление связи между k и т.е. закона дисперсии
волны Рэлея
5.
Вектор-амплитуды: 4 неизвестных U lx , U ly , U tx , U tyСвязи между ними устанавливают 2 граничных условия
Т xy y 0 0
и 2 уравнения
Т yy y 0 0
div ut 0 rotul 0
Задача замкнута.
Общая формула для компонент тензора напряжений
Т ik 2ρct2uik ρ(cl2 2ct2 )ull δik
6.
Т xy ρct2u x
ρct2iku y
y
Т yy (cl2 2ct2 )ikux
cl2
u y
y
uty
k
utx uty
i
(I)
div ut 0
0 ikutx αt uty 0
x
y
utx
αt
rotu l 0
i
x
ulx
j
y
uly
k
uly u
0 k
lx 0
y
x
0
ikuly α l ulx 0
ulx ik
uly α l
(II)
7.
С учетом (I), (II)Т xy y 0 0 Т yy y 0 0
дают
αt 2ikuly (k 2 αt2 )utx 0
α l2 k 2 (1 2ct2 / cl2 )
ct2
uly
2ik 2 utx 0
αl
cl
Система однородных алгебраических уравнений относительно
составляющих векторов смещений u и u ly что равносильно
tx
уравнениям относительно составляющих вектор-амплитуд.
Условие разрешимости системы Det=0 дает дисперсионное соотношение
волны Рэлея
(k 2 α t2 ) 4k 2 α l α t
Из самих уравнений и уравнений (I), (II) можно установить общий
амплитудный коэффициент для неоднородных волн L и T-типа
8.
Подстановкаω2
α l ,t k 2
cl ,t
2
в дисперсионное соотношение
дает искомую связь k( )
2 ω
2k 2
ct
2
С заменой
Так как
Рэлея
4
ω 2 2 ω 2
4 2
16k k 2 k 2
ct
cl
ω сt kξ
для получаем бикубическое уравнение
2
2
с
с
6
4
2
t
t
ξ 8ξ 8ξ 3 2 2 16 1 2 0
cl
cl
сt
1 2ν
величина и фазовая скорость волны
cl 2(1 ν )
v R ξct
зависят только от коэффициента Пуассона
9.
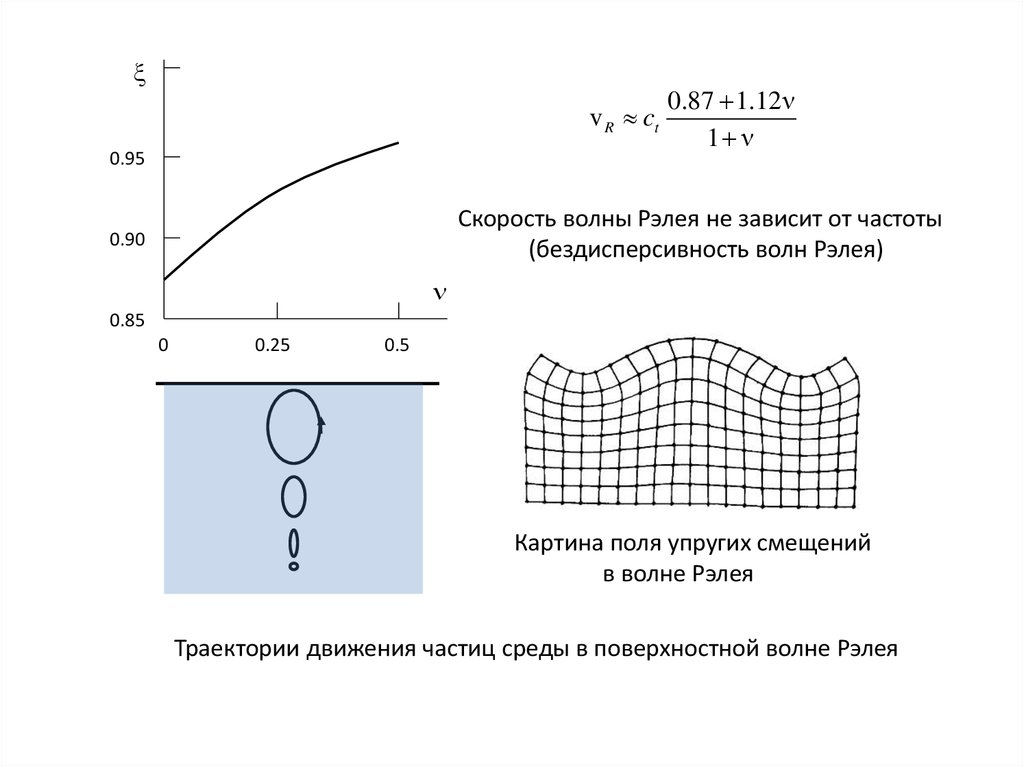
v R ct0.95
0.87 1.12 ν
1 ν
Скорость волны Рэлея не зависит от частоты
(бездисперсивность волн Рэлея)
0.90
0.85
0
0.25
0.5
Картина поля упругих смещений
в волне Рэлея
Траектории движения частиц среды в поверхностной волне Рэлея
10.
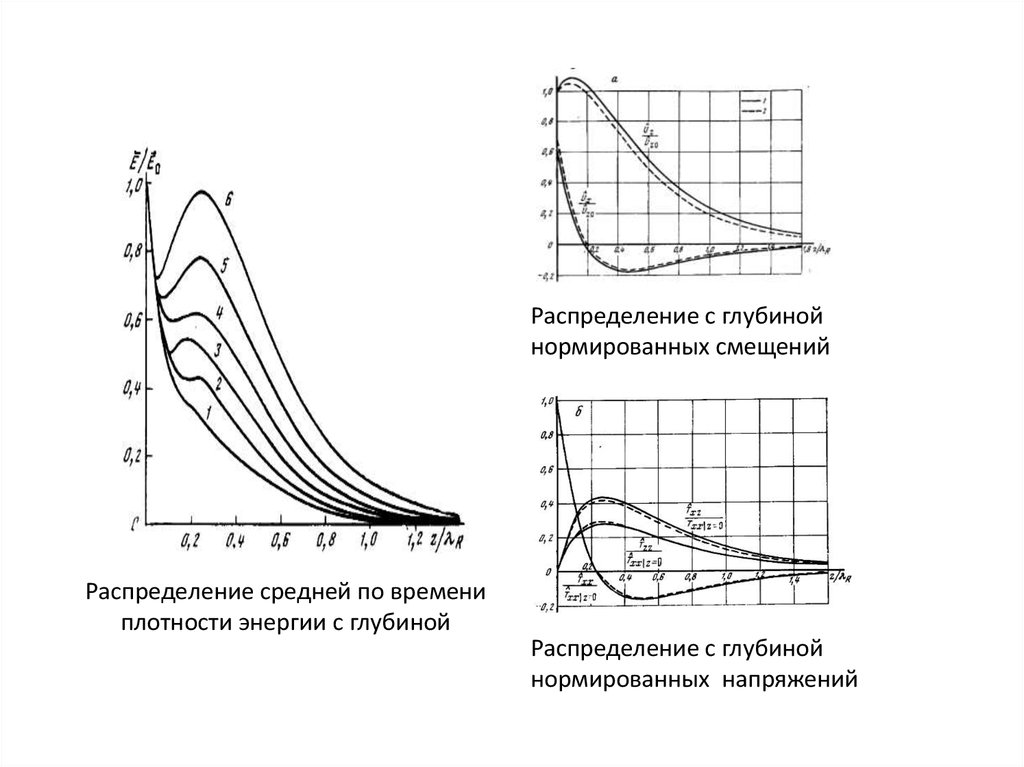
Распределение с глубинойнормированных смещений
Распределение средней по времени
плотности энергии с глубиной
Распределение с глубиной
нормированных напряжений
11.
Кварцевая пластинка Х-срезаМетод клина, преобразующего
падающую под специальным углом
продольную волну в волну Рэлея
Кварцевая пластинка Y-среза
с жидкой связкой
Гребенчатая структура
12.
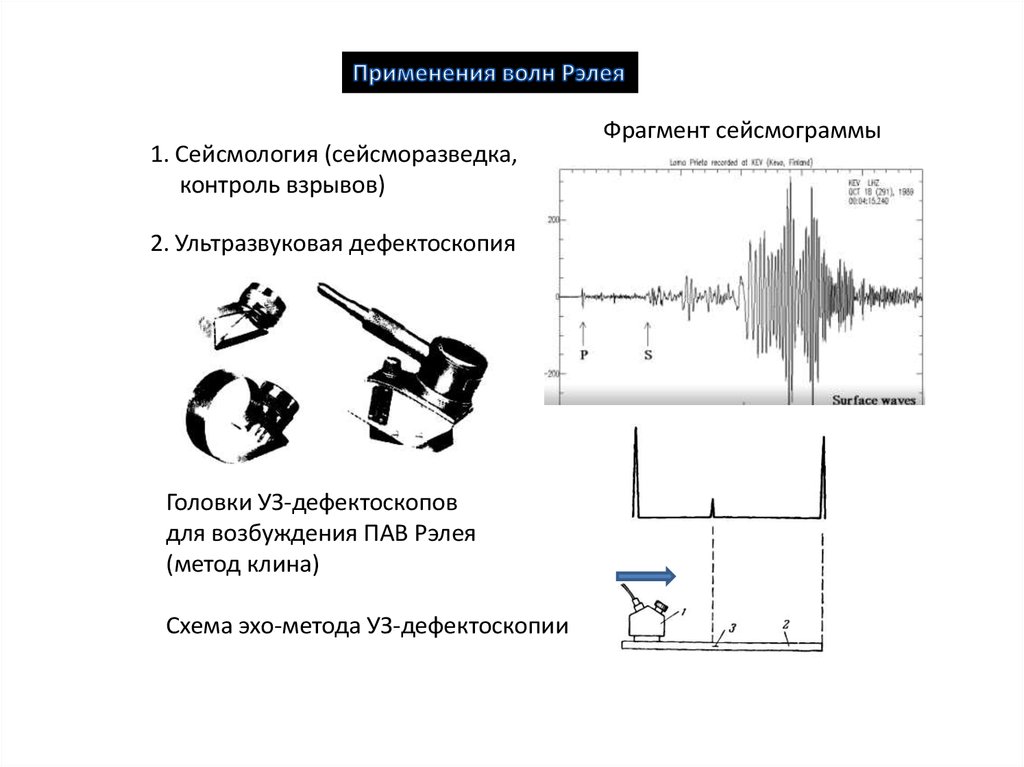
1. Сейсмология (сейсморазведка,контроль взрывов)
2. Ультразвуковая дефектоскопия
Головки УЗ-дефектоскопов
для возбуждения ПАВ Рэлея
(метод клина)
Схема эхо-метода УЗ-дефектоскопии
Фрагмент сейсмограммы
13.
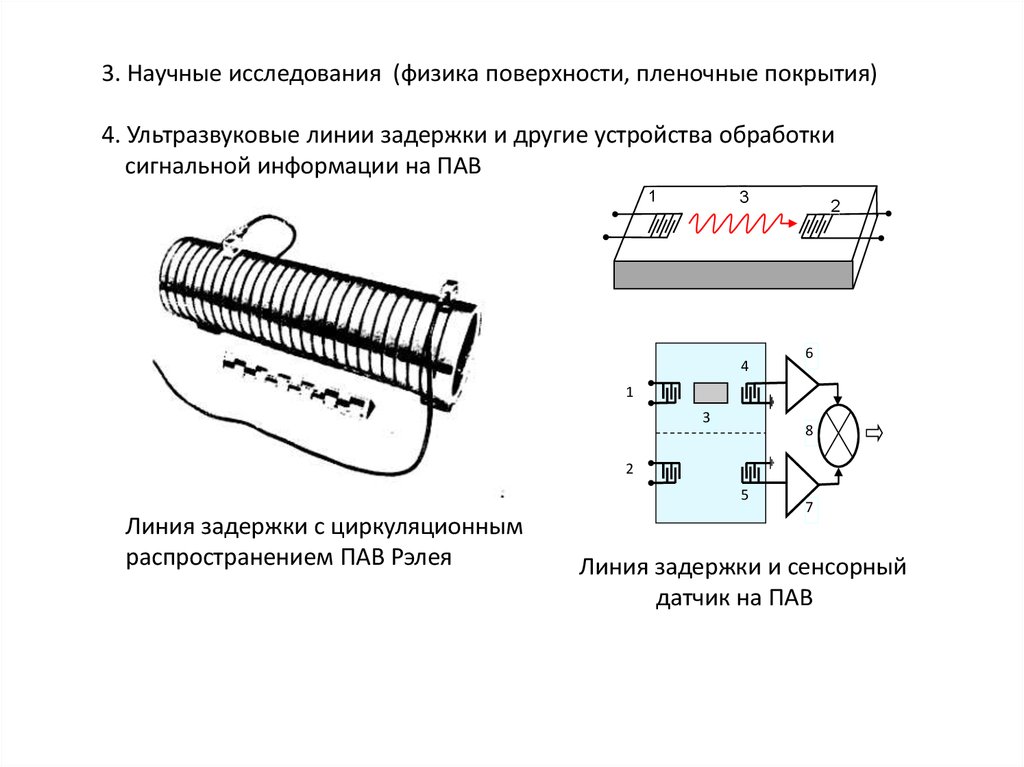
3. Научные исследования (физика поверхности, пленочные покрытия)4. Ультразвуковые линии задержки и другие устройства обработки
сигнальной информации на ПАВ
1
3
4
2
6
1
3
8
2
5
Линия задержки с циркуляционным
распространением ПАВ Рэлея
7
Линия задержки и сенсорный
датчик на ПАВ
14.
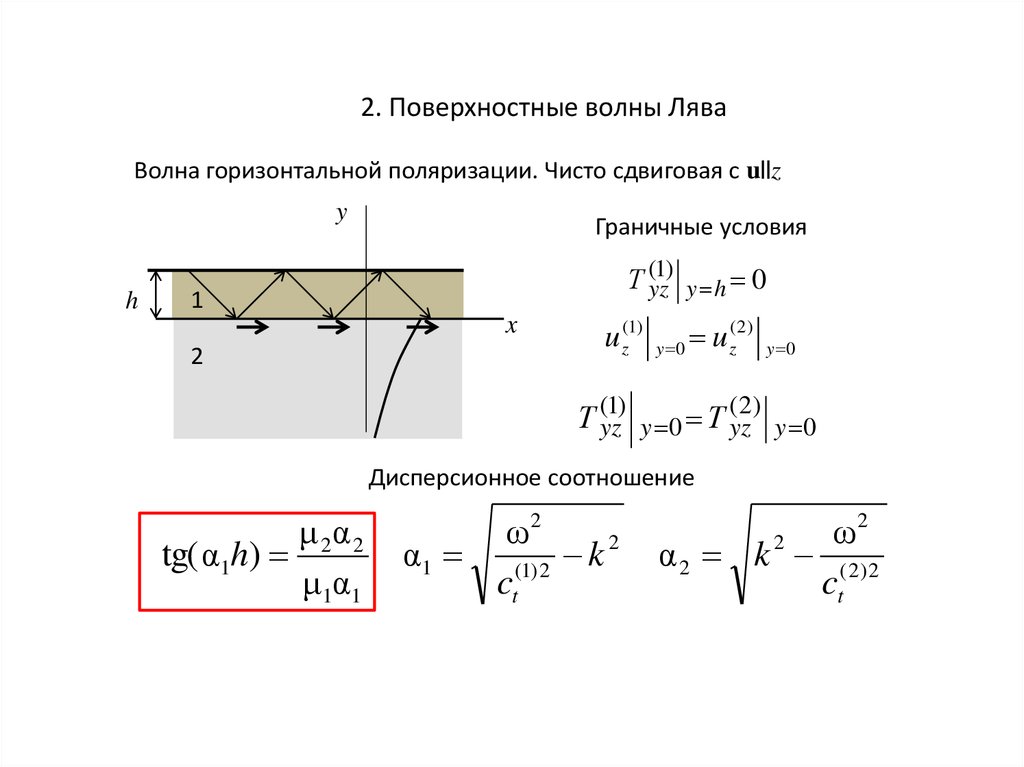
2. Поверхностные волны ЛяваВолна горизонтальной поляризации. Чисто сдвиговая с u||z
y
h
Граничные условия
Т (yz1) y h 0
1
x
2
u z(1)
( 2)
u
y 0
z
y 0
Т (yz1) y 0 Т (yz2) y 0
Дисперсионное соотношение
μ 2α 2
tg(α1h)
μ1α1
ω2
α1 (1) 2 k 2
ct
2
ω
α 2 k 2 ( 2) 2
ct
15.
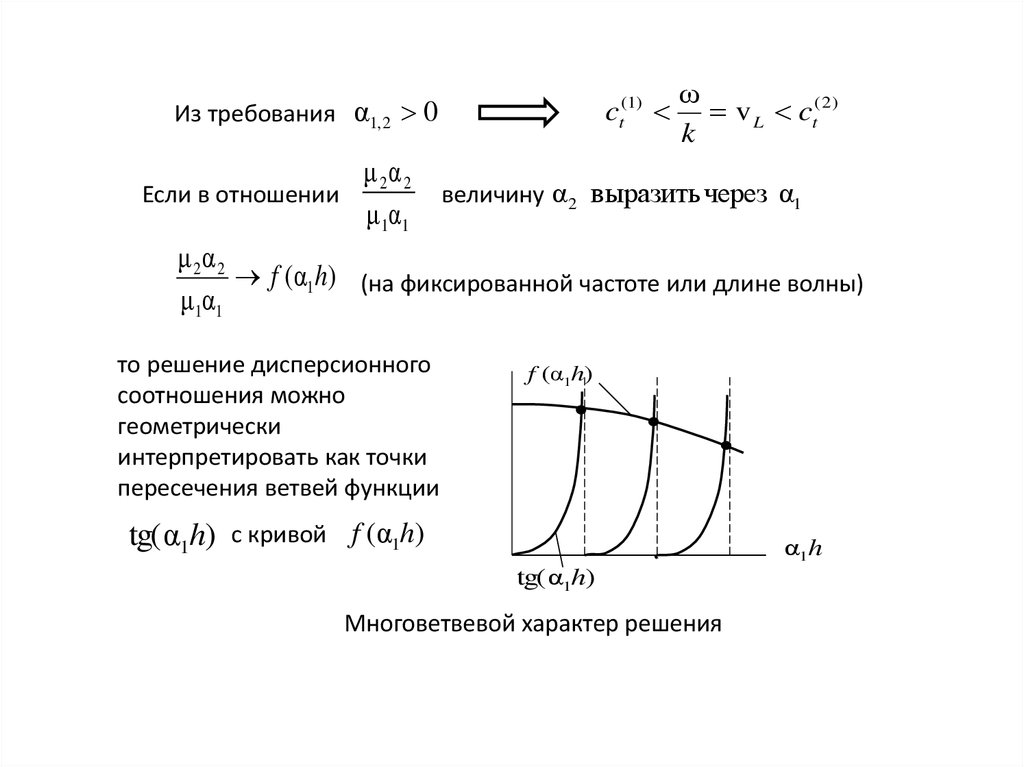
Из требования α1, 2 0Если в отношении
μ 2α 2
μ1α1
ct(1)
ω
v L ct( 2 )
k
величину α2 выразить через α1
μ 2α 2
f (α1h) (на фиксированной частоте или длине волны)
μ1α1
то решение дисперсионного
соотношения можно
геометрически
интерпретировать как точки
пересечения ветвей функции
f (α1h)
tg(α1h) с кривой f (α1h)
α1h
tg(α1h)
Многоветвевой характер решения
16.
ω kct( 2 )3
2
h
ω kc
1
3
2
1
(1)
t
1
1
k
Спектр мод Лява с
выраженной частотной
дисперсией
Распределение сдвиговых смещений
по глубине в модах волн Лява










 Физика
Физика








