Похожие презентации:
Топологические модели электронных схем. Полюсные графы, топологические матрицы и топологические уравнения
1.
Дисциплина «Методы анализа ирасчета электронных схем»
ТЕМА: «Топологические модели электронных схем
(полюсные графы, топологические матрицы
и топологические уравнения)»
Легостаев Николай Степанович,
доцент кафедры «Промышленная электроника»
2.
Полюсные графыГраф G(X, A, Γ) представляет собой совокупность непустого множества
вершин X (X ≠ ∅), не пересекающегося с ним множества ребер A (A ∩ X = ∅) и
закона Z, устанавливающего взаимосвязь между элементами множества вершин с
помощью элементов множества ребер.
Аналитически закон Z описывается логическим высказыванием следующего вида:
ì1, åñëè xi , x j ñâÿçàí û ðåáðî ì ak ;
ï
Z ( xi , ak , x j ) = í
ï0, åñëè xi , x j í å ñâÿçàí û ðåáðî ì ak ,
î
которое означает, что ребро
Вершины
xi
и
ak
соединяет вершины
xi
и
x j.
x j называются смежными, а ребро ak
(принадлежащим), этим вершинам.
– инцидентным
3.
Полюсные графыПолюсный граф электронной схемы представляет собой граф, вершины
которого соответствуют узлам схемы, ребра — ветвям схемы, а в качестве
закона Z выступает порядок связей ветвей схемы между собой. Ребрам полюсного
графа приписывают направления, совпадающие с положительными направлениями
токов соответствующих ветвей. При этом в ветви, содержащей источник ЭДС,
положительное направление тока следует выбирать противоположным
направлению ЭДС. Последовательно и параллельно включенные ветви схемы в
полюсном графе могут быть объединены в эквивалентные дуги.
В зависимости от вида компонентных уравнений ребра разбивают на два
подмножества: y-ребра (компонентные уравнения выражают токи) и z-ребра
(компонентные уравнения выражают напряжения). Ребра, компонентные
уравнения которых записываются как для токов, так и для напряжений, называют
взаимно определенными.
4.
Полюсные графыКомпонент
электронной схемы
Вид компонентного
уравнения
Тип ребра
u
i = , u = r ×i
r
du
ic = C c
dt
di
uL = L L
dt
взаимно
определенное
y - ðåáðî
z - ðåáðî
E = const
z - ðåáðî
J = const
y - ðåáðî
Графическое
представление в
графе
5.
Полюсные графыПорядок составления полюсного графа для электронной схемы:
● составляется схема замещения по переменному току, в которой
электронные компоненты представляют соответствующими
условными графическими обозначениями (УГО);
● в схеме замещения по переменному току активные электронные
компоненты замещают соответствующими эквивалентными схемами,
содержащими только двухполюсные компоненты;
● вершины графа ставят в соответствии узлам схемы;
● ребра графа ставят в соответствии ветвям схемы;
● вершины и ребра графа нумеруют, например, арабскими
(или римскими) цифрами;
● ребрам полюсного графа приписывают направление.
6.
Полюсные графыОсновные термины и определения
Совокупность ребер, соединенных с некоторой вершиной, называют ребрами,
инцидентной данной вершине.
Путь – последовательность вершин и ребер, в которой двум вершинам
(начальной и конечной) инцидентны по одному ребру, а остальным вершинам
(внутренним) инцидентны по два ребра.
Путь, который начинается и заканчивается в одной и той же вершине и не проходит
дважды через другие вершины, является замкнутым путем (контуром).
Контур, состоящий из одного ребра, называется петлей.
Связный граф – граф, в котором между любыми двумя вершинами можно найти путь.
Любая связная совокупность ребер графа, не содержащая контуров, вместе с
инцидентными им вершинами образуют дерево графа. Если такое дерево является
суграфом, то оно называется покрывающим деревом или остовом.
Часть графа, содержащая некоторое подмножество ребер и все вершины исходного графа,
называется суграфом.
7.
Полюсные графыОсновные термины и определения
Дерево на множестве вершин u всегда содержит n
= (u - 1) ребер, то есть
минимальное количество ребер, необходимое для того, чтобы граф был связным.
Ребра, не вошедшие в дерево, составляют дополнение этого дерева и называются
хордами (главными ветвями).
Сечением называют замкнутую линию, пересекающую некоторое количество ребер,
устранение которых делает граф несвязным, при этом каждое ребро должно
пересекаться нечетное количество раз (чаще всего один раз).
Сечение, пересекающее только одну ветвь дерева, называется главным сечением.
Главный контур включает только одну хорду, направление которой принимают
за направление контура.
8.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
● составляется схема замещения по переменному току, в которой
электронные компоненты представляют соответствующими условными
графическими обозначениями (УГО)
Рис. 2.1 – Электронная схема
Рис. 2.2 – Схема замещения электронной
схемы рис.2.1 по переменному току для
полного диапазона частот
9.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
● в схеме замещения по переменному току активные электронные компоненты
замещают соответствующими эквивалентными схемами, содержащими только
двухполюсные компоненты
З – затвор полевого транзистора.
С – сток полевого транзистора.
и – исток полевого транзистора.
Uзи – напряжение затвор-исток
полевого транзистора.
SUзи –
Рис. 2.3 – Схема замещения
полевого транзистора
зависимый источник тока,
управляемый напряжением.
10.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
Рис. 2.4 – Схема замещения электронной схемы рис.2.1 по переменному
току для полного диапазона частот, в которой полевой транзистор
представлен эквивалентной схемой замещения.
11.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
● вершины графа ставят в соответствии
узлам схемы;
● ребра графа ставят в соответствии
ветвям схемы;
● вершины и ребра графа нумеруют,
например, арабскими (или римскими)
цифрами.
Рис. 2.5 – Топологический граф электронной схемы рис. 2.1, составленный по
схеме рис. 2.4
12.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
При формировании уравнений все взаимно
Рис. 2.6 – Граф взаимно
определенных ребер
определенные ребра должны быть отнесены
либо к z-ребрам, либо к y-ребрам.
С целью оптимального разбиения взаимно
определенных
ребер,
обеспечивающего
образование
максимального
количества
вырожденных координат получают граф взаимно
определенных ребер путем закорачивания всех yребер и размыкания всех z-ребер.
К y-ребрам следует отнести те взаимно определенные ребра, которые в графе взаимно
определенных ребер (рис.2.6) оказываются включенными параллельно, либо образуют
петли . Все остальные взаимно определенные ребра относят к z-ребрам.
Из графа рис. 2.6 следует, что все взаимно определенные ребра необходимо отнести
к y-ребрам.
13.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
● ребрам полюсного графа
приписывают направление;
Рис. 2.7 – Полюсный граф электронной схемы рис. 2.1
14.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
Ребра дерева (ребра 2,4,5,9,11 и 12)
называют ветвями
– ветви дерева
Рис. 2.8 – Дерево для полюсного графа электронной схемы рис. 2.1
15.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
Количество вырожденных сечений
определяется выражением
n
n ¢ = n y - n,
где
– количество частей исходного
графа; y – количество частей графа,
полученного из исходного путем
n
размыкания всех z-ребер.
Для графа рис. 2.9 : n
= 1; n y = 1; n ¢ = 0
Рис. 2.9 – Система главных сечений (вырожденных сечений нет)
16.
Полюсные графыПример составления полюсного графа для электронной схемы рис.2.1.
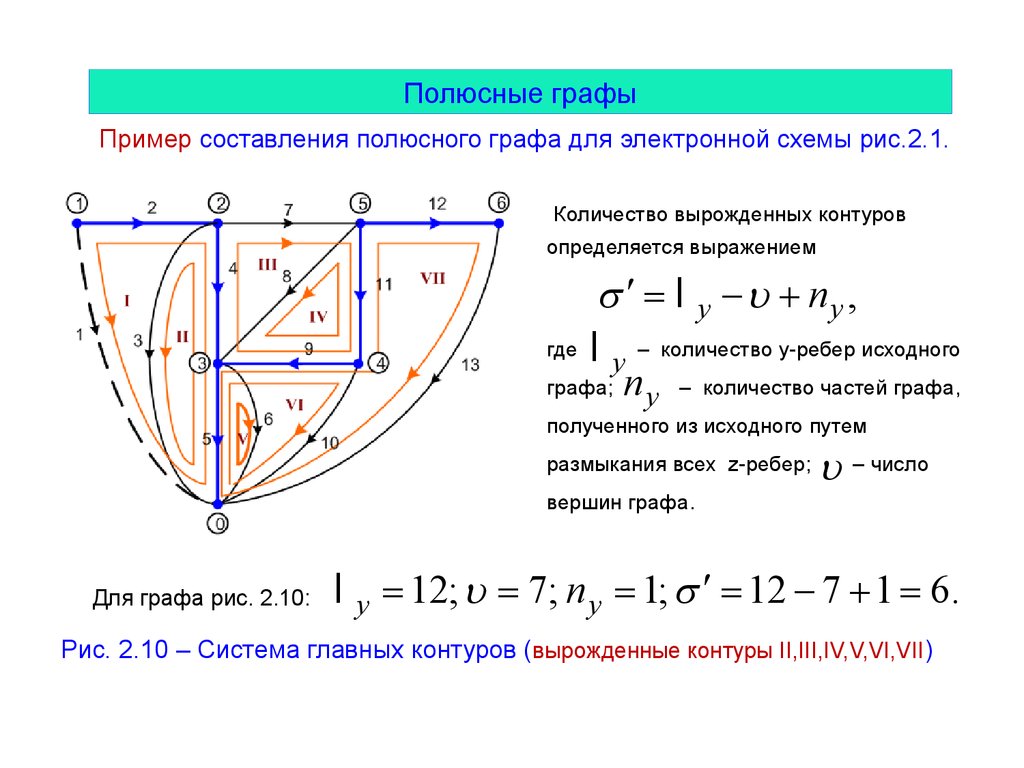
Количество вырожденных контуров
определяется выражением
s ¢ = l y - u + ny ,
где l
– количество y-ребер исходного
y
графа; n
y – количество частей графа,
полученного из исходного путем
размыкания всех z-ребер;
u – число
вершин графа.
Для графа рис. 2.10:
l y = 12; u = 7; n y = 1; s ¢ = 12 - 7 + 1 = 6.
Рис. 2.10 – Система главных контуров (вырожденные контуры II,III,IV,V,VI,VII)
17.
Полюсные графыСечение, которому инцидентны
только z-ребра, является вырожденным.
Контур (цикл), которому инцидентны
только y-ребра, является вырожденным.
18.
Полюсные графыЗадание 1: Определите число вырожденных циклов полюсного графа.
s ¢ = l y - u + ny ,
Контур (цикл), которому инцидентны только y-ребра, является вырожденным.
19.
Полюсные графыКоличество вырожденных контуров
определяется выражением
s ¢ = l y - u + ny ,
где l
– количество y-ребер исходного графа; n
y
y
– количество частей графа,
полученного из исходного путем размыкания всех z-ребер;
l y = 5; u = 5; n y = 2; s ¢ = 5 - 5 + 2 = 2.
Правильный ответ на задание 1:
2
u
– число вершин графа.
20.
Полюсные графыЗадание 2: Определите число вырожденных сечений полюсного графа.
n ¢ = ny - n
Сечение, которому инцидентны только z-ребра, является вырожденным.
21.
Полюсные графыn ¢ = n y - n = 2 - 1 = 1.
Количество вырожденных сечений определяется выражением
n ¢ = n y - n,
где n – количество частей исходного графа; n y – количество частей графа,
полученного из исходного путем размыкания всех z-ребер.
Правильный ответ на задание 2:
1
22.
Полюсные графыЗадание 3: Для приведенного варианта выбора главного дерева
графа укажите номер неправильно выбранного главного контура.
23.
Полюсные графыРешение задания 3:
Правило: главному контуру инцидентна одна хорда.
Анализ: Контуру I инцидентна одна хорда (это хорда 1),
контуру II инцидентна одна хорда (это хорда 4),
контуру IV также инцидентна одна хорда (это хорда 8),
а контуру III инцидентны две хорды (хорды 4 и 5).
Правильный ответ на задание 3: контур III – неправильно выбранный контур
24.
Полюсные графыЗадание 4: Для приведенного варианта выбора главного дерева
графа укажите номер неправильно выбранного главного сечения.
25.
Полюсные графыРешение задания 4 :
Правило: главному сечению инцидентна одна ветвь дерева.
Анализ: Сечению I инцидентна одна ветвь (это ветвь 2),
сечению III инцидентна одна ветвь (это ветвь 7),
сечению IV также инцидентна одна ветвь (это ветвь 6),
а сечению II инцидентны две ветви (ветви 2 и 3).
Правильный ответ на задание 4: сечение II – неправильно выбранное сечение.
26.
Полюсные графыЗадание 5: Для приведенного варианта выбора главного дерева
графа укажите номера вырожденных контуров.
27.
Полюсные графыРешение задания 5: Для приведенного варианта выбора главного
дерева графа укажите номера вырожденных контуров.
Правильный ответ на задание 5: вырожденными являются контуры II и III.
28.
Топологические матрицыРис. 2.11 – Схема эмиттерного
повторителя
Рис. 2.12 – Схема замещения эмиттерного
повторителя (рис.2.11) по переменному току
для полного диапазона частот
29.
Топологические матрицыR1 × R2
´
R1 + R2
Zý =
R1 × R2
+
R1 + R2
Рис. 2.13 – Схема замещения эмиттерного
повторителя (рис.2.11) по переменному току
для полного диапазона частот
1
pC1
;
1
pC1
30.
Топологические матрицыРис. 2.14 – Эквивалентная
схема биполярного транзистора
(низкочастотная)
Рис. 2.15 – Схема замещения эмиттерного
повторителя (рис. 2.11) по переменному току,
в которой биполярный транзистор представлен
эквивалентной низкочастотной схемой (рис. 2.14).
31.
Топологические матрицыДля удобства формирования топологических матриц составляется
топологический граф.
Рис. 2.16 – Топологический граф, соответствующий схеме замещения рис. 2.15.
32.
Топологические матрицыЭлементы матрицы невырожденных контуров (матрица Т )
определяются условным выражением:
ì1, j - ÿ âåò âü í àï ðàâëåí à ñî ãëàñí î ñ i - ì êî í ò óðî ì
ï
rij¢ = í-1, j - ÿ âåò âü í àï ðàâëåí à ï ðî ò èâî ï î ëî æ í î i - ì ó êî í ò óðó
ï0, j - ÿ âåò âü í å èí öèäåí ò í à i - ì ó êî í ò óðó
î
Элементы матрицы невырожденных сечений (матрица
определяются условным выражением:
Ï ¢)
ì1, j - ÿ âåò âü í àï ðàâëåí à ñî ãëàñí î ñ i - ì ñå÷åí èåì
ï
p ij¢ = í-1, j - ÿ âåò âü í àï ðàâëåí à ï ðî ò èâî ï î ëî æ í î i - ì ó ñå÷åí èþ
ï0, j - ÿ âåò âü í å èí öèäåí ò í à i - ì ó ñå÷åí èþ
î
33.
Топологические матрицыРис. 2.17 – Система главных контуров
( вырожденный контур III )
¢
Ð=
1
2
3
4
5
6
7
8
9
10
I
+1
–1
–1
0
0
0
0
0
0
0
II
0
0
–1
+1
+1
+1
0
0
0
0
IV
0
0
0
0
0
0
0
–1
–1
+1
Рис. 2.18 – Топологическая матрица главных невырожденных контуров
(составлена с использованием графа рис.2.17 ).
34.
Топологические матрицыДля формирования системы уравнений из матрицы главных контуров
необходимо выделить:
подматрицу главных невырожденных контуров для y-ветвей (подматрица Т )
y
и
подматрицу главных невырожденных контуров для z-ветвей (подматрицаТ ).
z
Тy =
Тz =
2
5
6
7
8
9
I
–1
0
0
0
0
0
II
0
+1
+1
0
0
0
IV
0
0
0
0
–1
–1
1
3
4
10
I
+1
–1
0
0
II
0
–1
+1
0
IV
0
0
0
+1
35.
Топологические матрицыРис. 2.19 – Система главных сечений
( вырожденное сечение 2 )
Ï ¢=
1
2
3
4
5
6
7
8
9
10
1
+1
+1
0
0
0
0
0
0
0
0
3
0
0
0
–1
+1
0
–1
0
0
0
4
0
0
0
–1
0
+1
–1
0
0
0
5
0
0
0
0
0
0
+1
+1
0
+1
6
0
0
0
0
0
0
0
0
+1
+1
Рис. 2.20 – Топологическая
матрица главных
невырожденных сечений
(составлена
с использованием графа
рис.2.19 ).
36.
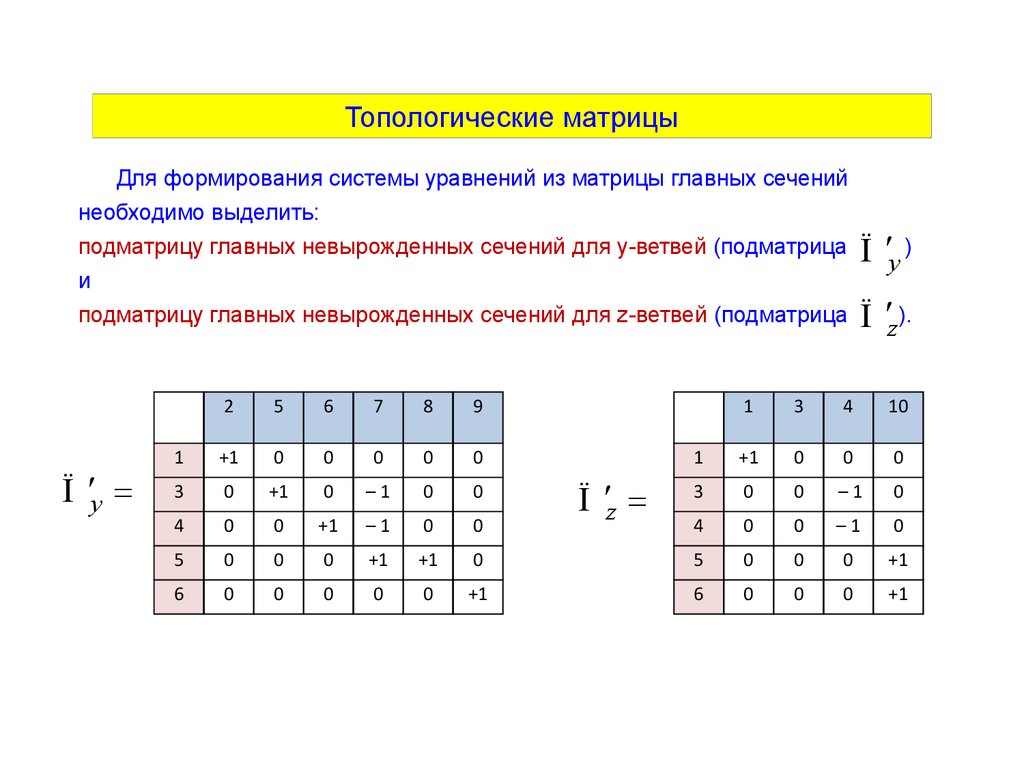
Топологические матрицыДля формирования системы уравнений из матрицы главных сечений
необходимо выделить:
подматрицу главных невырожденных сечений для y-ветвей (подматрица
и
подматрицу главных невырожденных сечений для z-ветвей (подматрица
Ï ¢y =
2
5
6
7
8
9
1
+1
0
0
0
0
0
3
0
+1
0
–1
0
0
4
0
0
+1
–1
0
0
5
0
0
0
+1
+1
6
0
0
0
0
0
Ï ¢y )
Ï ¢z).
1
3
4
10
1
+1
0
0
0
3
0
0
–1
0
4
0
0
–1
0
0
5
0
0
0
+1
+1
6
0
0
0
+1
Ï ¢z =
37.
Топологические матрицыМатрица Yâ проводимостей y-ветвей представляет
собой квадратную матрицу, порядок которой равен
числу y-ветвей.
Yâ =
2
5
6
7
8
9
2
pC2
0
0
0
0
5
0
1
rá
0
0
0
0
0
6
0
0
1
Rý ( p )
0
0
0
7
0
0
0
1
rê
0
0
8
0
0
0
0
1
R3
0
9
0
0
0
0
0
pC3
38.
Топологические матрицыМатрица Z â сопротивлений z-ветвей представляет
собой квадратную матрицу, порядок которой равен
числу z-ветвей.
Zâ =
1
3
4
10
1
rc
0
0
0
3
0
R4
0
0
4
0
0
10
0
0
rý
0
0
Rí
39.
Топологические матрицыМатрица N зависимых источников тока,
управляемых током, имеет размерность
(l y ´ l z ) .
N=
1
3
4
10
2
0
0
0
0
5
0
0
0
0
6
0
0
0
0
7
0
0
8
0
0
0
0
9
0
0
0
0
a
0
40.
Топологические матрицыМатрица M зависимых источников
напряжения, управляемых напряжением,
имеет размерность
(l z ´ l y ) .
M=
2
5
6
7
8
9
1
0
0
0
0
0
0
3
0
0
0
0
0
0
4
0
0
0
0
0
0
10
0
0
0
0
0
0
41.
Топологические матрицыКоличество элементов вектора J â задающих
токов определяется числом y-ветвей, причем
его элементами выступают токи независимых
источников тока.
Количество элементов вектора E задающих
â
ЭДС определяется числом z-ветвей, причем
его элементами выступают ЭДС независимых
источников напряжения.
Jâ =
2
0
5
0
6
0
7
0
8
0
9
0
Eâ =
1
ec
3
0
4
0
10
0
42.
Топологические матрицыЗадание 6: Для приведенного варианта выбора покрывающего дерева
графа укажите значение элемента матрицы главных сечений,
отмеченного символом «х».
Ï=
1
2
3
4
5
6
7
8
1
1
1
0
0
0
0
0
0
3
0
–1
1
х
0
–1
0
1
5
0
0
0
0
1
1
0
–1
7
0
0
0
–1
0
1
1
0
43.
Топологические матрицыРешение задание 6: Для приведенного варианта выбора
покрывающего дерева графа укажите значение элемента матрицы
главных сечений, отмеченного символом «х».
ì1, j - ÿ âåò âü í àï ðàâëåí à ñî ãëàñí î ñ i - ì ñå÷åí èåì
ï
p ij = í-1, j - ÿ âåò âü í àï ðàâëåí à ï ðî ò èâî ï î ëî æ í î i - ì ó ñå÷åí èþ
ï0, j - ÿ âåò âü í å èí öèäåí ò í à i - ì ó ñå÷åí èþ
î
Ï=
1
2
3
4
5
6
7
8
1
1
1
0
0
0
0
0
0
3
0
–1
1
1
0
–1
0
1
5
0
0
0
0
1
1
0
–1
7
0
0
0
–1
0
1
1
0
Правильный ответ на задание 6: 1 – значение элемента
44.
Топологические матрицыЗадание 7: Для приведенного варианта выбора покрывающего дерева
графа укажите значение элемента матрицы главных контуров,
отмеченного символом «х».
Ð=
1
2
3
4
5
6
7
8
2
–1
1
1
0
0
0
0
0
4
0
0
–1
1
0
0
1
0
6
0
0
1
0
Х
1
–1
0
8
0
0
–1
0
1
0
0
1
45.
Топологические матрицыРешение задания 7: Для приведенного варианта выбора
покрывающего дерева графа укажите значение элемента матрицы
главных контуров, отмеченного символом «х».
ì1, j - ÿ âåò âü í àï ðàâëåí à ñî ãëàñí î ñ i - ì êî í ò óðî ì
ï
rij = í-1, j - ÿ âåò âü í àï ðàâëåí à ï ðî ò èâî ï î ëî æ í î i - ì ó êî í ò óðó
ï0, j - ÿ âåò âü í å èí öèäåí ò í à i - ì ó êî í ò óðó
î
Ð=
Правильный ответ на задание 7: – 1
1
2
3
4
5
6
7
8
2
–1
1
1
0
0
0
0
0
4
0
0
–1
1
0
0
1
0
6
0
0
1
0
–1
1
–1
0
8
0
0
–1
0
1
0
0
1
46.
Топологические уравненияСтруктура полюсного графа электронной схемы может быть описана
алгебраически с использованием топологических уравнений. Топологические
уравнения полюсных графов электронных схем выражаются законами Кирхгофа.
Топологические уравнения в матричной форме записываются с использованием
топологических матриц полюсных графов электронных схем.
Матричная форма системы n = u - n независимых уравнений,
соответствующих первому закону Кирхгофа, имеет вид:
é Iâ1 ù
êI ú
где I â = ê â2 ú
ê××× ú
ê ú
ë Iâ l û
Ï I â = 0,
– вектор токов всех
l
ветвей схемы (ребер графа).
47.
Топологические уравненияМатричная форма системы
s = l -u + n
независимых уравнений,
соответствующих первому закону Кирхгофа, имеет вид:
ÐU â = 0,
é U â1 ù
êU ú
â2 ú
где U â = ê
– вектор токов всех
ê××× ú
ê
ú
U
ë âl û
l
ветвей схемы (ребер графа).
Поскольку топологические уравнения записываются относительно
системы независимых сечений и циклов, то сечения и циклы можно
рассматривать как некоторую систему координат.
48.
Пример реализации с использованием MathcadÏàðàìåòðû êîìïîíåíòîâ
3
rá = 100
rñ = 1× 10
3
rê = 10
rý = 5
= 60
Rí = 1× 10
6
R1× R2
Рис. 2.11 – Схема эмиттерного
повторителя
Rý( p ) =
R1 + R2
3
+
1
p × C1
-6
C1 = 10× 10
-6
C2 = 10× 10
3
R2 = 15× 10
R3 = 30× 10
3
R4 = 30× 10
1
×
R1 + R2 p × C1
R1× R2
3
R1 = 15× 10
Zk( p ) =
-6
C3 = 10× 10
- 12
Cê = 3× 10
1
rê×
p × Cê
1
rê +
p × Cê
a =
+1
49.
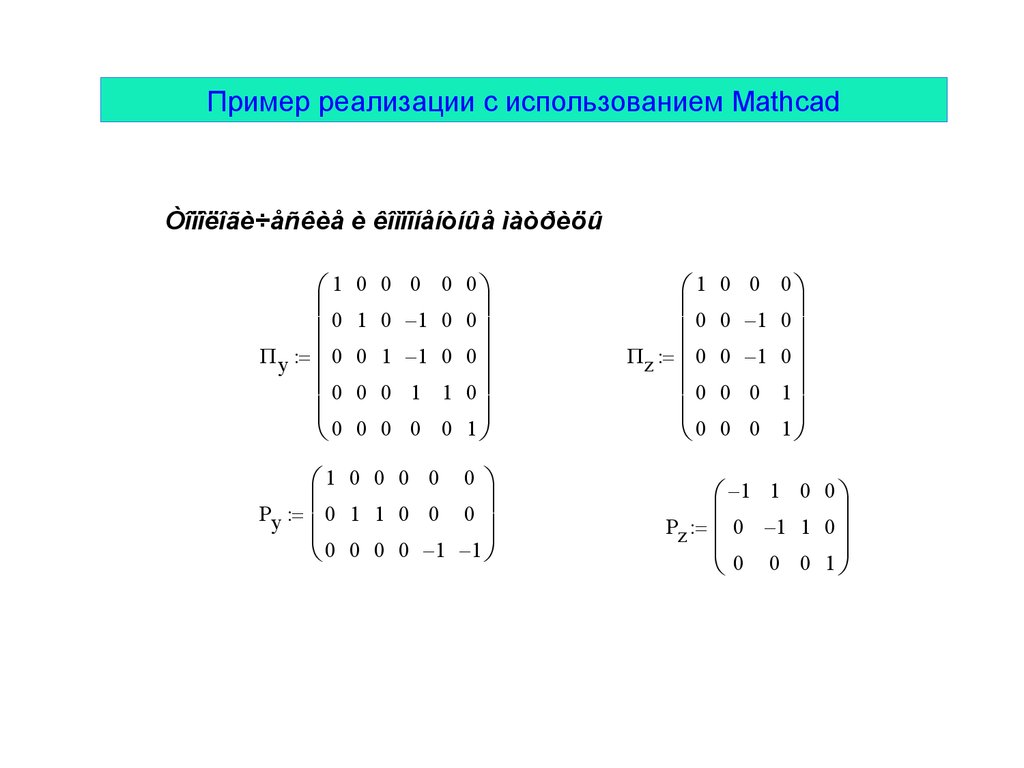
Пример реализации с использованием MathcadÒîïîëîãè÷åñêèå è êîìïîíåíòíûå ìàòðèöû
1
0
y = 0
0
0
0 0 0 0 0
0 1 -1 0 0
0 0 1 1 0
0 0 0 0 1
1 0 -1 0 0
1 0 0 0 0 0
Py = 0 1 1 0 0 0
0
0
0
0
1
1
1
0
z = 0
0
0
0 0 0
0 -1 0
0 0 1
0 0 1
0 -1 0
-1 1 0 0
Pz = 0 -1 1 0
0 0 0 1
50.
Пример реализации с использованием MathcadÒîïîëîãè÷åñêèå è êîìïîíåíòíûå ìàòðèöû
p× C2
0
0
Yb ( p ) =
0
0
0
0
1
rá
0
0
0
0
0
0
0
0
1
Rý( p )
0
0
1
Zk( p )
0
0
0
0
0
0
0
0
1
R3
0
0
0
0
0
p × C3
0
rñ
0
Zb ( p ) =
0
0
0
0
0
R4 0
0
0 rý 0
0
0 Rí
51.
Пример реализации с использованием MathcadÒîïîëîãè÷åñêèå è êîìïîíåíòíûå ìàòðèöû
0
0
0
N =
0
0
0
0 0 0
0 0 0
0 0
0 a
0 0
0 0
0
0
M =
0
0
0
0
0
0
T
Lz = 4
u = 7
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
T
Jb = ( 0 0 0 0 )
Ly = 6
0 0 0 0 0
Eb = ( 1 0 0 0 0 )
n = 1
ny = 2
v = u - n
v'' = ny - n
v' = v - v''
s = ( Ly + Lz) - u + n
s'' = Ly - u + ny
s' = s - s''
= v + s
'' = v'' + s''
' = v' + s'
52.
Пример реализации с использованием MathcadÎáîáùåííûå òîïîëîãè÷åñêèå ìàòðèöû
f( x y ) = 0
= stack augment y matrix( v' Lz f) augment matrix s' Ly f Pz
0
1
2
3
4
5
6
7
8
9
0
1
0
0
0
0
0
0
0
0
0
1
0
1
0
-1
0
0
0
0
0
0
2
0
0
1
-1
0
0
0
0
0
0
= 3
0
0
0
1
1
0
0
0
0
0
4
0
0
0
0
0
1
0
0
0
0
5
0
0
0
0
0
0
-1
1
0
0
6
0
0
0
0
0
0
0
-1
1
0
7
0
0
0
0
0
0
0
0
0
1
53.
Пример реализации с использованием MathcadÎáîáùåííûå òîïîëîãè÷åñêèå ìàòðèöû
1 = stack augment matrix( v' Ly f) z augment Py matrix s' Lz f
0
1
2
3
4
5
6
7
8
9
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
-1
0
2
0
0
0
0
0
0
0
0
-1
0
1 = 3
0
0
0
0
0
0
0
0
0
1
4
0
0
0
0
0
0
0
0
0
1
5
1
0
0
0
0
0
0
0
0
0
6
0
1
1
0
0
0
0
0
0
0
7
0
0
0
0
-1
-1
0
0
0
0
54.
Пример реализации с использованием MathcadÎáîáùåííàÿ êîìïîíåíòíàÿ ìàòðèöà
V( p ) = stack augment Yb ( p ) N augment M Zb ( p )
Ìàòðèöà ýêâèâàëåíòíûõ ïàðàìåòðîâ ñõåìû
T
T
W ( p ) = × V( p ) × + 1×
Ñòîëáöû ìàòðèöû íåâûðîæäåííûõ êîíòóðîâ,
ñîîòâåòñòâóþùèå âõîäíîìó è âûõîäíîìó ðåáðàì
0
Pin = Pz
3
Pout = Pz
55.
Пример реализации с использованием MathcadÏðåîáðàçóþùèå âåêòîðû äëÿ ñóììàðíûõ àëãåáðàè÷åñêèõ
äîïîëíåíèé ìàòðèöû W
in = stack( matrix( v' 1 f) -Pin )
0
0
0
0
in =
0
1
0
0
T
in = augment matrix( 1 v' f) Pin
out = stack( matrix( v' 1 f) Pout )
0
in = ( 0 0 0 0 0 -1 0 0 )
0
0
0
out =
0
0
0
1
T
out = augment matrix( 1 v' f) Pout
out = ( 0 0 0 0 0 0 0 1 )
56.
Пример реализации с использованием MathcadÂñïîìîãàòåëüíûå ïðîãðàììû
Ïîäïðîãðàììà óäàëåíèÿ èç ìàòðèöû Ì à-îé ñòðîêè è â-îãî ñòîëáöà
Minor( M a b ) =
r -1
for i 0 rows ( M ) - 2
r r+ 1
r r + 1 if r
a-1
s -1
for j 0 cols ( M ) - 2
s s+1
s s + 1 if s
A
A
i j
M
r s
b-1
57.
Пример реализации с использованием MathcadÏîäïðîãðàììà îïðåäåëåíèÿ ïðîñòîãî àëãåáðàè÷åñêîãî äîïîëíåíèÿ ìàòðèöû Ì
Cofactor( M a b ) =
A Minor( M a b )
( -1)
a+ b
× A
Ïîäïðîãðàììà óäàëåíèÿ èç ìàòðèöû Ì à-îé è ñ-îé ñòðîê, b-îãî è d-îãî ñòîëáöà
MinorDouble( M a b c d ) =
A Minor( M a b )
p
c - 1 if a c
c otherwise
q
d - 1 if b d
d otherwise
Minor( A p q )
58.
Пример реализации с использованием MathcadÏîäïðîãðàììà îïðåäåëåíèÿ äâóõêðàòíîãî àëãåáðàè÷åñêîãî äîïîëíåíèÿ ìàòðèöû Ì
CofactorDouble( M a b c d ) =
A MinorDouble ( M a b c d )
0 if ( a c) ( b d ) ( a c) ( b d )
1 otherwise
( -1)
a+ b+ c+ d+
× A
Ïîäïðîãðàììà ïðåîáðàçîâàíèÿ ìàòðèöû W â ñîîòâåòñòâèè ñ ïðåîáðàçóþùèìè
âåêòîðàìè = th и = lam
SumMinor( W th lam) =
T
Wr W
for i 2 length ( th ) - 1
thi-1
thi- 1
th1-1
Wr
Wr
+ Wr
if i th
if length ( th ) 2
0
thi-1
thi- 1
th -1
Wr
Wr
- Wr 1
otherwise
T
Wr Wr
for i 2 length ( lam) - 1
lami-1
lami- 1
lam1-1
Wr
Wr
+ Wr
if i lam
0
lami-1
lami- 1
lam1-1
Wr
Wr
- Wr
otherwise
Wr
if length ( lam) 2
59.
Пример реализации с использованием MathcadÎïðåäåëåíèå ñóìàðíîãî àëãåáðàè÷åñêîãî äîïîëíåíèÿ D(ql)
ìàòðèöû W (q = th, l = lam)
SumCofactor( W th lam) = ( -1)
th1+ lam1
× sign th × lam × Minor SumMinor( W th lam) th lam
0
0
Ïîäïðîãðàììà âûäåëåíèÿ ñîáñòâåííûõ ïîäìíîæåñòâ ýëåìåíòîâ ïðåîáðàçóþùèõ
âåêòîðîâ q1 = th1, q2 = th2
Sobstv ( th1 th2) =
k 0
for i 1 last ( th1)
f 1
for j 1 last( th2)
f 0 if th1
i
if f
Sth1 i
k
k k+ 1
Sth1
th2
j
1
1
60.
Пример реализации с использованием MathcadÏîäïðîãðàììà ïåðåãðóïèðîâêè ýëåìåíòîâ ïðåîáðàçóþùåãî âåêòîðà q = th
â ñîîòâåòñòâèè ñ âûáîðîì îïîðíîãî ýëåìåíòà ñ íîìåðîì q
Perest ( th q ) =
v th
v th
1
v th
q
q
1
if q th
0
otherwise
v -sign th × length ( th ) - 1 - th
0
0
k 1
for i 1 length ( th ) - 2 - th
k k + 1 if
v
i+ 1
th
th
0
+i
q
th0 + k
k k+ 1
for i 1 th
v
v
0
i+ length( th) - 1- th0
th
0
i
0
if length ( th ) - 2 - th
0
1
61.
Пример реализации с использованием MathcadÏîäïðîãðàììà ðàñïðåäåëåíèÿ ýëåìåíòîâ ïðåîáðàçóþùåãî âåêòîðà
ïî ïîäìíîæåñòâàì ïîëîæèòåëüíûõ è îòðèöàòåëüíûõ ýëåìåíòîâ
Converter( th) =
p 0
n 0
for i 0 length ( th ) - 1
if th
i
1
p p+1
vp
if th
i
i+ 1
p -1
-1
n n+1
vn
n- 1
i+ 1
stack( p vp ) if n
stack( -n vn ) if p
0
0
stack( p vp vn ) otherwise
q = th
62.
Пример реализации с использованием MathcadÏîäïðîãðàììà îïðåäåëåíèÿ äâóõêðàòíîãî ñóììàðíîãî àëãåáðàè÷åñêîãî
äîïîëíåíèÿ ìàòðèöû W
SumCofactorDouble( W th1 lam1 th2 lam2) =
v Sobstv ( th1 th2)
if IsArray ( v )
thp1 Perest th1 v
0
thp2 th2
otherwise
v Sobstv ( th2 th1)
if IsArray ( v)
thp1 Perest th2 v
0
thp2 th1
v Sobstv ( lam1 lam2)
if IsArray ( v )
lamp1 Perest lam1 v
0
lamp2 lam2
otherwise
v Sobstv ( lam2 lam1)
if IsArray ( v)
lamp1 Perest lam2 v
0
lamp2 lam1
A SumMinor( W thp1 lamp1)
A SumMinor( A thp2 lamp2)
A MinorDouble A thp1 lamp1 thp2 lamp2
1
0 if thp1 thp2
1
1
1
1
lamp11 lamp21 thp11 thp21 lamp11 lamp21
1
1 otherwise
( -1)
thp11+ lamp11+ thp21+ lamp21+
× sign thp1 × sign lamp1 × sign thp2 × sign lamp2 × A
0
0
0
0
63.
Пример реализации с использованием MathcadÌîäåëèðîâàíèå
Îïðåäåëåíèå êîýôôèöèåíòà ïåðåäà÷è ïî íàïðÿæåíèþ
kU( p ) = -
Rí × SumCofactor W ( p ) Converter in Converter out
T
W ( p ) + Rí × SumCofactor W ( p ) Converter out Converter out
Îïðåäåëåíèå À×Õ êîýôôèöèåíòà ïåðåäà÷è ïî íàïðÿæåíèþ
A U = kU i×
T
64.
Пример реализации с использованием Mathcadlw = 0 0.1 10
0.8
0.6
AU 10
0.4
lw
0.2
1
10
100
1 10
3
1 10
4
5
1 10
10
6
1 10
7
1 10
1 10
8
1 10
9
1 10
10
lw
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) коэффициента
передачи по напряжению эмиттерного повторителя (рис. 2.11), в которой
использована высокочастотная Cê ¹ 0 схема замещения биполярного транзистора.
65.
Пример реализации с использованием Mathcadlw = 0 0.1 9
0.8
0.6
0.4
lw
AU 10
0.2
1
10
100
3
1 10
1 10
4
5
1 10
10
6
1 10
7
1 10
8
1 10
9
1 10
lw
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) коэффициента
передачи по напряжению эмиттерного повторителя (рис. 2.11), в которой
использована низкочастотная Cê = 0 схема замещения биполярного транзистора.
66.
.Вопросы для
. самоконтроля
1. При каком количестве ребер графа число независимых сечений и контуров
будут совпадать, если число вершин
u = 4 , а число компонентов n = 1.
2. При каком количестве вершин графа число независимых сечений и контуров
будут совпадать, если число ребер
= 8,
а число компонентов
n = 1.
3. При каком количестве компонентов графа число независимых сечений и
контуров будут совпадать, если число ребер = 12 , а число вершин
4. Определите значение элемента
p32
u = 9.
матрицы главных сечений для хорд,
соответствующей представленной матрице главных циклов для ребер дерева.
é - 1 1 0ù
r=ê
ú
ë- 1 1 - 1û
.
67.
Рекомендуемая литература1. Легостаев Н.С. Методы анализа и расчета электронных схем:
учебное пособие / Н.С. Легостаев, К.В. Четвергов. – Томск: Эль Контент,
2013. – 158 с. ISBN 978-5-4332-0076-0
2. Легостаев Н.С. Методы анализа и расчета электронных схем:
руководство к организации самостоятельной работы /
Н.С. Легостаев, К.В. Четвергов. – Томск: Томский государственный
университет систем управления и радиоэлектроники , 2006. – 215 с.
3. Легостаев Н.С. Методы анализа и расчета электронных схем:
учебное пособие / Н.С. Легостаев, К.В. Четвергов. – Томск: Томский
государственный университет систем управления и радиоэлектроники,
2006. – 110 с. ISBN 5-86889-304-2
68.
Спасибо за вниманиеВопросы и пожелания можно присылать через диспетчерский отдел ФДО.
Следующее занятие будет посвящено формированию матрично-векторных
параметров узловых и контурных уравнений методом эквивалентных схем.
Для подготовки к занятию изучите материал, представленный в разделе
2.3 учебного пособия на страницах 51-56.
Постарайтесь запомнить этапы формирования матричновекторных параметров и физический смысл собственной
i , взаимной проводимости yij узлов i, j ,
собственного сопротивления zkk контура k , взаимного
сопротивления z контуров k , s .
ks
проводимости
yii
узла

































































 Электроника
Электроника








