Распределения молекул по скоростям и энергиям

1.

Курс общей физики НИЯУ МИФИ
Основы молекулярной и статистической
физики
Семинары 23.04.2021
Распределения молекул
по скоростям и энергиям.
Лектор: Доцент НИЯУ МИФИ, к.ф.-м.н.,
Ольчак Андрей Станиславович

2.

Предшествующее ДЗ:
3.1.11-16, 20-21

3.

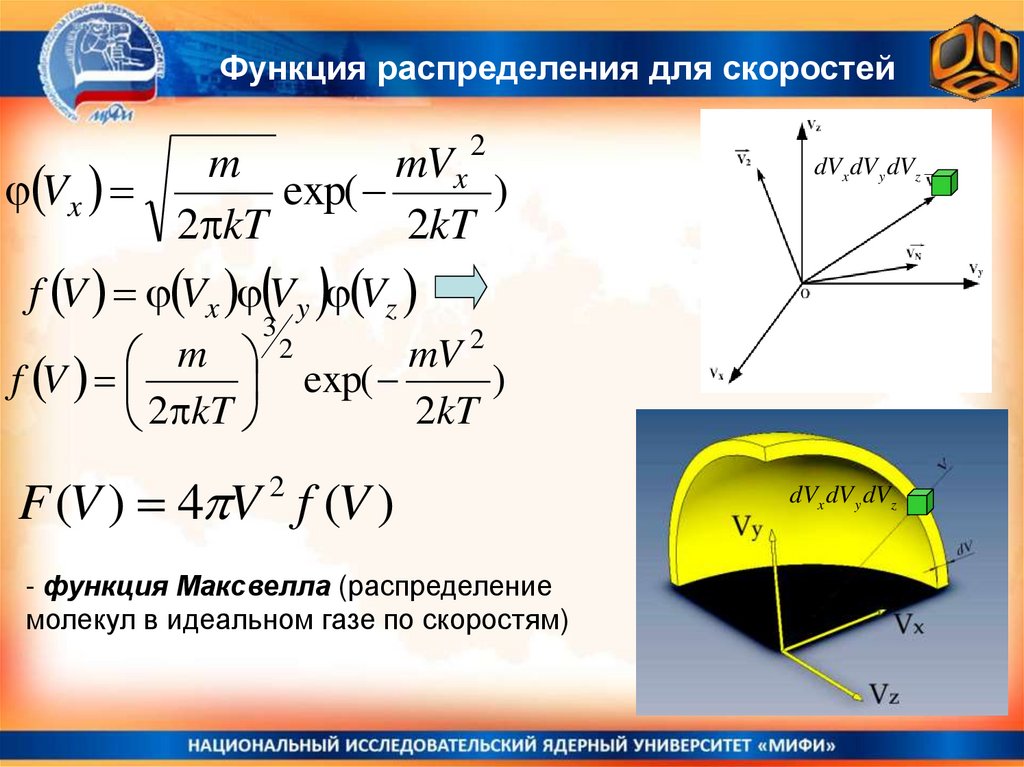
Функция распределения для скоростей
Вероятность того, что х-компонента скорости
молекулы лежит в интервале от vх до
dP(vх, vх + dvх) =
vх + dvх
φ(v2х)dvх
dVx dV y dVz
ВАЖНО! Из соображений симметрии функция φ(v2х)
должна быть четной, т.е. φ(vх)
-> φ(v2х)
Вероятность того, что вектор скорости молекулы
«попадает в кубик» dxdydz
вычисляется
по
правилу
вероятностей независимых событий:
вблизи v
умножения
dP(v) = φ(v2х)φ(v2y)φ(v2z)dvхdvydvz = f(v2)dvхdvydvz
ВАЖНО! Из соображений симметрии функция f(v) не должна зависеть от
направления скорости, а только от ее величины (или от ее квадрата)
f(v) -> f(v2) = φ(v2х)φ(v2y)φ(v2z)

4.

Функция распределения для скоростей
ВАЖНО: Функция распределения по скоростям
молекул зависит только от модуля (квадрата
модуля) скорости и равна произведению трех
функций распределения по квадратам компонентов
этой скорости:
dVx dV y dVz
f(v2) = φ(vx2)φ(vy2)φ(vz2)
Единственная математическая функция, обладающая
таким свойством (произведение трех одинаковых
функций от разных аргументов равно функции от суммы
их аргументов) - это экспонента!
exp(avx2)exp(avy2)exp(avz2)=exp(a(vx2+vy2+vz2)) = exp(av2)
Запишем эти функции распределения и их параметры в виде:
φ(vx2) = Аexp(-avx2/2); f(v2) =A3exp(-av2/2);
где a>0 обязательно, ибо с ростом v функции распределения не должны
неограниченно расти

5.

Функция распределения для скоростей
φ(vx2) = Аexp(-avx2/2);
где a>0
Условие нормировки:
2
exp(
Х
)dХ
Vx dVx 1
А = (a/2π)½
- интеграл Пуассона
f(v) =A3exp(-av2/2)
dVx dV y dVz

6.

Функция распределения для скоростей
φ(vx) = (a/2π)½ exp(-avx2/2);
где a>0
Найдем среднее значение квадрата скорости молекулы:
Vx 2
2
V
2
x
Vx 2 Vx dVx
V
exp(
)dV
x
2
2
Этот интеграл тоже сводится к интегралу Пуассона.
<vx2>= 1/a; φ(vx) = (2π<vx2>)-½ exp(-vx2/2<vx2>);

7.

Функция распределения для скоростей
φ(vx) = (2π<vx2>)-½ exp(-vx2/2<vx2>)
Из закона равнораспределения энергии по степеням свободы следует:
mV x 2
m 2
1
Vx kT
2
2
2
Vx
2
kT / m
2
mVx
m
Vx
exp(
)
2 kT
2kT
f V Vx Vy Vz
m
f V
2 kT
3
2
mV 2
exp(
)
2kT
dVx dV y dVz

8.

Функция распределения для скоростей
2
mVx
m
Vx
exp(
)
2 kT
2kT
dVx dV y dVz
3
f V Vx Vy Vz
m
f V
2 kT
2
mV 2
exp(
)
2kT
F (V ) 4 V f (V )
2
- функция Максвелла (распределение
молекул в идеальном газе по скоростям)
dVx dV y dVz

9. Функция Максвелла для разных температур и масс молекул

3
mV 2
m 2
2
F V
2 kT
V Vвер
V Vвер
exp
4 V
2kT
F V V
2
T2
T1
2
m2
m1
mV 2
F V exp
2kT
Площадь под кривой ВСЕГДА
равна единице
2

10.

Три «средние скорости» молекул в газе
m
F V
1/2
Vвер = (2kT/m)
2 kT
Vср = (8kT/πm)1/2
Vср.кв = (3kT/m)1/2
Vср.кв.
3kT
m
>
3
2
mV 2
4 V 2
exp
2
kT
8kT
V
m
>
F(vвер)= 4π-1/2е-1 / vвер = 0,83/ vвер
F(<v>)= 16π-3/2е-(4/π)/ vвер = 0,804/ vвер
F(vcр.кв)= 6π-1/2е-3/2/ vвер = 0,76/ vвер
Vвер
2kT
m

11.

ПРИМЕР:
Пример: Смесь азота и кислорода находится при температуре
T = 300 K. Найти средние скорости молекул кислорода и азота.
VO
2
8kT
mO
2
VO
VN
2
2
VN
2
8kT
mN
8 8,31 300
3 м
м
0
,
45
10
450
с
с
3,14 32 10 3
8 8,31 300
3 м
0
,
48
10
480 м
3
с
с
3,14 28 10
2

12.

ПРИМЕР:
Пример: Какая примерно доля молекул газа имеет скорости в
интервале между
a) cамой вероятной и средней скоростью
Δv = <v> - vвер = (2/√π-1) vвер = 0,128 vвер << vвер
ΔP =~ F(vвер)Δv = ( 0,83/ vвер)0,128 vвер = 0,106
a) …средней и среднеквадратичной скоростью
Δv = vср.кв - <v> = (√ 1,5 -2/√π)vвер = 0,097 vвер << vвер
ΔP =~ F(<v>)Δv = ( 0,8/vвер)0,128 vвер = 0,1

13.

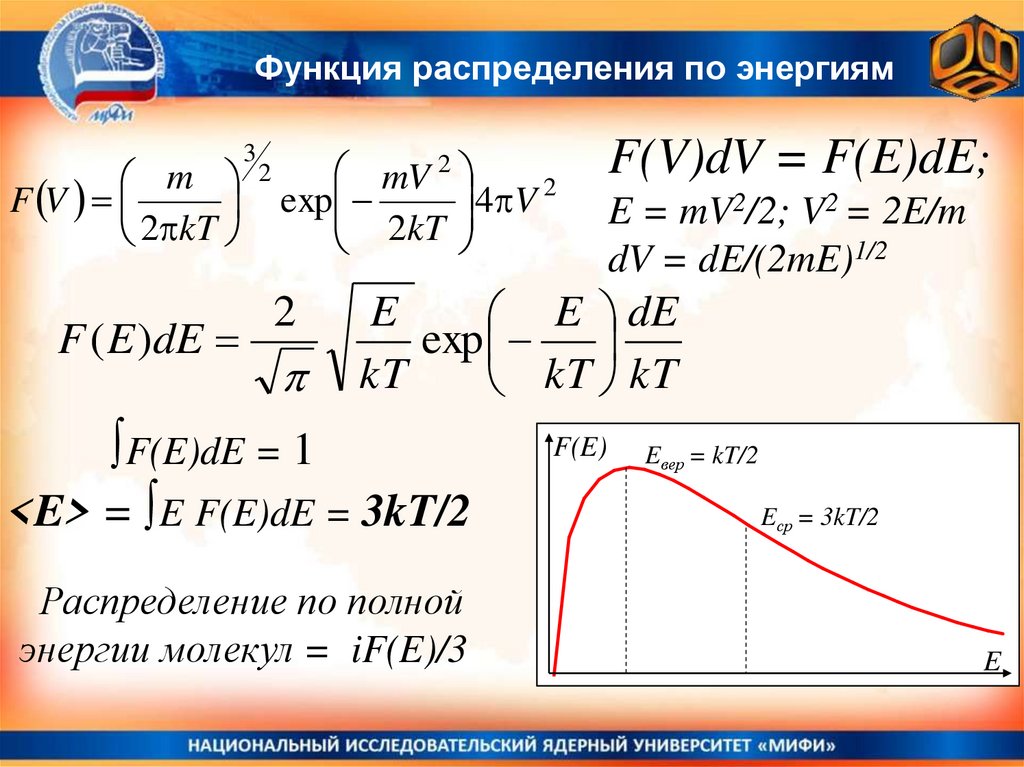
Функция распределения по энергиям
m
F V
2 kT
F ( E )dE
3
2
mV 2
4 V 2
exp
2
kT
2
F(V)dV = F(E)dE;
E = mV2/2; V2 = 2E/m
dV = dE/(2mE)1/2
E
E dE
exp
kT
kT kT
∫F(E)dE = 1
<E> = ∫E F(E)dE = 3kT/2
Распределение по полной
энергии молекул = iF(E)/3
F(E)
Eвер = kT/2
Eср = 3kT/2
E

14.

Функция распределения для энергий
F ( E )dE
2
E
E dE
exp
kT
kT kT
Если учесть, что в гравитационном поле Земли молекулы обладают еще и
= mv2/2 + mgy,
потенциальной энергией Е = Т + U
подставить в
выражение для распределения молнекeл по энергиям и проинтегрировать по
всем скоростям, можно получить отдельно распределение плотности числа
молекул по потенциальным энергиям – то есть, по высоте над поверхностью
Земли
n h n0 exp(
Это т.н. распределение Больцмана.
gh
RT
)

15.

Распределение Больцмана
Свойства
• Полное число молекул
газа неизменно
n h n0 exp(
N n dV n h Sdh
0
• Концентрация на
нулевой высоте
n0 = Nμg/SRT
• Концентрации для
различных температур
Если T2
> T1
то
n02 < n01
T2 > T1
gh
RT
)

16.

Распределение Больцмана
n h n0 exp(
gh
RT
p = nkT
)
Зависимость концентрации
молекул в атмосфере от
высоты - распределение
Больцмана.
p h p0 exp(
gh
RT
)
Зависимость давления от
высоты - барометрическая
формула.
p0 = n0kT = (M/S)g
M – масса столба атмосферы с основанием S
Атмосфера у поверхности Земли имеет давление ~105Па = 105Н/м2
ПРИМЕР 1. Высота, на которой давление (теоретически) понижается в
2 раза:
h = RTln2/μg ~> 6км

17.

Распределение Больцмана
n h n0 exp(
gh
RT
p = nkT
)
Зависимость концентрации
молекул в атмосфере от
высоты - распределение
Больцмана.
p h p0 exp(
gh
RT
)
Зависимость давления от
высоты - барометрическая
формула.
p0 = n0kT = (M/S)g
M – масса столба атмосферы с основанием S
Атмосфера у поверхности Земли имеет давление ~105Па = 105Н/м2
ПРИМЕР 2. Эффективная толщина атмосферы:
Hn0 = ∫dh n0exp(-μgh/RT) = n0RT/μg =>
=> H = RT/μg ~ 10км

18.

Парциальные давления в атмосфере
p h p0 exp(
gh
RT
)
ПРИМЕР:
p(h) = pN2 exp(- μNgh/RT) + pO2 exp(- μOgh/RT) + ..
p02(h)/pN2(h) = (21/78)exp((μN -μO)gh/RT)
На высоте ~10км
p02(h)/pN2(h) = 18/82

19.

Парциальные давления в атмосфере
n h n0 exp(
gh
RT
)
ПРИМЕР: пылинки массой 10-18 г взвешены в воздухе при
температуре 300 К. Во сколько раз концентрация пылинок на
высоте 10 метров меньше, чем у поверхности пола.
n(h)/n0 = exp(- mgh/kT) =~ e-25 ~ 10-11

20. Распределение Больцмана для дискретного энергетического спектра.

Число частиц с энергией Е
E
dN ~ exp( )dE
kT
В случае дискретного спектра энергий, число частиц в состоянии
Ei
N i A exp
kT
Нормировочная постоянная A определяется условием
Ei
N N i A exp
=>
kT
Ei
N exp
kT
Ni
Ei
exp kT

21.

Распределение Больцмана
для дискретного энергетического спектра.
Ei
N exp
kT
Ni
Ei
exp kT
Пример. Система состоящая из N молекул имеет температуру Т.
Энергия частиц может принимать два значения Е1=kT и Е2=2kT .
Найти число частиц в первом состоянии.
Решение. Используя распределение Больцмана для дискретного
энергетического спектра, получаем
E1
N exp
e
kT
N1
N
0,73 N
e 1
E1
E2
exp
exp
kT
kT

22.

ПРИМЕР:
Определить поток частиц , вытекающих из
поддерживаемого при постоянной температуре T сосуда
через небольшое отверстие радиуса R. Считать, что
числовая плотность частиц в сосуде равна n.
РЕШЕНИЕ: Направим ось x перпендикулярно
стенке в направлении вытекающего потока. Считая,
что покидающие сосуд молекулы в сечении отверстия
имеют положительные проекции скорости и обозначая
площадь отверстия S, получим
2
nS
mV
m
x
I S nVx
dVx
exp
2
2 kT
2kT
0
nS
2
1/2
x
2kT
2
2
exp
X
dX
m 0
n V
n V
2kT
2
exp( X )0
S
R2
m
4
4

23.

Новое ДЗ:
3.1.11-16, 20-21
3.2.1, 3--16, 20-21

24.

Курс общей физики НИЯУ МИФИ
СПАСИБО за ВНИМАНИЕ!