Похожие презентации:
Распределение молекул по скоростям
1.
1. Распределение молекул по2.
3.
4.
5.
6.
скоростям
Экспериментальная проверка
распределения Максвелла
Барометрическая формула
Распределение Больцмана
Опыты Перрена
Средняя длина свободного
пробега. Число столкновений
2.
1. Распределение молекул по скоростямЗакон Максвелла описывается некоторой функцией f(υ),
называемой функцией
распределения молекул по
скоростям.
dN ( )
,
Функция f(υ) определяет относительное
N
число молекул
скорости которых лежат в интервале от υ до υ+dυ, т.е.
dN ( )
f ( )d
N
f
dN ( )
f ( )
Nd
-Закон
распределен
m0
4
e
(1) ия молекул
идеального
2 kT
газа по
скоростям
где m0 – масса молекулы, k – постоянная
Больцмана
(распределен
3
2
m0 2
2
2 kT
3.
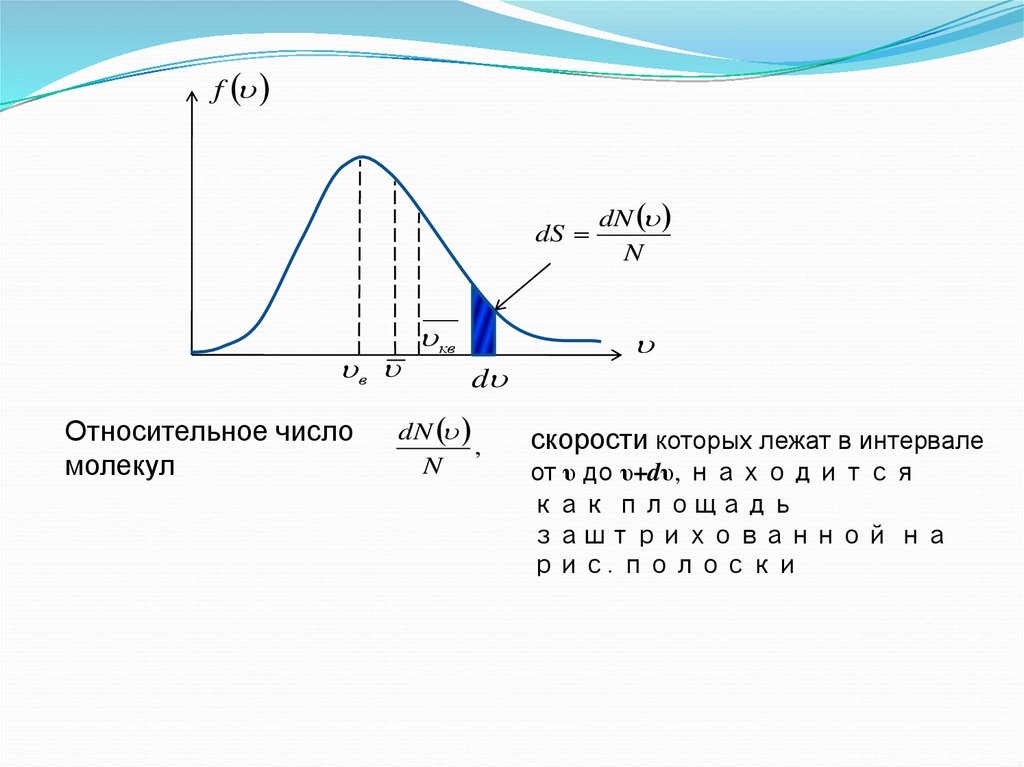
fdS
в
Относительное число
молекул
кв
d
dN
,
N
dN
N
скорости которых лежат в интервале
от υ до υ+dυ, находится
как площадь
заштрихованной на
рис. полоски
4.
Найдем значение наиболее вероятнойскорости υв , продифференцировав выражение
(1) по аргументу υ и приравняв
результат нулю.
df
m0
4
d
2 kT
2kT
в
m0
3
2
2 e
Т.к.
m0 2
2 kT
k
m0 2
d
e
2kT
R
NA
2
m0 2
2 kT
в
d 0
2 RT
5.
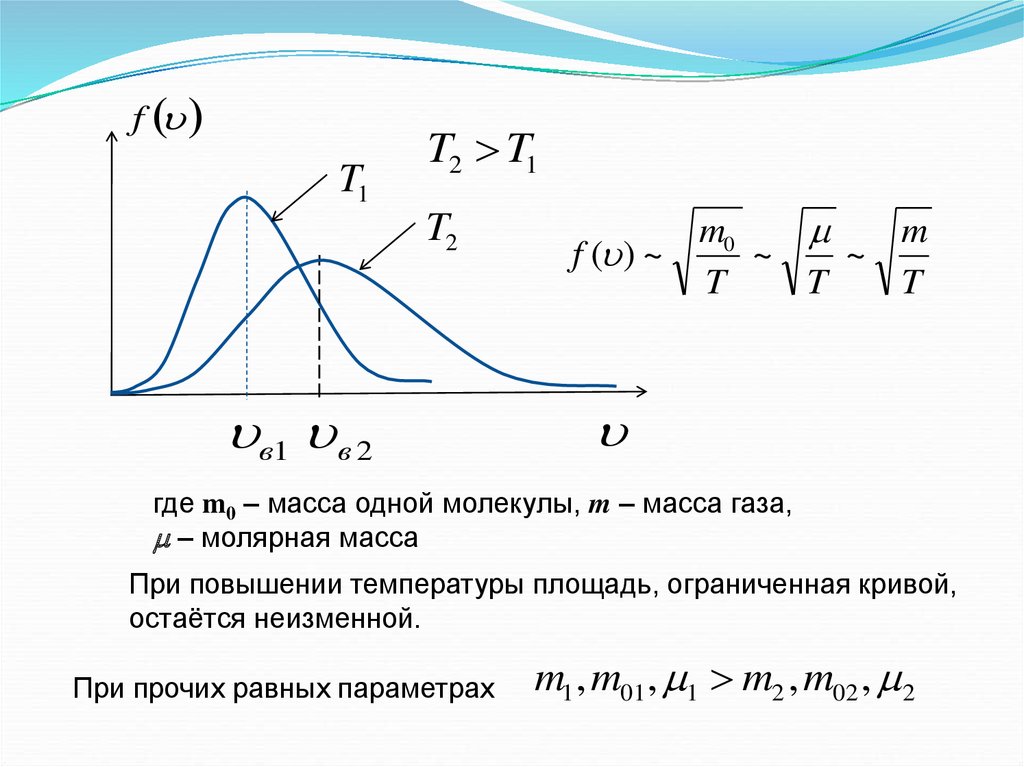
fT1
T2 T1
T2
в1 в 2
m0
m
f ( ) ~
~
~
T
T
T
где m0 – масса одной молекулы, m – масса газа,
– молярная масса
При повышении температуры площадь, ограниченная кривой,
остаётся неизменной.
При прочих равных параметрах
m1 , m01, 1 m2 , m02 , 2
6.
Cреднее значение скоростиКаждому интервалу
i
соответствует количество молекул
Ni f ( ) N i
N
i
i
- сумма значений скоростей всех N молекул.
N
i
N
f ( )d
0
i
f ( ) N
f ( )
N
i
i
i
8kT
m0
i
Средняя
арифметическая
скорость
Ni
7.
Скорости, характеризующие состояние газа:Наиболее вероятная скорость
Средняя
арифметическая
скорость
Средняя
квадратичная
скорость
2kT
в
m0
8kT
m0
3kT
m0
2
в
2 RT
8 RT
2
3RT
8.
2. Экспериментальная проверкараспределения Максвелла
Немецкий физик Штерн в
1920 г. экспериментально
определил скорости
молекул.
S R
t
S R t
Считая r <<R, можно положить
t
R
тогда
R
S
2
или
R 2
S
Измерив ΔS и ω, можно определить υ
9.
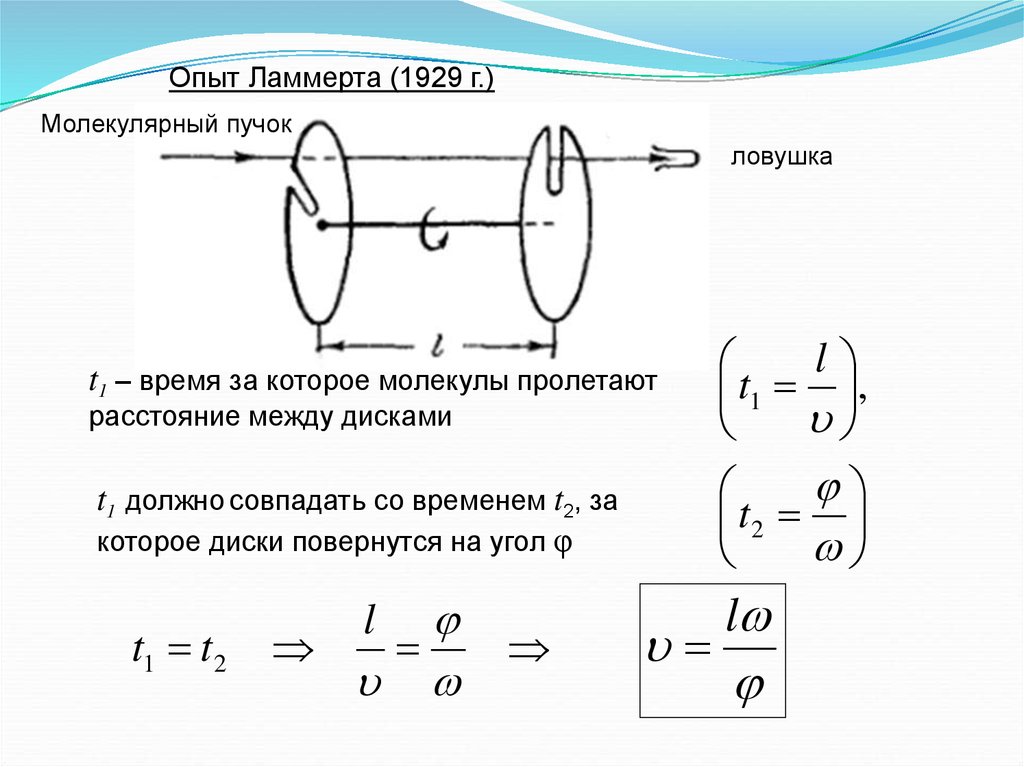
Опыт Ламмерта (1929 г.)Молекулярный пучок
ловушка
t1 – время за которое молекулы пролетают
l
t1 ,
t1 должно совпадать со временем t2, за
которое диски повернутся на угол φ
t2
расстояние между дисками
t1 t 2
l
l
10.
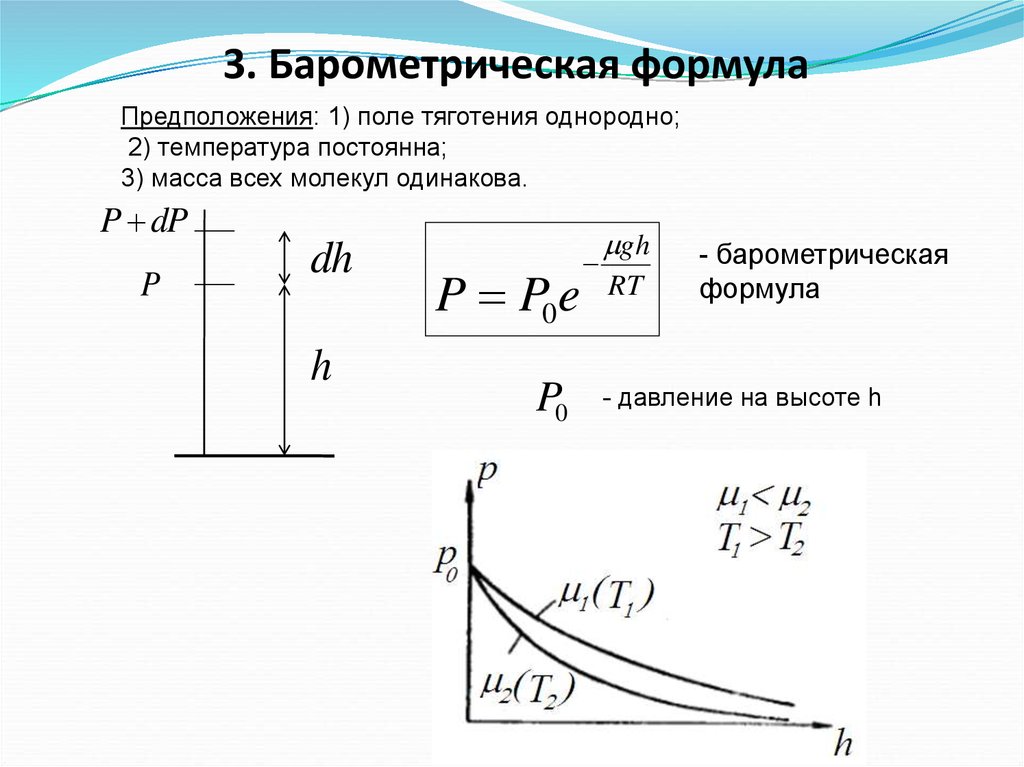
3. Барометрическая формулаПредположения: 1) поле тяготения однородно;
2) температура постоянна;
3) масса всех молекул одинакова.
P dP
P
dh
h
P P0 e
P0
gh
RT
- барометрическая
формула
- давление на высоте h
11.
4. Распределение БольцманаЗаменив в барометрической формуле
P nkT
получим закон изменения числа молекул в единице объема с высотой
n n0e
gh
RT
E p m0 gh
R
k
; m0
NA
NA
n n0e
Ep
kT
n n0 e
m0 gh
kT
Распределение
Больцмана
Две тенденции распределения молекул по высоте: 1)
притяжение молекул к Земле (чем больше m и меньше T);
2) тепловое движение стремится разбросать молекулы по
высоте.
12.
5. Опыты ПерренаПеррен (1909 г.) – опыты по определению числа Авогадро.
Рассмотрим слой, находящийся над дном кюветы на
высоте h.
Δh – толщина слоя.
Число частиц, попадающих в поле зрения микроскопа:
N n(h) S h
Распределение молекул по высоте
m0 g p
- вес броуновской частицы
N1 n0 e
N 2 n0 e
ph1
kT
S h
ph2
kT
S h
ln
n n0 e
n n0e
m0 gh
kT
ph
kT
N1
p ( h2 h1 )
N 2
kT
p(h2 h1 )
k
N1
T ln
N 2
R
N A
k
13.
6. Средняя длина свободного пробегаМежду двумя последовательными столкновениями
молекулы проходят некоторый путь l, который
называется длиной свободного пробега.
Минимальное расстояние, на которое сближаются при
столкновении центры двух молекул, называется
эффективным диаметром молекул d.
l
z
- средняя скорость
- среднее число соударений за 1 с
z 2n d
2
1
l
2 d 2 n
1
l
2 n
d 2
Эффективное
сечение молекул
14.
Явления переноса в термодинамическинеравновесных системах
•Диффузия
•Теплопроводность
•Вязкость
К явлениям переноса относятся
теплопроводность (обусловлена переносом
энергии), диффузия (обусловлена переносом
массы) и внутреннее трение (обусловлено
переносом импульса).
15.
1. Диффузия. Явление диффузии заключается в том, чтопроисходит
самопроизвольное
проникновение
и
перемешивание частиц двух соприкасающихся газов,
жидкостей и даже твердых тел; диффузия продолжается,
пока существует градиент плотности.
С макроскопической точки зрения перенос массы
вещества подчиняется закону Фика: масса вещества M,
переносимая за время t через площадку
S, прямо
пропорциональна градиенту плотности / x
M D
S t
x
[D]=м2/с
D — коэффициент диффузии.
Знак минус показывает, что перенос массы происходит в
направлении убывания плотности .
16.
Согласно кинетической теории газов:1
D l
3
l
- средняя длина свободного пробега
-средняя скорость движения молекул,
d – эффективный диаметр
n0 – концентрация молекул.
17.
2. Теплопроводность.Перенос энергии в форме теплоты
подчиняется закону Фурье:
Количество теплоты q, которое переносится в единицу
времени через площадку S в направлении нормали к
площадке, прямо пропорционально dT/dz — градиенту
температуры.
dT
— коэффициент
q
S теплопроводности
dz
Дж
м с град
[q]= Дж/с
Знак минус показывает, что при теплопроводности энергия
переносится в направлении убывания температуры
- плотность газа, сV – удельная
1
l cV теплоемкость газа при постоянном
3
объеме
18.
3. Внутреннее трение (вязкость). Механизм возникновениявнутреннего трения между параллельными слоями газа
(жидкости), движущимися с различными скоростями,
заключается в том, что из-за хаотического теплового движения
происходит обмен молекулами между слоями, в результате
чего импульс слоя, движущегося быстрее, уменьшается, а
движущегося медленнее — увеличивается, что приводит к
торможению слоя, движущегося быстрее, и ускорению слоя,
движущегося медленнее.
du
f
S
dz
Сила внутреннего трения между двумя
слоями газа (жидкости) подчиняется закону
Ньютона:
где — коэффициент вязкости, du/dz — градиент скорости,
показывающий быстроту изменения скорости в направлении z,
перпендикулярном направлению движения слоев, S — площадь, на
которую действует сила f.
Коэффициент вязкости вычисляется по формуле:
1
l
3
19.
Физические основы термодинамики1. Первое начало термодинамики.
2. Работа газа при изменении его объема.
3. Число степеней свободы молекулы. Закон
равномерного распределения энергии по
степеням свободы.
4. Теплоемкость идеального газа.
5. Адиабатический и политропический
процессы.
6. Работа, совершаемая идеальным газом при
различных процессах.
20.
1. Первое начало термодинамикиВнутренняя энергия может изменяться за счет двух
различных процессов:
1) Совершения над телом работы А’
2) Сообщения телу количества теплоты Q путем
теплопередачи
U U 2 U1
Q U A
Изменение внутренней энергии
Первое начало термодинамики
Теплота, передаваемая системе, расходуется на
увеличение ее внутренней энергии и на
совершение системой работы против внешних сил.
21.
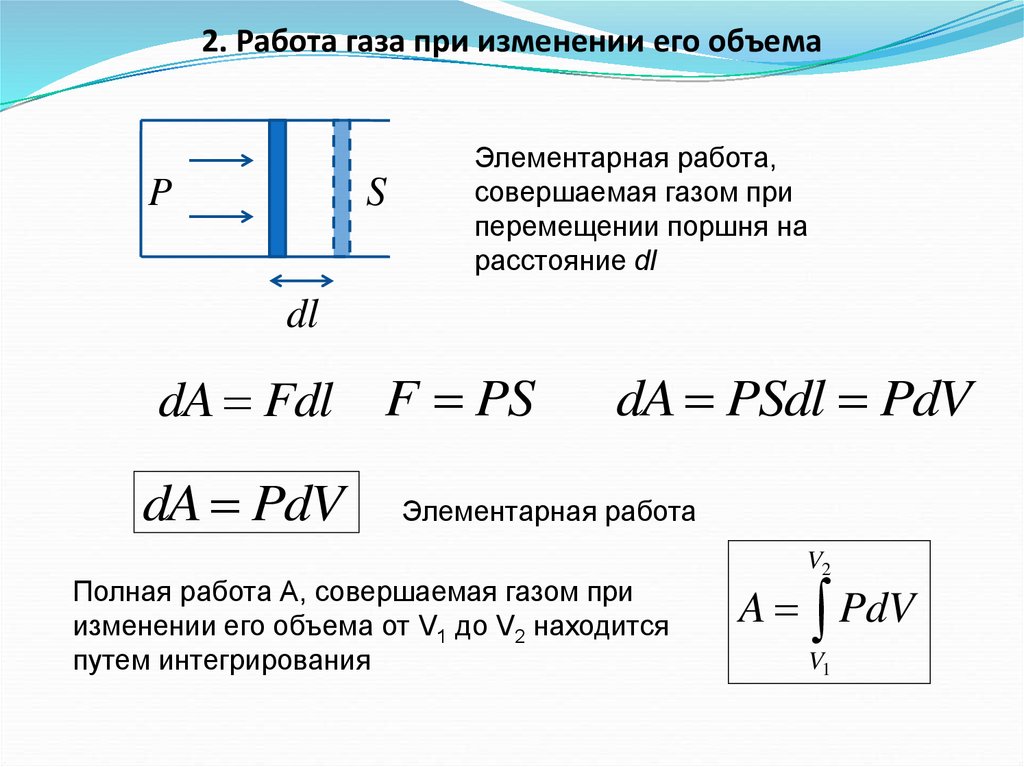
2. Работа газа при изменении его объемаS
P
Элементарная работа,
совершаемая газом при
перемещении поршня на
расстояние dl
dl
dA Fdl
dA PdV
F PS
dA PSdl PdV
Элементарная работа
Полная работа А, совершаемая газом при
изменении его объема от V1 до V2 находится
путем интегрирования
V2
A PdV
V1
22.
3. Число степеней свободы молекулы3
E kT
2
Средняя энергия поступательного движения
молекулы:
Числом степеней свободы механической системы называется
количество независимых величин, с помощью которых может быть
задано положение системы.
Средняя кинетическая энергия молекулы:
i
E kT
2
i iпост iвращ 2iколеб
i
i
U N A E N A kT RT
2
2
Внутренняя энергия 1 моля
идеального газа:
Внутренняя энергия произвольной массы газа:
U
m
U
mi
U
RT
2
23.
а) i=3б) i=5
в) i=6
y
x
z
Ни одна из поступательных степеней свободы не имеет
преимущества перед другими, поэтому на каждую из них
приходится в среднем одинаковая энергия, равная 1 E
т.к.
3
E kT
2
3
1
1
E1 E kT
3
2
1
E1 kT
2
24.
4.Теплоемкость идеального газаТеплоемкостью тела называется величина,
равная количеству тепла, которое нужно
сообщить телу, чтобы повысить его
температуру на один градус.
dQ
C
dT
Дж
C
К
Удельной теплоемкостью вещества
называется величина, равная количеству
теплоты, необходимому для нагревания
1 кг вещества на 1 градус.
dQ
c
mdT
Дж
c
кг К
C c
V const
молярная теплоемкость вещества (теплоемкость одного моля)
dV 0
i
U RT
2
A 0
dQV dU
i
CV R
2
dQV dU
CV
dT
dT
молярная теплоемкость при
постоянном объеме
25.
При нагревании газа при постоянном давлении его объем изменяется,сообщаемое газу количество теплоты идет не только на увеличение его
внутренней энергии, но и на совершение работы.
P const
dQP dU PdV
dV
dQP dU
Cp
P
dT
dT
dT P
dV
PV RT
C p CV P
dT P
C p CV R
i
CV R
2
dU
dT
CV
PdV RdT
P
dV
dT
R
Уравнение Майера
i
CP R R
2
i 2
CP
R
2
CP i 2
CV
i
молярная
теплоемкость при
постоянном
давлении
показатель адиабаты
26.
5. Адиабатический процессАдиабатическим называется процесс, протекающий
без теплообмена с внешней средой.
dQ dU PdV
m
PV
m
RT
dU
PdV VdP
PdV VdP
CV
PdV 0
m
R
C CV
VdP
P
PdV
CV
m
dQ 0
CV dT
CV dT PdV 0
m
1
m
(1)
RdT
dT
PdV VdP
m
R
Подставляем
в (1)
PdV VdP
R
PdV
CV
VdP
PdV
CP CV R
dP
dV
P
V
27.
ln P ln V constинтегрируем это уравнение
PV const
TV 1 const
Уравнение адиабаты. Уравнение Пуассона.
P
изотерма
адиабата
V
28.
Политропическим называется такой процесс, прикотором давление и объем идеального газа связаны
соотношением:
PV const
n
TV
n 1
const
n может принимать любые значения
n 0
n 1
n
n
Изобарический процесс
Изотермический процесс
Адиабатический процесс
Изохорический процесс
29.
6. Работа, совершаемая идеальным газом при различныхпроцессах
V2
A12 PdV
P1V1n
P n
V
PV n P1V1n
V1
V2
dV
A12 PV n
V
V1
n
1 1
Рассмотрим случай
dV
1 1
1
V V n n 1 V1n 1 V2n 1
1
V2
P1V1 V1
A12
1
n 1 V2
n 1
n 1
P1V1n 1
1
A12
n 1
n 1
n 1 V1
V2
n 1
m RT1 V1
A12
1
n 1 V2
Работа, совершаемая идеальным газом при любом политропическом
процессе, кроме изотермического (n=1)
30.
nДля адиабатического
процесса:
1
m RT1 V1
A12
1
1 V2
Для изотермического процесса: n=1
V2
A12 PdV
V1
m RT
P
V
m
V2
A12 RT ln
V1
При изобарическом
процессе:
При изохорическом
процессе:
m
V2
dV
A12 RT
V
V1
Работа, совершаемая газом при
изотермическом процессе
A12 p(V2 V1 )
A12 0
31.
Реальные газы1. Отклонение газов от идеальности
2. Уравнение Ван-дер-Ваальса
3. Экспериментальные изотермы
32.
1. Отклонение газов от идеальностиПоведение идеальных газов
описывается уравнением:
pV
m
RT
Fо- сила отталкивания; Fп – сила
притяжения; F – результирующая сила
При рассмотрении реальных газов
необходимо учитывать:
1. Взаимодействие молекул
2. Объем молекул
dA dEп
33.
Критерием различных агрегатных состояний веществаявляется соотношение величин En.min и kT
En.min - наименьшая потенциальная энергия взаимодействия
молекул – определяет работу против сил притяжения,
необходимую для того, чтобы разъединить молекулы,
находящиеся в равновесии (r=r0);
kT – определяет порядок средней кинетической энергии
хаотического теплового движения молекул.
1.
2.
3.
Если En.min << kT , то вещество находится в газообразном
состоянии
Если En.min >> kT , то вещество находится в твердом
состоянии
Если En.min ≈ kT , то вещество находится в жидком
состоянии
34.
2. Уравнение Ван-дер-Ваальса – уравнение состоянияреального газа
a
P
V b RT
2
V
a
p 2
V
a Н м
- дополнительное
давление
4
кмоль
м3
b
кмоль
Начиная с определенной,
своей для каждого
вещества температуры Ткр
при любом давлении
вещественным остается
только одно решение
уравнения. Температура
Ткр называется
критической.
35.
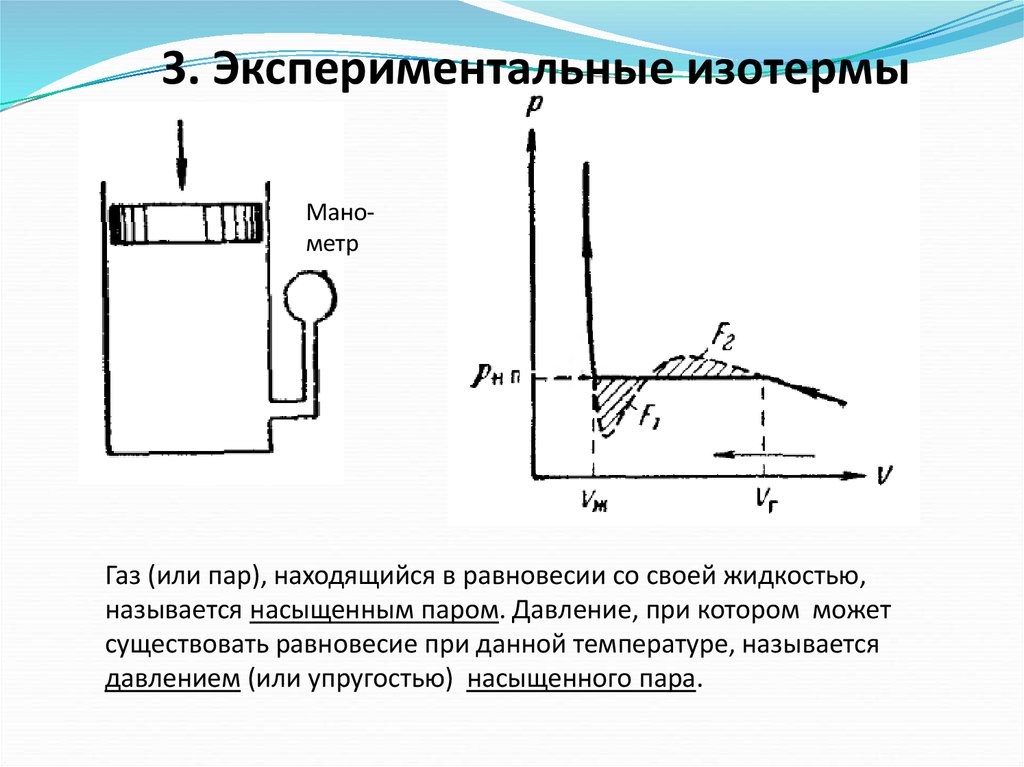
3. Экспериментальные изотермыМанометр
Газ (или пар), находящийся в равновесии со своей жидкостью,
называется насыщенным паром. Давление, при котором может
существовать равновесие при данной температуре, называется
давлением (или упругостью) насыщенного пара.
36.
Экспериментальные изотермы для нескольких значенийтемпературы
газ
жидкость
37.
1.Внутренняя энергия реального газа2.Эффект Джоуля-Томсона
3.Ожижение газов
38.
1. Внутренняя энергия реального газаВнутренняя энергия реального газа
Ek
U Ek E p
- кинетическая энергия движения молекул;
- взаимная потенциальная энергия молекул
Ep
Кинетическая энергия молекул, содержащихся в моле газа равна:
dA pi dV
pi
Ek cV T
Работа против внутренних сил идет на
увеличение потенциальной энергии
системы
- внутреннее давление
a
dE p pi dV 2 dV
V
a
U cV T
V
Интегрируем:
a
Ep
V
- Внутренняя энергия реального газа
39.
2. Эффект Джоуля-ТомсонаПропуская газ по теплоизолированной трубке с
пористой перегородкой, Джоуль и Томсон
обнаружили, что при расширении, которым
сопровождается
прохождение
газа
через
перегородку, температура
его несколько
изменяется. В зависимости от начальных
давления
и
температуры
изменение
температуры ΔТ имеет тот или иной знак и, в
частности, может оказаться равным нулю. Это
явление получило название эффекта ДжоуляТомсона.
40.
При адиабатическом расширении газа:U 2 U1 A
Работа совершаемая над порцией газа :
A p1Sl1 p2 Sl2
A p1V1 p2V2
U 2 U1 p1V1 p2V2 U1 p1V1 U 2 p2V2
U+pV - энтальпия – величина, которая сохраняется в
условиях опыта Джоуля-Томсона
(*)
41.
После расширения газ можно считать идеальным.Расчет для моля газа
p2V2 RT2
U 2 cV T2
Из уравнения Ван дер Ваальса для газа до расширения:
a
p1 2 (V1 b) RT1
V1
RT1
a
p1
2
V1 b V1
a
RT1
p1 2
V1 V1 b
RT1
a
p1V1
2 V1
V1 b V1
Внутренняя энергия до расширения:
a
U1 cV T1
V1
Подставив в (*) , получим:
a RT1
a
cV T1
2 V1 cV T2 RT2
V1 V1 b V1
42.
a RT1V1 acV T1
cV T2 RT2
V1 V1 b V1
Преобразуем третье слагаемое:
RT1V1 RT1 (V1 b b) RT1 (V1 b) RT1b
RT1b
RT1
V1 b
V1 b
V1 b
V1 b
подставим
a
RT1b a
cV T1 RT1
cV T2 RT2
V1
V1 b V1
Преобразуем:
(cV R)T1
RT1b 2a
(cV R)T2
V1 b V1
RT1b 2a
(cV R)(T2 T1 )
V1 b V1
RT1b 2a
1
T
(cV R) V1 b V1
Знак ΔТ определяется знаком выражения в скобках
43.
ΔТ=0 приRT1b 2a
0
V1 b V1
RT1b 2a
V1 b V1
2a(V1 b) V1RT1b
2a(V1 b) 2a b
1
T1
V1Rb
Rb V1
При
При
V1 b T1 0
2a
V1 T1
Rb
2a
T1
При
- эффект всегда отрицательный
bR
2a
При
- эффект положительный только при большом
T1
bR начальном объеме
44.
1.Обратимые и необратимыепроцессы. Коэффициент
полезного действия тепловой
машины.
2.Второе начало
термодинамики.
3.Цикл Карно. Коэффициент
полезного действия цикла
Карно для идеального газа.
45.
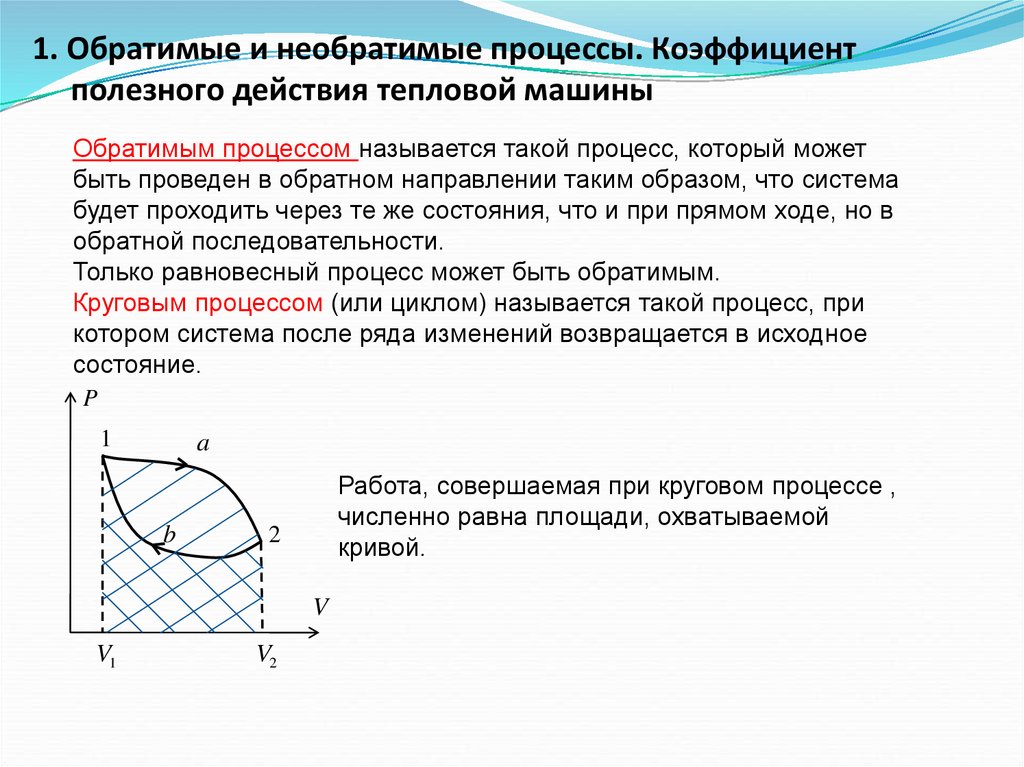
1. Обратимые и необратимые процессы. Коэффициентполезного действия тепловой машины
Обратимым процессом называется такой процесс, который может
быть проведен в обратном направлении таким образом, что система
будет проходить через те же состояния, что и при прямом ходе, но в
обратной последовательности.
Только равновесный процесс может быть обратимым.
Круговым процессом (или циклом) называется такой процесс, при
котором система после ряда изменений возвращается в исходное
состояние.
P
1
a
b
Работа, совершаемая при круговом процессе ,
численно равна площади, охватываемой
кривой.
2
V
V1
V2
46.
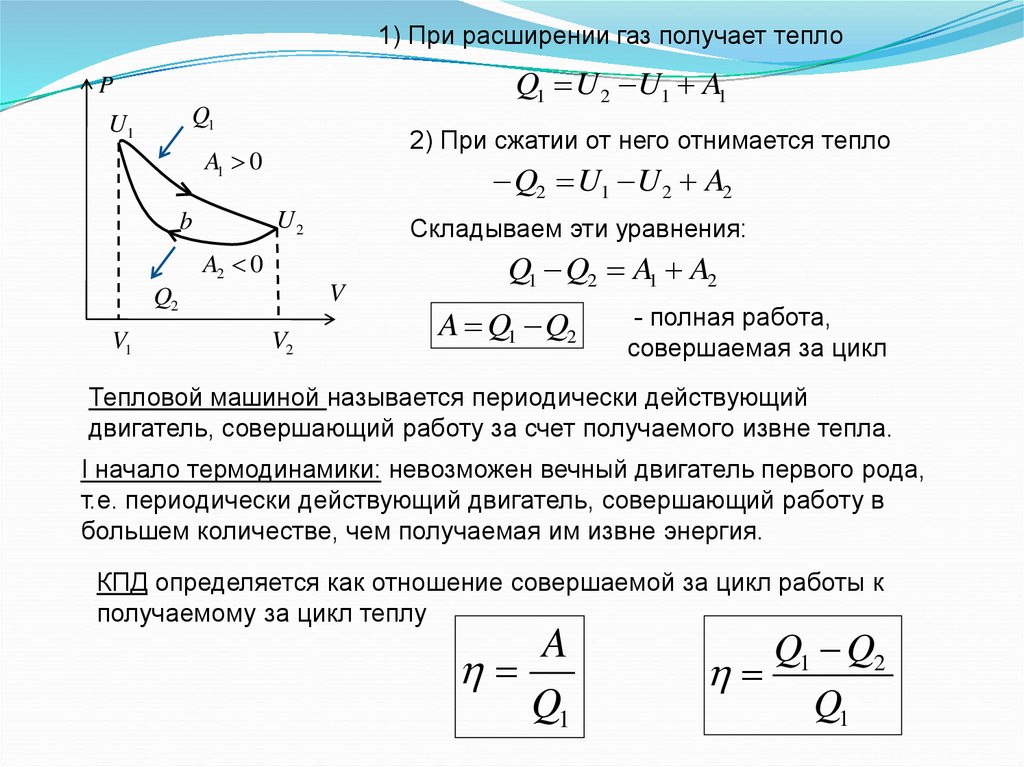
1) При расширении газ получает теплоQ1 U 2 U1 A1
P
Q1
U1
2) При сжатии от него отнимается тепло
A1 0
Q2 U1 U 2 A2
U2
b
Складываем эти уравнения:
A2 0
V
Q2
V1
V2
Q1 Q2 A1 A2
A Q1 Q2
- полная работа,
совершаемая за цикл
Тепловой машиной называется периодически действующий
двигатель, совершающий работу за счет получаемого извне тепла.
I начало термодинамики: невозможен вечный двигатель первого рода,
т.е. периодически действующий двигатель, совершающий работу в
большем количестве, чем получаемая им извне энергия.
КПД определяется как отношение совершаемой за цикл работы к
получаемому за цикл теплу
A
Q1
Q1 Q2
Q1
47.
2. Второе начало термодинамикиНевозможны такие процессы, единственным конечным результатом которых
был бы переход тепла от тела менее нагретого к телу более нагретому.
Невозможны такие процессы, единственным конечным результатом которых
явилось бы отнятие от некоторого тела определенного количества теплоты и
превращение его полностью в работу.
Невозможен вечный двигатель второго рода, т.е. такой периодически
действующий двигатель, который получал бы тепло от одного резервуара и
превращал бы его полностью в работу.
48.
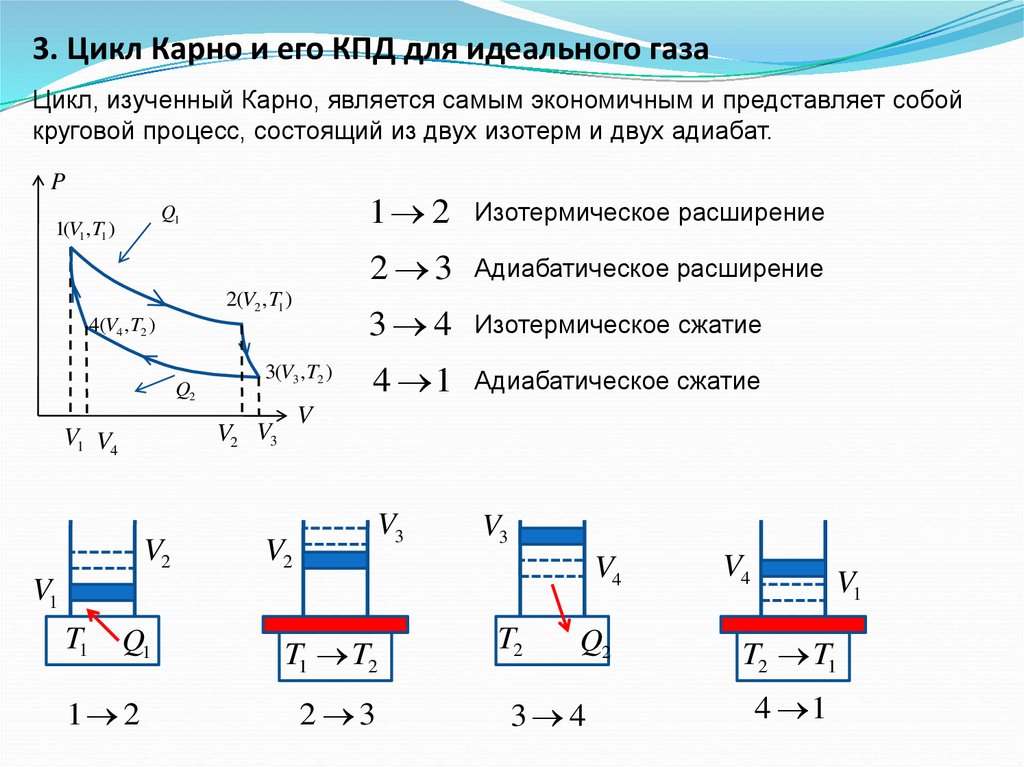
3. Цикл Карно и его КПД для идеального газаЦикл, изученный Карно, является самым экономичным и представляет собой
круговой процесс, состоящий из двух изотерм и двух адиабат.
P
Q1
1(V1 , T1 )
2(V2 , T1 )
4(V4 , T2 )
Q2
3(V3 , T2 )
V2
Изотермическое расширение
2 3
Адиабатическое расширение
3 4
Изотермическое сжатие
4 1
Адиабатическое сжатие
V3
V3
V
V2 V3
V1 V4
1 2
V2
V4
V1
T1
Q1
1 2
T1 T2
2 3
T2
Q2
3 4
V4
V1
T2 T1
4 1
49.
Q1 Q2Q1
Q1 - тепло получаемое за цикл от нагревателя
Q2 - тепло отдаваемое за цикл холодильнику
1 2 Q1 A12
1
2 3 T1V2
RT1 ln
V2
V1
1
T2V3
V2 1 V3 1
1
1
V1
V4
m
m
3 4 Q2 A34
4 1
m
RT2 ln
T1V1 1 T2V4 1
V2 V3
V1 V4
V2 m
V
RT2 ln 2
V1
V1 T1 T2
m
V2
T1
RT1 ln
V1
RT1 ln
T1 T2
T1
КПД цикла Карно зависит только от температуры нагревателя и
холодильника. Это выражение дает КПД любой обратимой машины.
V3
V4
50.
1.Неравенство Клаузиуса.2.Энтропия.
3.Свойства энтропии.
Теорема Нернста.
51.
1. Неравенство КлаузиусаКПД необратимой тепловой машины всегда меньше, чем
КПД обратимой.
Q2 ' T2
Q2 '
T2
Q1 Q2 ' T1 T2
1
1
Q1 T1
Q1
T1
Q1
T1
Q1 Q2 '
0
T1 T2
Q2 Q2 '
Q1 Q2
0
T1 T2
- Неравенство
Клаузиуса
Отношение количества тепла, полученного системой от
какого-либо тела к температуре этого тела, называется
приведенным количеством теплоты.
Если система совершает цикл, в ходе которого вступает в теплообмен
с двумя тепловыми резервуарами, температуры которых постоянны,
то сумма приведенных количеств тепла равна 0, если цикл обратим, и
меньше 0, если цикл необратим.
52.
2. Энтропия.Рассмотрим обратимый цикл.
2
I
1
II
Q
Q
0
1 2 T
2 1 T
(I )
( II )
Q
Q
1 2 T
1 2 T
(I )
( II )
Сумма приведенных количеств тепла, полученных
системой при обратимом переходе из одного состояния в
другое, не зависит от пути, по которому совершался
переход , а зависит только от начального и конечного
состояний.
Q
При обратимом процессе
T
представляет собой приращение некоторой функции
состояния. Эта функция названа энтропией.
53.
QS
T обр
dQ
dS
T
Приращение энтропии равно элементарному количеству
тепла, получаемому обратимо системой извне, отнесенному
к температуре, при которой это тепло получается.
Сумма приращений энтропии должна быть равна разности
значений в конечном и начальном состояниях
2
2
dQ
1 T 1 dS S 2 S1
Энтропия – аддитивная величина.
54.
3. Свойства энтропии. Теорема Нернста.Рассмотрим цикл, состоящий из обратимой и необратимой ветвей
необр.
2
1 2
( необр)
1
Q
Q
0
T 2 1 T
( обр)
обр.
Q
S1 S 2 0
T
1 2
( необр)
Q
S 2 S1
Ранее получили
1 2 T
S 2 S1
1 2
( необр)
Q
T
Объединяя эти выражения, получим
( обр)
Q
S 2 S1
1 2 T
Для элементарного процесса:
Если система изолирована, т.е. не
обменивается теплом с внешней средой:
dQ
dS
T
S2 S1 0 или S 0
55.
Т.о., энтропия изолированной системы может только возрастать (если всистеме протекает необратимый процесс), либо оставаться постоянной (если
в системе протекает обратимый процесс).
Убывать энтропия изолированной системы не может.
Обратимый адиабатический процесс протекает при постоянной энтропии.
Если система отдает тепло внешним телам, энтропия системы
уменьшается.
Найдем изменение энтропии при обратимом изотермическом процессе
Q
S 2 S1
1 2 T
Вынося постоянную температуру Т за знак
суммы, получим:
( обр)
1
Q
S 2 S1 Q 12
T 1 2
T
где Q12 – количество теплоты, полученное
системой при обратимом изотермическом
переходе из состояния 1 в состояние 2.
56.
Теорема Нернста: при стремлении абсолютнойтемпературы к нулю, энтропия любого тела также
стремится к нулю.
lim S 0
T 0
T
Энтропия любого тела с температурой Т может
быть представлена в виде:
Формула Больцмана для энтропии:
dQ
S
T
0
S k ln W
Энтропия определяется логарифмом числа микросостояний, с
помощью которых может быть реализовано данное
макросостояние.
Для изолированной системы:
1. Энтропия не может убывать.
2. Предоставленная самой себе система переходит из менее
вероятных состояний в более вероятные.
57. Электростатика
1. Электрический заряд и его свойства2. Закон Кулона
3. Электрическое поле. Напряженность
поля. Поток вектора напряженности
4. Теорема Гаусса и ее применение к
вычислению напряженности поля
58.
1. Электрический заряд и его свойства1) Существование электрического заряда в двух видах
2) Квантование заряда
3) Закон сохранения заряда
N
q
i 1
Проводники
Диэлектрики
А
Кл
с
i
const
Полупроводники
Единица электрического заряда – Кулон (Кл) –
электрический заряд, проходящий через поперечное
сечение проводника при токе силой 1А за время 1с.
59.
2. Закон КулонаЗакон Кулона: Сила взаимодействия двух неподвижных
точечных зарядов, находящихся в вакууме,
пропорциональна величине каждого из зарядов и обратно
пропорциональна квадрату расстояния между ними.
Направление силы совпадает с прямой, проходящей через
заряды.
F –кулоновская сила
F k
q1 q2
r
2
k – коэффициент пропорциональности
q1; q2
r
- величины зарядов
- расстояние между зарядами
В системе СИ:
12 Ф
0 8,85 10
м
k
1
4 0
- электрическая постоянная
60.
q1q2F1 k 2
r
q1q2
F2 k 2
r
F1
F2
- закон Кулона в вакууме
- закон Кулона в среде
- диэлектрическая проницаемость среды
1 q1 q2 r
F
4 0 r 2 r
F
r
q2
q1
61.
3. Электрическое поле. Напряженность поля.Поток вектора напряженности
Всякий заряд изменяет свойства окружающего его
пространства – создает в нем электрическое поле.
F
E
qпр
Напряженностью электрического поля
называется векторная величина,
численно равная отношению силы,
действующей на положительный
точечный заряд, находящейся в
данной точке поля к величине этого
заряда.
Напряженность поля,
создаваемого точечным
зарядом:
E
1 q r
4 0 r 2 r
В
E
м
62.
EF
q
q
F
F qE
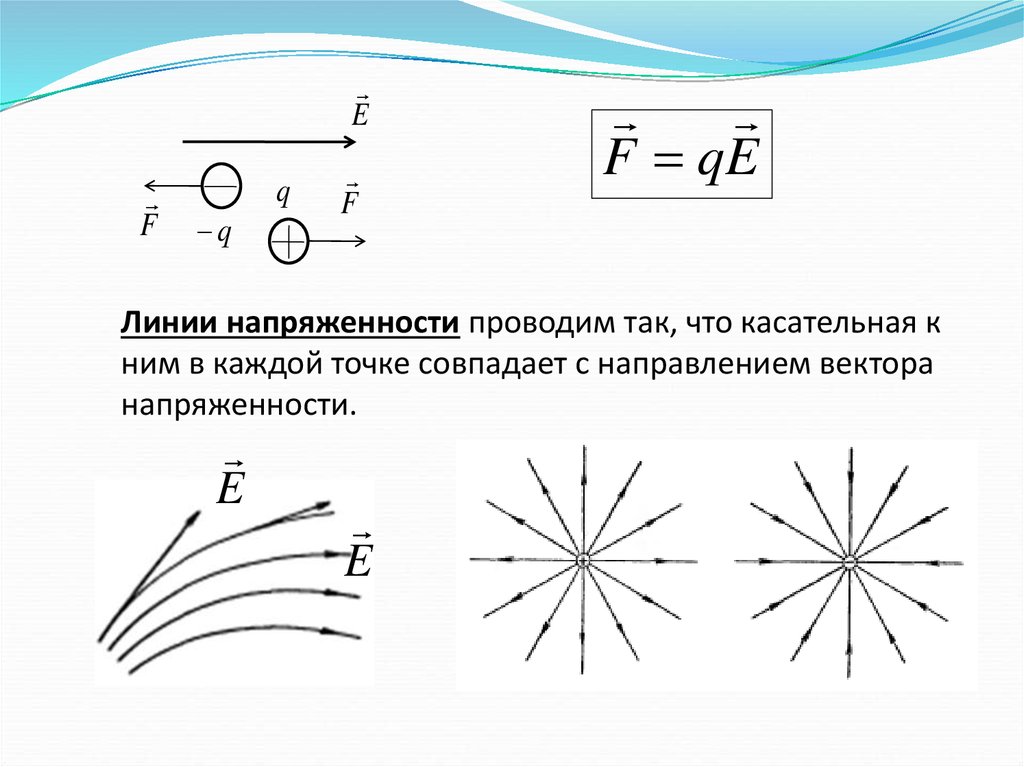
Линии напряженности проводим так, что касательная к
ним в каждой точке совпадает с направлением вектора
напряженности.
E
E
63.
qiq1
qi
A
A E1 E2
C
В точке С:
Ei
q2
E2
В точке А:
Ei
E2
E
E1
E E1 E2
E Е1 Е2 2Е1Е2соs
2
A
2
B
E1
В точке В:
E E1 E2
64.
Количество линий, пронизывающих площадкуdS
E
dS
n
EdS cos En dS
En
Поток вектора напряженности численно
равен количеству линий напряженности,
пронизывающих поверхность S
En dS
S
65.
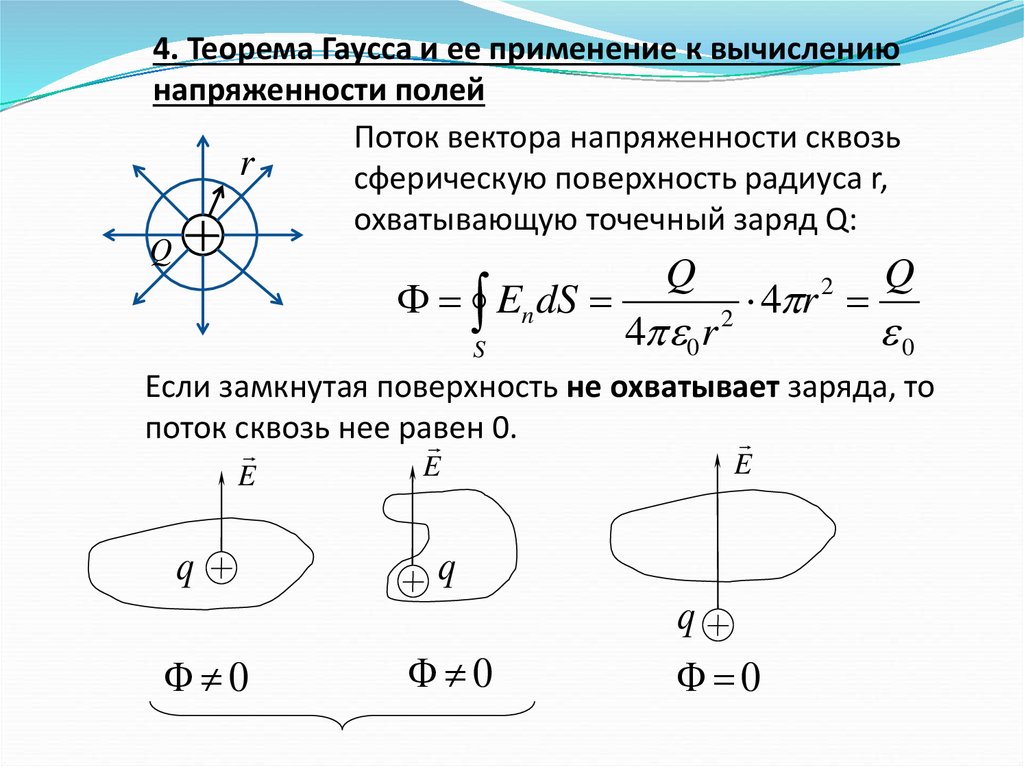
4. Теорема Гаусса и ее применение к вычислениюнапряженности полей
Поток вектора напряженности сквозь
r
сферическую поверхность радиуса r,
охватывающую точечный заряд Q:
Q
En dS
S
Q
4 0 r
4 r
2
2
Q
0
Если замкнутая поверхность не охватывает заряда, то
поток сквозь нее равен
0.
E
q
E
E
q
q
0
0
0
66.
.Пример: Определить поток
вектора напряженности
электростатического поля через сферическую поверхность,
охватывающую точечный заряды
q1 2q
q2 3q
R
2q
3q
2q 3q
0
q
0
67.
Поле образовано зарядами (q1, q2, … qn)n
E E1 E2 ... En Ei
В соответствии с принципом
суперпозиции
электростатических полей:
Поэтому:
i 1
EdS
En dS
S
S
1
0
q
i
i
Теорема Гаусса для электростатического поля в вакууме:
Поток вектора напряженности электрического поля через
произвольную замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности зарядов,
деленной на ε0
Если заряд распределен внутри замкнутой поверхности непрерывно с
объемной плотностью
En dS
S
1
dV
0 V
q
V 0 V
lim
, то теорема Гаусса :
68.
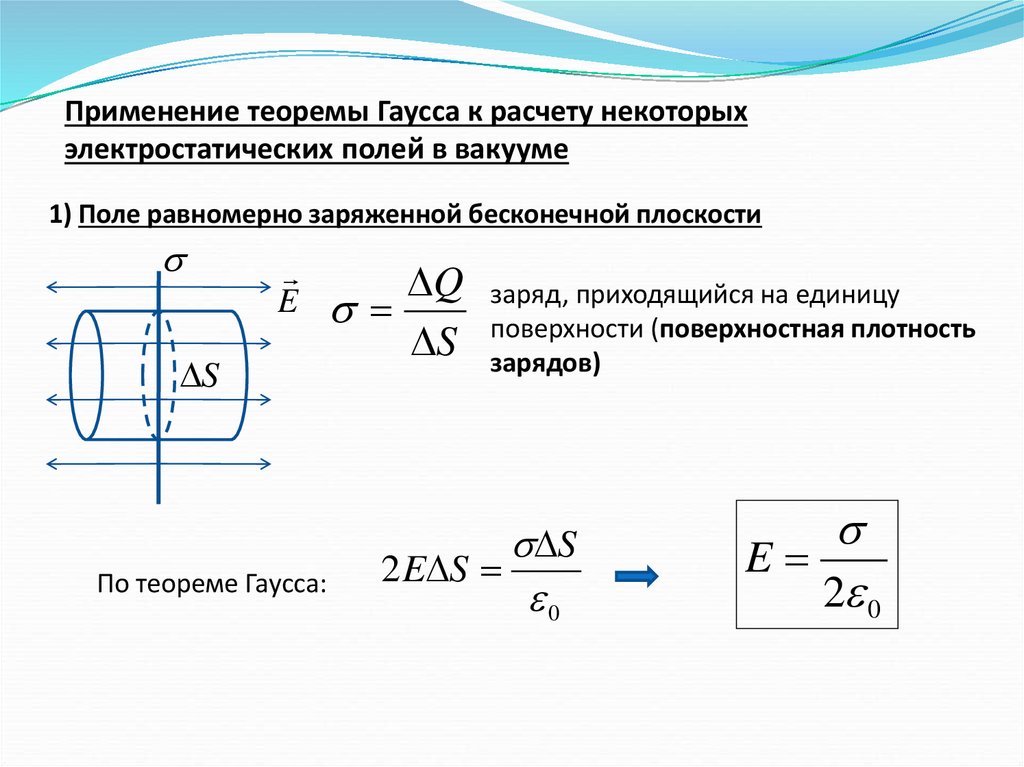
Применение теоремы Гаусса к расчету некоторыхэлектростатических полей в вакууме
1) Поле равномерно заряженной бесконечной плоскости
E
S
По теореме Гаусса:
Q
S
заряд, приходящийся на единицу
поверхности (поверхностная плотность
зарядов)
S
2 E S
0
E
2 0
69.
2) Поле равномерно заряженной сферической поверхности1
Q
E
2
4
r
0
r
R
r
E
E
E
0
E~
R
1
r2
(r R)
E
0
(r R)
E 0
(r R)
гипербола
r
70.
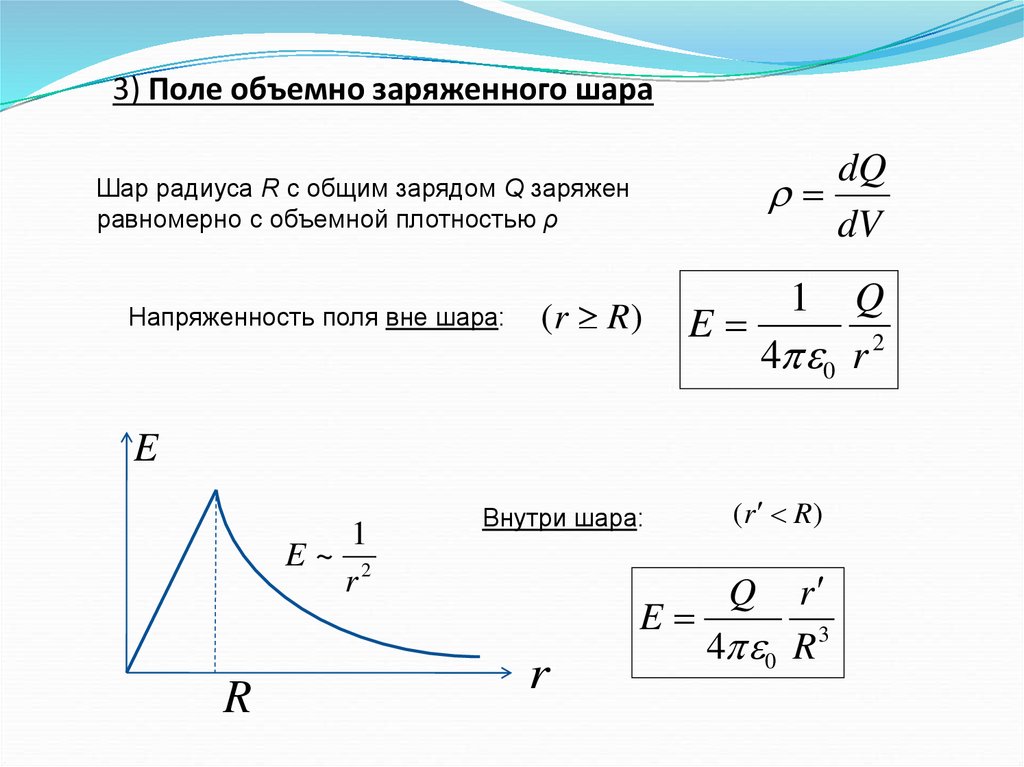
3) Поле объемно заряженного шараdQ
dV
Шар радиуса R с общим зарядом Q заряжен
равномерно с объемной плотностью ρ
Напряженность поля вне шара:
(r R)
1
Q
E
4 0 r 2
E
1
E~ 2
r
R
Внутри шара:
(r R)
r
E
4 0 R 3
Q
r
71.
4) Поле равномерно заряженного бесконечного цилиндраdQ
dl
- линейная плотность зарядов
1
E
2 0 r
E 0
(r R)
(r R)
72.
Потенциал электростатического поля1. Работа сил электростатического поля
2. Потенциал электростатического поля
3. Напряженность как градиент потенциала.
Эквипотенциальные поверхности
4. Вычисление потенциала по напряженности
поля
73.
1. Работа сил электростатического поляВычислим работу, которая совершается силами поля неподвижного
точечного заряда q над перемещающимся зарядом q’.
f
1
Работа на элементарном пути
q'
dl
r
r1
2
dl
1
qq'
1 qq '
dA fdl cos
dl cos
dr
2
2
4 0 r
4 0 r
r2
2
q
qq ' dr
A12
4 0 1 r 2
qq' 1 1
A12
4 0 r1 r2
Работа не зависит от формы траектории, а
определяется только положениями начальной и
конечной точек.
74.
Работа потенциальных сил на замкнутом пути равна 0.Edl El dl 0
A q' El dl
L
L
L
Циркуляция вектора напряженности электростатического поля равна 0.
2. Потенциал электростатического поля
Работу сил электростатического поля можно представить как
разность потенциальных энергий, которыми обладает точечный заряд
q’ в начальной и конечной точках поля заряда q
1
qq'
1 qq'
A12
W p1 W p 2
4 0 r1 4 0 r2
Т.о., потенциальная энергия заряда q’ в поле заряда q:
1
qq'
Wp
4 0 r
75.
Потенциал – энергетическая характеристика поляWp
qпр
1
q
4 0 r
qi
4 0 i ri
1
Работа, совершаемая силами электростатического поля при
перемещении заряда q’ из точки 1 в точку 2:
A12 W p1 W p 2 q' 1 2
Если перемещать заряд q’ из произвольной точки в бесконечность,
где потенциал равен 0, то:
A
q'
B
Дж
В
Кл
Потенциал – физическая величина, определяемая работой по
перемещению единичного положительного заряда при удалении
его из данной точки в бесконечность.
76.
3.Связь между напряженностью электростатическогополя и потенциалом
Работа сил поля над зарядом q на пути dl:
1) А qEl dl
El
l
l
2) А d q q
dl
l
Ex
x
- произвольно выбранное в пространстве направление
E i E x j E y k Ez i
j
k
y
z
x
E grad
Напряженность поля равна градиенту потенциала со
знаком минус. Знак минус определяется тем, что вектор
напряженности направлен в сторону убывания потенциала.
77.
Для графического изображения распределения потенциалапользуются эквипотенциальными поверхностями (геометрическое
место точек с одинаковым потенциалом). Линии напряженности
перпендикулярны эквипотенциальным поверхностям.
4. Вычисление потенциала по напряженности
поля
1) Поле равномерно заряженной бесконечной плоскости:
E
2 0
x2
x2
x1
x1
1 2 Edx
1 2
x2 x1
2 0
dx
2 0
78.
2) Поле равномерно заряженной сферической поверхности радиусаR с зарядом Q:
1
Q
при r R : E
4 0 r 2
Разности потенциалов между точками, лежащими на расстояниях
r1 и r2 от центра сферы, равна:
r2
1 2 Edr
1 2
r1
Потенциал заряженной сферы:
1
~
r
R
r
Q
4 0 R
Q 1 1
4 0 r1 r2

































































 Физика
Физика








