Похожие презентации:
Разностноное уравнение и передаточная функция
1.
Разностноное уравнение и передаточнаяфункция
• Умножив и разделив (7-2) на z2, получим
1 2
1
• H ( z ) 2 ( z a1 z a 2 ) 2 ( z z 01 )( z z 02 )
z
z
• или
(3),
1 2
H ( z ) 2 [ z ( z01 z02 ) z z01 z02 ]
z
• где z01 и z02 – корни квадратного уравнения
• z2 + a1z + a2 = 0.
(4),
2.
Разностноное уравнение и передаточнаяфункция
• Сравнивая (3) и (4), находим, что
z01 z02 a1
z01 z02 a2
(5).
• Комплексно-сопряженные корни
z01 r e
j
,
z02 r e
j
(6).
3.
АЧХ цифрового фильтра• АЧХ нерекурсивного ЦФ
H ( ) (1 a1e
j T
a2 e
2 j T
)(1 a1e
j T
a2 e
2 j T
H ( )
1 a a 2a1 (1 a2 ) cos T 2a2 cos 2 T
2
1
2
2
(11)
)
4.
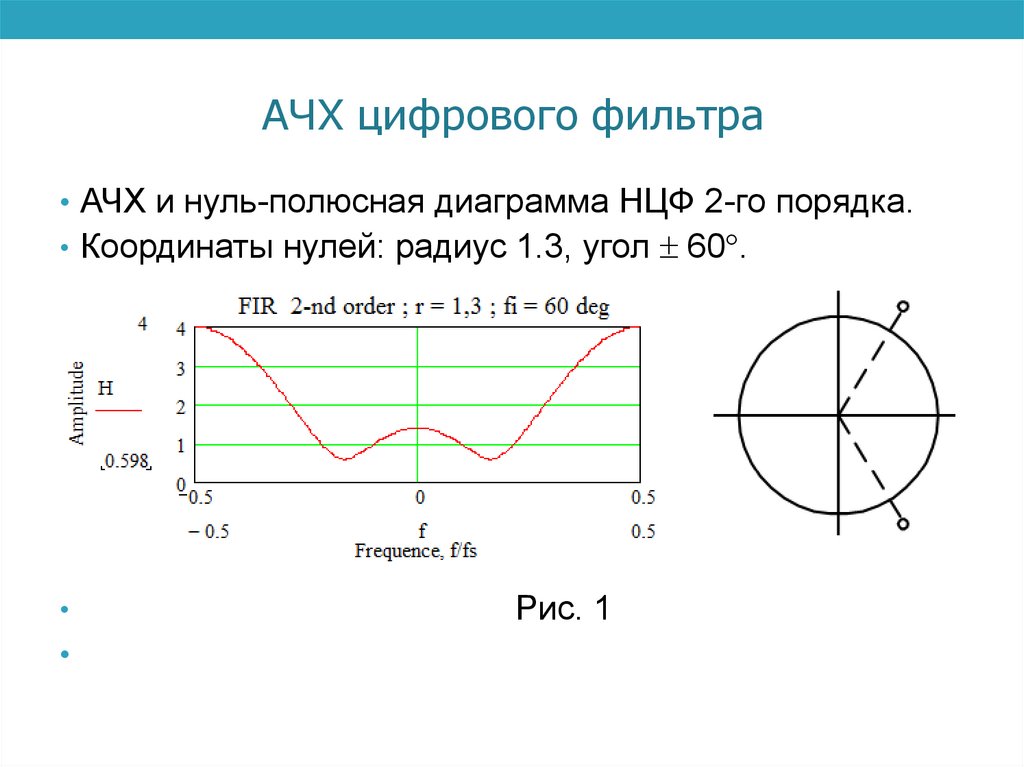
АЧХ цифрового фильтра• АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
• Координаты нулей: радиус 1.3, угол 60 .
Рис. 1
5.
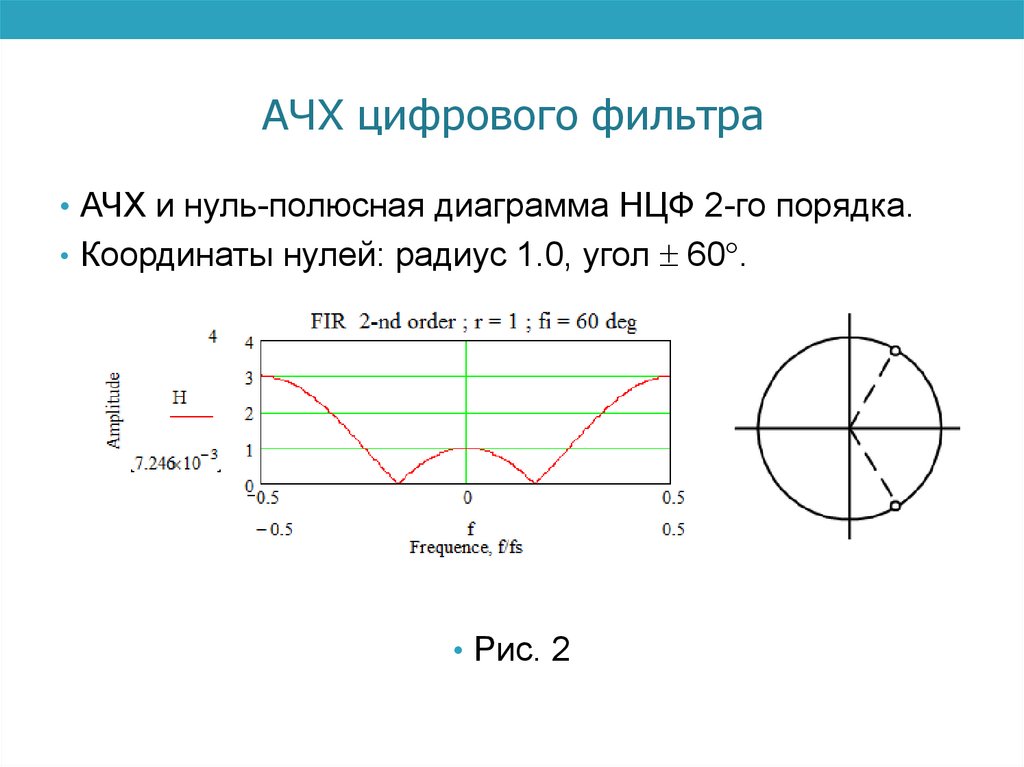
АЧХ цифрового фильтра• АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
• Координаты нулей: радиус 1.0, угол 60 .
• Рис. 2
6.
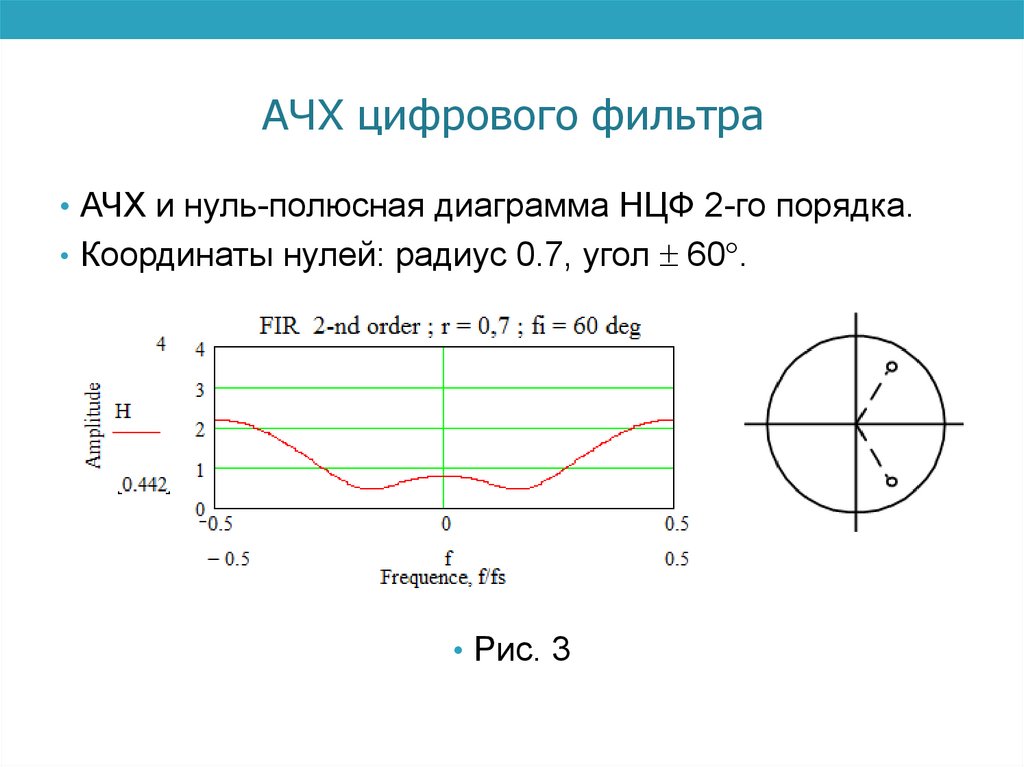
АЧХ цифрового фильтра• АЧХ и нуль-полюсная диаграмма НЦФ 2-го порядка.
• Координаты нулей: радиус 0.7, угол 60 .
• Рис. 3
7.
АЧХ цифрового фильтра• Для того, чтобы получить наибольшее затухание на
частотах вблизи нулей передаточной функции,
необходимо, чтобы нули лежали на единичной
окружности, т.е. должно быть r = 1.
• В этом случае a2 = 1, a1 = -2cos , и АЧХ равна
H ( ) r 1 2 cos T cos
4 sin
T
2
sin
T
2
(12).
8.
АЧХ цифрового фильтра• Если в (3) подставить exp(j T) вместо z и взять
модуль, т.е. вычислить АЧХ, то получим
H ( ) H ( z ) z exp( j T )
1
e
2 j T
e
j T
z01 e
j T
z02
9.
АЧХ цифрового фильтра• Так как модуль комплексной экспоненты равен
единице, а модуль разности между текущей точкой
exp(j T) и положением нуля равен расстоянию между
ними (см. рис 4), то значение АЧХ НЦФ на частоте
равно произведению расстояний 0i от точки ej T,
лежащей на единичной окружности плоскости z, до
всех нулей фильтра:
H ( ) 01 (e
j T
) 02 (e
j T
)
(13).
10.
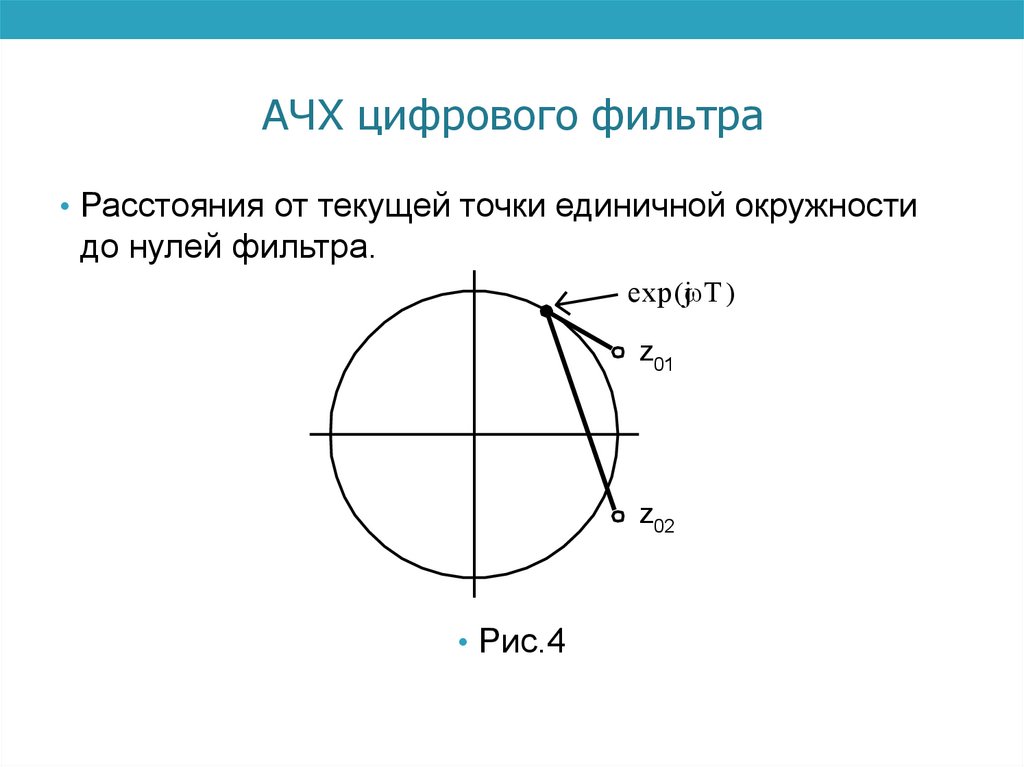
АЧХ цифрового фильтра• Расстояния от текущей точки единичной окружности
до нулей фильтра.
exp(j T )
z01
z02
• Рис.4
11.
АЧХ цифрового фильтра• Так как
N 1
H ( z ) z e j T a n z
N 1
n
n 0
z e j T
N 1
N 1
n 0
n 0
an e
jn T
n 0
an cos(n T ) j an sin( n T )
• то АЧХ НЦФ общего вида.
H ( )
2
a n cos( n T ) a n sin( n T )
n 0
n 0
N 1
N 1
(14)
2
12.
ФЧХ цифрового фильтра• ФЧХ НЦФ
N 1
a
( ) arctg Nn 01
a
n 0
n
sin( n T )
n
cos( n T )
(15)








 Физика
Физика Электроника
Электроника








