Передаточная функция

1.

Передаточная функция
• Рассмотрим рекурсивное звено второго порядка с
разностным уравнением
• yn = xn + a1xn-1 + a2xn-2
b1yn-1 b2yn-2
(1).
• Его передаточная функция имеет вид
1
2
1 a1 z a2 z
H 2 ( z)
1
2
1 b1 z b2 z
(2).

2.

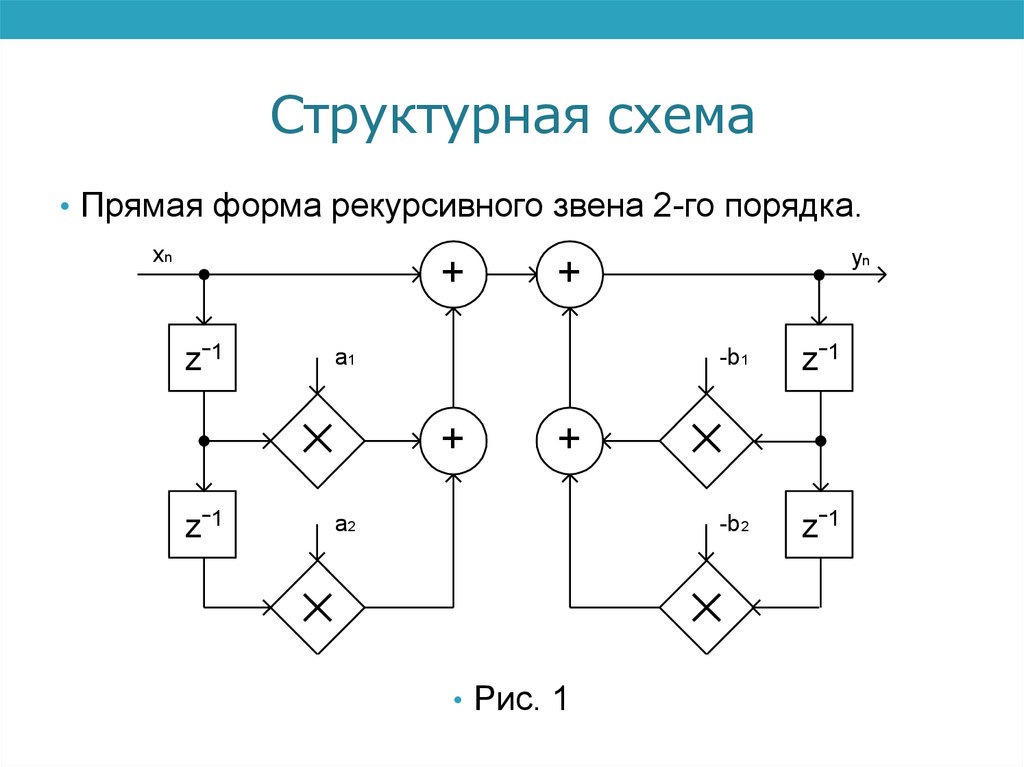
Структурная схема
• Прямая форма рекурсивного звена 2-го порядка.
xn
+
z-1
z-1
+
a1
+
yn
-b 1
z-1
-b 2
z-1
+
a2
• Рис. 1

3.

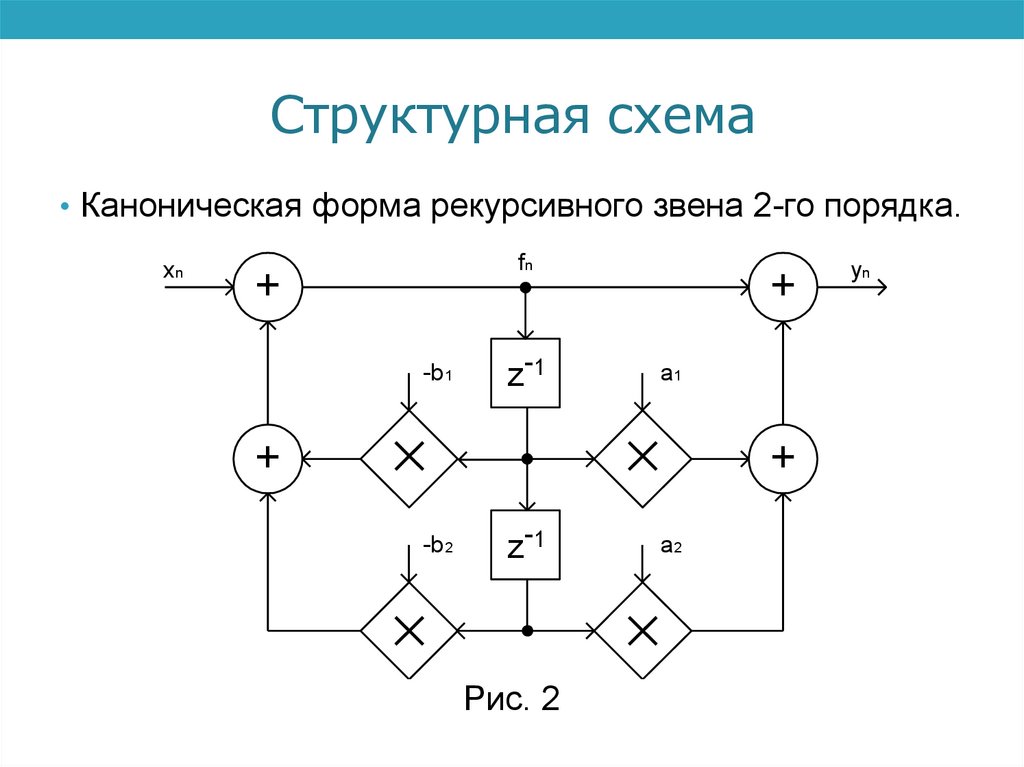
Структурная схема
• Каноническая форма рекурсивного звена 2-го порядка.
xn
fn
+
-b 1
z-1
+
a1
+
+
-b 2
z-1
Рис. 2
a2
yn

4.

Передаточная функция
• Воспользовавшись формулой (10) для АЧХ
нерекурсивного звена 2-го порядка, запишем по
аналогии выражение для АЧХ исследуемого
рекурсивного звена 2-го порядка:
H 2 ( )
1 a a 2a1 (1 a2 ) cos T 2a2 cos 2 T
2
1
2
2
1 b12 b22 2b1 (1 b2 ) cos T 2b2 cos 2 T
• (4)

5.

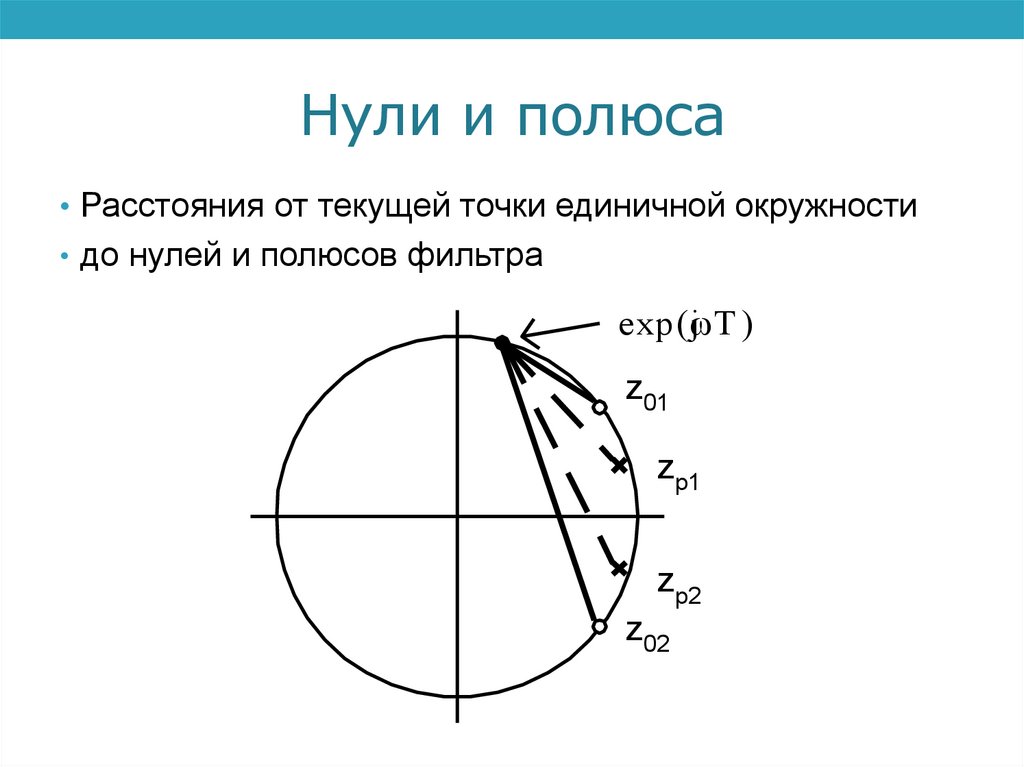
Передаточная функция
• Точно так же, воспользовавшись формулой (12) для
вычисления АЧХ НЦФ 2-го порядка через расстояния
от точки ej T до нулей передаточной функции НЦФ,
запишем по аналогии
• где
01 02
H•2 ( )
p1 p 2
0i – расстояние от точки ej T до i-го нуля
передаточной функции,
• а pi – расстояние от точки ej T до i-го полюса
передаточной функции ЦФ.
(5),

6.

Нули и полюса
• Расстояния от текущей точки единичной окружности
• до нулей и полюсов фильтра
exp(j T )
z01
zp1
zp2
z02