Похожие презентации:
Электромеханические исполнительные элементы и приводы
1.
Министерство образования и науки Российской Федерациифедеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ВОЕНМЕХ» им. Д.Ф. УСТИНОВА
Кафедра Н1
Мехатроника и робототехника
К.т.н., доцент Савельев Б.Н.
Электромеханические
исполнительные элементы и
приводы
Иллюстративный материал
курса лекций
Часть 1
Санкт – Петербург
2015 г.
2.
ВведениеОсновные понятия и определения
1. Механика - наука о механическом движении материальных тел и происходящих при этом
взаимодействиях между телами.
2. Привод
– устройство приведения в движение механических объектов различного назначения.
3. Система автоматического привода (САП)
САП- совокупность устройств, объединенных в систему, предназначенную для приведения в
движение и управления движением рабочих органов машин или иных механических объектов
управления в соответствии с заданной технологией.
4. Электроника
- наука о взаимодействии электронов с электромагнитными полями и о методах
создания приборов и устройств, в которых это взаимодействие используется
для преобразования электромагнитной энергии, в основном, для передачи,
обработки и хранения информации
5. Мехатроника
-область науки о механическом движении, взаимодействии твердых тел и
управлении их движением с использованием электронных приборов и
устройств.
6. Мехатронная система
- система автоматического управления движением механических
объектов, построенная с использованием электронных приборов и
устройств.
3.
Основные понятия и определения7. Техническая система - устройство, которое обладает совокупностью следующих основных признаков:
- является законченным видом технической продукции;
- состоит из взаимодействующих элементов, узлов, агрегатов, подсистем;
- самостоятельно выполняет определенные функции;
- взаимодействует с внешней средой и другими техническими объектами.
8. Управление - процесс целесообразного воздействия на объект управления, обеспечивающий его
желаемое (заданное) поведение, режим работы или выходные переменные.
9. Регулирование - частный случай процесса управления, целью которого является воспроизведение
системой поступающих на нее извне заданий (задающих воздействий).
10. Автоматизация - процесс исключения человека из технологического процесса или из отдельных
его операций (выполнение операций без непосредственного участия человека).
11. Система автоматического управления (САУ)
САУ каким-либо объектом называется техническая система, включающая в себя этот объект
управления(ОУ) и присоединяемую к нему автоматическую аппаратуру, обеспечивающую
заданный режим работы или выходные переменные объекта в соответствии с командами
задающего устройства, являющегося частью этой автоматической аппаратуры.
12. Автоматическая управляющая система -автоматическая аппаратура САУ.
13. Система автоматического регулирования (САР)
САР – техническая система, в которой задаваемый от внешнего задающего устройства режим
работы ОУ или его регулируемая переменная воспроизводится и поддерживается с помощью
присоединяемых к ОУ автоматически действующих устройств.
14. Автоматический регулятор - автоматические устройства САР,
4.
Обобщенные схемы САУ и САРV
U
АУС
АЗУ
ОУ
Авт. рег
Условные обозначения:
Y
Y - регулируемые переменные ОУ;
- возмущающие воздействия на ОУ;
V
U - управляющие воздействия на ОУ;
Рис.1 Обобщенная схема САУ
V
ЗУ
Авт. рег
U
ОУ
Рис.2 Обобщенная схема САР
ОУ – объект управления;
АУС – автоматическая управляющая
система;
Авт. Рег. – автоматический регулятор;
АЗУ – автоматическое задающее
устройство;
Y
- управляющие воздействия на САР;
ЗУ – внешнее задающее устройство.
5.
Классификация САР по реализованному в них принципу управленияСАР, работающие по разомкнутому циклу
(разомкнутые системы)
V
ЗУ
Авт. рег
U
Y
ОУ
Рис. 3 Управление по задающему воздействию
V
ЗУ
const
Авт. рег
U
Y
ОУ
Рис. 4 Управление по возмущающему воздействию
САР, работающие по замкнутому циклу
(замкнутые системы)
V
Авт. рег
ЗУ
U
ОУ
Y
ОС
Рис. 5 Управление по отклонению
САР комбинированного управления
V
ЗУ
Авт. рег
U
ОУ
Y
ОС
Рис. 6 Управление по отклонению и возмущению
6.
ФУНКЦИОНАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО МОМЕНТНОГО ПРИВОДАпри косвенном измерении момента и компенсации противо ЭДС
3 220 v
Г
ИD
ОЯг
Mf Г Г
ПD
E ЯГ
M пд
M ТР Г M Г
IЯ
UЯ
УУ
U Мо
КК
U
ЭУ
BГ
BAD
I BГ
ОВг
MД
DМ
DС
Рис.7
РЕД
I BД
O
MUo
ОУ
MТР Д
Ф BД
U BД
д
E ЯД
КОд
КОг R ш
Ф BГ
U Мз
ОЯд
Mfo
ОВд
Mfд i Р Р
MРo
7.
Классификация САР по наличию УПУ и дополнительного ИПОбобщенные функциональные схемы САР
Авт. рег
ЗУ
ИУ
УПУ
УУ
V
УИ
УПОИ
U
ОУ
Y
ИП
УИ
УПОИ
Рис.8 САР непрямого действия.
V
Авт. рег
ЗУ
УИ
РО
U
ОУ
Y
Условные обозначения:
ИУ – исполнительное устройство;
УПУ – усилительнопреобразовательное устройство;
УУ – устройство управления;
УИ – устройства измерений;
УПОИ – устройства предварительной
обработки информации;
РО – регулирующий орган,
Рис.9 САР прямого действия.
ИП – источник питания
8. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРЯМОГО ДЕЙСТВИЯ
РЕГУЛЯТОР ПОЛЗУНОВАРЕГУЛЯТОР УАТТА
ВОДА
ПАР
ОН
Паровая
турбина
Объект
нагрузки
Масса
Регулирующий
орган
Центробежный
механизм
ДАТЧИК УРОВНЯ
Регулирующий
орган
ПАР
ТОПКА
Рис. 11
Рис. 10
9.
Классификация САР по характеру внутренних процессовСтатические характеристики звеньев непрерывного действия
Рис.11 Пропорциональная
Рис.12 Кусочно - линейная
Рис.14 Зона нечувствительности
Рис.13 Насыщение
И тому подобные
10.
Статические характеристики звеньев дискретного действияРис.15 Статические характеристики звеньев релейного действия
t
t
Рис.16 Статические характеристики звеньев импульсного действия
11.
САР температуры охлаждающей жидкости в двигателеАккумуляторная
батарея
Датчик
Двигатель
вентилятора
Задатчик
0
tC
Термо
Р
а
д
и
а
т
о
р
стат
ДВ
Регулир.
объект
Рис.17
12. Классификация приводов по схеме построения силовой части
Индивидуальный однодвигательныйпривод
Групповой привод
УУ
УУ
УМ
ИП
ИД
ИД
МП
МП
ОУ
Рис.18
ИП
УМ
ОУ2
ОУ1
1
ОУ3
2
Рис.19
3
13.
Индивидуальный многодвигательныйпривод
Дифференциальный привод
УУ
УМ
ИП
ИД
МП
ОУ
Рис.20
УУ
УМ
УМ
ИД
ИД
ИП
УМ
ИД
МД
ОУ
Рис.21
14.
Многокоординатный привод(система приводов)
У У2
У У1
У М1
ИП
У М2
ИД1
ИД2
МП1
МП2
ОУ
Рис.22
2
1
15.
Функциональная схема САПИП
ВАД
УИ
Эл-ты вспомогат.
подсистем
ЗУ
U
му
УУ
ЭУ
ВАД
УИ
УПУ
Информационная часть САП
Рис.23
ИД
МП
ОУ
О
Энергетическая часть САП
Условные обозначения:
ИД – исполнительный двигатель;
УПУ – усилительно-преобразовательное устройство;
ЭУ – электронный усилитель;
УУ – устройство управления;
ОУ – объект управления;
МП – механическая передача;
УИ – устройства измерений;
ВАД– вторичная аппаратура датчиков;
16.
Основные воздействия на ДПТ НВ, выходная переменная и режим работыMэм
IЯ
E ЯД ОЯ
UЯ
MТР M f
ОДП КО
Ф
UB
IB
ОВ
Рис.24 Принципиальная схема ДПТ НВ
Условные обозначения на схеме:
ОЯ – обмотка якоря ДПТ;
ОВ – обмотка возбуждения ДПТ;
КО – компенсационная обмотка ;
ОДП – обмотка дополнительных полюсов ;
Uя t , Uв t - напряжения на зажимах цепи якоря и цепи
возбуждения машины ;
Iя t , Iв t - токи в цепи якоря и цепи возбуждения ДПТ ;
E я t - ЭДС якоря машины ;
М эм t - электромагнитный момент на валу двигателя;
М тр t - момент трения на валу двигателя;
М f t - внешний возмущающий момент на валу ДПТ.
t - скорость вращения вала ДПТ;
Ф t - поток цепи возбуждения электромашины;
Управляющие воздействия на ДПТ НВ
При управлении по цепи якоря:
U я t
При управлении по цепи возбуждения:
или
Iя t
Uв t
или Iв
t
Возмущающие воздействия
М f t - внешний момент нагрузки на валу двигателя.
Выходная переменная
t - скорость вращения вала двигателя.
Режим работы двигателя постоянного тока независимого возбуждения.
{U я t , Uв t , M f t } - совокупность (вектор) существенных воздействий:
При UЯ const , UВ const , M f const - режим статический.
17.
Уравнение движения электродвигателя постоянного токаПринимаемые допущения:
- параметры машины на рассматриваемом интервале времени не изменяются;
- реакция якоря полностью скомпенсирована компенсационной обмоткой ДПТ;
- гистерезисом магнитной цепи машины пренебрегаем;
- кривая намагничивания аппроксимирована кусочно-линейной характеристикой “насыщение”;
- трения на валу машины хорошо описываются характеристикой «сухое трение».
Уравнения равновесия ЭДС в цепях электромашины
В цепи якоря:
d I я t
t
t
t
t
t
E я t
Uя
U Rя
U Lя
Eя
R я Iя
Lя
dt
В цепи возбуждения:
Uв t U Rв U Lв R в Iв t Lв
d Iв t
, где
dt
(1)
(2)
Uя t , Uв t - напряжения на зажимах цепи якоря и цепи возбуждения машины ;
URя t , ULя t - падение напряжения на активном и реактивном сопротивлении якоря;
URв t ; ULв t - падение напряжения на активном и реактивном сопротивлении ОВ;
Iя t , Iв t - токи в цепи якоря и цепи возбуждения машины ;
E я t
R я,Rв
L я , Lв
- ЭДС якоря машины ;
- активные сопротивления цепи якоря и цепи возбуждения машины ;
- индуктивности цепи якоря и цепи возбуждения машины .
E я t cе Ф t t , где
Ф t - поток цепи возбуждения электромашины;
t - скорость вращения вала ДПТ;
cе - конструктивная константа электромашины.
(3)
18.
Уравнение магнитной цепи электродвигателяФ
Ф t
Фнас
-Iв нас
Iв нас
Iв
-Фнас
Iв t
при
Iв t Iв нас
Фнас Sign Iв t при Iв t Iв нас
(4)
Фнас - поток насыщения магнитной цепи ДПТ;
Iв нас - ток возбуждения насыщения магнитной цепи ДПТ;
- тангенс угла наклона линейного участка кривой.
Рис.25 Кривая намагничивания магнитной цепи ДПТ при принятых допущениях
Уравнение моментов на валу электродвигателя
М эм t М f t М тр t М дин t 0, где
(5)
М эм t - электромагнитный момент на валу двигателя;
М f t - внешний возмущающий момент на валу двигателя;
М тр t - момент трения на валу двигателя;
Мдин t - динамический момент вала двигателя.
М эм t См Ф t Iя t ,
М тр
(6)
См - конструктивная константа ДПТ НВ,
Мтрс
д
-Мтрс
Мдин t J д t J д
d t
,
dt
(7)
J д - момент инерции подвижных частей двигателя;
t - угловое ускорение вала двигателя.
Рис.26 Характеристика сухих трений на валу двигателя.
при 0
М трс t Sign
М тр t Мэм t М f t при 0 и Мэм t М f t Мтрс
Мтрс Sign (Мэм t М f t ) при 0 и Мэм t М f t Мтрс
(8)
19.
Уравнение движения электродвигателя постоянного токаРешая систему уравнений (1) – (8) относительно скорости, получим уравнение движения ДПТ,
связывающее выходную переменную двигателя с основными воздействиями на него.
d
Jд Lя
Jд R я
d2
2
2
2
dt
Се См Ф Uв d t
Се См Ф U я
Rя
Lя d )
Uя
Rя
Lя d )
(
1
(
1
Mf
M
тр
Се См Ф2 Uя
Се Ф Uв Се См Ф2 U я
R я dt
R я dt
(9)
В статических режимах работы двигателя воздействия на него и выходная переменная
имеют постоянные значения. Следовательно производные от них будут равны нулю, и
уравнение примет вид:
Uя
Rя
Rя
Uя
Rя
Mf
M
Mэм
тр
2
2
2
Ф
Ф
С
С
U
Се Uв Се См Ф Uя
Се Uв Се См Ф Uя
е мФ
я
(10)
Его называют уравнением статических характеристик ДПТ НВ
Статические характеристики ДПТ НВ
Механические характеристики
f ( Mд )
Uя const
Uв const
M д М f - полезный момент на валу двигателя.
Регулировочные характеристики
Регулировочные при управлении по цепи якоря
f ( Uя )
M f const
Uв const
Электромеханические (скоростные) характеристики Регулировочная при управлении по цепи возбуждения
f (I Я )
Uя const
Uв const
f ( Uв )
M f const
Uя const
20.
Семейство статических механических характеристик идеализированного ДПТ НВ(при отсутствии трений на валу)
Уравнение механических характеристик для этого случая:
Искусственные при
R доб1 R доб2 R доб3
R доб1
R доб 0
U я R я 2 Mэм 0 1 Мэм
ст
се Ф се см Ф
0
R доб2 R доб3
Uя
се Ф
Мкз
Искусственные
при U я
Uян
о3
скорость идеального
холостого хода
Uя Ф
се
Rя
момент короткого
замыкания
2
сс
ст е м Ф
Rя
он
статический модуль
жесткости хар-ки
f (Mэм) Uя Uян
Н
Ф(U в) Фн ( Uвн)
о1
-естественная хар-ка
о2
- М кзн
- М кз1
- М кз2
-МЭМН
МЭМН М кз2
о2
о1
Н
он
М кз1
М кз3М кзн
Ф3
Мэм
Ф1
Ф2
Ф Фном
Ф1 Фном
Искусственные при
Рис.27
Ф3
Ф2
21.
Семейство статических механических характеристик ДПТ НВпри учете сухих трений в подвижных частях машины
Уравнение статических механических характеристик:
Искусственные при Ф
Искусственные при R доб 0
Фном
0ф
Искусственные
при U я
Uян
ххн
он
хх1
хх2
- М кзн
- М кз1
1
U я R я 2 M трс R я 2 Mд хх
Мд
ст
Се Ф Се См Ф
Се См Ф
Uя R я
хх
Mтрс - скорость
Се Ф Се См Ф2
холостого хода
тр R я 2 Mтрс - просадка скорости,
вызванная трениями
Се См Ф
2
с
е см Ф
статический модуль
ст
Rя
жесткости хар-ки
- М кз2
01
02
хх2
хх1
он
Рис.28
ххн
М ТРс
М кз2
М кз1 Мкзф М кзн
М ТРс
Мд
22.
Регулировочные характеристики ДПТ НВ при управлении по цепи якоряУравнение статических характеристик ДПТ НВ:
Уравнение регулировочной характеристики:
2б
2а
1
1
U я R я 2 M трс R я 2 Mд хх
Мд
ст
Се Ф Се См Ф
Се См Ф
f (Uя) M const
f
Uв const
Рассмотрим характеристики при различных
значениях фиксируемых переменных.
4
1
3
5
2
3
Uя (0)
Uя
се Ф н
M f М и 0 ; | Ф | const Фн
U
2а 0 Ф Фн
я
2б 0 Ф - Фн
см Ф
M f M fo const 0; Ф Фн
M f М и 0 ; Ф Фн
Uя R я 2 M fо
Се Фн Се См Фн
Uя
U(0) R я M f
се Ф
кз
кз
Rя
2 M fо
се см Фн
M f Mтрc Sign ; Ф const Фн
Uя R я 2 Mтрс Sign
Се Фн Се См Фн
5 M f M fo M трс Sign ; Ф Фн
4
4
5
Рис.29
Uя R я 2 Mтрс Sign R я 2 M fo
Се Фн Се См Фн
Се См Фн
23.
Регулировочные характеристики ДПТ НВ при управлении по цепи возбужденияУравнение статических характеристик ДПТ НВ:
f ( Uв )
Уравнение регулировочных
характеристик:
Uя соnst
M f соnst
3а
U В ( 0) U В э
3а
А
ихх
3.
н
UВНАС
3
2
1
А
Рис.30
U Ян
се Ф UВ
UЯ
се Ф UВ
Б
ИХХ
UЯн
се Фнас
Б
ИХХ
UЯ
се Фнас
UЯ UЯн ; MЭМ соnst MЭМн
U Ян -1 R Я М эмн -2
А
2 -2 U В
-1 U в
cе R В
cе c м R В
Uв
А
d
UЯн
R Я Мэмн -3 0
-2
2
U
в
2 - 2 UВ
-1
d UВ
cе R В
cе cм R В
2
R
U
Я М эмн
Ян
U Вэ 2
э
U Ян cм R В
4МЭМн R Я
R Я М эмн
UЯ R Я МЭМн
Б
;
UВ 0
2
U Ян cм R В
се Фнас се см Фнас
э
Б
MЭМ соnst 0
UЯ UЯн ; MЭМ соnst 0
2.
4 3
UВНАС - Uвэ
UЯ UЯн ;
1.
А
2
Мэм Мтр М f
Рассмотрим характеристики при различных
значениях фиксируемых воздействий
1
э
ихх
Uя R я 2 Мэм ;
Се Ф Се См Ф
Б
3а.
4.
UЯ UЯн ; MЭМ соnst MЭМн
UЯ UЯн ; MЭМ МТРc Sign
24.
Режимы работы двигателя и область допустимых режимов работыРежимы работы по направлению потока энергии на выходе двигателя подразделяют:
Тормозные режимы:
Sign Sign M в
1. Двигательные
2.1 торможение противовключением Sign
Sign Sign M в
2. Тормозные
3. Холостого хода
4. Короткого замыкания
2.2 торможение рекуперативное
M в 0 ; хх
0 ; М в М кз
2.3 торможение динамическое
Область допустимых режимов
Границы области по моменту:
При наличии
IЯ IЯm и МЭМ МЭМm cM Ф IЯm ,
II
где
IЯm
- максимально допустимое значение тока якоря двигателя.
Момент на валу ДПТ:
РТ
ххн
ТПВ
хх1
хх2
- М кзн
- М кз1-МЭМm - М кз2
он
I
- в двигательных режимах
- в тормозных режимах
Дв
Естественные характеристики при
UЯ UЯн ;
UВ UВн ;
М ТРс
М ТРс
хх2
М кз2 МЭМm М кз1
М кзн
Мв
хх1
он
ТПВ
ххн
Дв
III
РТ
Рис.31
Мв МЭМm Мтр
Мв МЭМm Мтр
Границы области по скорости:
01
02
Sign хх
Sign Sign хх
хх 0
IV
25.
Статические характеристики мощности электродвигателейЭлектромашины являются преобразователями энергии электрической в механическую или наоборот.
Статическими характеристиками мощности называют зависимости мощности на входе или выходе электромашины
от одной из обобщенных сопряженных координат этой мощности в определенном режиме использования.
Статические характеристики мощности на входе и выходе электродвигателя
Nэ U я I я
Под входной мощностью ДПТ НВ понимается электрическая мощность на зажимах якоря машины
Под выходной мощностью электродвигателя понимается механическая мощность на валу машины
Nм Мв
М
эм
Так как ток якорной цепи определяется выражением: Iя
, а Мэм М f М тр ,мощности на входе
N э f ( U я , М f , Uв )
и
Nм f ( U я , М f , Uв )
см Ф
на выходе ДПТ являются функциями режима его работы.
Рассмотрим вид этих характеристик в основных режимах использования двигателя, а именно:
При работе на одной механической характеристике (управляющие воздействия постоянны);
1.
2. При регулировании скорости вращения вала изменением U я при постоянном моменте Мэм М f const ,
3. При стабилизации скорости вращения вала изменением U я при изменении момента Мэм М f var,
Уравнениями характеристик мощности в 1 -ом режиме использования являются:
Nэ f (Iя) Uя const
Uв const
Nм f ( ) Uя const
Uв const
Уравнениями характеристик мощности во
Nэ f ( Uя) M f const
Uв const
В
или
Nм f (Мэм (Мв)) Uя const
Uв const
2 -ом режиме использования являются:
N м f ( ) М f const
Uв const
3 -ем режиме использования изменяются и U я , и Iя f (Мэм), поэтому характеристиками являются:
N м f ( М и ( М в )) const
Nэ f ( Uя) const и Nэ f (Iя ) const
Uв const
Uв const
Uв const
Характеристики могут быть сняты экспериментально или построены теоретически при использовании модели ДПТ.
При принятых ранее допущениях ДПТ НВ в статических режимах работы описывается уравнениями:
Uя R я 2 Mэм 0 1 Мэм
ст
се Ф се см Ф
или
1
Uя R я 2 Mтрс R я 2 Mв хх
Мв
Ф
Се
Се См Ф
Се См Ф
ст
26.
1.1 Характеристики мощности на входе ДПТ НВ при постоянных управляющих воздействиях(при работе на одной механической характеристике)
Уравнение характеристики электрической мощности
Nэ
тпв
Nэ3
Nэкз
Nэ1
дт
I я4
Nэн
Nэи
ихх
РТ
дт
н
1
Nэ4 2
Iкз I я3
Iя
- мощность на зажимах якоря ДПТ НВ
в номинальном режиме
2. При работе на искусственной механической характеристике
Uя
Uян ; Uв Uвн ;
Iя Iян Nэи Uя Iян
Выделим на характеристике мощности режимы работы ГД
Отобразим рабочие точки механической характеристики на характеристике
мощности, а мощность на зажимах якоря Nэ на плоскости механических
характеристик
Мэм
4
Nэ U я Iя о се Ф
ое
N э1
см Ф
о Мэм
Сравнивая построения на Рис.32 и Рис.33, установим следующее:
При Iя 0 (Мэм 0) - идеальный холостой ход ГД.
(1)
Nэ2
N экз
При
Nэ3
(2)
М эм4
3 0МэмнМэм1 Мэм2
Рис.33
Nэ Iя »
Nэн Uян Iян
При
Рис.32
(4)
Iя
1. При работе на естественной механической характеристике
дт
- Nэ4
(4)
линейное от
Uян R я 2 Mэм Построим ее на плоскости« - Мэм»
Се Фн Се См Фн
2
Uян ;
Uян
Характерные точки: Мэмкз Iякз см Фн
см Фн ; ое
с м Фн
Rя
,
;
ном.
режим.
При I я I ян М эм М эмн см Фн I ян
(1)
0 Iян Iя1 Iя2
Uя const
Уравнение естественной характеристики ДПТ НВ имеет вид:
(2)
дв
при
Построим характеристики мощности на плоскости «
1
(3)
кз
Nэ2
N э U я Iя
При
Мэмкз М эм3 М эм
(3)
дт
Iя Iякз (Мэм Мэмкз)- режим короткого замыкания.
0 Iя (Мэм) Iякз (Мэмкз) - двигательные режимы.
При I я I якз (Мэм Мэмкз)- режимы торможения
противовключением ТПВ
режимы
торможения
При Iя 0 (Мэм 0)
При
Uя 0
рекуперативного РТ.
- режим динамического торможения ДТ
27.
1.2 Характеристики мощности на выходе ДПТ при постоянных управляющих воздействиях(при работе на одной механической характеристике)
Уравнение характеристик механической мощности на валу
Т.к.
f (Mв (Мэм))
Nм
1
Uян R я
Mэм о
Мэм
или
ст
Се Фн Се См Фн2
Умножая выражение для момента на , а выражение для скорости наМ эм,
Nм
М и ( о ) ст
0.75N экз
получим уравнения характеристик механической мощности:
-1
N м ( о 2 ) ст
Nм 0 Мэм - ст М2эм ;
Это параболы, найдем координаты точки экстремума: -1
Nвх
N пот
дв
0.25N экз
0.25N экз1
N м ( о 2 ) ст 0
N мэ
N мн
э 0.5 о
М эм М эмкз N п
0 ихх
Микз/2
кз 0 о1 хх о о1 н хх о
Мв
Nр
2 2 2
N вых
N
тпв
3
U я const , Uв const.
N м f и Nм f (Мв(Мэм)).
при
могут быть построены два вида характеристик:
1. Характеристики на выходе ДПТ без учета механических потерь
Уравнение механической характеристики
N экз
0.5N экз
Nм Мв
ДТ
Рис.34
РТ
N м о 2 Мэм ст 0
Мэмэ 0.5 о ст 0.5
Uя cм Ф 0.5
Мэмкз
Lя
Nмэ 0.25 о2 ст 0.25 о Мэмкз 0.25 U я Iякз 0.25 Nэкз
Rя
о
0
Точки пересечения с осью абсцисс (Nм=0)
- режим ИХХ
М 0 - режим ИХХ
эм
Мэм о ст Мэмкз - режим КЗ
Нанесем эти точки на плоскости « N м » или « Nм М эм» и построим характеристики
2
4 N мех
1
- режим КЗ
2. При работе на искусственной механической характеристике
Экстремум э 0.5 о1
Nмэ1 0.25 Nэкз1 Мэмэ 0.5 Мэмкз1
о
хх
3. Вторая характеристика может быть построена самостоятельно или совмещено
Режимы работы ДПТ: 0 о дв., 0 тпв., о рт. о 0 ; 0 дт.
4. Характеристики на выходе ДПТ при учете механических потерь
хх ст-1 М в
М в ( хх ) ст
о1
0
Рис.35
Микз1М вкзМ екз
М эм
Экстремум э
0.5 хх N мэ 0.25 хх М вкз М вэ 0.5 М вкз
28.
2.1 Характеристики мощности на входе ДПТ НВ при регулировании скорости вращения вала(управляющее воздействие расход на штуцерах Qш)
Уравнение характеристики мощности
Nэ Uя , Iя(М f ), )
f(
Nэ
3
N эн
(5)
2.1.1.Характеристики на входе ГД без учета механических потерь
Nэ11
(2)
кз
U я5 U я4 Q трсДТ 0 UUтрсU я2 U я3 U ян
я1
РТ
(4)
Nэ14
Рис.36
2
4
1
о 3
Nэ13
о 2
(3)
о 1
-М трс
(5)
4
1
о 4
дт
о5
4
0
Nэ12
Nэ11
(2)
Мэм2 М трс М эм1
(1)
Nэ14
(0)
(4)
Рис.37
Рассмотрим их при различных значениях фиксируемых параметров:
Мэм1 Мэмн М f const; Uв Uвн .
Уравнение характеристики: N э1 I ян U я I я I ян М эмн см Ф
2
При U я U ян ; N эн U ян I ян - мощность на входе ДПТ в
номинальном режиме
Uв Uвн .
2. Мэм2 Мэмн Мв const ;
Уравнение характеристики: N э2 U я I2
При U я U ян ; N э2 U ян I я2 N ян
Uя
3. Мэм3 Мэмн Мв const ; Uв Uвн .
Мэмн
Уравнение характеристики: N я U я I я3
Iя3
Iян
Ф
с
U
м
в3
4. Мэм4 Мв М трс Sign ; U вн .
Уравнение характеристики: N э U я I я4
(cеФ) 1 Sign при Uя Uтрс R я (сеФ) 1 Мтрс ( 0)
U
М
трс
я
1
NЭ4
Uя Iякз U2я R -я1 при Uя Uтрс R я (смФ) Мтрс ( 0)
4
(3)
тпв
(1)
Построим характеристики мощности на плоскости « Nэ U я »
1
ДВ
Nэ13
N эн
Nэ12
Uя Iя
1.
Режимы работы ДПТ на характеристике мощности
Отобразим их на плоскости« Мэм» и характеристике мощности.
Uя 0 ( о 0) рабочая точка (0) – режим ДТ;
1
0
Ф
U
U
М
R я рабочие точки (1) - режим ТПВ;
с
эм
я
якз
м
М эм
1
U я Мэм смФ R я ; ( о2 ; 0) рабочая точка (2) – режим КЗ;
1
U я U якз Мэм смФ R я ( о3) рабочие точки (3) – режим ДВ;
рабочие точки (4) – режим РТ;
Uя 0 (- о4)
29.
2.2 Характеристики мощности на выходе двигателя при регулировании скорости вращения валаNэ
N эн
(управление по цепи якоря)
2.2.1.Характеристики на выходе ДПТ без учета механических потерь
1
Nм
1. Мэм1 Мэмн М f Мв const;
3
Nэ
N мн
ДВ
1 Уравнение характеристики: при
2
N мн
N экз
N м13
0 тпв U якз
4 дт 1 кз 0
РТ
ДТ
РТ
тпв N м11
U ян
U я3
ХХ
н
3
N мдт
N э14
N М4
2
4
1
о 3
ДВ
о 2
о 1
(5)
4
М трс Sign при ( 0)
0 при ( 0)
Рис.38
М трс
н ; Nмн Мэмн н - мощность на валу ДПТ в
номинальном режиме
Uв Uвн .
2. Мэм2 Мэмн Мв const ;
Уравнение характеристики: Nм2 Мэм2
При н ; Nм2 М эм н Nмн
Uв Uвн .
3. Мэм3 Мэмн Мв const ;
Uя
Уравнение характеристики: Nм3 МэмН
4. Мэм4 Мв Мтрс Sign ; U 1.
При
4
ДВ
М эм М эмн
Uвн .
Nм1 Мэмн
(3)
N м13
(2)
Режимы работы ГД на характеристике мощности
0 рабочая точка (2) – режим КЗ;
рабочие точки (3) – режим ДВ;
0
0 дт
дт
дт
рабочие точки (1) - режим ТПВ;
рабочая точка (0) – режим ДТ;
рабочие точки (4) – режим РТ;
Мэм2 М трс М эм1
0
М эм
1 N м11
Потери мощности (мощность потерь в якоре)
N мдт (1) тпв
о 4
Отобразим на плоскости « N м - » характеристики Nэ f ( U я)
(0)
дт
N м14
При Uя 0 Nэ 0 режим ДТ, – начало координат « N э U я »
4
Рис.39
(4)
РТ
Мощность потерь (в якоре)
Nэ Nэн Nмн Nэкз
30.
3.1 Характеристики мощности на входе ДПТ при стабилизации скорости вращения вала(управление по цепи якоря)
Уравнения характеристик мощности Nэ
Uя) или Nэ f (Iя); ( const)
3.1.1.Характеристики на входе ДПТ без учета механических потерь
Уравнение для цепи якоря ДПТ НВ
f(
Nэ
Iя (Uя Eя) R -я1 или Uя Ея Uя се Ф R я Iя
Подставляя выражения для I я и U я в уравнение мощности N э I я U я,
(4)
N э4
1
(1)
N э1
тпв
получим уравнения характеристик мощности на входе ДПТ:
ДВ
(3)
0.5 Е я2 Е я2
Uя4 0 ДТ
Nээ2
- N э2(2)
1
сеФ 1 2 R -я1
4
Е я1 Uя1 U я
1. Построим характеристику
2. Построим характеристику
(2)
1
о 4
Рис.41
(1)
(0)
Nэ1
- N э2 о 2
N э4-М эм2
Nэ f ( U я)
N я f ( Uя)
0
М эм1
3. Построим характеристику
при 1 const и Uвн
при 2 1 и Uвн
Nээ 0.25 сеФ 2 R -я1
Nя f (Uя) при 3 0 ; Ея 0
Характерные точки: Ея2 се Ф 2 ; Uяэ 0.5 Ея 2 ;
о 1
М эм4 М эм3
Uяэ 0.5 Ея 0.5 се Ф Iяэ 0.5 Eя R-я1 0.5 се Ф R-я1
2
Nээ 0,25 E2я R -я1 0.25 сеФ R -я1
я
(3)
N э Eя 2 Iя R я 0
Точки пересечения с осью NЭ = 0:
Iя 0 - режим ИХХ
U я E я режим ИХХ
Iя -Ея R -я1 се Ф R -я1- режим ДТ
U 0 - режим ДТ
РТ
Рис.40
(4)
N э (2 Uя Eя) R -я1 0
2
Точки экстремума:
ИХХ (0)
Uя2 0.5Е я1
Nэ E я Iя Iя R я
Определим характерные точки этих кривых (парабол)
2
3
Nэ (U2я Eя Uя) R -я1
2
Режимы работы ДПТ на характеристике мощности
Отобразим режим стабилизации скорости на плоскости « Мэм»
Мэм 0 - режим ИХХ,
М эм Мэм 0 (Мэм1) - режимы ДВ,
0 Мэм Мэмдт (- Мэм2) - режимы РТ,
Мэм Мэмдт -Мэм3 - режим ДТ,
Мэм Мэм3 (- Мэм4) - режимы ТПВ,
31.
3.2 Характеристики мощности на выходе ДПТ при стабилизации скорости вращения вала(управление по цепи якоря)
Уравнения характеристики мощности:
Nм f (М эм (Мв)); ( const)
3.2.1.Характеристики на входе ДПТ без учета механических потерь
Уравнение характеристики при const Nм М эм линейное.
1. Построим характеристику Nм f (Мэм) при 1 const и Uвн
При Мэм Мэмн ; 1 const Nм1 1 М эмн
1
2. Построим характеристику Nм f (М эм) при 2 1 и Uвн
N э1
(1)
3
N мн
При Мэм Мэмн ; 2 const Nм2 2 Мэмн
Nэ
2 3. Построим характеристику N f (М ) при
N м1
1 const и Uв < Uвн
Nэ (1)
эм
м
ДВ
N мн
Nм
4 4. Построим характеристику Nм f (М эм) при 4 0 и Uвн
ИХХ (0)
М эм2 0
При 0 N м4 0
МэмнМ
Мэм1
эм
Nм
М и4 Мэмдт
- N э2
РТ
ДТ
(3)
тпв
(4)
(4)
(3)
- N м4
Мэм4 Мэм3
(2)
о 1
- N м3 1
- N м 2 о 2
-Мэм2
Режимы работы двигателя на характеристике мощности
- N м2
(2)
- N мдт
- N м4
Рис.42
(0)
(1)
о 4 0
N м1
М эм1
Рис.43
Мэм 0 точка (0) - режим ИХХ,
М эм 0 (М эм1) точка (1) - режимы ДВ,
0 Мэм Мэмдт (- Мэм2) точка (2) - режимы РТ,
Мэм Мэмдт -Мэм3 точка (3) - режим ДТ,
М эм М эм3 (- М эм4) точка (4) - режимы ТПВ,
Потери мощности (мощность потерь в якоре)
Отобразим на плоскости «Nм - Мэм » характеристику N э f ( U я)
Это парабола, пересекающая ось Nэ = 0 в режимах ИХХ и ДТ
Мэм
Мощность потерь
Nэ Nэ Nм
32. Нелинейная математическая модель ДПТ (при принятых ранее допущениях):
ДИНАМИЧЕСКИЕ МОДЕЛИ И ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДПТ НВНелинейная математическая модель ДПТ (при принятых ранее допущениях):
d
U я Е я U R U L с е Ф R я I я L я I я
dt
d
Uв U Rв U Lв R в Iв Lв Iв
Уравнение цепи возбуждения:
dt
Iв при Iв Iвнас
Уравнение магнитной цепи :
Фв
Фнас Sign Iв при Iв Iвнас
d
М эм М f М трс М дин ; см Ф Iя М f М трс Sign J д
Уравнение моментов:
dt
Уравнение цепи якоря:
М эм см Ф Iя
М трс
- электромагнитный момент ДПТ;
Мтрс Sign
при 0
d
М дин J д J д - динамический момент ДПТ;
dt
(Мэм - М f ) при 0 и Мэм М f М трс
- момент сухих трений на валу ДПТ;
М трс Sign (Мэм - М f ) при 0 и Мэм М f М трс
Нелинейная структурная схема ДПТ НВ
UL
Uя
Lя D
UR
МТРс
Iя
1
см
Rя
Ея
URв
Uв
ULв
1
Rв
Iв
М эм
Фнас
Iвнас
Ф
Lя D
Мf
се
Рис.44
М дин
1
JД D
33.
Линеаризация математических моделей звеньевРассмотрим для примера звено с двумя входными воздействиями Х1 и Х2 и одной выходной
величиной Y, динамическое уравнение которого имеет вид нелинейного дифференциального
уравнения:
1
( х1, х 1, х 1,... х2, х 2, х 2,... y, у , у ...) 0
(1)
х
y
х2 х1, х2
Будам считать, что динамический процесс в системе протекает в окрестности некоторой точки
установившегося статического
режима, в которой переменные звена имеют постоянные
о
о
о
значения
Эту точку называют точкой линеаризации.
1
2
о
о
о
(11)
Уравнение звена в этом режиме:
х ;х ; у .
( х1 , 0, 0,... х2, 0, 0,... у ,0,0...) 0,
а переменные в динамическом режиме можно представить:
х1 t х1о х1 t ;
о
t
х2
х2 х2 t ;
у t у о у t ;
х 1 t х 1 t ;
х 2 t х 2 t ;
у t у t ;
х 1 t х 1 t ;
х 2 t х 2 t ;
у t у t и т.д.
При линеаризации производные рассматриваются как самостоятельные переменные.
Пути линеаризации
х х у 0
1. Если
близка к линейной в окрестности точки линеаризации, то ее
1, 2,
можно просто заменить линейной зависимостью, и ограничить диапазон изменения
воздействий.
х х у 0
2. Если
не линейна в окрестности точки линеаризации, но непрерывно
1, 2,
дифференцируема, ее можно разложить в ряд Тейлора в этой точке.
х х у 0
3. Если
существенно не линейна, т.е. не является непрерывно
1, 2,
дифференцируемой, а содержит разрывы, неоднозначности и т.п. используют гармоническую
линеаризацию, т.е. при эквивалентном гармоническом воздействии выходную переменную
раскладывают в ряд Фурье. Из него и определяют коэффициенты линеаризации.
34.
Основным является второй путь. Рассмотрим его подробнееУравнение звена в результате разложения в ряд Тейлора примет вид:
( х1о , 0, 0,... хо2, 0, 0,... уо ,0,0...) х1 t х 1 t ... х2 t х 2 t ...
х1 0
х 1 0
х 2 0
х 2 0
... у(t ) у t у t ... (члены высшего порядка малости) 0 (12)
у 0
у 0
у 0
- значение частной производной при подстановке в нее значений переменных и их
производных в точке линеаризации. х1
х1 0
Пренебрегая членами высшего порядка малости и вычитая из уравнения (3) уравнение
установившегося режима (2),получим линеаризованное дифференциальное уравнение звена в
отклонениях или в вариациях:
х1 t х 1 t ..... х2 t х 2 t ...
х1 0
х 1 0
х2 0
х 2 0
... у t у t у t ... 0
у 0
у 0
у 0
(13)
Комментарий:
- Линеаризованное уравнение звена является приближенным, т.к. не учитывает малые высшего
порядка.
- Переменными в уравнении являются отклонения от значений в точке линеаризации.
- Уравнение справедливо при малых отклонениях от значений в точке линеаризации.
35.
Графическая интерпретация линеаризацииу у
у
о
Коэффициенты линеаризации
1
х1
2
х2
х1о
хо2
х1
tg 1
х1 0
tg 2
х2 0
В статических установившихся режимах
у tg 1 x1 tg 2 x2
х2
Рис.45
36. Линейная математическая модель двигателя
Допущения при линеаризации:- точка линеаризации {U яо ; М fо ; Uво ; о} выбрана в рабочем диапазоне изменения воздействий;
- переменные имеют малые отклонения от значений в точке линеаризации;
- характеристика сухих трений линеаризована М трc f стл одним из известных методов
(например, гармонической линеаризации);
Разложим уравнения напряжений и моментов в выбранной рабочей точке линеаризации в ряд Тейлора и
ограничимся рассмотрением лишь линейных членов разложения, отбрасывая члены высшего порядка малости.
Переходя от абсолютных значений переменных к их отклонениям от значений в точке линеаризации, получим
линеаризованные уравнения в отклонениях:
Линеаризованное уравнение цепи якоря в отклонениях
d
U я t E я t URя t ULя t се Фo t се o Ф t R я Iя t Lя Iя t (14)
dt
E я t се Фo t се o Ф t U я t U я t U яo
t t o
- отклонения переменных от их
UR t R я Iя t
Uв t Uв t Uвo
значений в точке линеаризации.
d
ULя t Lя Iя t
Iя t Iя t - Iяо
dt
Линеаризованные уравнения цепи возбуждения и магнитной цепи в отклонениях
Uв t URв t ULв t R в Iв t Lв
d
Iв t
dt
Ф t Iв t
(15)
Линеаризованное уравнение моментов в отклонениях
Мэм t М f t Мтрс t Мдин t ,
или
d
Мэм t см Фo Iя t см Iяо Ф t M f t f трл t J д t
М эм t см Фo Iя t см Iяо Ф t
М трс t f трл t
d
Мдин t J д t J д t
М f t М f t М fо dt
(16)
dt
- отклонение моментов от их значений в точке линеаризации.
37. ЛИНЕАРИЗОВАННАЯ ДИНАМИЧЕСКАЯ МОДЕЛЬ ДПТ НВ в изображениях
Перейдем в уравнениях (14) – (16) от переменных во времени к их изображениям по Лапласу:U я t U я s ; Uв t Uв s ;
Iя t Iя s ; E я t E я s ;
М f t М f s ; t s ;
Ф t Ф s ; М эм t M эм s
Получим линеаризованные уравнения для цепей двигателя в изображениях:
U я s се Фo s се o Ф s R я Iя s Lя s Iя s
(17)
Uв s R в Iв s Lв s Iв s (R в Lв s) Iв s
(18)
Ф s Iв s
(19)
Мэм s см Фo Iя s см Iяо Ф s M f s f трл s J д s s
(20)
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА ДПТ НВ
Uв(s)
Iв(s)
1
R в L вS
Фв(s)
о
U я(s)
1
Iя(s)
R я L яS
М тр ( s )
I яо
Фо
См
М эм ( s )
J рs
Мf (s)
Ея(s)
Фо
Се
Рис.46
1
(s )
38. Передаточная функция ДПТ НВ при управлении по цепи якоря
Uв(s)1
Iв(s)
R в L вS
Фв(s)
М тр ( s )
о
U я(s)
1
R я L яS
Iя(s)
f трл
I яо
См
Фо
М эм ( s )
(s )
1
J р sJ р sf тр
Мf (s)
Ея(s)
Фо
Се
1 Jp s
Рис.47 Преобразованная структурная схема
1 f тр1 J p s
1
J p s f тр
Cм Фо /( R я L я s)(J p s f тр )
Cм Фо
1 се см Фо2 R я Lя s J p s f тр J p L я S2 (J p R я L я f тр )S Cм Се Фо2 R я f тр
2
*
/(
С
С
С
Ф
Ф
R я f тр )
о
о
м
м
е
К
(s)
WUя
(
)
Jp Lя
2 J p R я L я f тр S 1
Т 22 s2 T1s 1
S
См Се Фо2 R я f тр
См Се Фо2 R я f тр
1 / Се Ф о
К
;
При Мтр=0 W U (s)
2
я
Jp Lя 2
Jp R я
s
1
S 1 Т я Тм s Tм
2S
2
С м Се Ф о
С м Се Ф о
J
W
U я (s)
где:
Т я Lя
Rя
;
Тм
р Rя
се см Фо2
(21)
(22)
(23)
(24)
39. Передаточная функция ДПТ НВ по возмущающему воздействию
СеФо
М тр ( s )
Ея(s)
1
R я L яS
Фо
См
Рис.48 Преобразованная структурная схема
W
Мf (s)
1 /( J p s f тр )
2
С
С
Ф
о
е
м
1
(L я s R я)(J p s f тр )
М эм ( s )
1
J р Js р sf тр
Mf (s)
R я Lя s
;
2 (
2
)
S
J p Lя S
J p R я Lя f тр
Cм Се Фо R я f тр
* 1
-R я (1 Т я s ) /( См Се Фо2 R я f тр )
К
Tя s
f
2 2
(
)
Jp Lя
2 J p R я L я f тр S 1
Т 2 s T1s 1
S
См Се Фо2 R я f тр
См Се Фо2 R я f тр
2
-К f 1 T я s ;
(s) -R я (1 Т я s ) / См Се Фо
При Мтр=0
W Мf
2
Jp Lя 2
Jp R я
s
Т
Т
Tм s 1
я
м
S
1
S
Rя
См Се Фо2
См Се Фо2
Kf
се см Фо2
W
Мf (s)
(s )
(25)
(26)
40. Передаточная функция ДПТ НВ при управлении по цепи возбуждения
Uв(s)1
Iв(s)
R в L вS
Фв(s)
Се
о
М тр ( s )
I яо
(R я Lяs)
Фо
1
R я L яS
Ея(s)
Се
Iя(s)
Фо
См
М эм ( s )
1
(s )
J рs
Фо
Рис.49 Преобразованная структурная схема
2
/(
С
С
С
Ф
Ф
R я f тр )
о
о
м
м
е
I
яо (
s
s)
R я L я се о
W Uв
(
)
J p Lя
s
2 J p R я L я f тр S 1
Ф
R в Lв о
S
См Се Фо2 R я f тр
См Се Фо2 R я f тр
*
Кв (1 Т я s)
s
W Uв
(1 Тв s)[ T22 s2 T1s 1]
Тя
о Iяо R я
Lв ; Т*
;
(
1
);
я
где: Кв
Тв
1 сеФо о Iяо R я
Rв
R в Фо се Фо о
(27)
(28)
41.
ПРИНЦИПИАЛЬНАЯ СХЕМА ЭЛЕКТРОМЕХАНИЧЕСКОЙ ТРАНСМИССИИГ
ИD
ОЯг
Mf Г Г
E ЯГ
M ТР Г M Г
ОЯд
IЯ
E ЯД
UЯ
Ф BД
Ф BГ
U BГI BГ
MТР Д Mfд
КОд
КОг
д
MД
U BД
ОВг
I BД
ОВд
Рис.50
Условные обозначения на схеме:
Элементов:
Г – генератор;
ИД – исполнительный двигатель;
ОЯг – обмотка якоря генератора;
ОЯд – обмотка якоря двигателя;
ОВг – обмотка возбуждения генератора;
ОВд – обмотка возбуждения ДПТ;
КОг – компенсационная обмотка генератора;
КОд – компенсационная обмотка двигателя;
i = г,д (генератор или двигатель)
Переменных
U я i t , Uв i t - напряжения на зажимах цепи якоря и цепи
возбуждения i - ой машины ;
t
,
t
Iя i
Iв i - токи в цепи якоря и цепи возбуждения i-ой машины;
Фвi t - поток цепи возбуждения i- ой электромашины;
E яi t - ЭДС якоря i - ой машины ;
М эмi t - электромагнитный момент на валу i - ой машины;
М fi t - внешний возмущающий момент на валу i - ой машины;
Мтрi t - момент трения на валу i - ой машины;
i t - скорость вращения вала i - ой машины.
42.
Нелинейная математическая модель электромеханической трансмиссии(при принятых ранее допущениях):
двигатель
генератор
d
d
Iяд U яг сег Фг г R яг I яг Lяг Iяг
dt
dt
d
d
Uвд R вд Iвд Lвд Iвд
Uвг R вг Iвг Lвг Iвг
dt
dt
Уравнение цепи якоря: U яд сед Фд д R яд I яд L яд
Уравнение цепи возбуждения:
Уравнение магнитной
цепи :
Фвд
Iвг при Iвг Iвнасг
при Iвд Iвнасд
Фвг г Sign при
Фнасг
Iвг
Iвг Iвнасг
Фнасд Sign Iвд при Iвд Iвнасд
д Iвд
Мэмг М fг Мтрсг Мдинг ;
Мэмг смг Фг Iяг
d
Мдинг Jг г Jг г
dt
Мэмд М fд Мтрсд Мдинд ;
Электромагнитный момент ;
Мэмд смд Фд Iяд
d
Динамический момент:
Мдинд J д д J д д
dt
Уравнение моментов:
Момент сухих трений
на валу:
Мтрд
Мтрсд Sign д при д 0
Мтрсг Sign г при г 0
(М эмг - М fг ) при г 0 и
(Мэмд - М fд) при д 0 и
Мтрг
Мэмд М fд М трсд
М эмг М fг М трсг
Мтрсг Sign (Мэмг - М fг )
М трсд Sign (Мэмд - М fд) при д 0
при г 0 и Мэмг - М fг М трсг
и Мэмд М fд М трсд
U яд U яг U я
Уравнения связи:
и
Iяд Iяг Iя
сег Фг г сед Фд д R яд Iя R яг Iя Lяд
где:
R ягд R яг R яд
и
d
d
d
L
Iя
R
I
L
I
ягд
ягд я
я
Iя яг
dt
dt
dt
Lягд Lяг Lяд
(29)
43.
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМЕХАНИЧЕСКОЙ ТРАНСМИССИИМ трд
L яг D
L яд D
г
С ег
Е яд
I вг
Ф нас
I нас
1
R вг L вг D
М трг
М динг
М эмг
М fг
1
R яд
Iя
Фд
U вг
С мд
1
JД D
М эмд
М fд
R яг
Фг
JдD
Uя
Е яг
С ед
С мг
Рис.51
I вд
Ф нас
I нас
1
R вд L вд D
U вд
д
44.
ЛИНЕАРИЗОВАННАЯ ДИНАМИЧЕСКАЯ МОДЕЛЬ трансмиссиив изображениях
Перейдем в уравнениях от переменных во времени к их изображениям по Лапласу:
U я t U я s ; Uв t Uв s ;
Iя t Iя s ; E я t E я s ;
М f t М f s ; t s ;
Ф t Ф s ; М эм t M эм s
Получим линеаризованные уравнения для цепей двигателя в изображениях:
U я s се Фo s се o Ф s R я Iя s Lя s Iя s
Uв s R в Iв s Lв s Iв s (R в Lв s) Iв s
Ф s Iв s
Мэм s см Фo Iя s см Iяо Ф s M f s f трл s J д s s
и линеаризованные уравнения для цепей генератора в изображениях:
U яг s сег Фoг г s сег oг Фг s R яг Iяг s Lяг s Iяг s
Uвг s R вг Iвг s Lвг s Iвг s (R вг Lвг s) Iвг s
Фг s г Iвг s
Мэмг s смг Фoг Iяг s смг Iяог Фг s M fг s f трлг г s Jг s г s
45.
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМЕХАНИЧЕСКОЙ ТРАНСМИССИИМ трд
г
С ег
Ф го
Е яг
Фг
М динг
М эмг
М fг
г
I вг
С мг
С мд
Ф до
М эмд
1
R вг L вг s
Фд
U вг
д I вд
до
С ед
д
1
JДs
М fд
I яо
I яо
М трг
Iя
Е яд
го
J г s f трг
1
R ягд L ягд s
f трд
1
R вд L вд s
U вд
Ф до
Ф го
Рис.52
Примечания:
-Переменные в схеме Рис.52 являются изображениями по Лапласу отклонений соответствующих
переменных от их значений в выбранной точке линеаризации;
- s - комплексная переменная преобразования Лапласа;
- R ягд R яг R яд - суммарное активное сопротивление якорной цепи двух машин;
- L ягд L яг L яд - суммарная индуктивность якорной цепи двух машин;
- f трг , f трд - коэффициенты линеаризованных трений на валах генератора и двигателя.
46.
Передаточные функции электромеханической трансмиссииПередаточная функция от
г
Ф го
г
до
С ег
М трд
д
Е яг
1
R ягд L ягд s
Iя
Е яд
д
W
г (s)
iт
С мд
С ед
Ф до
Рис.53
СегФго Смд Фдо /(Смд Сед Ф2до R ягд f трд )
(
)
J pд Lягд
2 J pд R ягд L ягд f трд S 1
S
2
Смд Сед Фдо R ягд f трд
Смд Сед Ф2до R ягд f трд
- передаточное число трансмиссии.
Передаточная функция
от
fг
fд до
М
Ф до
1
R ягд L ягд s
М
М fг
Iя
Ф до
С мд
Е яд
Смг
f трд
М эмд
1
д
JДs
1 iт
2
s2 Tгд1s 1
Тгд2
М трд
М эмд
(30)
f трд
1
д
JДs
М fд
Ф го
С ед
Ф до
/(Смд Сед Ф2до R ягд f трд )
Сед Фдо /( J pд s f трд ) R ягд Lягд s
С
Ф
до
ед
I
W Мя f (s)
2
(J pд R ягд Lягд f трд )
J pд Lягд
Сед Смд Фдо
2
S 1
1
S
2
2
(Lягд s R ягд)(J pд s f трд )
Смд Сед Фдо R ягд f трд
Смд Сед Фдо R ягд f трд
Рис.54
Сед Фдо /(Смд Сед Ф2до R ягд f трд )
С
Ф
го
мг
1 iт
fг (s)
Wм
мfд
2
2
(
)
J pд Lягд
s
Т
Tгд1s 1
2 J pд R ягд L ягд f трд S 1
гд2
S
Смд Сед Ф2до R ягд f трд
Смд Сед Ф2до R ягд f трд
(31)
47.
ПРИНЦИПИАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО РЕГУЛЯТОРА СКОРОСТИ3 220 v
Г
ИD
ОЯг
Mf Г Г
ПD
E ЯГ
M пд
M ТР Г M Г
IЯ
UЯ
I BГ
ОВг
д
MД
I BД
O
MUo
ОУ
MТР Д
Ф BД
U BД
РЕД
E ЯД
КОд
КОг
Ф BГ
U BГ
ОЯд
Mfo
ОВд
Рис.55
На схеме дополнительно обозначено :
ПД – приводной двигатель;
РЕД – редуктор;
ОУ – объект управления;
Mпд М fг - момент на валу приводного двигателя;
i Р - передаточное число редуктора;
Р
- КПД редуктора;
- управляющее воздействие (момент) на объект управления;
Uo
M
MРo - момент реакции объекта управления;
Mfo - возмущающий момент на объект управления;
O - регулируемая переменная (скорость вращения ОУ).
Mfд i Р Р
MРo
48.
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО РЕГУЛЯТОРА СКОРОСТИМ трд
L яг p
L яд р
U вг
хх
I вг
1
R вг L вг p
Фг
Ф нас
I нас
С ег
Е яг
г
пд
R яг
пд
1
1
R яд
Е яд
М трг
М fг
М эмг
М динг
С ед
1
С мд
JДр
Ф нас
I нас
I вд
Мро
М втро
С мг
Рис.56
г пд ххпд пд
пд Мпд стпд ;
Мпд М fг Мэмг Мтрг Мдинг
Мдинг ( J пд J г ) d г dt
о д ip ;
М ро
М д М fд
i p p
М дино
U вд
Допущения
ПД имеет жесткую линейную механическую характеристику на рабочем участке;
Электромагнитная постоянная ПД пренебрежимо мала;
Редуктор жесткий безлюфтовый;
ОУ уравновешен и имеет сухие и вязкие трения в оси.
Уравнения для ПД, редуктора и ОУ
о
1
i р
1
R вд L вд р
Фг
1
iр
д
М fд
Фд
J Г p
СТпд
М f ПД
Uя
М эмд
Iя
f втро
Jор
М стро
М ро М uo
М fо
Мuo Мpo М fo Мтрo Мдинo
М трo М тpвo М трсo
f тро о M трсо sign o
Мдинo J o d o dt
49.
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО РЕГУЛЯТОРА СКОРОСТИ(при Uвд=const и приведении свойств ОУ к оси исполнительного двигателя)
М втрод f втро
i 2 р
L яг p
М строд
М трдо
L яд р
I вг
U вг
хх
1
R вг L вг p
Фг
Ф нас
пд
г
пд
1
Uя
R яг
1
R яд
М трг
М fг
М эмг
Iя
1
С Мд Ф д
J ДО р
д
М fд
1
i р
Е яд
J Г p
СТпд
М f ПД
С ег
I нас
Е яг
М эмд
С Ед Ф д
М динг
М fо
Фг
С мг
Рис.57
На схеме введены обозначения:
J о - приведенный к оси двигателя момент инерции системы;
J до J д 2
i p
М стро M втро
- приведенные к оси двигателя трения системы.
2
М трдо М стрд
i p
i p
1
iр
о
50.
ЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО РЕГУЛЯТОРА СКОРОСТИМ трдо ( s)
U вг (s )
1
R вг L вг S
г
хх ( s) пд ( s) г ( s)
пд ( s)
G пд
f трг
го
1
R ягд L ягд
С мг
На схеме введены обозначения:
I я ( s) М эмд ( s)
С Мд Ф д
S
1
J ДО S
М fд ( s)
Е яд ( s)
Ф г ( s)
J Г S
М эмг ( s)
С ег
Ф го
М f ПД ( s) М трг ( s) М динг ( s)
М fг ( s)
Е яг ( s)
Ф г ( s)
I вг ( s)
f трдо
1
iр
о ( s)
д ( s)
1
i р
С Ед Ф д
I Яо
М fо ( s)
Ф го
Рис.58
Jо
- приведенный к оси исполнительного двигателя момент инерции системы;
J до J д 2
i p
f стро f втро - коэффициент приведенных к оси исполнительного двигателя
f трдо f трд
линеаризованных трений системы;
i 2 p
J Г ; f трг - суммарный момент инерции и коэффициент линеаризованных суммарных трений на валу Г и ПД;
1
- модуль мягкости механической характеристики ПД.
G ПД
СТпд
51.
Передаточная функция электромашинного регулятора скорости по управляющему воздействиюпри жесткой механической характеристике ПД (
)
СТпд
С ег г г / i p C мд Ф д /( R ягд L ягд s )( J до s f трдо )
2
( R вг L вг s)
С ед С мд Ф д
1
( L ягд s R ягд )( J до s f трдо )
С ег г г / i p
C мд Ф д
( R вг L вг s) J до L ягд S 2 ( J до R ягд L ягд f трдо ) S C мд С ед Ф 2д R ягд f трдо
С ег г г / i p
С мд Ф д /( С мд С ед Ф 2д R ягд f трдо )
К
( R вг L вг s)
( J до R ягд L ягд f трдо )
J до L ягд
( Т вгs 1)(Т 22 s 2 T 1 s 1)
2
S 1
S
2
2
С мд С ед Ф д R ягд f трдо
С мд С ед Ф д R ягд f трдо
W U Овг ( s)
Передаточная функция электромашинного регулятора скорости по возмущающему воздействию
1 / i 2p p ( J до s f трдо )
W МОfо ( s)
1
С ед С мд Ф 2д
( L ягд s R ягд )( J до s f трдо )
(R ягд L ягд s)/ i 2p p
J до L ягд S ( J до R ягд L ягд f трдо ) S C мд С ед Ф 2д R ягд f трдо
2
R ягд ( 1 Т ягд s ) /( С мд С ед Ф 2д R ягд f трдо ) i p p
2
( J до R ягд L ягд f трдо )
J до L ягд
2
S 1
S
2
2
С мд С ед Ф до R ягд f трдо
С мд С ед Ф д R ягд f трдо
К f ( Т ягд s 1)
(Т 22 s 2 T 1 s 1)
52.
ПРИНЦИПИАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО МОМЕНТНОГО ПРИВОДАпри косвенном измерении момента и компенсации противо ЭДС
3 220 v
Г
ИD
ОЯг
Mf Г Г
ПD
E ЯГ
M пд
M ТР Г M Г
IЯ
UЯ
УУ
U Мо
КК
U
ЭУ
BГ
BAD
I BГ
ОВг
MД
DМ
DС
Рис.59
РЕД
I BД
O
MUo
ОУ
MТР Д
Ф BД
U BД
д
E ЯД
КОд
КОг R ш
Ф BГ
U Мз
ОЯд
Mfo
ОВд
Mfд i Р Р
MРo
53.
ЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО МОМЕНТНОГО ПРИВОДА(R вг Lвг s)
К эу г СЕг г
U кк ( s)
U мз ( s)
U вг (s )
К эу
U мос ( s)
I вг ( s)
1
R вг L вг S
г
С Ед Ф д
М трдо ( s)
f трдо
I я ( s) М эмд ( s)
Ф г ( s)
о ( s)
1
1
1
С Мд Ф д
г С Ег
iр
J ДО S
R ягд L ягд S
Е яг ( s) Е яд ( s)
М fд ( s) д ( s)
1
С Мд Ф д
i р
С Ед Ф д
M Uo ( s)
К осм
iр
f трд
J дs
Рис.60
М fо ( s)
54.
ПРИНЦИПИАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО( ЭМУ поперечного поля)
усилителя мощности
3 220 v
ЭМУ
Rш
M пд
ПD
пд
ОП
E ЯII
КОэму
Ф ко
Ф рII
ОЯэму
U //
Ф
Mг
I Я E Я
I II
Zн
Ф р
Условные обозначения
ОДП
U У1
U У2
I У1
ОУ1, ОУ2 - обмотки управления
ОЯэму - обмотки якоря ЭМУ;
Фу
ОДП, ОП - обмотки дополнительных полюсов и
ОУ1
I У2
ЭМУ;
КОэму
ОУ2
подмагничивания;
- компенсационная обмотка ЭМУ;
EЯ , I Я - ЭДС и ток поперечной цепи якоря ;
EЯ// , IЯ// - ЭДС и ток продольной цепи якоря ;
Рис.61
55.
ПРИНЦИПИАЛЬНАЯ СХЕМА ЭЛЕКТРОМАШИННОГО РЕГУЛЯТОРА СКОРОСТИс ЭМУ поперечного поля
3 220 v
ЭМУ
Rш
M пд
ПD
пд
ОП
E ЯII
КОэму
Ф ко
ИD
IЯ
Mfo
Ф рII
ОЯэму
Mг
I Я E Я
I II
ОЯд
UЯ
Ф
I У1
Ф р
U У2
I У2
Фу
д
РЕД
MТР Д
КОд
Ф BД
U BД
ОУ1
ОУ2
Рис.61
I BД
O
MUo
ОУ
E ЯД
ОДП
U У1
MД
ОВд
Mfд i Р Р
MРo
56.
Математическая модель регулятора скорости с ЭМУПри принятых допущениях ЭМУ можно описать следующими уравнениями:
Uу R у Iу Lу
dI у
M dI Mкя dI // ;
dt
dt
dt
M ; M кя
-взаимная индуктивность ОУ с обмотками
поперечной и продольной цепи ЭМУ,
- ЭДС поперечной цепи ЭМУ,
Е Се пд [Ф у Ф р Фко Ф р // ] Се пд Ф//
ОУ, КО и реакций
Ф у у I у ; Фко ш к I// ; Ф р Ф I ; Ф р// // I // потоки
обмоток якоря ЭМУ
Ф р// Фко // (1 ш к // ) I // // I // ; - коэффициент недокомпенсации
dI // - напряжение на зажимах
Е // Се пд Ф - ЭДС продольной цепи ЭМУ, U // Е // R // I // L //
поперечной цепи ЭМУ.
dt
ЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА РЕГУЛЯТОРА СКОРОСТИ С ЭМУ
М РII S
I II ( s)
II
U у(s)
Ф IIк ( s)
I у ( s) Ф у ( s) Ф II ( s)
1
R у L уS
у
М трдо ( s)
Е ( s)
пд С е
Ф р ( s)
I ( s)
1
R L S
Ф ( s)
Е II ( s)
пд С е
М эмд ( s)
1
1
С
Ф
д
Мд
J ДО S
R IIд L IIд S
I я ( s)
М fд ( s)
Е яд ( s)
1
i р
М Р S
С Ед Ф д
М fо ( s)
Рис.62
f трдо
д ( s)
1
iр
o ( s)
57.
Схема одноплечевого ШИП с системой симметричного управленияИП
U гпн
TV 1
СУ
U вх
СС
D1
U1
ГПН
РИ
Uп
2
RЯ
Uн Uя
У
Iн Iя
TV 2
реверс
U вх
- U вх
U гпн
Uп
2
t
Т
Uн
t
Iн
ИП- импульсный преобразователь;
СУ- система симметричного управления;
ГПН- генератор пилообразного напряжения;
СС- схема сравнения;
РИ- распределитель импульсов;
У- усилители;
- относительная длительность импульса U1.
t
U
п
2
Рис.64
t
Условные обозначения:
U1
U2 Т
ЕЯ
D2
U2
Диаграммы напряжений
LЯ
нагрузка
Рис.65
Uп
2
58.
Схема мостового ШИП с системой симметричного управленияИП
U гпн
СУ
U1
ГПН
U вх
СС
РИ
Временные диаграммы
U п
RЯ
Uн Uя
У
Iн Iя
TV 2
D3
ЕЯ
U4
D2
Рис.66
LЯ
нагрузка
TV 4
Uп
D4
U вх
- U вх
U гпн
U 2, U 3
U3
реверс
U вх
Т
TV 3
D1
U2
U 1, U 4
TV 1
t
- U вх
U гпн
t
U1
t
Т
Uн
U2
U4
t
Iн
U3
U п
t
Т
Т
Uн
Iн
t
U п
t
U п
Рис.67 Симметричное управление
Рис.68 Несимметричное управление
59.
Математические представления процессов в ШИПДля симметричного способа управления ШИП на периодах следования импульсов можно
записать:
Н
Н Н Н
Н
nT t n 1 T ,
при
Н
di
E
dt
di
при n 1 T t n 1 T ,
-U R I L
E
dt
U
U 2 для одноплечевых ИП и U U для мостовых схем ИП ,
U
R I L
Н
Н
Н
Н
Н
Н
П
где:
Н
Н
П
При симметричном способе управления напряжение на нагрузке знакопеременное.
Среднее его значение определяется как отношение интеграла за период к периоду Т.
Т
T
1
U пdt
U пdt 2 1 U п
для одноплечевых ИП ,
T
2
2
2
0
T
Т
T
1
1
Uнср Т UПdt T UПdt 2 1 U П для мостовых схем ИП ,
0
T
1
UНСР Т
0 , 0,5 и нср 0
При
У
Для несимметричного способа управления ШИП:
U
U
U
Н
R Н IН LН diН EН
dt
di
0 R I L
E
dt
Т
при
Н
Н
U нср
Н
1
Т
Н
U dt U
П
0
при
Н
П
nT t n 1 T ,
n 1 T t n 1 T ,
среднее напряжение на нагрузке
60.
Статические характеристики ШИПРегулировочная характеристика
UН v
U Н f U У
при постоянных значениях
UП,IН.
250
200
150
100
50
0
U Н f U У
0,5
1
Нагрузочная характеристика
1,5
UУ v
U Н f I Н
UН v
212,2
212,1
212
211,9
211,8
0
10
20
30
IН А
при постоянных значениях
U П ,U У .
61.
Динамические модели ШИПМодель ШИП с симметричным способом управления
Uу
Uгпн
+
Uн
К
-
Uу
Uн
Relay
Модель ШИП с несимметричным способом управления
Uу
Uгпн
Uоп
+
+
-
+
+
+
+
Relay
+
+
К
Uн
Uу
+
Relay
В системах приводов ШИП обычно описывают звеном с малой
постоянной времени или с запаздыванием.
U
W s K У , К У Н
Ts 1
UУ
- коэффициент усиления ,
Т – постоянная времени, равная периоду выходного напряжения.
Uн
62.
ФУНКЦИОНАЛЬНАЯ СХЕМА СКОРОСТНОЙ САР(Электромеханический скоростной следящий привод постоянного тока)
ИD
Mfo
IЯ
U з
УУ
ЭУ
УM
MД
РЕД
O
MUo
ОУ
U Я EЯ
i
MТР Д Mfд Р
U о
ФB
U B IB
BAD
Д
DC
Рис.63
Р
MРo
63.
НЕЛИНЕЙНАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САРМ трд
L яд р
U з
УУ
U
К эу
К ум
Uя
U пит
U вых
U о
U вд
1
R вд L вд р
Е яд
I вд
1
R яд
Iя
1
С мд
М fд
Фд
Ф нас
М эмд
I нас
1
iр
JДр
д
1
i р
f втро
С ед
М дино
М тро
М ро М uo
М fо
К дс
Рис.69
Jор
о
64.
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САРМ трд
L яд р
U з
УУ
U
К эу
U о
U вд
К ум
1
R вд L вд р
U я
Е яд
I вд
Iя
1
R яд
М эмд
I яо
Фд
М fд
JДр
д
i р
Фо
М дино
М тро
М ро М uo
М fо
К дс
Рис.70
1
iр
1
до
С ед
1
С мд
Фо
f трд
Jор
f тро
о
65.
ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА СКОРОСТНОЙ САР(при приведении к единичной ОС и свойств ОУ к оси двигателя)
М трд
U з
з
1
К дс
УУ
U
W p ( p) К дс
К эу К ум
U я
Е яд
о
1
R яд L яд p
Iя
М эмд
С мд Ф о
М fд
f трдо
1
J до p
д
1
i р
С ед Ф о
М fо
Рис.71
На схеме введены обозначения:
Jо
J до J д 2
i p
f тро
f трдо f трд 2
i p
- приведенный к оси двигателя момент инерции системы;
- приведенные к оси двигателя трения системы.
1
iр
о
66.
Передаточные функции разомкнутой скоростной САРпо управляющему и возмущающему воздействиям
Для получения передаточных функций перейдем в схеме Рис.28 от переменных во времени к их
изображениям по Лапласу. Управляющим воздействием будем считать Зи разорвем обратную связь.
Передаточная функция разомкнутой скоростной САР по управляющему воздействию
W ( s) К ДС К ЭУ К УМ 1
К ДС К ЭУ К УМ 1
C м Ф о /( R яд L яд s )( J до s f трдо )
ip
1
С е С м Ф 2о
( L яд s R яд )( J до s f трдо )
CмФо
i р J до L яд S 2 ( J до R яд L яд f трдо ) S C м С е Ф 2о R яд f трдо
К ДС К ЭУ К УМ С м Ф о /( С м С е Ф 2о R яд f трдо ) i P
J до L яд
С м С е Ф 2о R яд f трдо
S
2
( J до R яд L яд f трдо )
С м С е Ф 2о R яд f трдо
S 1
K
T 22 S 2 T 1 S 1
К
b 2 S 2 b 1S 1
Передаточная функция разомкнутой скоростной САР по возмущающему воздействию
1 /( J до s f трдо ) i 2p P
W fс ( s)
2
СеСмФо
1
( L яд s R яд )( J до s f трдо )
( R яд L яд s ) / i 2p P
2 (
J до L яд S
J до R яд L яд f трдо ) S C м С е Ф 2о R яд f трдо
K fс ( 1 T я s )
R яд ( 1 Т я s ) /( С м С е Ф 2о R яд f трдо ) i 2p P
J до L яд
С м С е Ф 2о R яд f трдо
S
2
( J до R яд L яд f трдо )
С м С е Ф 2о R яд f трдо
S 1
T 22 S 2 T 1 S 1
К fc ( 1 a 1 f s)
1 b 1S b 2 S 2
67.
Передаточные функции замкнутой скоростной САР по управляющему ивозмущающему воздействиям
Полученные выражения передаточных функций разомкнутой САР позволяют представить
структурную схему системы в виде:
М fо ( s )
К f ( 1 a 1f s)
1 b 1S b 2 S 2
з( s )
(s)
о( s )
К
b 2 S 2 b 1S 1
где:
Кf
b1
Рис.72
R яд i 2p P
/
C м С е Ф 2о R яд f трдо
J до R яд L яд f трдо
C м С е Ф 2о R яд f трдо
; K К ДС К ЭУ К УМ
;
b2
CмФо
i p ( C м С е Ф 2о R яд f трдо )
J яд L яд
C м С е Ф 2о R яд f трдо
;
.
Передаточная функция замкнутой скоростной САР по управляющему воздействию
К
К /( К 1 )
К
з
b 2 S 2 b 1S 1
( s )
1
К
b 2 S 2 b1 S 1
b 2 S 2 b1 S 1 К
b2 2
b1
S 1
S
1
1
K
К
К
b 2з S 2 b1з S 1
Передаточная функция замкнутой скоростной САР по возмущающему воздействию
К fc ( 1 a 1 f S)
fс ( s )
1 b 1S b 2 S
1
2
К
b 2 S 2 b1 S 1
- К fс ( 1 а 1 f S)
b 2S
2
b 1S 1 К
К fc
1 К
(1 а1 f S )
b2
b1
S 1
S2
K 1
К 1
- К f з ( 1 а 1 f S)
b 2з S 2 b 1з S 1
68.
Схема одноплечевого ШИП с релейным управлением токаИП
U1
TV 1
D1
RЯ
Uн Uя
U 2 TV 2
Uп
2
нагрузка
LЯ
ЕЯ
Iн Iя
D2
DT
Временные диаграммы
U1
Uп
2
U2 Т
Uп
2
I зад
t
Т
Uн
Iн
t
I зад
Iн Iя
I зад
Рис.73
U
п
2
Рис.74
t
69.
Бесконтактные двигатели постоянного тока (БДПТ)Обращенный двигатель постоянного тока
Fя
Fя
Fр
N
Fр
Fр
Ф
S
Fр
Fя
Fя
Uя
Рис.75
Функциональная схема БДПТ
Uя
ПК
ЭМП
ДПР
ЭМП – электромеханический
преобразователь;
ПК – полупроводниковый коммутатор,
Рис.76
ДПР – датчик положения ротора.
70.
Упрощенная схема БДПТ+
ПК
ЭМП
ФA
Ф AВ
Uя
N
А
S
N
С
В
ФВ
S
А
С
_
ДПР
Рис.77
В
71.
Реверсивная схема БДПТ+
ФАС
ПК
ЭМП
ФA
Uя
S
А
N
ФС
С
В
ДПР
_
72.
73.
74.
Асинхронные исполнительные двигатели3 220 V
3 220 V
a) Короткозамкнутый ротор
б) фазный ротор
Рис.75
75.
Энергетическая диаграмма асинхронного двигателяN эм
N1
N м 1
N м 2
N с1
N2
N мех
N мех 2
N доб
Рис.76
Г- образная схема замещения одной фазы асинхронного двигателя
R1
Х1
I 2
R
U1
Х 2
R 2
S
I
Х
Рис.77
76.
Уравнение статической механической характеристики АДСкорость вращения поля статора:
где:
60 f 1
n1
p
f 1 - частота питающего напряжения;
s f2
Скольжение:
[об/мин]
[рад/с]
(38)
Р - число пар полюсов.
ns n1 n2
Скорость проскальзывания ротора:
2 f 1
1
p
60 f 2
p
n
1 2
1 n2
f1
n1
1
,
f2
- частота токов в роторе.
(39)
Из энергетической диаграммы АД:
Nм2 Nэм Nмех Мэм 1 Мэм 2 Мэм ( 1 2) Мэм 1 s
2
Потери в меди ротора ( Джоулевы потери): N м2 m R 2 I 2
m R 2 I 22
Приравнивая (38) и (39), получим:
M эм
1 s
Из схемы замещения:
I 2
U1
R1 R 2 s 2 X1 X 2 2
(40)
(41)
(42)
(43)
Уравнение статической механической характеристики АД:
m U12 R 2 s
m U12 R 2 s
Mэм
2
2
2
2 2
1 R1 R 2 s X
1 R1s R 2 X s
Координаты точек экстремума характеристики:
2
2 2
2
dM эм m U12 R 2 [ R1s R 2 X s ] R 2 s[2 R1 (R1 s R 2) 2 X s]
2
2
ds
2
2
1
(R s R ) X s
R 2 R1 X s
2
2
2
1
2
(44)
0
77.
Критическое скольжение и критический момент асинхронного электродвигателяИз последнего уравнения выразим скольжение, которое соответствует экстремумам зависимости
и называется критическим скольжением:
sкр R 2
Mэм f ( s)
R1 X
2
2
(45)
Подставляя выражение (45) в уравнение (44), получим выражение для экстремальных значений
электромагнитного момента АД, которые называются критическими моментами:
2
Мкр
2 1
m U12
R12 X 2 R1
(46)
Mэм f ( s) и 2 f (Мэм) .
2 , получим:
С учетом скольжение: s 1
1
s 0 ( 2 1) , Mэм 0 - идеальный холостой ход;
s 1 ( 2 0) , - режим короткого замыкания;
Характерные точки зависимостей
крт
1 sкр
0
кр sкр
Мкр Mкрт Mкз
1
0
1.
Mэм
2.
MкзМкрт Mкр Mэм
кр
m U12 R 2
(47)
Мэм Мкз
2
2
1 R1 R 2 X
3. s ( 2 ) , Mэм 0 - режим ТПВ;
4. s ( 2 ) , Mэм 0 - режим РТ.
Используя характерные точки, построим механическую
характеристику асинхронного двигателя на плоскости " Mэм "
1
крт
кр 1 1 Sкр
крт 1 1 Sкр
- скорости вала АД, соответствующие
экстремумам в двигательном и
тормозном режимах.
Характеристику легко перестроить в зависимость Mэм f s
s
Рис.78
Можно также построить характеристику при другом направлении
вращения вала АД на холостом ходу.
78.
Уточненная и упрощенная формулы КлоссаВозьмем отношение
Мэм
к
Мкр
2
2
2
2
2(1 R1 R12 X2 )
М эм 2 R 2 s R1 X (1 R1 R1 X )
2 2
2
2 2
2
2 2
2 R1 R 2 s
R1 s X2 s
Мкр
R1 s 2 R1 R 2 s R 2 X s
s R 2 R12 X2 s R 2 R12 X2
R 22
s R 2 R12 X2
2
2
2
2
R1 R1 X и учитывая sкр R 2 R1 X , получим:
2 Мкр (1 )
- уточненная формула Клосса
(48)
М эм
S Sкр
Для АД особенно большой и средней мощности:
2
Sкр S
R1 X (R1 0,1X )
sкр R 2 Х
следовательно.
0
2 Мкр
Тогда получим: М эм
(49)
- упрощенная формула Клосса
S Sкр
Sкр S
Вводя обозначение
Мкр
Мн
Nн
Мн
н
- допустимая перегрузка АД по моменту, указана в паспортных данных двигателя.
- номинальный момент АД;
1 н
Sн
1
1
Из упрощенной формулы Клосса для номинального режима
- номинальное скольжение АД;
2
Sн Sкр
Sкр Sн
легко найти
Sкр
79.
Изменение числа пар полюсов двухскоростного АДS
N
N
S
N
N
S
N
S N
N
S
S
a2
a1
а1;а2
A
X
a1
A
a2
A
X
X
в)
б)
a)
Рис.79
Переключение обмоток статора АД из звезды в двойную звезду
В
А
С
а
b
b
В
x y
z
А
c
а
Рис.80
x y
z
С
c
80.
Переключение обмоток статора АД из звезды в звезду*В
А
а
С
b
В
b
x y
z
c
x y
z
c
а
С
А
Рис.81
Переключение обмоток статора АД из звезды в треугольник
В
А
А
С
С
В
x
b
b
а
x y
z
y
c
z
а
Рис.82
c
81.
Переключение числа пар полюсовИз звезды в звезду (
Из звезды в двойную звезду
2
2
Mкрт
)
1
1
1
1
0
Mкр Mэм
Рис.83 Переключение при постоянном моменте
0
Mкр
Mкр
Mэм
Рис.84 Переключение при постоянной мощности
82.
Переключение из двойной звезды в треугольник2
1
1
Mкр
Mкрт
0
Mкр
Рис.85 Переключение при постоянной мощности
Mкр Mэм
83.
2Регулирование введением добавочного сопротивления в роторе
sкр R 2
Мкр
2 1
3 220 V
R1 X
2
2
m U12
R12 X 2 R1
Rдоб1
Rдоб2
Rдоб 2 Rдоб1
Mкрт
0
Mн
Mкр Mэм
84.
Регулирование изменением частоты питающего напряженияcs
'
кр R 2 Х R 2 2 f 1 L
2
2 f1
2
m U1
mp U1
1
cM U
Мкр
2
2 1 X 2 2 f 1 2 f 1 L
f1
s
При U1 C f
f1
2
0
а)Изменение f1
Mкр
const, Мкр const
C
2
M
Mэм
Mкрт
б) Изменение f1 и U1
0
Mкр Mэм
c поддержанием U1 const
f1
85.
Электромашинная схема частотного управления АД с регулированием U1 и f13 220 v
Г
ИD
ОЯг IЯ
Mf Г Г
ПD
M ТР Г M Г
КОг
УУ
U
BГ
ЭУ
I BГ
ОВг
MТР Д
КОд
U BД
I BД
ОВд
DС
Рис.40
O
MUo
д
ТФГ
Ф BД
Ф BГ
U fз
MД
E ЯД
E ЯГ
M пд
ОЯд
Mfo
ИАD
ОУ
MРo
UU
86.
Функциональные схемы полупроводниковых преобразователей частотыСеть
ИПТ
Сеть
тока
тока
УВ
АИ
Uf
НПЧ
Uf
АИ
д
д
АD
Uf
АD
д
АD
Рис.41
87.
Трехфазный автономный инвертор с асинхронным двигателемТАИ
U1
ОИ
ОИ
TV 1
TV 3
ОИ
+
U3
D3
D1
TV 5
Uс
UВ
UА
D2
Uп
TV 6
U 4 TV 4
U 2 TV 2
D5
U5
U6
D4
D6
-
д
АD
Рис.42
88.
Диаграммы трехфазного инвертора при разных алгоритмах управления1
U1
2
3
4
5
6
U гпн
t
U Амод
U2
U3
t
t
t
U4
U1
U5
t
t
U2
U6
U п
t
UА
t
U п
UА
t
U п
Рис.43 Управление при ШИР на основной частоте
t
U п
Рис.44 Управление при синусоидальной ШИМ
на несущей частоте.
89.
Динамические модели АД при частотном управленииПри частотном управлении АД с поддержанием U1/f1=const потокосцепление машины на рабочем
участке характеристики остается постоянным.
( U1 R 1 I 1)
j 1
При S < Sкр и R1 0
p U1
U1р
j
(
) const
j 2 f 1
2 f 1
При варьировании частоты удобнее пользоваться понятием абсолютного скольжения:
S a 1 2 S 1 ;
1 н
М эм
1н
2 М кр
S a S кн
S кн S а
;
S кн 1 2 кр S кр
1 н
Мкр
1
1н
m 1н U12
( 2 ) const
2 Х н 1
При учете электромагнитной инерции в АД:
М эм
Где:
р
Тэ
d
dt
L
R2
;
2 М кр
S
S
(1 Т э р)( кн [ 1 T э р]) а
Sа
S кн
- оператор дифференцирования;
- электромагнитная постоянная времени.
;
90.
Выполним дифференцирование и получим уравнение движения АДSа
S
( 1 Т э р)( кн ( М Т э рМ)
М 2 М кр
Sа
S кн
( рМ Т э р 2 М) S а (М Т э рМ)р S а S а
S кн
S кн
М
М 2 М кр
Т э рМ Т э S кн
2
Sа
Sа
S кн
Sa
S a2
Мр S a
Тэ
(1
) М 2 Т э рМ Т 2э р 2 М Sa
S 2кн
Sa
Т 2э рМр S a
2 М кр
Sa
S кн
Линеаризуем это уравнение в рабочей точке с параметрами режима
Мо = f( Saо)
2 М о S aо S a Т э Мо р S a
S a
2
2
(1
) М 2 Т э р М Т э р М
2 М кр
S aо
S кн
S 2кн
S 2кн
2
2 М кр 2 М о S aо Т э Мо
S aо
2
2
[( 1
) 2 Т э р Т э р ] М [
р ] S a
2
2
S кн
S aо
S кн
S кн
2
S aо
2
S aо
2 М кр
2 S aо
Т э S 2кн
2
2
[( 1
) 2 Т э р Т э р ] М
[1
р ] S a
2
2
2
2
2
S кн
S кн
S aо S кн S aо S кн
При
Sao=0, Mo=0
получим:
[1 2 Т э р Т 2э р2]М
2Мкр
[1 Т э р]Sa
Sкн
[1 Т э р]М
2Мкр
[ 1 2]
Sкн 1н
91.
[1 Т э р]Мст
2Мкр
Sкн 1н
2Мкр
[ 1 2]
Sкн 1н
L 1н L Xн 1
Тэ
l
l
R 2 1н R2 1н R2 1н S кн
М t М t М t М t 0
эм
U1
f
1
Cf
тр
f 1 2 1
pпол
дин
2
f тр
ст
M эм
M дин
1 Т э р
1
J pP
Mf
2
92.
Основы математического моделирования механических цепей приводаПод механической частью привода понимают ОУ, исполнительный орган двигателя и связывающую
их механическую передачу.
Одним из центральных моментов при решении задач анализа и синтеза приводов является
моделирование свойств реального ОУ, механических цепей регулятора и возмущений.
Это обусловлено положением ОУ в общей схеме системы и видом его связей с узлами регулятора.
Связь ОУ и регулятора носит характер информационно- энергетического взаимодействия:
- с исполнительным двигателем привода энергетическая связь;
- с устройством управления регулятора информационные связи.
ОУ приводов разнообразны, но по связям с регулятором проявляют ограниченное число своих
свойств (свойства, характеризующие ОУ как физическое тело или систему тел).
Взаимозависимость координат связей может быть выражена в различной форме. Наиболее общей
формой ее выражения являются уравнения Лагранжа второго рода для системы масс:
d L
L
( ,)
Mi,
dt i i
где:
L E к Eп
(3)
E к ; E п - кинетическая и потенциальная энергии системы);
i ; ,i - координата и скорость движения i -той массы;
M i - обобщенная сила на i -тую массу.
- функция Лагранжа (
Рассмотрим механические системы приводов и связи ОУ с регулятором и средой для двух случаев:
- привод функционирует в стационарных условиях при силовых f o (t ) возмущениях на ОУ;
- привод функционирует в составе системы стабилизации ОУ, установленной на подвижном носителе.
Система испытывает координатные (линейные V(t ) и угловые к (t ) ) возмущения в плоскости
стабилизации и силовые ( моментные) возмущения на ОУ.
93.
Для конкретного ОУ взаимозависимость переменных его связей с регулятором и средой в первомслучае может быть выражена через свойства объекта:
или
где:
о (t ) F *o ( i , f о , t ) M ou (t )
М ро (t ) F о (M ou , f о , t ) o (t ) , что соответствует различному ориентированию ОУ.
М ро (t ) М ou (t ) - момент реакции ОУ на управляющие воздействия со стороны регулятора;
*
F о и F о - нелинейные операторы ОУ, ориентированного в отношении М рои о.
Момент реакции ОУ можно представить в виде составляющих:
(4)
М ро (t ) М до (t ) М тро (t ) М go (t ) M fo (t )
или М ро (t ) F до ( o , t ) F тро ( o , M o , t ) F go ( o , g , t ) F fo ( f o , o , t ) (5)
где: М до (t ) F до ( o , t ) - динамический момент ОУ ( F до - оператор динамических свойств ОУ);
М тро (t ) F тро ( o , М о , t ) - момент трений ОУ ( F тро - нелинейный оператор трений ОУ);
М gо (t ) F gо ( o , t ) - момент сил тяжести ОУ ( F gо - нелинейный оператор сил тяжести ОУ);
М fо (t ) F fо ( f o , о , t ) - внешний момент на ОУ ( F fо - оператор преобразования внешних сил
на ОУ, например, ветровой нагрузки, в момент возмущения на оси ОУ);
Аналогичное уравнение может быть записано и для исполнительного органа (ИО) двигателя привода,
возмущающим моментом на который является приведенный к оси ИО момент М ро (t ) реакции ОУ,
а
управляющим – теоретический момент
М идт (t )исполнительного двигателя.
М идт (t ) F дио ( иo , t ) F трио ( иo , M иo , t ) F gио ( иo , g , t ) М ро (t )
(6)
Для широкого класса ОУ и приводов, взаимное расположение масс в которых не изменяется,
2
2
операторы динамических свойств ОУ и ИО привода можно представить в виде: F до J o D , F дио J иo D ,
где: J о и J ио - моменты инерции ОУ и ИО привода, D d dt.
Такие операторы линейны, и существуют им обратные операторы
1
F до
1
Jo D
2и
F д 1ио
1
J иo D2
94.
Механические передачи приводов весьма разнообразны (редукторные, кривошипно-шатунные,цепные и т.д.), при этом могут быть с пренебрежимо малыми зазорами (безлюфтовыми) и
деформациями элементов ( жесткими), или с люфтами и упругими свойствами элементов связей.
В первом случае при редукторной связи ИО двигателя и ОУ координаты их движения и
моменты взаимодействия связаны соотношениями:
М ро
где:
,
Мод
о иод ip ;
i p p
ip , р - передаточное число и КПД механической передачи.
(7)
Во втором случае ИО двигателя, механическая передача и ОУ представляют систему тел связанных
упругими элементами при наличии зазоров между ними.
Пренебрегая массами элементов связи, эту двухмассовую систему можно представить в виде схемы:
ио ио
М идт
J ио
С lз
о о
М до
ip , р
Jо
М ро
М троМ fо
2
2
C с2
J
J
o o
ио ио
, где:
Функция Лагранжа системы: L Е k Еп
2
2
2
0
при / / l з - деформация упругих элементов связи ОУ и ИО привода,
с ( )Sign при / /
ио i o , С – жесткость элементов.
lз
lз
М трио
М од
Рис.111
Уравнения движения масс
ИО двигателя:
J ио d ио ,
Миот Мтрио Мод
dt
ОУ:
Мдо Мтро М fо
J о d о ,
dt
Уравнения связи масс:
М од С с С ( / ио i о / l з ) Sign М до i р р ,
при
/ / l з
(8)
95.
Структурная схема системы «ИО – МП – ОУ»при жесткой, безлюфтовой механической передаче
Соответствующая уравнениям (5), (6) и (7) структурная схема механической системы привода
может быть представлена в виде:
*
Оператор ИО двигателя ( F ио )
Оператор МП
с
М тро
-1
F дио
М до
с
М дио
М о
iр
ио
о
с
М до М ро
М gо
1
М gио
F gио
i р р
М fд М од
g
F до
F gо
М fо
F fо
fо
Рис.112
( F о)
F тро
с
М идт
Оператор ОУ
1
М трио F
трио
М ио
( F мп )
g
о
96.
Структурная схема системы «ИО – МП – ОУ»при механической передаче с упругой деформацией элементов и зазорами
Соответствующая уравнениям (5), (6) и (8) структурная схема механической системы привода
может быть представлена в виде:
Оператор МП
Оператор ИО двигателя
*
( F ио )
М идт
М дио
F трио
ио
с
о
С
i р р
iр
М до
М до
с
-1
F дио
с
М gио
М тро
о
( F *о)
F тро
1
F до
с
М ио
Оператор ОУ
М о
М gо
F gио
М fо
с
М трио
( F мп )
F gо
F fо
М fд М од
g
Рис.113
fо
g
о
97.
Схема привода с неуравновешенным ОУy
ay
Fa
rц
x
ax
m
О
Fa
y
Fg
о о
x
98.
о оFax mo ax
Fg mo g
Mg Fg rц Cos o mo g rц Cos o
May Fay rц Cos o mo a y rц Cos o
Max Fax rц Sin o mo ax rц Sin o
Fay mo a y



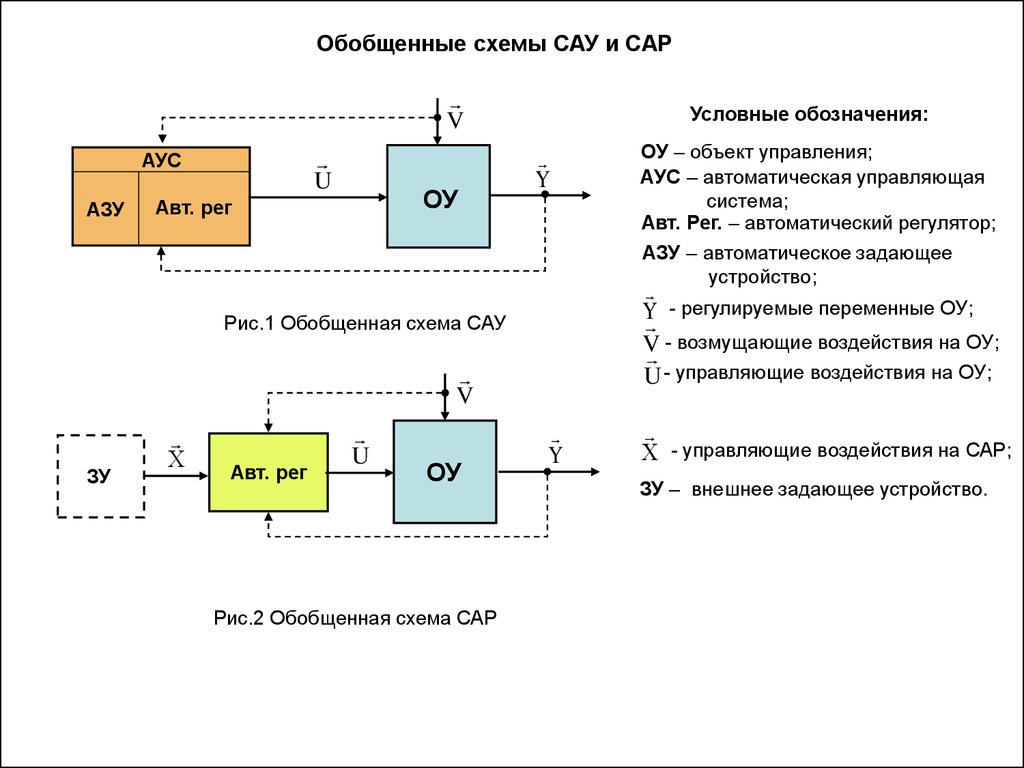


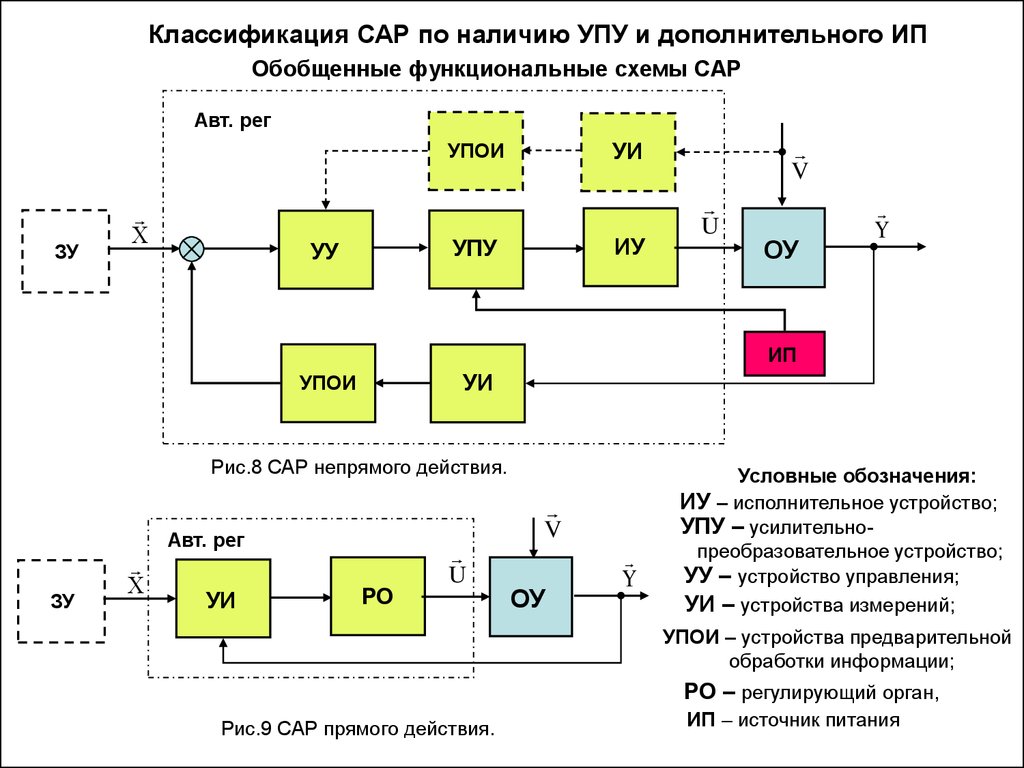
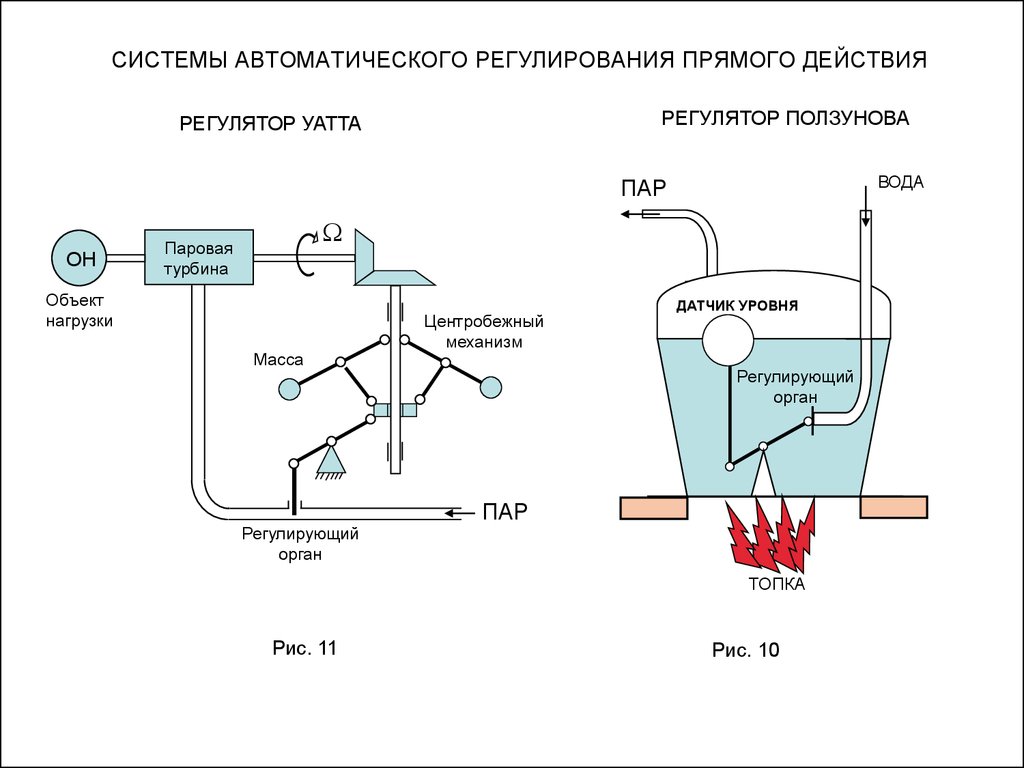

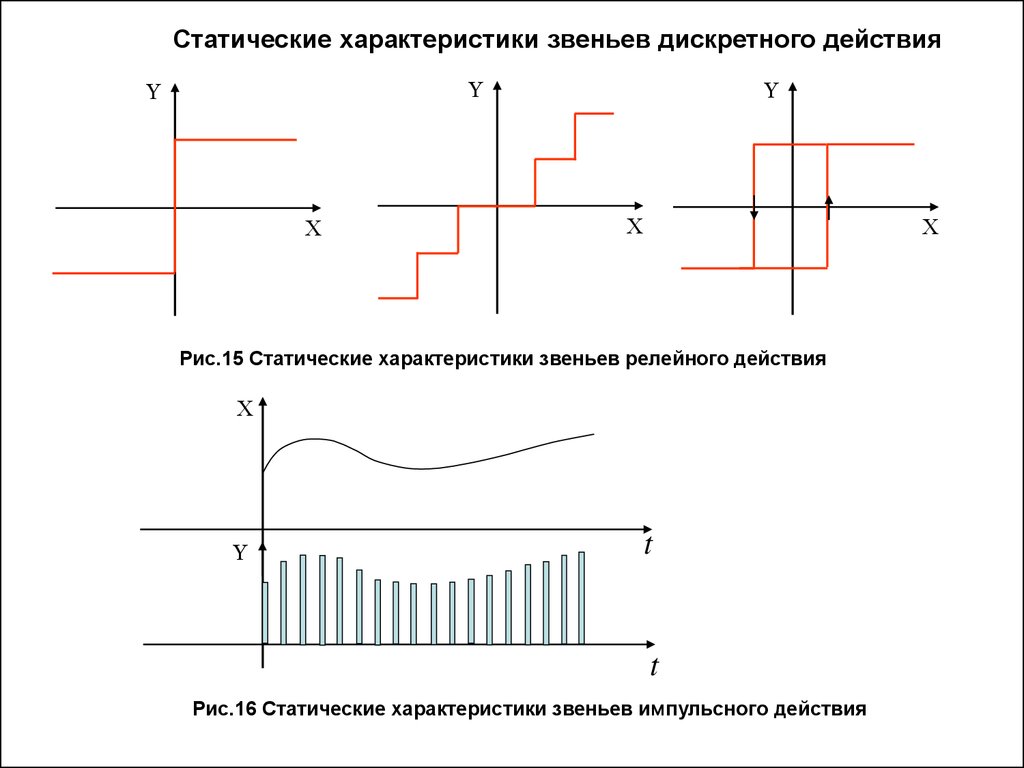
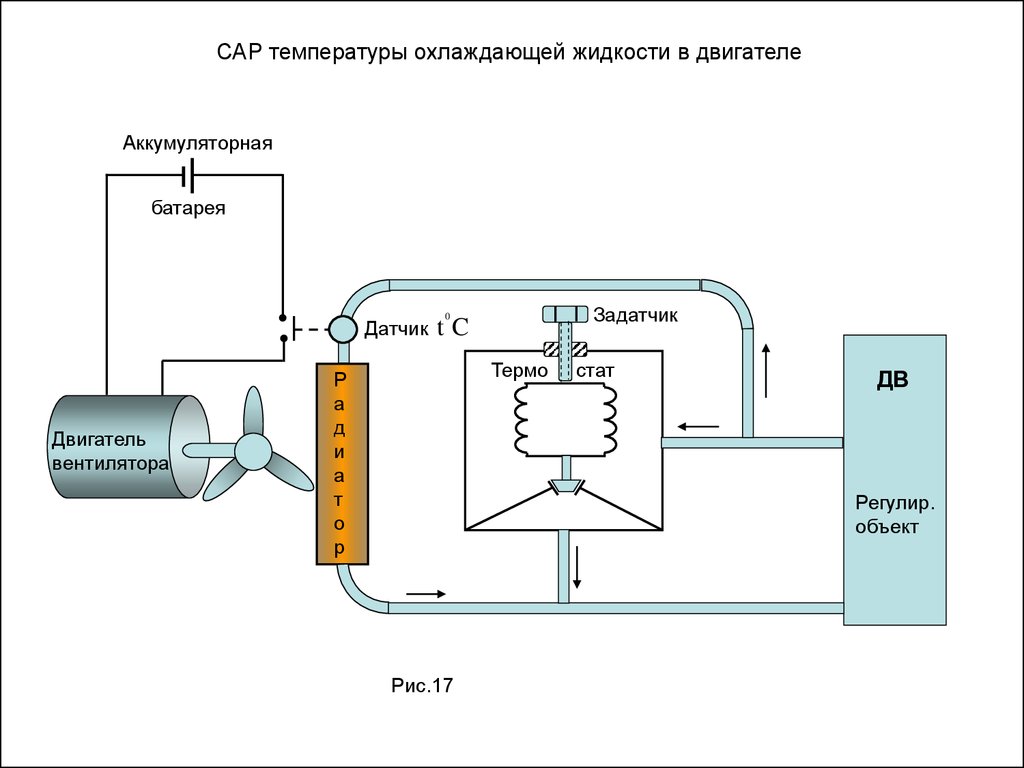
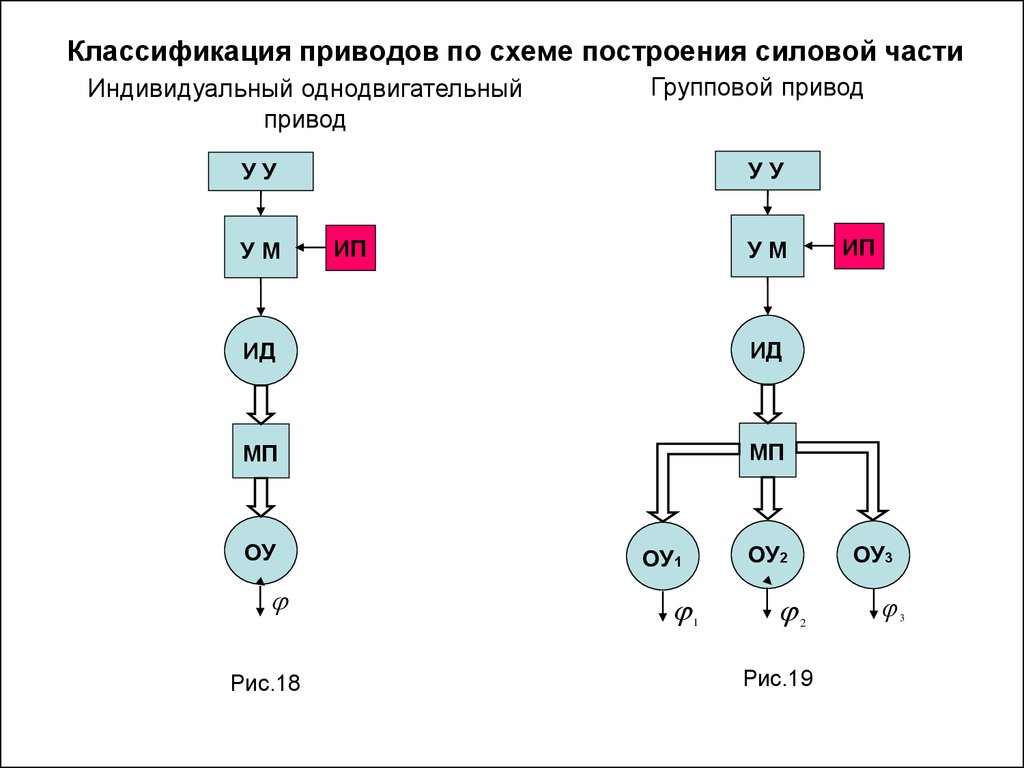


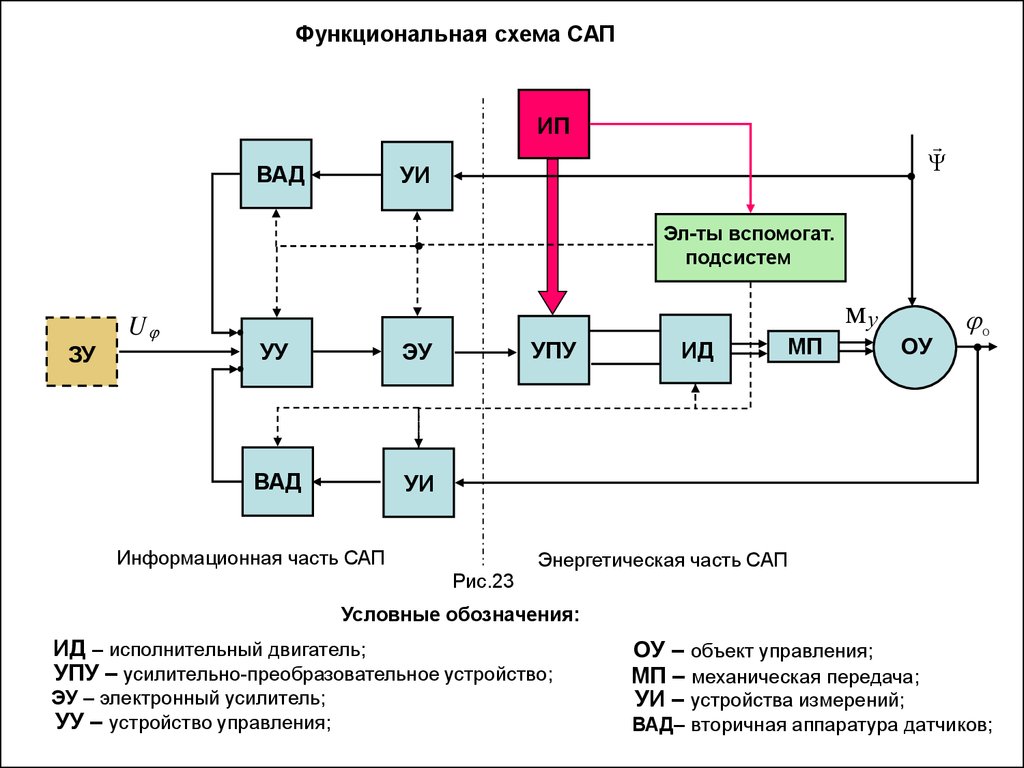


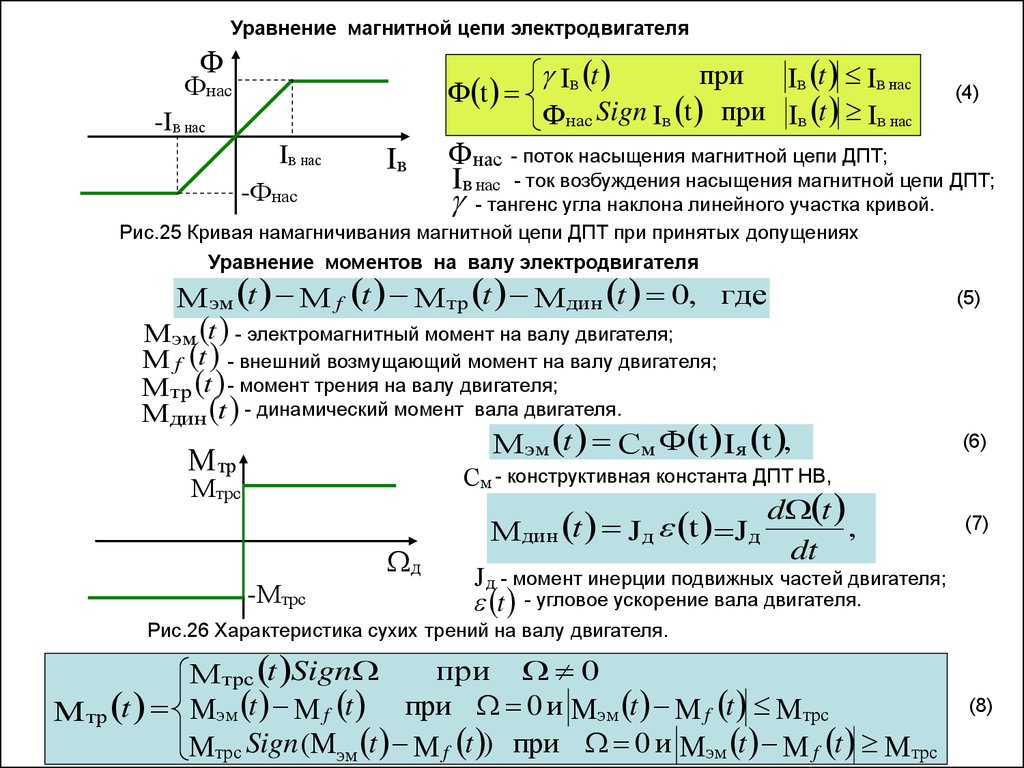

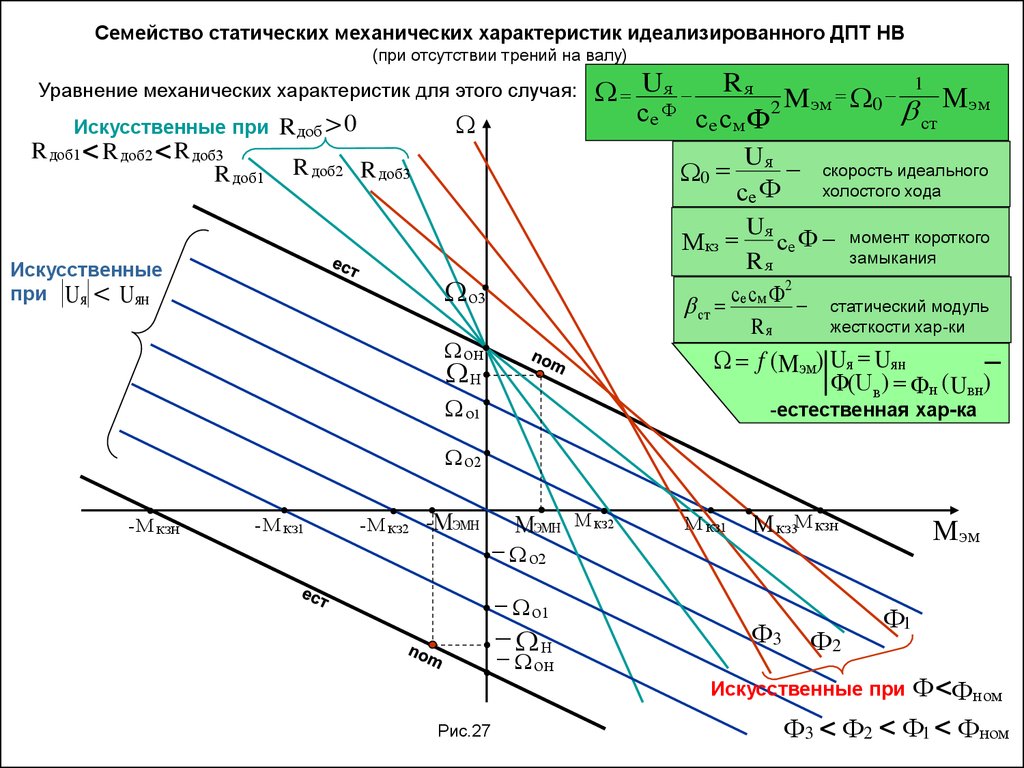









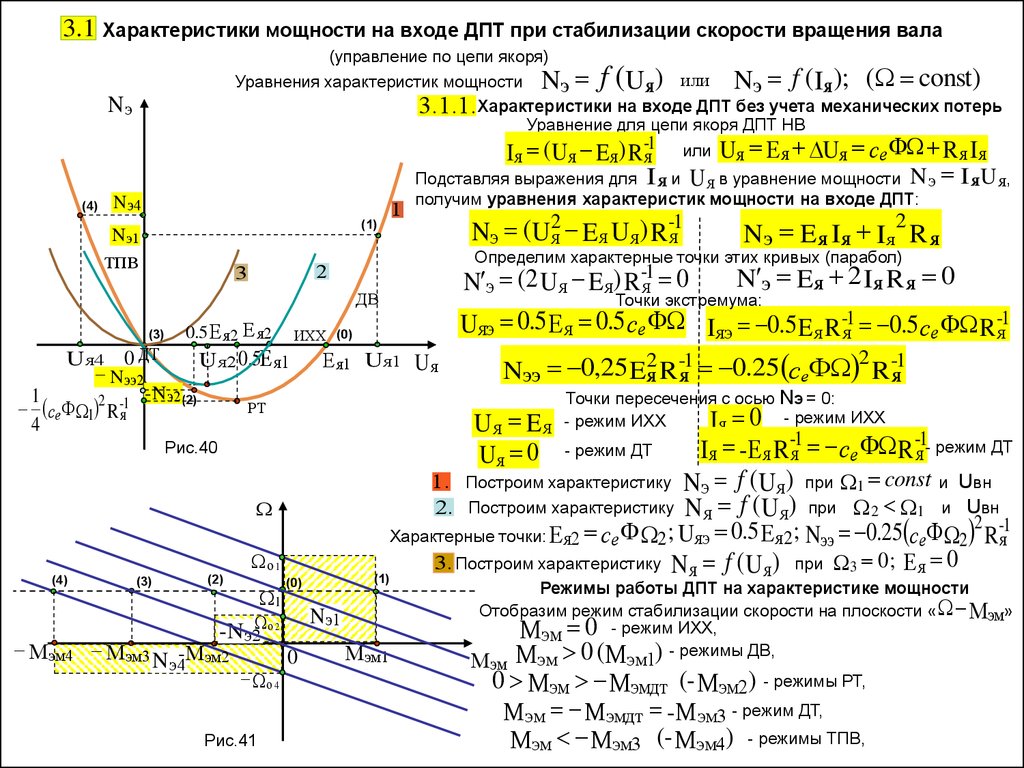

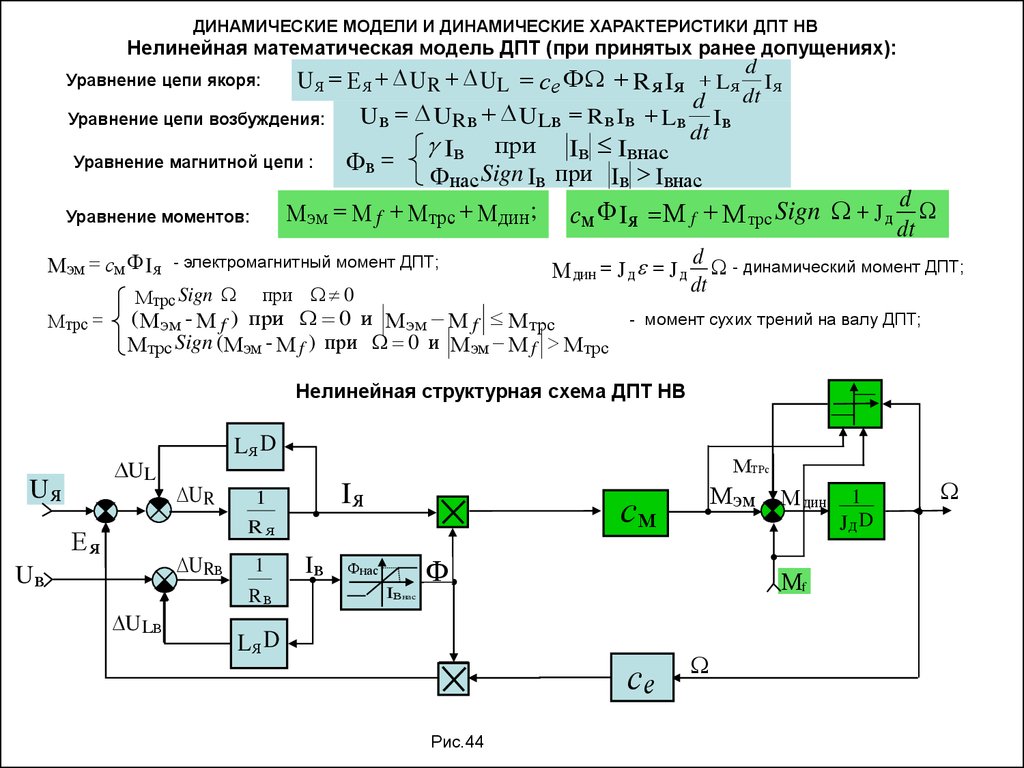




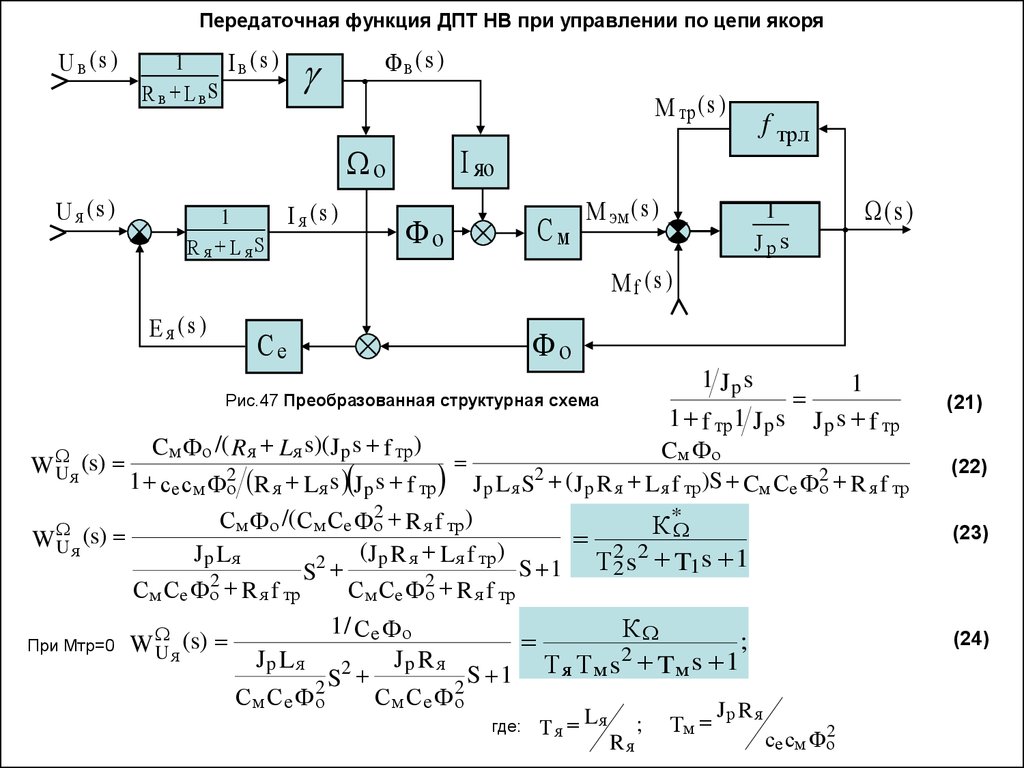
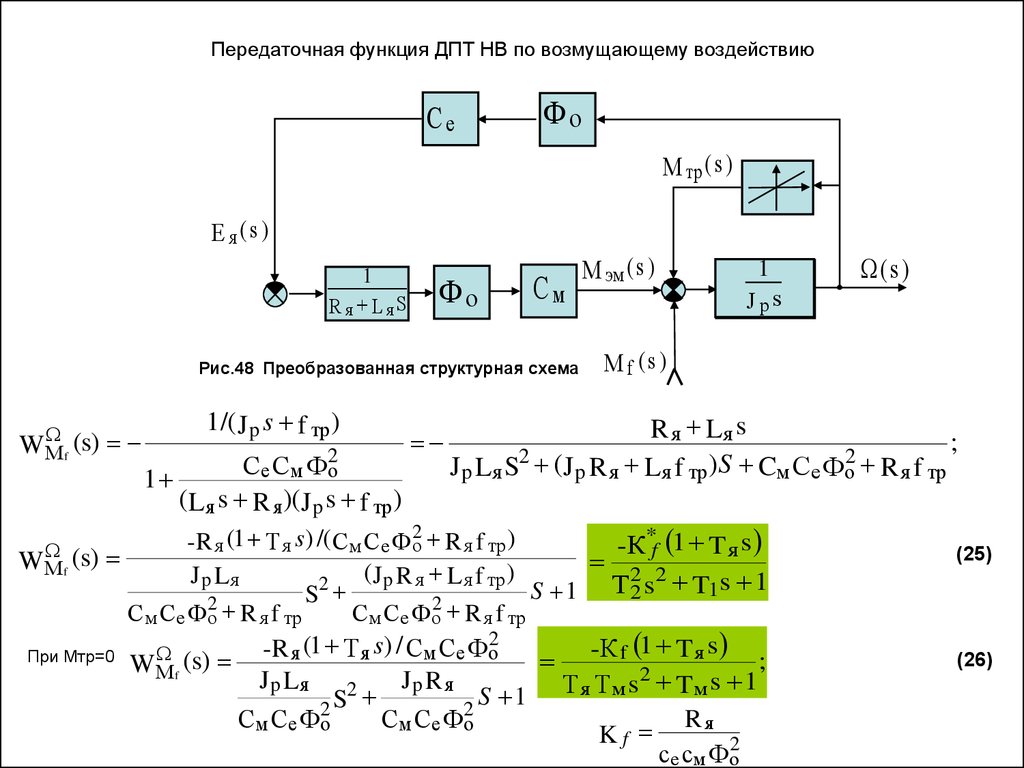


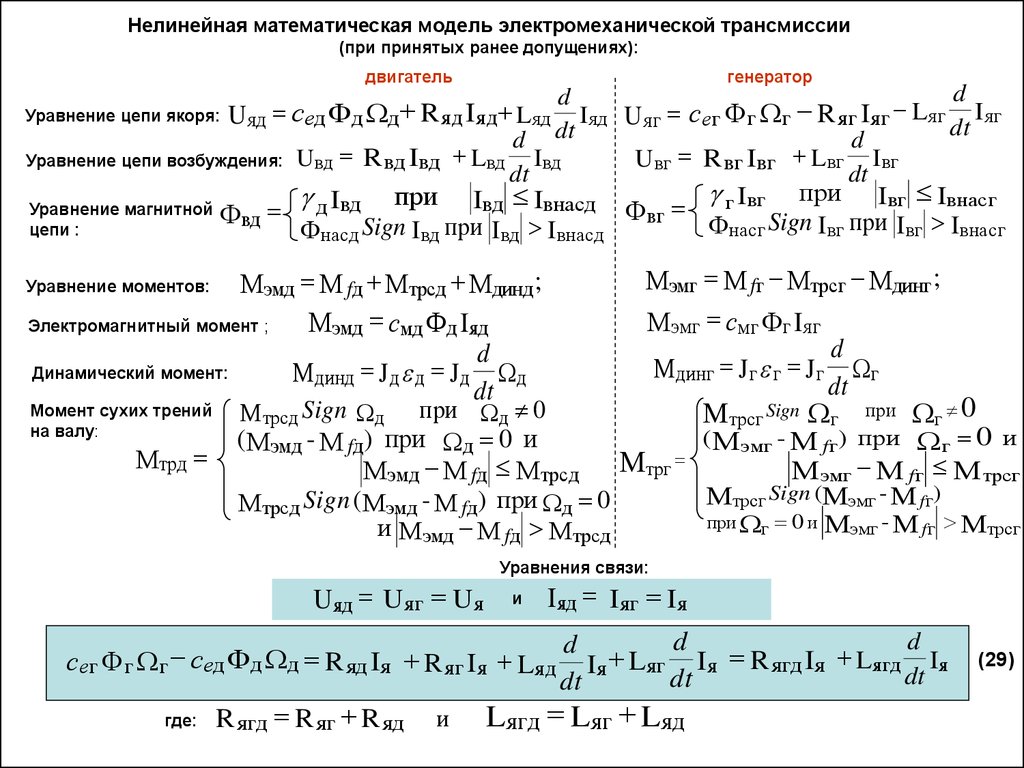








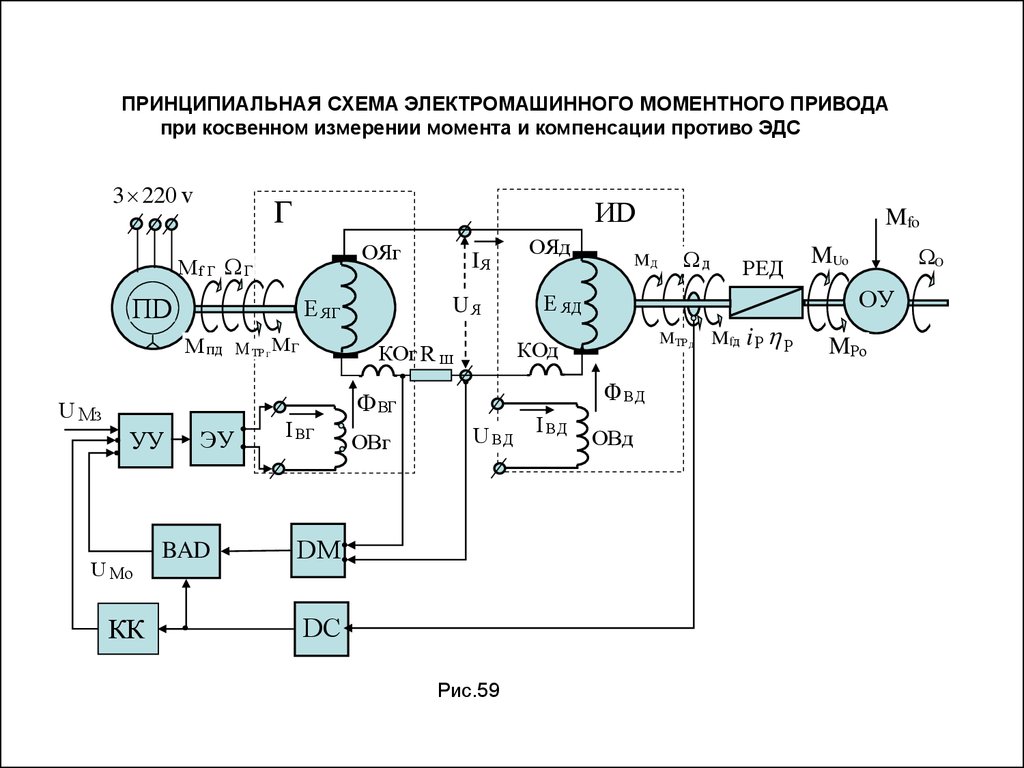


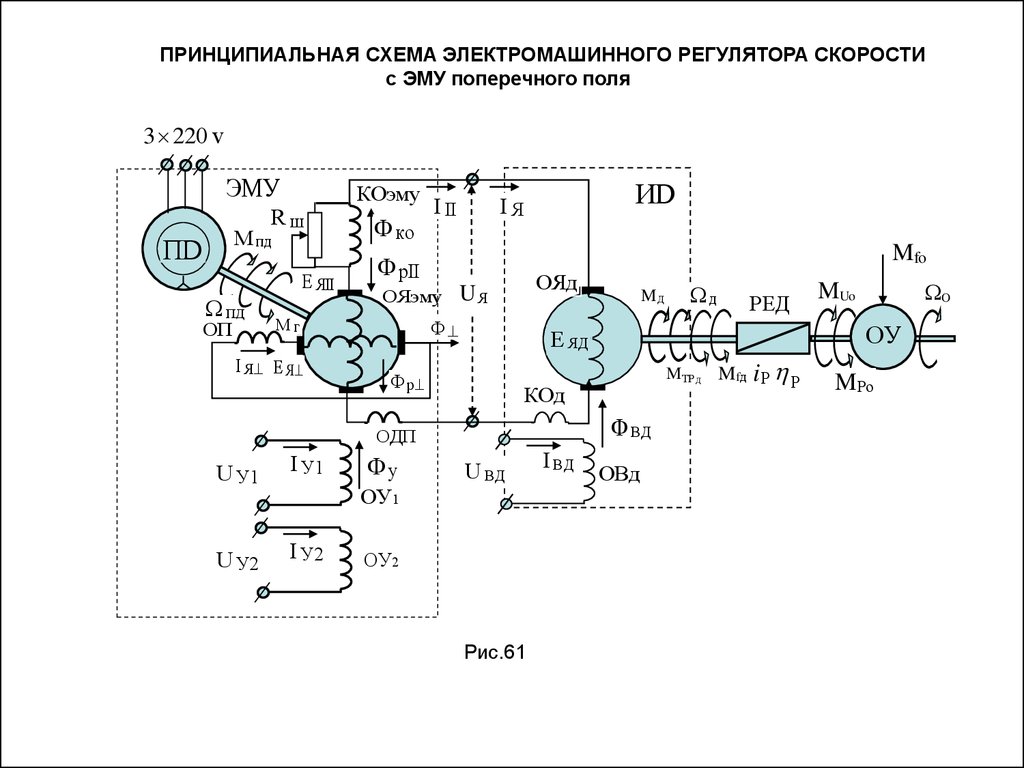

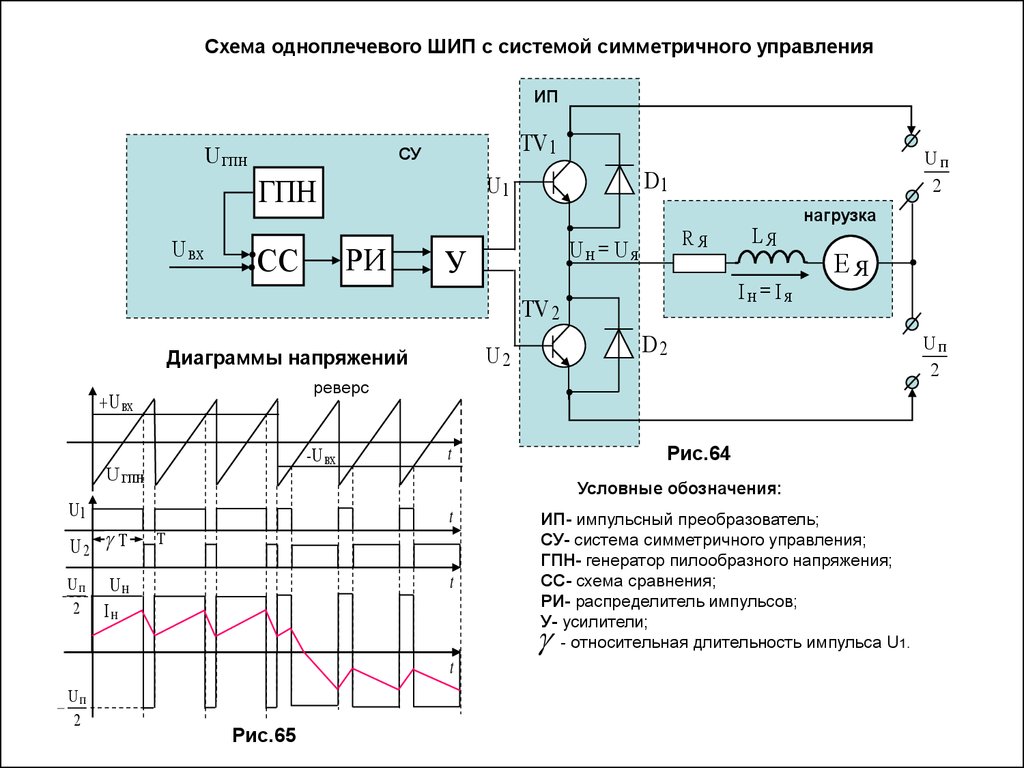



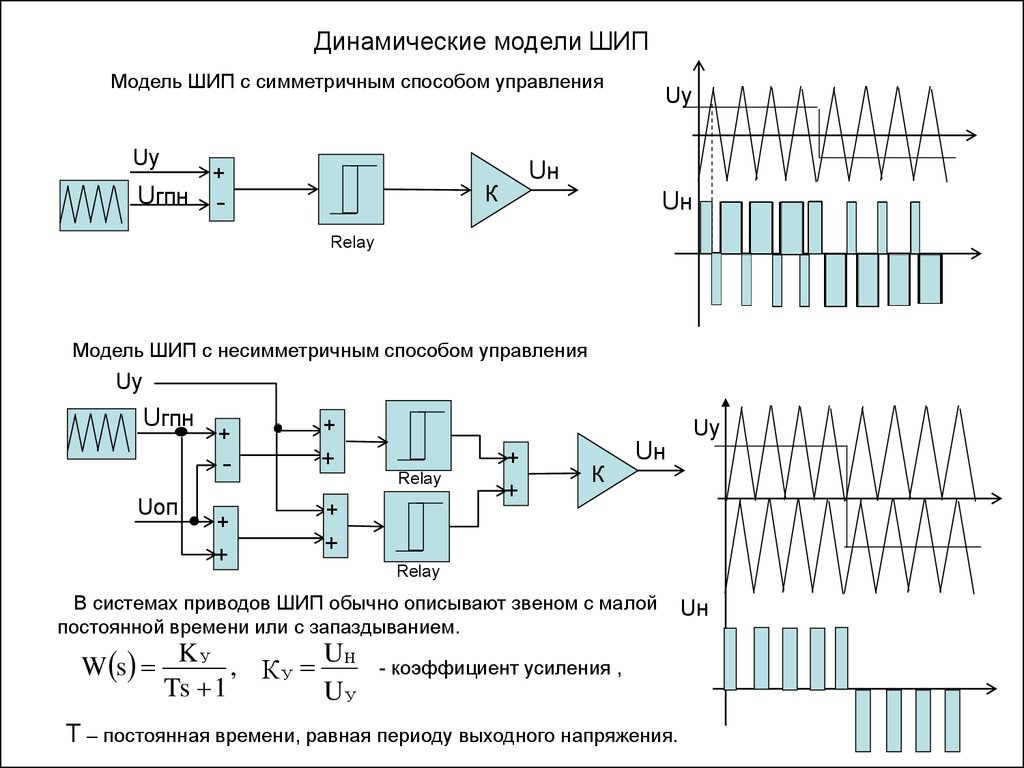



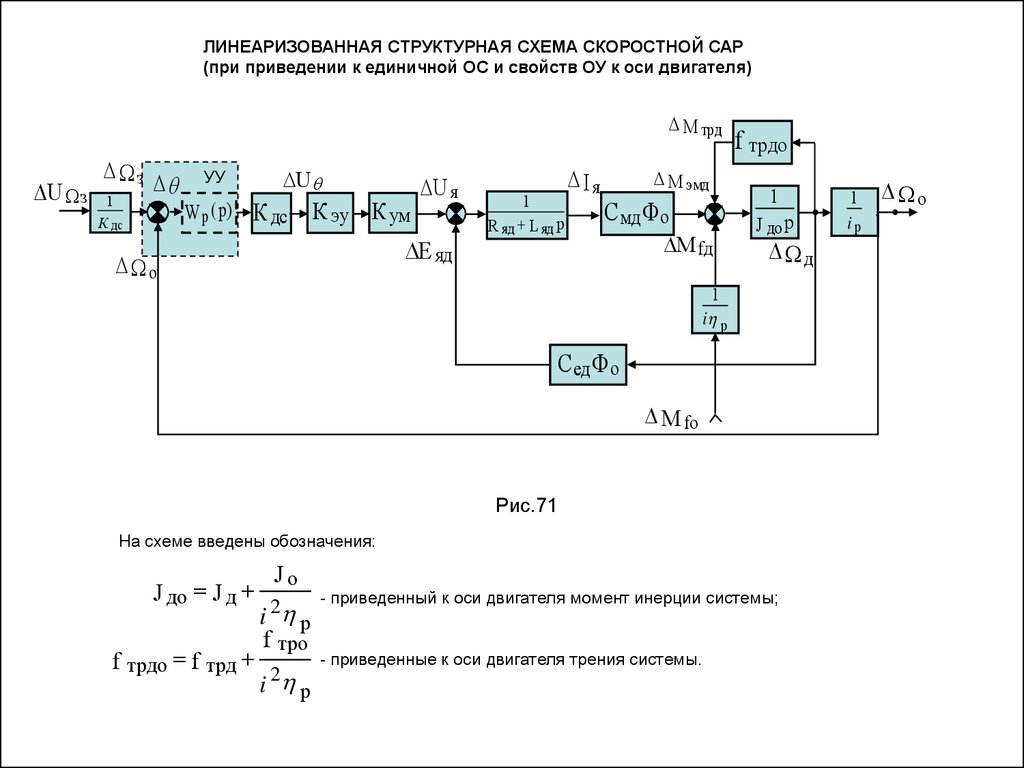

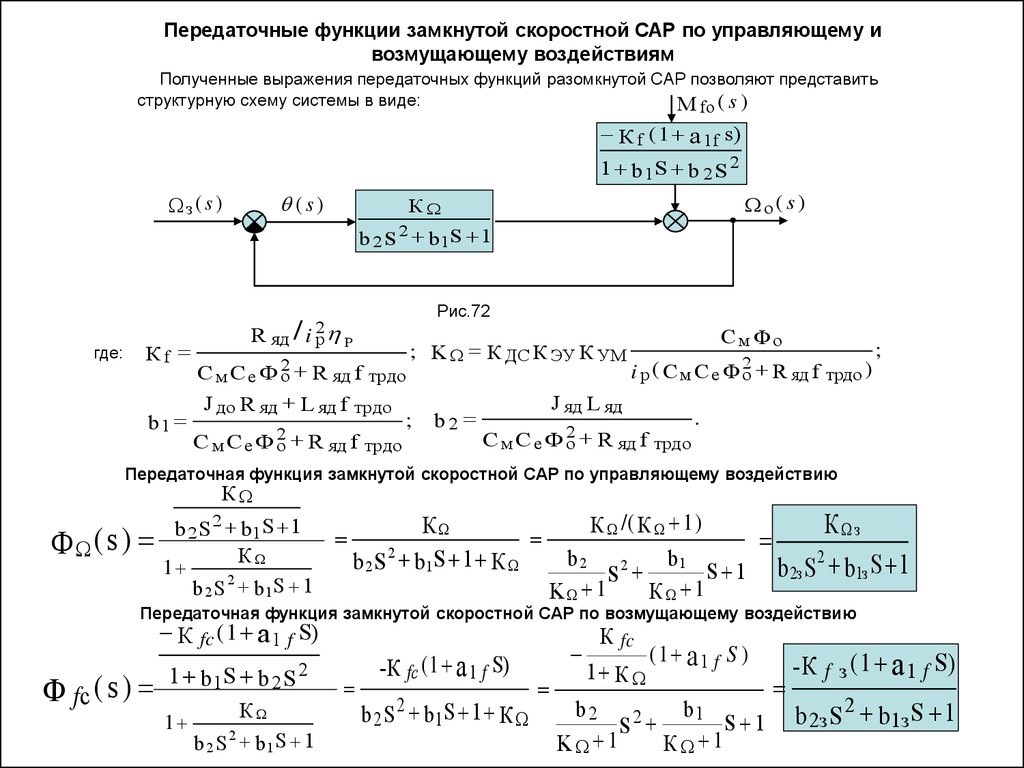
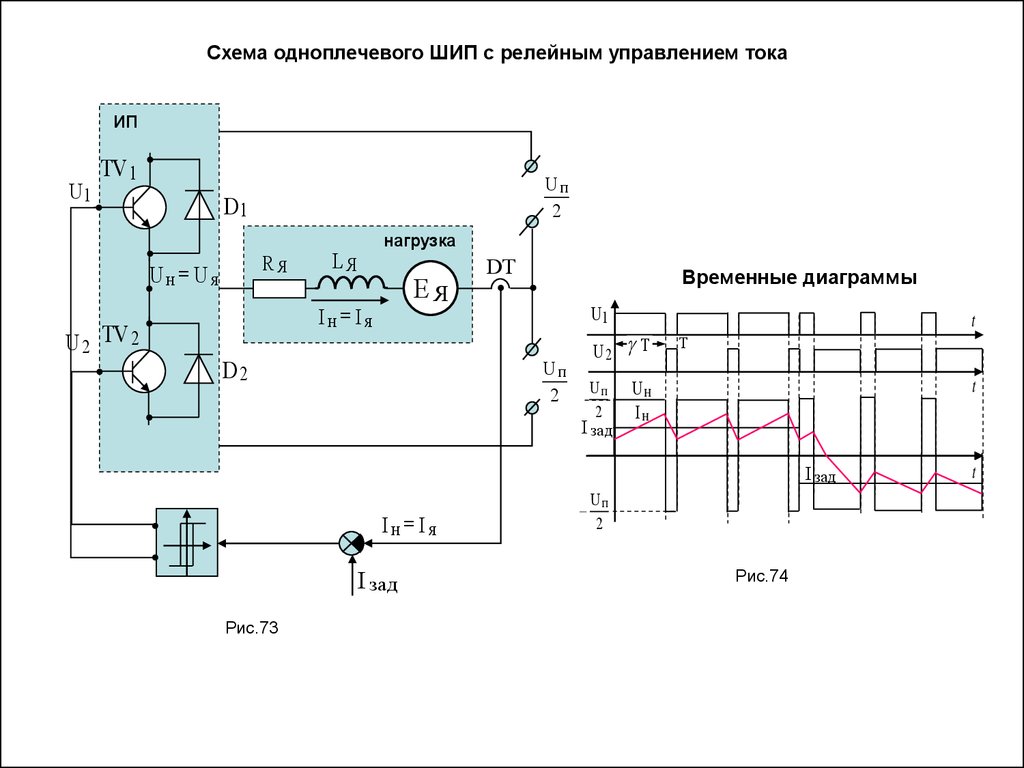
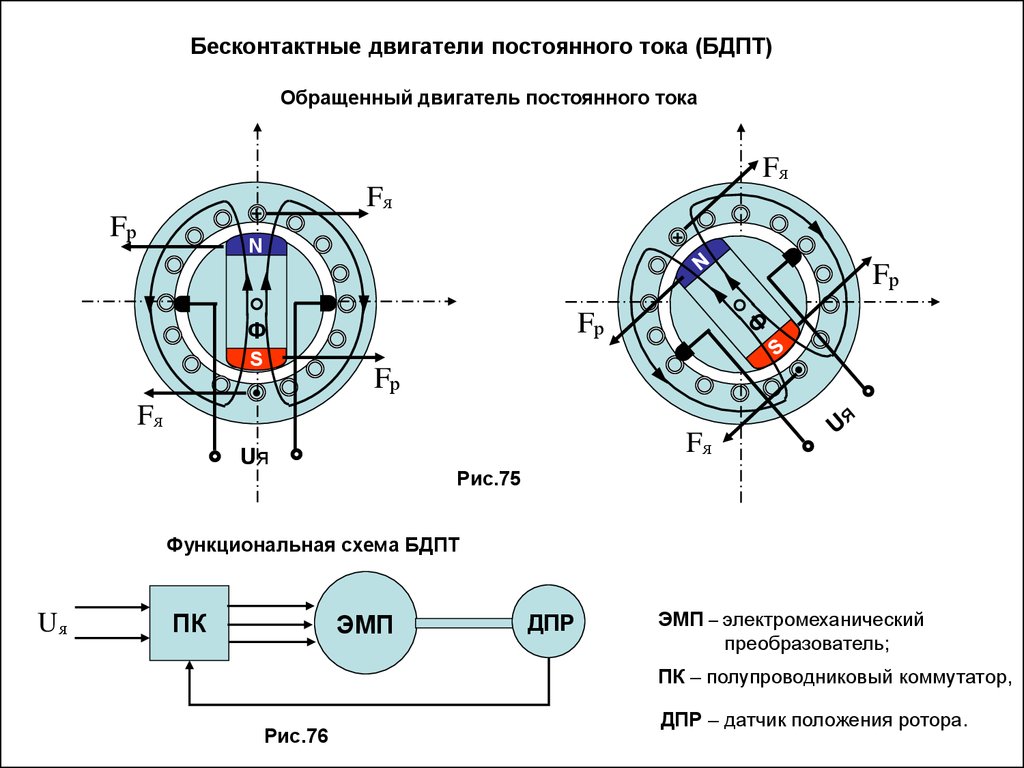



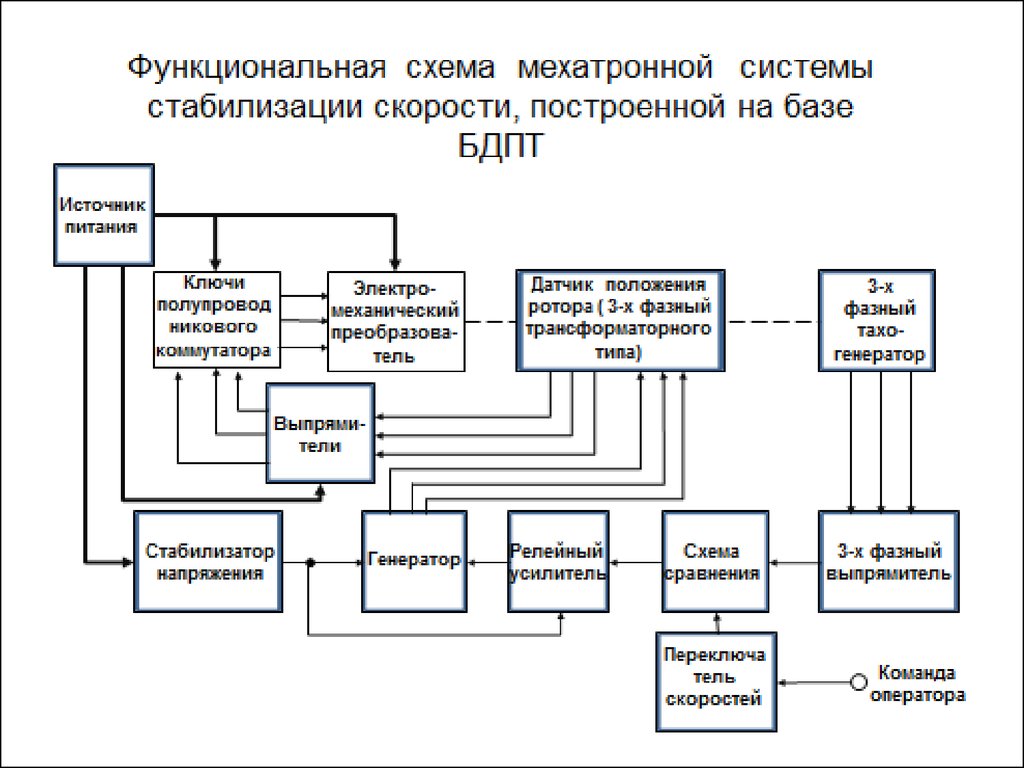

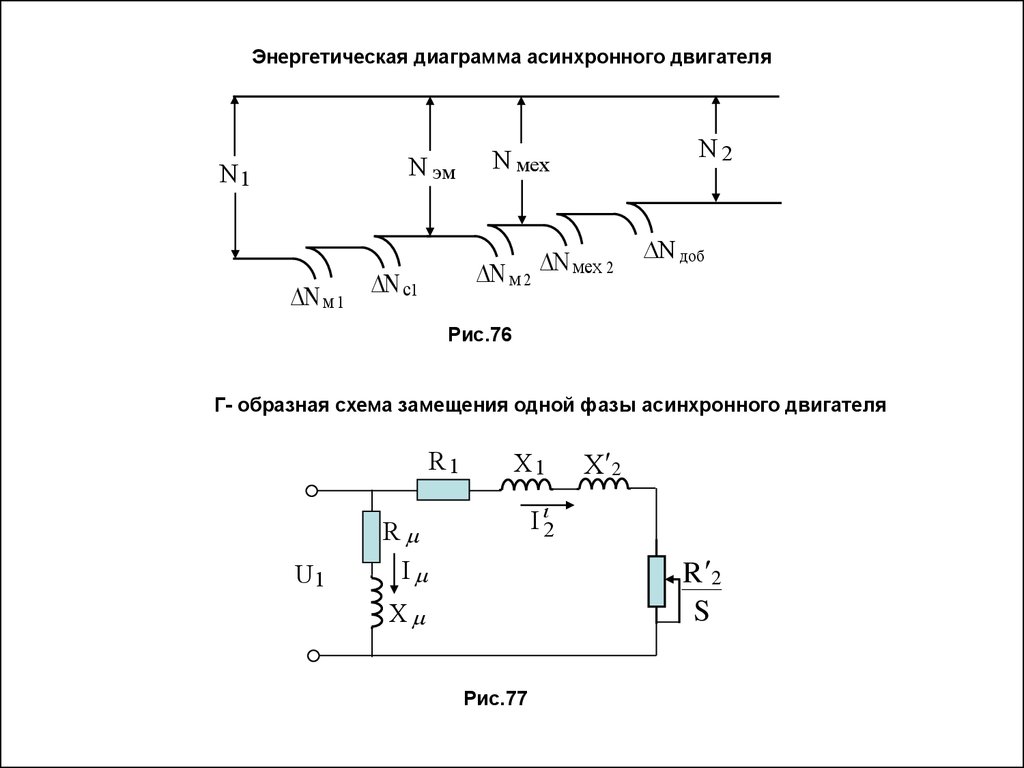

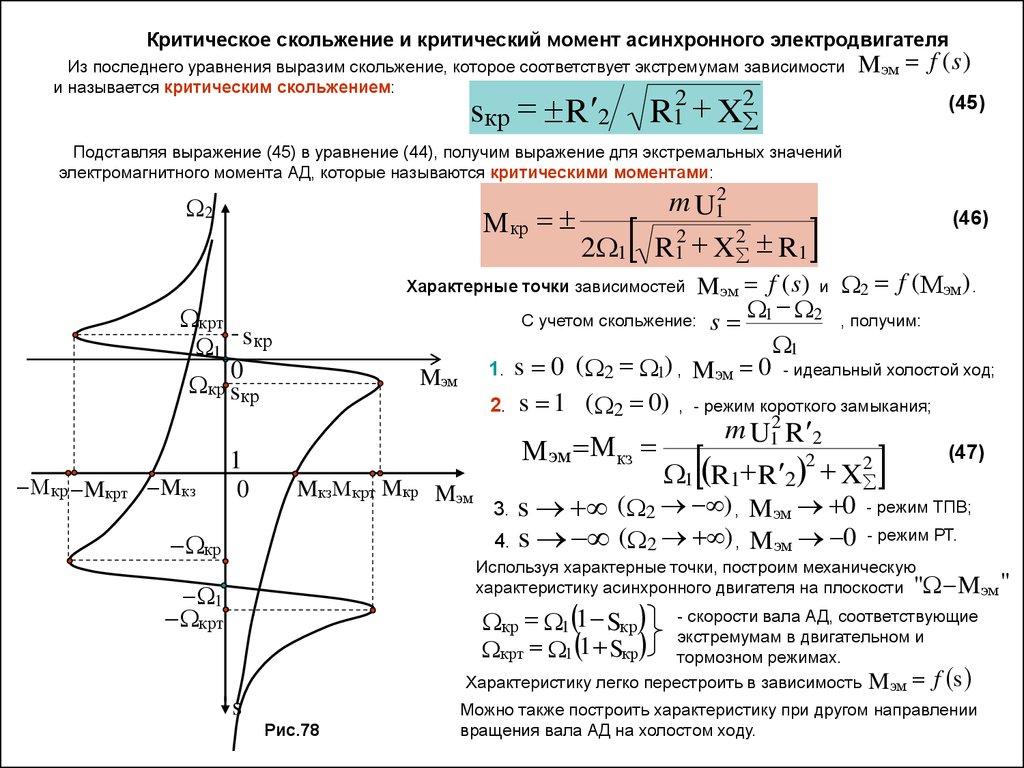


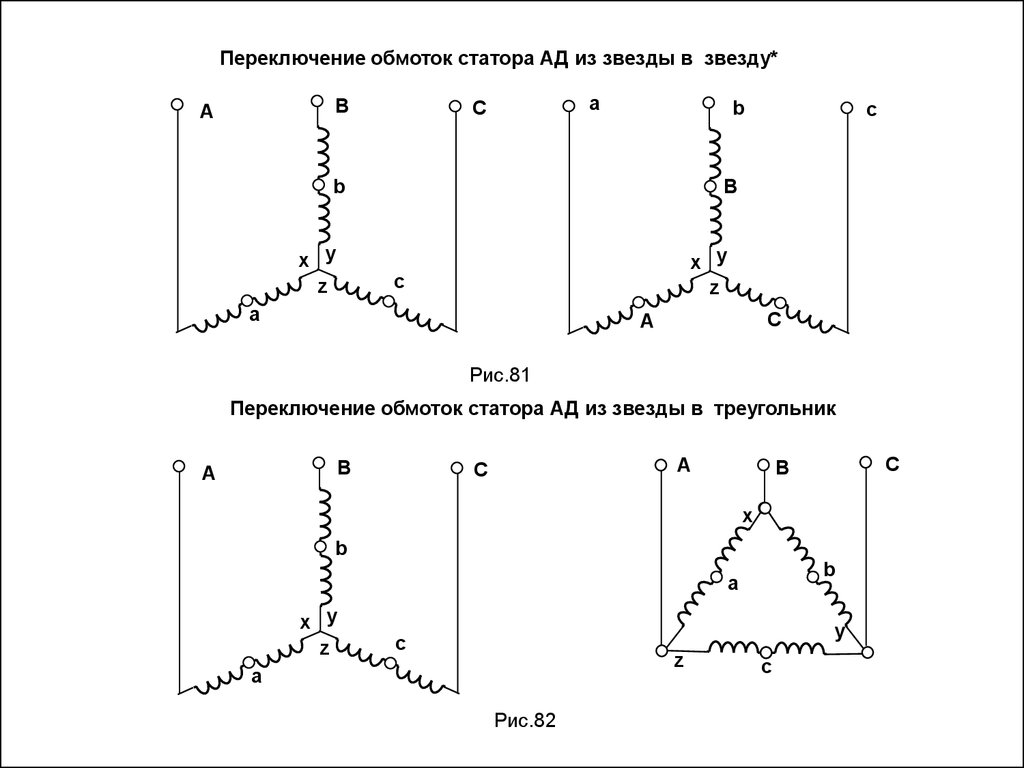




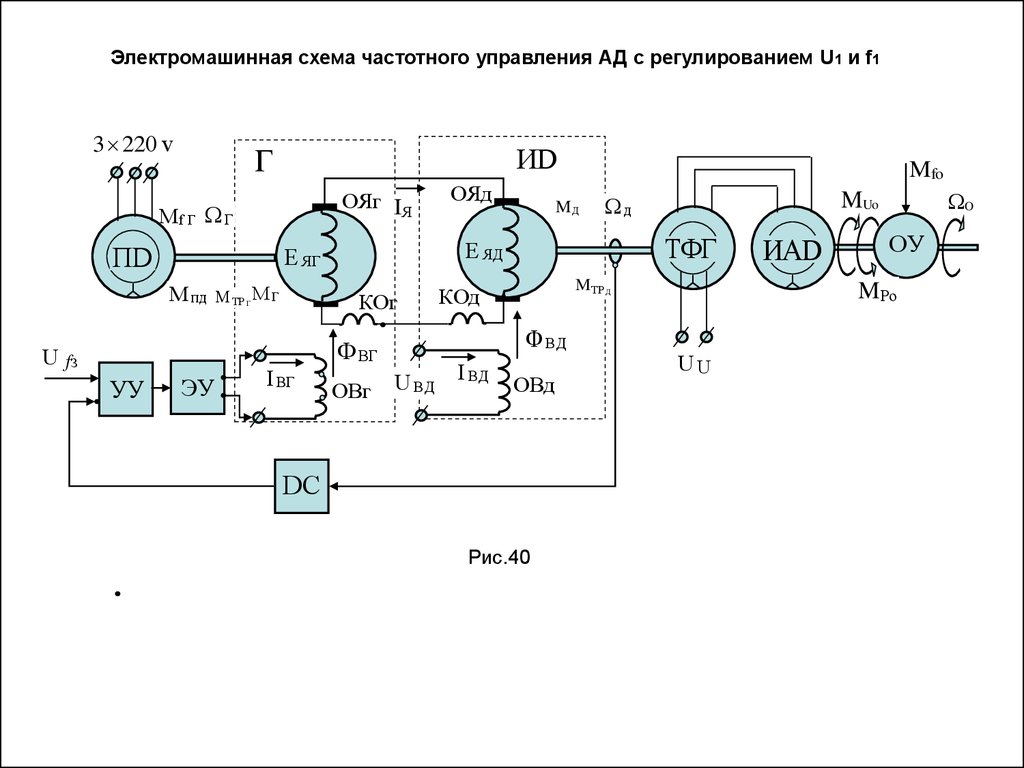









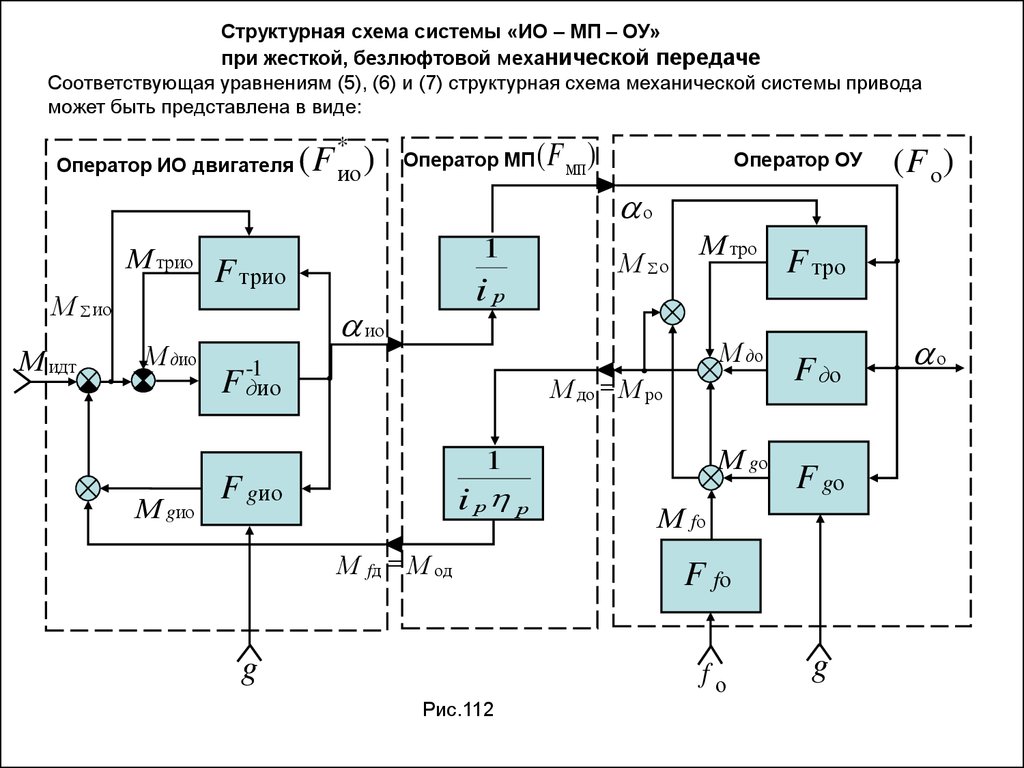


 Электроника
Электроника








