Похожие презентации:
Planowanie tras z wykorzystaniem narzędzia Solver
1. Planowanie tras z wykorzystaniem narzędzia Solver
Problem KomiwojażeraWykonali:
Wioletta Serwecińska
Angelika Marków
Nazarii Utynkevych
Krystian Wulw
2. Znaczenie słowa komiwojażer ?
• Wyobraźmy sobie akwizytora, który podróżuje od miasta do miasta,sprzedając swoje produkty lub zawierając różne oferty handlowe.
Wyrusza z miasta rodzinnego, po czym jego trasa przebiega dokładnie
jeden raz przez każde z miast. Na koniec komiwojażer powraca do
swojego miasta rodzinnego. Z oczywistych powodów chce, aby trasa
podróży była najkrótszą ze wszystkich możliwych tras. W ten sposób
powstaje problem wędrującego komiwojażera
3. Wprowadzenie
Podejmowanie decyzji we współczesnej organizacji jest procesemrozwiązywania złożonych problemów, z których dużą grupę stanowią
logistyczne zagadnienia optymalizacyjne. Zasada racjonalności działania
ekonomicznego wymaga od decydentów respektowania reguły, że
każda decyzja powinna spowodować maksymalizację korzyści. Obszary
optymalizacji procesów logistycznych rozwiązywalnych przy użyciu
metod z zakresu badań operacyjnych obejmują zagadnienia, wśród
których można wymienić:
4. Slajd 4
-problemy alokacji środków produkcji optymalny przydział surowców,zdolności produkcyjnej maszyn oraz dysponowanego czasu pracy ludzi
pomiędzy poszczególne wyroby (produkty), jakie może produkować
firma (kryterium optymalizacji: maksymalizacja zysku);
-zagadnienia transportowe optymalizacja przewozów towarów między
różnymi dostawcami i odbiorcami z uwzględnieniem punktów
przeładunkowych (kryterium optymalizacji : minimalizacja łącznego
kosztu przewozu towaru);
-problemy komiwojażera komiwojażer ma za zadanie odwiedzić
określoną liczbę klientów i wrócić do bazy tak, aby cała jego podróż
była jak najkrótsza (kryterium optymalizacji: minimalizacja długości
drogi w sieci łączącej wszystkie węzły);
5. Slajd 5
-zarządzanie zapasami surowców: gospodarka zapasami i obliczanieoptymalnej partii zapasów towarów, materiałów oraz wyliczenie zapasu
buforowego (kryterium optymalizacji: minimalizacja kosztów
działalności przedsiębiorstwa);
-zagadnienia wymiany ustalenie optymalnego momentu wymiany
pracującego środka trwałego na nowy (teoria odnowy) w
przedsiębiorstwie, wyważenie pomiędzy kosztami eksploatacji i
amortyzacji (kryterium optymalizacji: minimalizacja kosztów
działalności firmy);
-problemy przydziału zadań do wykonania w taki sposób, aby osiągnąć
np. najkrótszy łączny czas wykonania zadania (kryterium optymalizacji
minimalizacja czasu realizacji przedsięwzięć przy posiadanych
środkach).
6. Solver, jako narzędzie optymalizacji procesów logistycznych
Narzędzie Solver jest jednym z najbardziej zaawansowanychnarzędzi analitycznych MS Excel i jednocześnie jednym z prostszych w
obsłudze. Można z niego korzystać po jednokrotnym zainstalowaniu.
Solver wykorzystywany jest do rozwiązywania jednokryterialnych
zadań optymalizacyjnych, w których liczba zmiennych decyzyjnych nie
przekracza 200. Jego zastosowanie wymaga zapisania modelu
matematycznego w obszarze roboczym arkusza kalkulacyjnego. Model
optymalizacji składa się z trzech elementów:
7. Slajd 7
komórki celu (funkcja celu) - jest to komórka w modelu arkusza,która w wyniku zastosowania Solvera ma przyjąć wartość minimalną,
maksymalną lub ustaloną w postaci liczby rzeczywistej;
komórek zmiennych (zmienne decyzyjne) są one komórkami
zawierającymi poszukiwane wartości, które są zmieniane iteracyjnie i
podstawiane przez dodatek Solver do funkcji celu, dopóki nie zostanie
znalezione rozwiązanie optymalne;
komórek ograniczeń (mogą być zastosowane w stosunku do wartości
komórki celu i komórek zmienianych) wprowadzone warunki
ograniczające stanowią formułę w komórce arkusza, której wartość
musi mieścić się w określonych granicach lub osiągać wartości
docelowe.
8. Propozycja rozwiązania problemu wyboru tras
Zagadnienie rozpatrywane na potrzeby firmy kurierskiej należy doproblemów optymalizacyjnych, a do jego rozwiązania należy
zastosować tzw. Problem komiwojażera. Rozwiązanie problemu
komiwojażera dotyczy wyznaczenia najkrótszej trasy przejazdu
pomiędzy pewną liczbą punktów w taki sposób, aby każdy punkt został
odwiedzony przez kierowcę tylko jeden raz. Problem komiwojażera
związany jest z tzw. cyklem Hamiltona w grafie, tzn. takim cyklem, w
którym każdy z wierzchołków danego grafu wystąpi dokładnie jeden
raz.
9. Cykl Hamiltona
• Znalezienie właściwego cykluHamiltona jest zadaniem bardzo
trudnym obliczeniowo.
Wyobraźmy sobie graf
zupełny (ang. Complete graph graf, w którym każdy wierzchołek
jest połączony z każdym) o 10
wierzchołkach.
10. Ile różnych cykli Hamilton zawiera taki graf?
Otóż pierwszą krawędź cyklu można wybrać na 9 różnych sposobów,ponieważ każdy wierzchołek grafu jest połączony krawędzią z pozostałymi
dziewięcioma. Po wyborze pierwszej krawędzi pozostaje nam 8 możliwych
wyborów, później 7, 6 5 ... 1. W efekcie otrzymujemy liczbę cykli Hamiltona
równą:
• LH = 9 • 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1 = 9! = 362880
Dla n wierzchołków:
• LH = (n - 1) • (n - 2) • ... • 3 • 2 • 1 = (n - 1)!
11. Slajd 11
Wynik jest bardzo niekorzystny, ponieważ prowadzi do wykładniczejklasy złożoności obliczeniowej O(n!). Dla każdego znalezionego cyklu
Hamiltona liczymy sumę wag krawędzi i zapamiętujemy cykl o
najmniejszej sumie wag. Na przykład w naszym grafie może to być
następujący cykl (nie sugeruj się długością krawędzi na rysunku - ważne
są wagi, a nie długość kreski - czasami miasta mało odległe w linii
prostej mogą być połączone długą trasą ze względu na warunki
terenowe: góry, jeziora, bagna itp.):
12. Slajd 12
• Grafy odwzorowujące rzeczywistesieci połączeń zwykle nie są
zupełne - ekonomicznie
nieuzasadnione byłoby budowanie
osobnych dróg pomiędzy każdą
parą miast. Zwykle drogi
przebiegają od jednego miasta do
drugiego, a w niektórych się
rozchodzą. Dlatego opisany
powyżej przypadek jest
przypadkiem pesymistycznym.
Jednakże problem dalej posiada
wykładniczą klasę złożoności
obliczeniowej. Rozważmy dla
przykładu graf posiadający 100
wierzchołków.
13. Slajd 13
• Załóżmy, iż każdy wierzchołek łączy się z czterema innymi wierzchołkami grafu.Zatem ich stopień wynosi 4. W pesymistycznym przypadku ilość cykli Hamiltona
do przebadania może wynosić:
pierwszego wierzchołka możemy pójść na 4 różne sposoby, z drugiego na 3, z
trzeciego na 3, ..., i z 99 na trzy. Otrzymujemy zatem:
• LH = 4 • 399 ≈ 3100 ≈ 5,15 • 1047
Zatem dla grafu posiadającego n wierzchołków o stopniu s otrzymamy
LH ≈ (s - 1)n
Czyli liczba cykli lub ścieżek do przebadania rośnie wykładniczo. Nawet na szybkim
komputerze wyznaczenie rozwiązania może przekroczyć stulecia. Problemy
algorytmiczne o złożoności wykładniczej są traktowane jako nierozwiązywalne dla
dużych n.
14. Slajd 14
• Istnieją algorytmy znajdujące przybliżone rozwiązania problemuwędrującego komiwojażera w czasie wielomianowym, lecz są one
bardzo zaawansowane i trudne w implementacji. Jeśli liczba
wierzchołków w grafie nie jest duża (np. do 20) i graf nie jest grafem
zupełnym (złożoność O(n!)), to rozwiązanie problemu komiwojażera
możemy uzyskać prostym algorytmem, który wyznacza wszystkie
cykle Hamiltona, liczy sumę wag krawędzi i zwraca cykl o najmniejszej
sumie wag. Rozwiązanie to jest o tyle dobre, iż zawsze zwróci cykl
optymalny, a nie przybliżony. Również jest łatwe do zrozumienia i
implementacji. Podstawowa wada to wykładnicza złożoność
obliczeniowa, która uniemożliwia analizę większych grafów.
15. Przykład
W prezentowanym przypadku kurier musi dotrzeć do 9 miast i na koniec dojechać do bazyw Gdyni. Należy wyznaczyć, zatem taką trasę (rysunek 1), aby całkowita długość drogi do
przejechania była jak najmniejsza (aby zminimalizować koszty transportu i jednocześnie
osiągnąć najkrótszy czas pracy kierowcy). Znalezienie właściwego cyklu Hamiltona jest
zadaniem trudnym obliczeniowo. ponieważ w grafie pełnym składają cym się z 10
wierzchołków, liczba cykli Hamiltona wynosi 9!,czyli 362 880.
Gdyby kurier miał do odwiedzenia jeszcze tylko jedną dodatkową miejscowość, niż w
prezentowanym przypadku to liczba ta wzrosłaby do3 628 800.
W przypadku 25 miejscowości to aż 15 511 210 043 330 985 984 000 000 różnych
wariantów wybrania kolejnych lokalizacji podczas realizacji zadania. Obrazuje to wyraźnie
jak wiele możliwości uszeregowania tras można zaproponować i wskazuje dobitnie, że
realizacja tego zadania dotychczasową metodą (bez wsparcia informatycznego) byłaby nie
tylko trudna i czasochłonna, ale czasami wręcz niemożliwa. Dodatkowo nie dawałaby też
pewności, co do wybrania optymalnego rozwiązania z punktu widzenia założonych
kryteriów.
16. Slajd 16
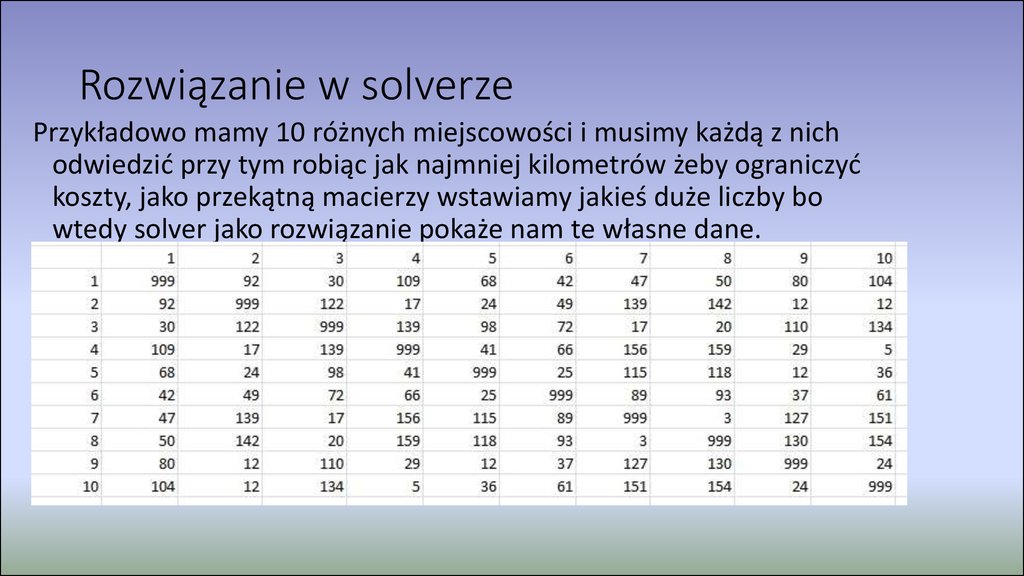
17. Rozwiązanie w solverze
Przykładowo mamy 10 różnych miejscowości i musimy każdą z nichodwiedzić przy tym robiąc jak najmniej kilometrów żeby ograniczyć
koszty, jako przekątną macierzy wstawiamy jakieś duże liczby bo
wtedy solver jako rozwiązanie pokaże nam te własne dane.
18. Slajd 18
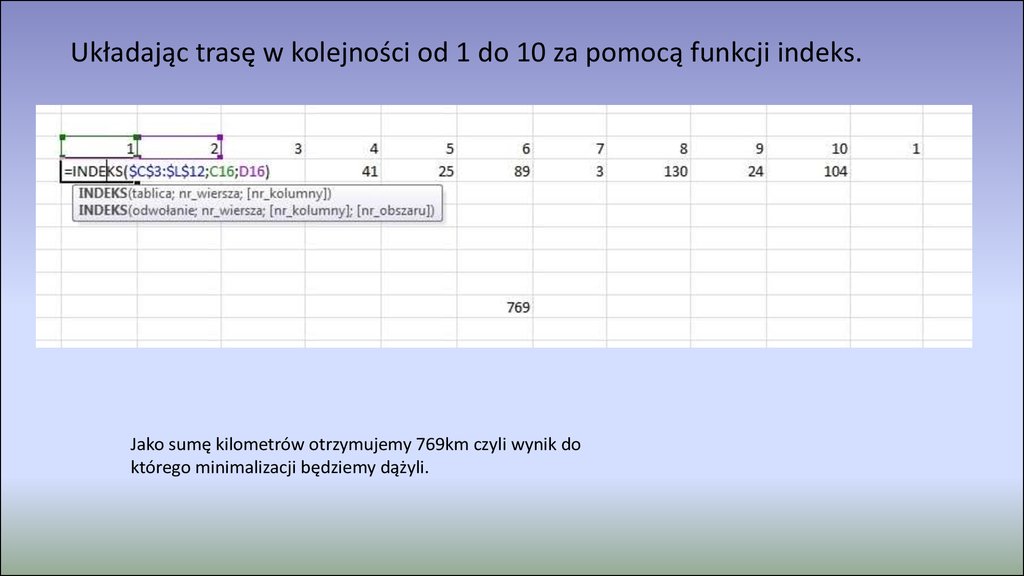
Układając trasę w kolejności od 1 do 10 za pomocą funkcji indeks.Jako sumę kilometrów otrzymujemy 769km czyli wynik do
którego minimalizacji będziemy dążyli.
19. Slajd 19
20. Slajd 20
21. Slajd 21
Jedynym warunkiem jaki przyjmujemy jest, że komórki które aktualnieprzyjmują wartości od 1-10 muszą być różne czyli wybieramy warunek
DIF czyli AllDifferent czyli każda z liczb musi być różna od siebie. A jako
metodę wybieramy Evolutionary i dajemy Solve.
22. Slajd 22
Wynik wyszedł 318km, przypomnijmy poprzedni przy trasie od 1-10 to769km a to jest 2,41 razy trasy mniej a więc nasz Salesman zaoszczędzi
dosyć sporo na tej trasie. Solverowi zajmuje to około kilkudziesięciu
sekund a musi rozparzyć 9! możliwości czyli 362 880 więc człowiekowi z
kalkulatorem i kartką zajęło by to prawdopodobnie więcej czasu niż
przejechanie tej całej trasy





















 Промышленность
Промышленность


