Похожие презентации:
Тема 6. Магнитные возбуждения в твердом теле. Магнетизм
1.
Тема 6.Магнитные возбуждения в твердом
теле
2.
Магнетизм – взаимодействие междудвижущимися зарядами
Взаимодействие осуществляется магнитным полем
Источник магнитного поля - движение зарядов
Количественная характеристика магнитного поля –
его напряженность H
J
dH 3 ds R
cR
J
H
c
J
dF ds H
c
Для замкнутых токов
ds R
R3
J
F
c
ds
H
3.
Магнетизм атомовСпособность атомов взаимодействовать с магнитным
полем характеризуется магнитным моментом M
Для замкнутого контура с током M I S n
Магнитный момент атома обусловлен
микроскопическими токами, создаваемыми :
1) орбитальным движением электронов
2) спинами электронов и ядер
4.
Одноэлектронные атомыОрбитальный момент импульса электрона : Pel l (l 1)
Проекция момента на произвольную ось z : Pelz ml
Проекции на другие оси не определены
Pely Pelx
Орбитальный магнитный момент электрона :
M el g el Pel l (l 1) B
e
g el
2m
e
B
2m
Магнитомеханическое отношение
Проекция магнитного момента на произвольную ось z :
M elz ml B
5.
Одноэлектронные атомыСпин электрона :
1
s
2
Pes s(s 1) ,
Проекция спина на произвольную ось z :
Psz ms ,
1
ms
2
Psx Psy
Спиновый магнитный момент электрона :
M es
e
g es Pes s(s 1)
3 B
m
Магнитомеханическое отношение
e
g es
m
Проекция магнитного момента на произвольную ось z :
M esz B
6.
Одноэлектронные атомыСпин-орбитальное взаимодействие
Pa Pel Pes
Полный момент импульса электрона и его проекция
Pa j ( j 1)
Paz m j
j l s , m j ml ms
Полный электронный магнитный момент атома :
1 e
Ma
2m
j ( j 1)
j ( j 1) B
Поправки к энергии – тонкая структура уровней
me4
e4
n
3
En 2 2 [1 2 2 {
}]
2 n
n j 1 4
2
7.
Магнетизм многоэлектронных атомовМногоэлектронный атом можно рассматривать в приближении
самосогласованного центрально-симметричного электрического поля.
Квантовое состояние определяется электронной
конфигурацией т.е. числом электронов с заданными l и n
Все состояния c данным n –составляют электронную
оболочку. Замкнутая оболочка – электронный слой
Мах число таких состояний 2(2 l +1)
например 1p 6 эквивалентных сост.
Заполнение оболочек e
K 1s2
2 электрона
L 2s2, 2p6
8 электронов
M 3s2, 3p6, 3d10
18 электронов
N 4s2, 4p6 4d10, 4f14 32 электрона
nl
2 ( 2 l 1)
Уровни энергии в сложный атомах обозначают
большими буквами латинского алфавита
8.
Многоэлектронные атомыПолный орбитальный момент атома
Z
PaL Peli L( L 1)
i 1
PaLz mL
Z
L li
i 1
Полный магнитный орбитальный момент атома
M aL L( L 1) B
Полный спиновый момент атома
Z
PaS Pes i S ( S 1)
i 1
PaSz mS
Z
S m si
i 1
Полный спиновый магнитный орбитальный момент атома
M aS 2 S ( S 1) B
9.
Многоэлектронные атомыПолный момент атома
Pa PeL PeS
Pa J ( J 1)
Его проекция Paz m J mJ 0, 1.... J
Тяжелые атомы: J-J связь
Z
Pe Pel Pes Pa Pei
i 1
M a M aL M aS
Ma не антипараллелен
Pa
M aS
M aL
2
PaS
PaL
J L S
Спин-орбита
10.
Проекция магнитного момента, нанаправление механического момента
M aP M aL cos( PaL Pa ) M aS cos( PaS Pa )
M aP M aL cos( ) M aS cos( )
Из геометрических соображений:
S ( S 1) J ( J 1) L( L 1)
cos( )
2 S ( S 1) J ( J 1)
L( L 1) J ( J 1) S ( S 1)
cos( )
2 L( L 1) J ( J 1)
J ( J 1) S ( S 1) L( L 1)
M aP [1
] J ( J 1) B
2 J ( J 1)
11.
Многоэлектронные атомыM aP g J J ( J 1) B
J ( J 1) S (S 1) L( L 1)
gJ 1
2 J ( J 1)
g J 1 для S 0 g J 2 для L 0 Фактор Ланде
Проекция магнитного момента на внешнее магнитное поле
M aPz g J mJ B
mJ 0, 1.... J
Эффективный магнитный момент атома
(M aPz ) max g J J B
12.
Магнитные моменты атомных ядерАналогия протона с электроном не проходит !!!
M p 2,79 яB
яB
M n 1,9 яB
e
Ядерный магнетон Бора
2m p
яB B
Спин ядра Pя I ( I 1)
I 0, 1 / 2 , 1, 3 / 2 , 2 , ......
Магнитный момент ядра
Mя Mni Mpi
M я g я I ( I 1) яB
Проекция магнитного
момента ядра
M яZ g я mI яB
mI 0, 1/ 2 , ...... I
13.
Основы теории магнетизма т.т.Все тв.тела. в магнитом поле H – приобретают магнитный
момент, т.е. намагничиваются
Вектор намагниченности Im - магнитный момент ед. объема
M
Im
Hi
V
Направление I
Im H
Im H
Напряженность поля внутри магнетика - индукция
B H Hi Im H
Магнитная
восприимчивость
B H H (1 ) H
1
Магнитная проницаемость
14.
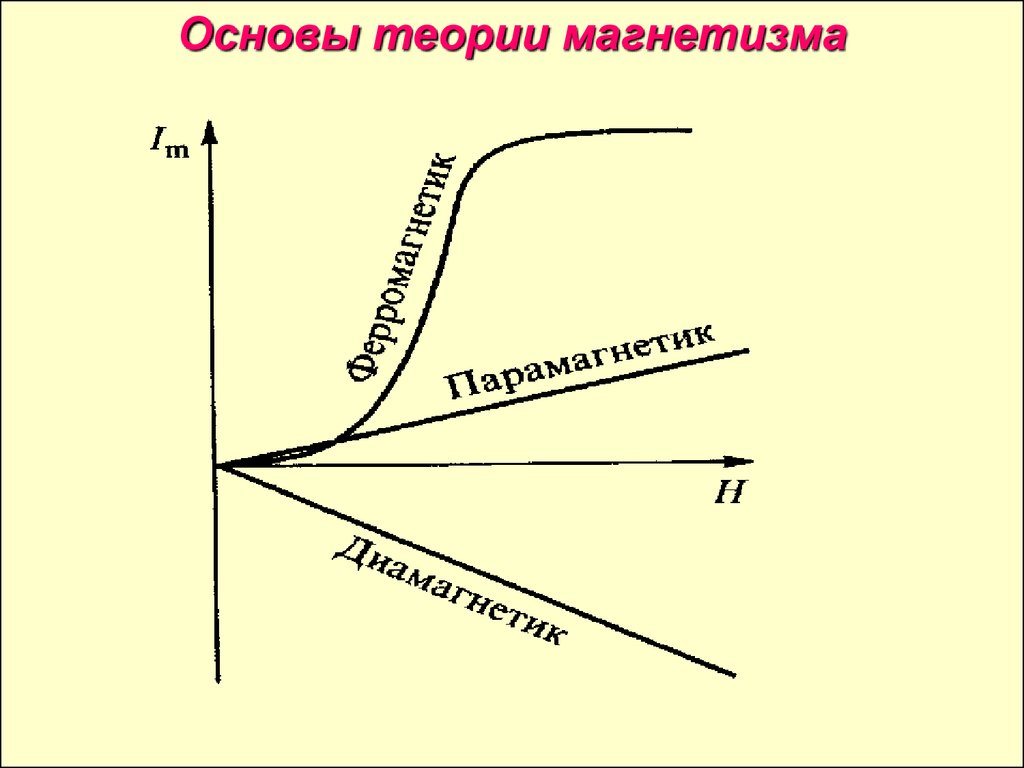
феноменологияПо магнитным свойствам все вещества делятся на:
Диамагнетики <0 и не зависит от T и H ( < 1)
Парамагнетики >0 не зависит H, зависит от T ( > 1)
Ферромагнетики >>0 и зависит от H :
ферромагнетики,
антиферромагнетики
ферримагнетики
Причины – Изменение магнитного момента атомов
во внешнем магнитном поле,
Взаимодействие магнитных моментов атомов
15.
Основы теории магнетизма16.
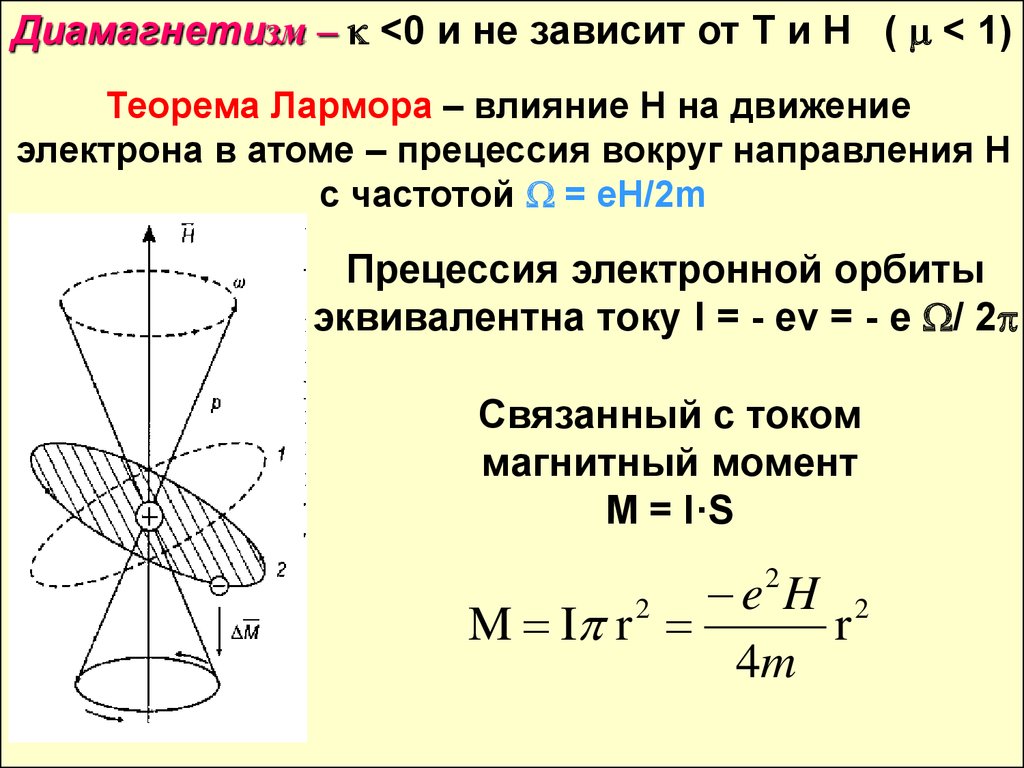
Диамагнетизм – <0 и не зависит от T и H ( < 1)Теорема Лармора – влияние H на движение
электрона в атоме – прецессия вокруг направления Н
с частотой = eH/2m
Прецессия электронной орбиты
эквивалентна току I = - ev = - e / 2
Связанный с током
магнитный момент
M = I·S
e H 2
M I r
r
4m
2
2
17.
В атоме содержащем Z электроновсуммарный ток I = (- eZ) / 2 = -Ze2H/4 m
M I r
2
s
e HZ 2
rs
4m
2
Для тв.тела. с N атомов на ед. объема:
2
MN 1
e ZN 2
rs
V H
4m
2
s
r
2 2
r
3
Диамагнетизм есть всегда, но проявляется в
атомах с нулевым собственным
магнитным моментом
18.
Парамагнетизм >0 не зависит H, зависит от T ( >1)
Имеет место в т.т. состоящих из атомов с
ненулевым собственным магнитным моментом
В отсутствие внешнего H моменты атомов
распределены случайно и <Ma>=0
В магнитном поле моменты стремятся
ориентироваться по полю
Энергия момента, отклоненного от поля на угол :
Wm= -Ma·H·cos( )
W min при = 0
Тепловое движение наоборот, разупорядочивает моменты
Надо найти среднее значение < MaH>
под действием поля и температуры
19.
Вероятность того, что момент ориентированпод углом + d к магнитному полю
= C ·exp(Ma·H·cos( )/kT)sin( )
d
Среднее значение проекции момента на
направление H
MH Ma
M a H cos( )
) sin( )d
0 cos( ) exp(
kT
M a H cos( )
) sin( )d
0 exp(
kT
20.
ПарамагнетикиMaH
kT
MH Ma[cth(
)
]
kT
MaH
Для <<1
M aH
kT
1
MH Ma[cth( ) ]
cth( ) - 1/ = /3
Для N атомов намагниченность Im равна N·MH
2
a
NM H
1
I m NMa
3
3kT
= Im/H
= N·Ma2
/3kT
Закон Кюри =С/T
Закон Кюри - Вейса =С/(T- )
=С/T
C = N·Ma2 /3k –
постоянная Кюри
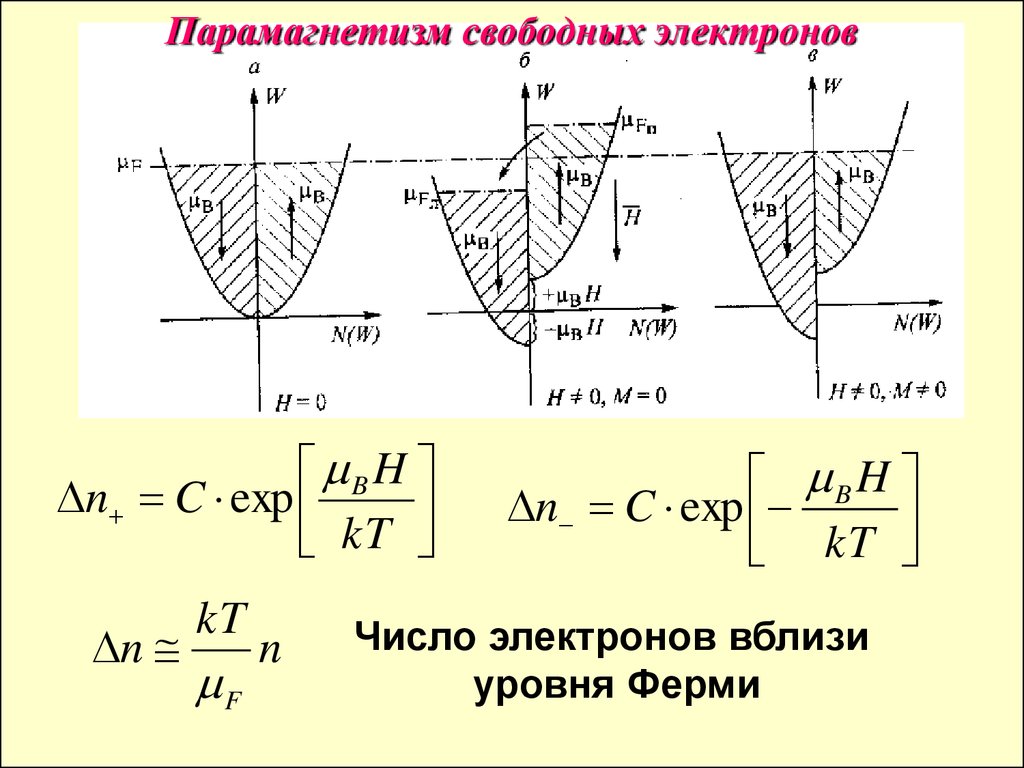
21.
Парамагнетизм свободных электроновB H
n C exp
kT
n
kT
F
n
B H
n C exp
kT
Число электронов вблизи
уровня Ферми
22.
MB ( n n )
n n n
V
B H
B H
I m C B exp
exp
kT
kT
B H
B H
n C exp
exp
kT
kT
n
C
B H
B H
exp
exp
kT
kT
B H
kT
exp exp
I m n B
n B th
exp exp
23.
1th
I m n B th
n B H
2
kT
I m n B
e
H
kT
n
2
kT
F
n
n B
2
e
F
Магнитная восприимчивость e не зависит от Т
24.
Ферромагнетики>>0 и зависит от H
Домены - области спонтанной намагниченности
параллельная ориентация магнитных моментов
Источники образования доменов:
Не скомпенсированный спин электронных оболочек
Обменное взаимодействие электронов
Электростатическая природа!!!!
25.
Тождественность частицв.ф. системы, получающиеся при перестановке пары
одинаковых частиц отличаются множителем exp(i ),
Двойная перестановка
exp( 2i ) exp( i ) 1
Для систем с S=n/2 В.Ф. Антисимметрична Меняет знак при при нечетном числе перестановок
Для систем с S=n В.Ф. Симметрична –
Не меняет знак при любом числе перестановок
26.
Принцип ПаулиВ.ф. Системы двух невзаимодействующих электронов
I(1,2) = (1)· (2)
I I(1,2) = (2)· (1)
= c1· I + c2· I I в.ф. Антисимметрична т.е. c1=- c2
анти(1,2) = [1/ 2] ·[ (1)· (2)- (2)· (1)]
Если электроны в одном состоянии то
= анти(1,2) 0
27.
Обменное взаимодействие2
e
Uˆ
r12
(1,2) (r1 , r2 ) S (sz1, sz2 )
(1,2)
(2,1)
1
(r1 ) (r2 ) (r2 ) (r1 )
(r1 , r2 )
r1 r2 и sz1 sz2
2
U Uˆ dv1dv2
*
Введем обозначения:
dv1 dx1dy1dz1
dv2 dx2 dy2 dz2
(r1 ) e (r1 ) , (r1 ) e (r1 ) (r1 )
2
2
*
(r2 ) e (r2 ) , (r2 ) e (r2 ) (r2 )
*
*
28.
Обменное взаимодействие(r1 ) (r2 )
(r1 ) (r2 )
U
dv1dv2
dv1dv2
r12
r12
*
(r1 ); (r1 )
Плотность «размазанного» заряда
(r1 ) (r2 )
2
e
Вероятность нахождения частиц
в одной и той же точке
пространства
*
29.
Обменное взаимодействиеW= - 2I(S1,S2)
2
2
2
2
e e e
e
I ( )ψa (1)ψa (2)ψ b (1)ψ b (2)dV1dV2
rab r12 r1b r2 a
30.
31.
ФерримагнетикиНеравенство магнитных моментов атомов
в различных подрешетках
парамагнетик
ферромагнетик
антиферромагнетик
ферримагнетик
32.
Доменая структурастенка Блоха
33.
Спиновые волныОтклонение спина, распространяющееся в пространстве
Wo = -2I·N·S2
m= 4·I·S·(1- cos(ka))
ka<<1 1- cos(ka) = 0.5·(ka)2
nmk
NU
2S
2
k
m= 2I·S·(ka)2
WM nmk m































 Физика
Физика








